バブルシューターゲームのレシピ

前言

バブルシューターゲームは結構古いパズルゲームの一種です。
このジャンルの元祖は確かに1994年にリリースされたパズルボブルというゲームです。
最近私は趣味でこのジャンルの基本的なゲームプレイを実装してみましたので、ここで実装に当たって解決しなければいけない課題及び自分の解決策を共有しようと思っています。

一応ここで説明するのはこのようなゲームを組み込むに必要となる知識のみなので、ゼロから完成までのステップ・バイ・ステップ的な手順書ではありません。
それぞれの課題を突破する方法はきっとここで説明するもの以外も沢山あると思いますので、ご参考まで。

バブルシューターゲームとは＆実装の課題

まず、バブルシュータゲームとは一体どんなタイプのゲームでしょうか。
簡単に言うと、バブルを一つずつ発射し、以下のルールに従って既存のバブルを全部消すゲームです。
1. 発射されたバブルが天井にぶつかったら天井に付けます。
2. 両側の壁にぶつかったら反射されます。
3. 既存バブルにぶつかって、同じ色のバブルがこのバブルによって三つ以上繋がっているようになったら、このバブルに繋がっている同じ色のバブルを全部消します。
4. そうでもない場合はぶつかったバブルに付けます。
5. 直接もしくは間接に天井に繋がっていないバブルは全部落下します。
6. もし直接もしくは間接に天井に繋がっているバブルが一定の低さに到達したら、プレイヤーが負けます。

イメージ的には以下のような感じです。

では、基本的なゲームプレイを作るにはどんな問題を解決しなければいけないでしょうか？
1. マップを表示するデータストラクチャ。ご覧通り、バブルを密着に表現するため、マップは普通な長方形ではなく、隣接する行がちょっとずれていて、バブルが周り六つのバブルと隣接しています。
2. 発射されたバブルの衝突検知。つまり、そのバブルの周りに他のバブルまたは壁があるかどうかのことです。
3. 特定な条件を満たしていて、かつ、繋がっているバブルを探す方法。これさえ解決出来たら、繋がっている同じ色のバブルの探しや天井に繋がっていないバブルの検知も可能となります。

データストラクチャ

はじめに、最も基本的な課題はこのバブルが密着しているマップをうまく表示することです。
一バブルの周りに六つバブルがあることは、つまり、マップが六角形のセルで構成されていることです。

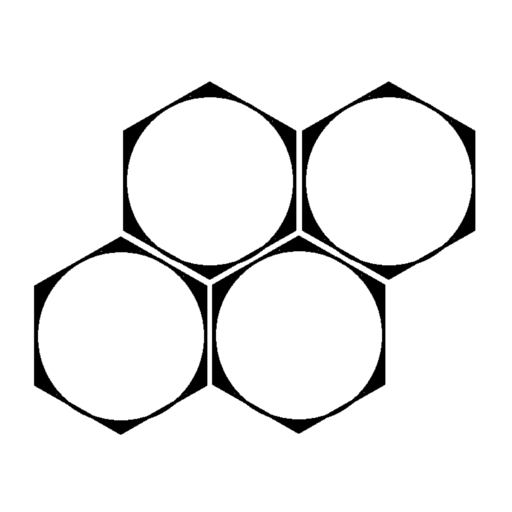
これで、問題は”どんなデータストラクチャを使ってこの六角形グリッドを表示する”に変換されました。
もちろん、カスタムのクラスを書いて隣接しているセルのレファレンスを持つ形でこのグリッドを表示することも出来ますが、
もっと効率がいい方法もあります。
グリッドをよく見ると、もし行毎のセル数が固定にすれば、実際、このグリッドは奇数行または偶数行をせべて右へ半セルぐらいの距離でシフトした配列として考えられます。

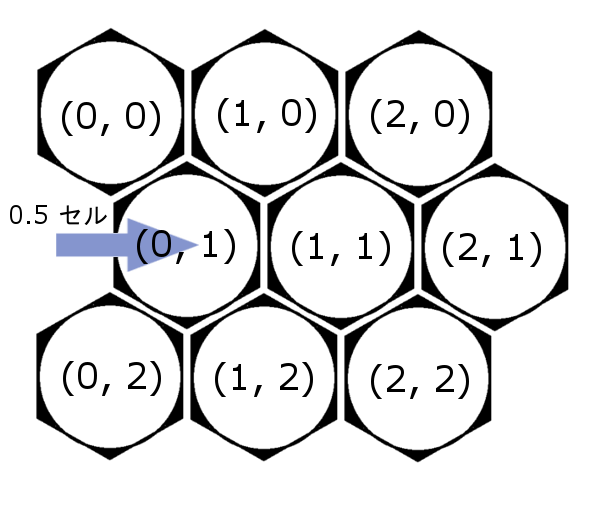
インデックスはそのままで、ただ画面上に表示する際、奇数行もしくは偶数行のセルを0.5セルずらすだけです。

function offsetToScreen(col, row, width, height) {
    var x = width * (col + 0.5 * (row % 2));
    var y = height * row;

    return new Point(x, y);
}

バブルが丸なので、それを外接する六角形は正六角形になります。
つまり、六角形の中心と各頂点で構成する六つの三角形が全部正三角形です。

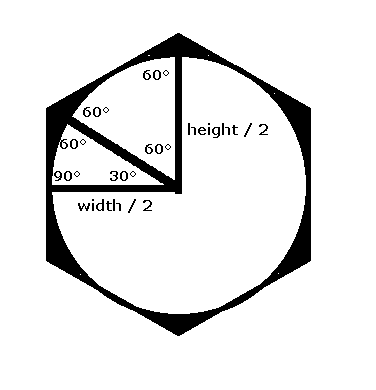
なので

width = height * cos(30°)

特定なセルの周りにあるセルをアクセスするのも簡単です。セルのインデックスを偏移することで出来ます。
隣接するセルのインデックス偏移値は偶数行と奇数行と違いますが、同じ偶数行・奇数行であればどのセルでも隣接セルとのインデックス偏移値が一緒です。

var NEIGHBOUR_GRID_OFFSETS_FOR_EVEN_ROW = [
    new Point(-1, 0), new Point(-1, -1), new Point(0, -1),
    new Point(1, 0), new Point(0, 1), new Point(-1, 1)
];

var NEIGHBOUR_GRID_OFFSETS_FOR_ODD_ROW = [
    new Point(-1, 0), new Point(0, -1), new Point(1, -1),
    new Point(1, 0), new Point(1, 1), new Point(0, 1)
];

座標系

次の課題を話す前に、まずこれから必要となる座標系のことについて少し説明しましょう。
今まで説明に使われているのはグリッドの行列インデックスを使う、一番直観的な座標系です。所謂偏移座標系です。

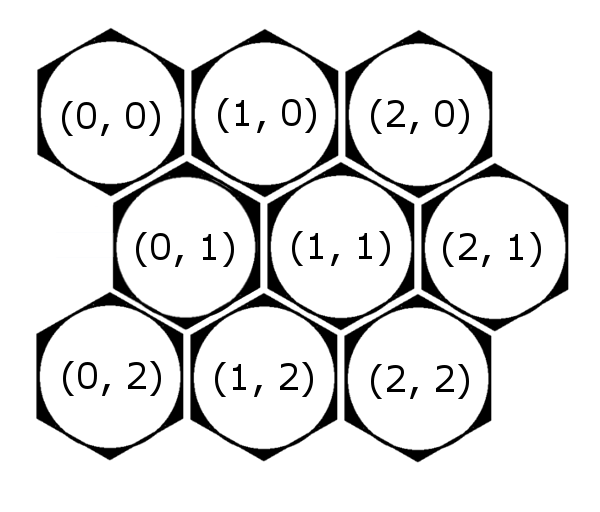
しかし、一番直観的なものが一番計算に便利だとは限りません。
六角形グリッドに関する計算にもっと適した座標系は以下のようなキューブ座標系です。

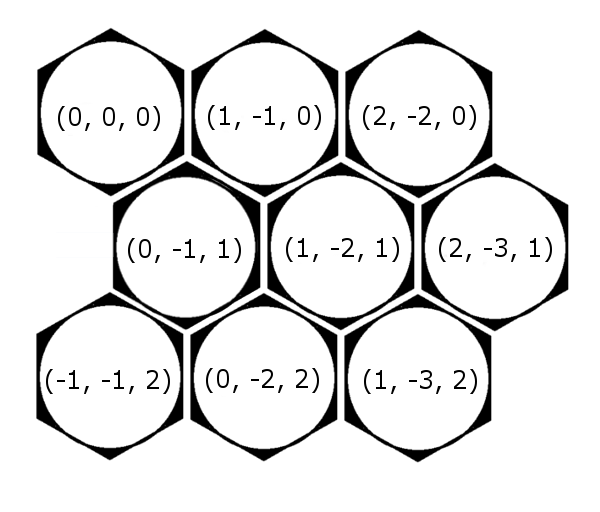
一見、”この三つの数字それぞれ何を指しているんだろう”と分かりにくいかもしれませんが、でも下図のようにx + y + z = 0平面のノーマル方向からキューブをみてください。

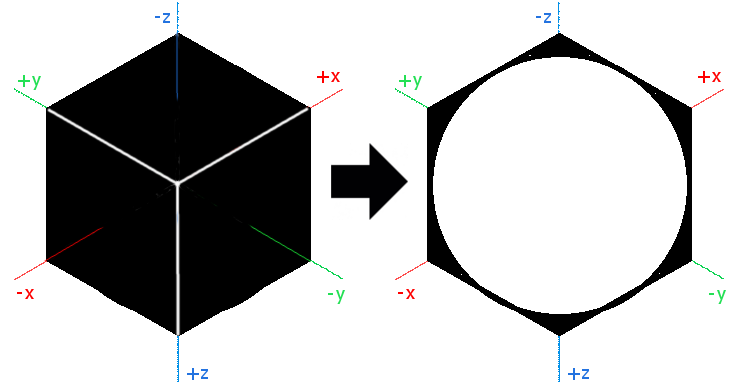
どうでしょう？正六角形になりましたよね？
更に面白いのは、キューブのx軸、y軸とz軸がちょうど正六角形の対角線になっていて、キューブで先ほどのグリッドを並んでみると：

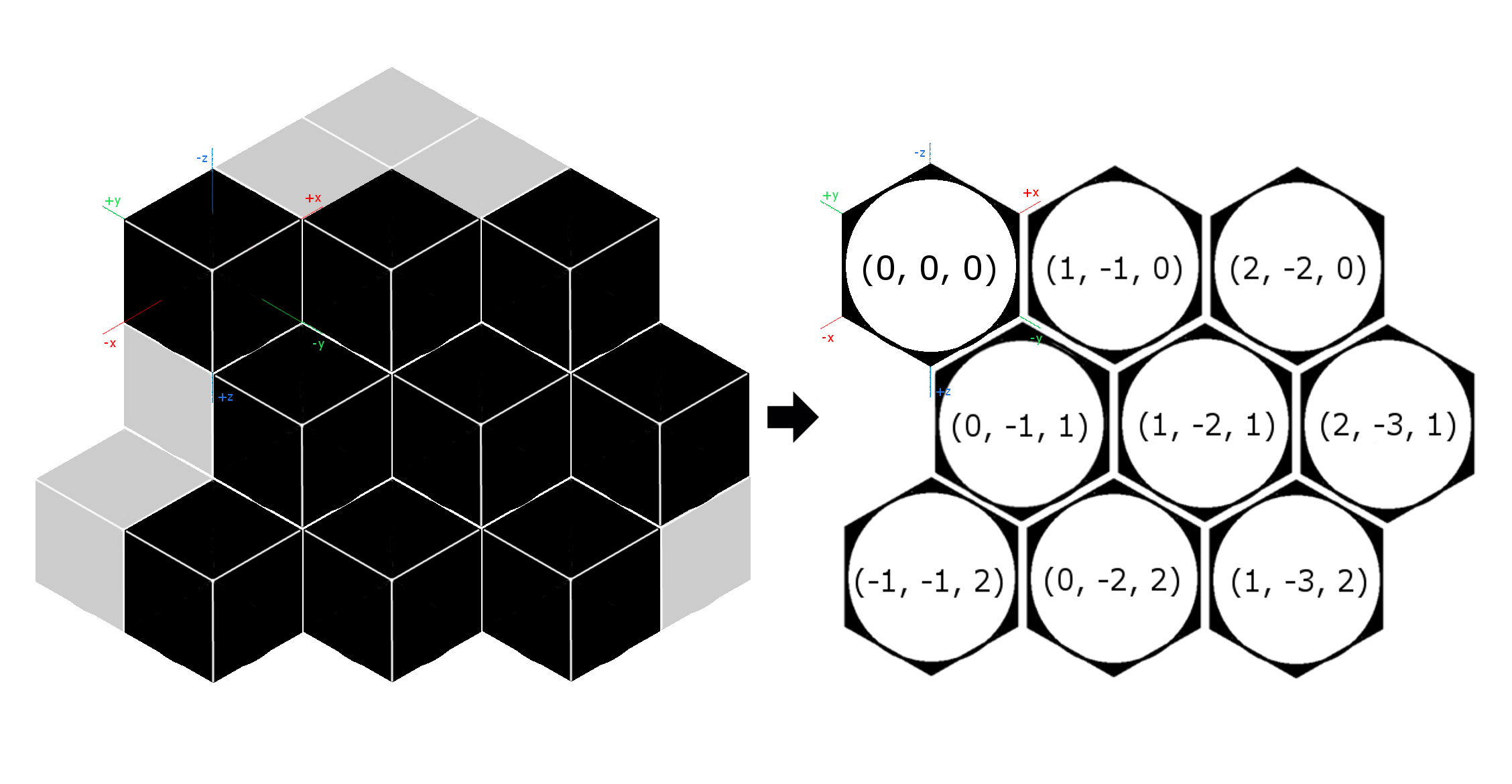
どうですか？ついさっきまた謎のようなその三つの数字の意味は少し分かるようになりましたか？
その三つ数字はまさに応じたキューブのx軸、y軸、z軸それぞれの座標です。
この故、このような座標系はキューブ座標系だと言われます。
キューブ座標系を使うメリットは色々ありまして、例えば、偶数行と奇数行を区分せずに色んな計算を行えること。
そのため、キューブ座標を使って画面位置を計算する時もこんな感じに出来ます：

function cubeToScreen(x, y, z, height) {
    var screenX = height / 2 * Math.sqrt(3) * (x + z / 2);
    var screenY = height * 3 / 4 * z;

    return new Point(screenX, screenY);
}

偏移座標とキューブ座標は以下のような感じで相互転換出来ます。

function offsetToCube(col, row) {
    var x = col - (row - row % 2) / 2;
    var z = row;

    // x + y + z = 0
    var y = 0 - x - z;

    return new Point(x, y, z);
}

function cubeToOffset(x, y, z) {
    var col = x + (z - z % 2) / 2;
    var row = z;

    return new Point(col, row);
}

衝突検知

データストラクチャを決めたら、次の課題はどうやって発射されたバブルが他のバブル・壁とぶつかっているかどうかを検知することです。
検知自体はそんなに難しいことではありませんが（バブルを格納するセルの周りのセルに何かあるを見るだけ）、ちょっと厄介なのは今バブルの画面上の位置から所属するセルを計算することです。
もしマップはレギュラー的な正方形グリッドだったら、簡単な除法計算で所属するセルを分かりますが、残念ながら、正六角形のグリッドには通用しません。
”offsetToScreenを逆にすればいいではないか”とも考えられるかもしれませんが、
その方法が適用出来るのは”偏移座標から画面位置へ変換する際に偏移座標の数値は整形であること”が前提ですから。
逆に画面位置から偏移座標へ変換すると、中心ではないポイントの偏移座標が小数部分を持つため、以下のようなケースが出ます。

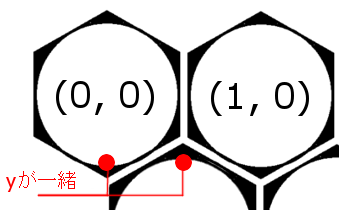
ここはキューブ座標系の出番です。
偏移座標と違って、キューブ座標であれば、例え小数部分が存在しても正しくラウンディング出来ます。
計算式はcubeToScreenを逆算する結果です。

function screenToCube(screenX, screenY, height) {
    var x = (screenX * Math.sqrt(3) / 3 - screenY / 3) / (height / 2);
    var z = screenY * 4 / 3 / height;
    var y = 0 - x - z;

    return cubeRound(x, y, z);
}

function cubeRound(x, y, z) {
    var rx = Math.round(x);
    var ry = Math.round(y);
    var rz = Math.round(z);

    var xDiff = Math.abs(rx - x);
    var yDiff = Math.abs(ry - y);
    var zDiff = Math.abs(rz - z);

    // x、y、zを全部ラウンディングしたら
    // x + y + z = 0という先決条件を満たせない可能性があり、
    // ここで元の値と一番違う値を破棄し
    // 残った二つの値から改めてその値を計算します。
    if (xDiff > yDiff && xDiff > zDiff) {
        rx = 0 - ry - rz;
    } else if (yDiff > zDiff) {
        ry = 0 - rx - rz;
    } else {
        rz = 0 - rx - ry;
    }

    return new Point(rx, ry, rz);
}  

現在バブル位置のキューブ座標さえ分かれば、あとはその座標をcubeToOffsetで偏移座標に転換し、そのセル周りのセルに何かあるかをチェックすれば、バブルが何かとぶつかっているかも分かるようになります。

繋がっているバブルを探す方法

データストラクチャと衝突検知に続き、最後の課題は繋がっているバブルを探す方法です。
これを必要となる場所は発射されたバブルが他のバブルとぶつかった時同じ色のバブルを探すところ及び天井に繋がっていないバブルを探すところです。
実は、この部分も方法さえ分かれば実装はそんなに難しくありません。
ここで使われる方法はflood fillアルゴリズムです。Flood fillについて具体的な説明はこちらを参照してください。

繋がっている同じ色のバブルを探す

発射されたバブルをスタートポイントとし、検索条件をセルが空きではないことと色が同じであることでflood fillを実行すれば終わりです。

floodFill(shotBubbleCol, shotBubbleRow,
    function(cell) {
        // 検索条件
        return cell.bubble && cell.bubble.getColor() == shotBubbleColor && chainedCells.indexOf(cell) == -1;
    },
    function(cell) {
        // 検索条件に満たすセルに対する処理。ここは該当セルを繋がっているバブルセルのリストに追加することです。
        chainedCells.push(cell);
    });

もちろん、バブルの位置をそのまま使うではなく、まずは行数と列数でポジションを表示する偏移座標へ転換する必要があります。
ここの転換は上に説明した座標転換方法で以下のような転換しましょう：画面座標 → キューブ座標 → 偏移座標。

天井に繋がっていないバブルを探す

ここは先ほどと違って、直接に探すのは困難です。Flood fillは繋がっているものを探すアルゴリズムですから。
なので、考えを逆にして、まず天井に繋がっているバブルを検索して、条件に満たすセルを全部マークすることです。
そうだったら、マークされていない、空きでもないセルはつまり天井に繋がっていないバブルが存在するセルです。

// 第0行（天井に隣接する行）の各セルをスタートポイントとして検索します。
for (var col = 0; col < cellsPerRow; ++col) {
    floodFill(col, 0,
        function(cell) {
            return cell.bubble && !isCellMarked(cell);
        },
        function(cell) {
            markCell(cell);
        });
}

var cellsNotConnectedToCeiling = cells.filter(function(cell) {
    return cell.bubble && !isCellMarked(cell);
});

最後

以上はバブルシューターゲームの基本ゲームプレイを実装する際に解決しなければいけない課題とその解決策です。
勿論、これはゼロから完成までの手順ではありません。あくまで肝心なところだけです。
英語を読める方にこちらのポストがお勧めです。
六角形グリッドに関することをゼロから詳しく説明しています。