2. Pythonで綴る多変量解析 4-2. 因子分析[因子数の推定]

因子数をいくつにするか——。
おおかた見当をつけて因子分析を何ケースか行ない、それらの結果を解釈してみて、もっとも妥当な因子数に決定しています。たとえば、6因子と見当をつけたら、4～6～8因子として5ケース行ない、そのうち分析軸としてもっとも使い勝手のよさそうな因子数を採用するという感じです。
また、因子の解釈に際しては、次のような点に留意しています。
　● 因子の解釈が一意的で、
　● 各因子がなるべく独立的であり、
　● 因子群が全体として網羅的である。

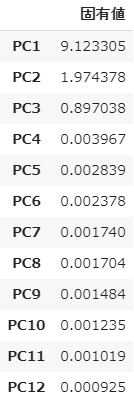
さて、見当をつけるには、主成分分析によって求められる固有値が目安になります。
ひとまず主成分分析のモデル生成までを行ない、その後で因子数を推定する3種類の方法をみていきます。

##1. 主成分分析を行ない固有値を求める
####⑴ ライブラリを読み込む

# 数値計算ライブラリ
import numpy as np
import pandas as pd
# 可視化ライブラリ
import matplotlib.pyplot as plt
%matplotlib inline
# 機械学習ライブラリ
import sklearn

# matplotlibを日本語表記に対応
!pip install japanize-matplotlib
import japanize_matplotlib

####⑵ データを読み込む

# URLを指定してcsvファイルを読み込む
url = 'https://raw.githubusercontent.com/yumi-ito/sample_data/master/subject_scores.csv'
df = pd.read_csv(url)

# 冒頭の5行分を表示
df.head()

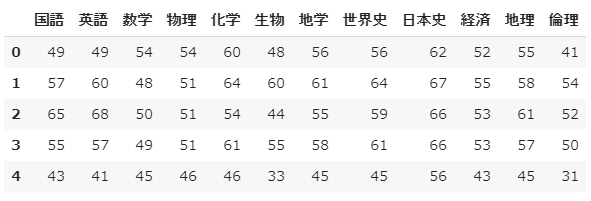
因子分析用に作成したダミーデータ（12教科のテストの得点1000人分）を読み込み、中身を確認します。

####⑶ データを標準化する

# sklearnの標準化メソッドをインポート
from sklearn.preprocessing import StandardScaler

# 標準化の実行
sc = StandardScaler() # インスタンスを生成･定義
sc.fit(df)            # データ変換の計算式を生成
z = sc.transform(df)  # 実際にデータを変換

print("標準化得点：\n", z)
print(" ")
print("行列の形状：", z.shape)

平均を0、分散を1とする標準化得点に変換します。これにより、教科間で得点を単純比較することができます。

####⑷ 主成分分析を行なう

# sklearnのPCA(主成分分析)クラスをインポート
from sklearn.decomposition import PCA

# 主成分分析のモデルを生成
pca = PCA() # インスタンスを生成･定義
pca.fit(z)  # 標準化得点データにもとづいてモデルを生成

以上、主成分分析のモデルが出来たところで、因子数を推定する方法をみていきたいと思います。

##2-1. 因子数の推定－固有値の値をもとにする場合
固有値とは、主成分の分散のことで、主成分の情報量の大きさを表します。まず、固有値が1.0以上の数を因子数とする方法があります。

# 固有値を取得
ev = pca.explained_variance_

# 行名･列名を付与してデータフレームに変換
pd.DataFrame(ev, 
             index=["PC{}".format(x + 1) for x in range(len(df.columns))], 
             columns=["固有値"])

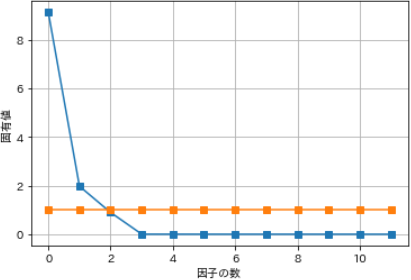
##2-2. 因子数の推定－スクリープロットをもとにする場合
スクリープロットは、固有値を最大値から最小値まで降順でプロットしたグラフのことで、崖のような形を描きます。
スクリー(scree)とは、山の‘がれ場’のこと、岩石がごろごろころがっている急な斜面のことです。固有値が、ある段階から急に小さな値となって以降は安定する段階を因子数とし、それ以下は誤差因子とみなします。

# 基準線(固有値1)をひくためのダミーデータ
ev_1 = np.ones(12)

# 変数を指定
plt.plot(ev, 's-')   # 主成分分析による固有値
plt.plot(ev_1, 's-') # ダミーデータ

# 軸名を指定
plt.xlabel("因子の数")
plt.ylabel("固有値")

plt.grid()
plt.show()

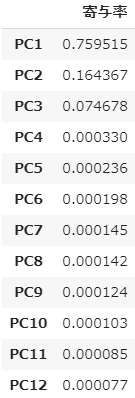
##2-3. 因子数の推定－累積寄与率をもとにする場合

# 寄与率の取得
evr = pca.explained_variance_ratio_

# 行名･列名を付与してデータフレームに変換
pd.DataFrame(evr, 
             index=["PC{}".format(x + 1) for x in range(len(df.columns))], 
             columns=["寄与率"])

寄与率とは、データ全体の情報量（分散）に占める主成分の分散の割合のことです。分散が最大になる主成分を順繰りに抽出してくるので、第1主成分(PC1)がもっとも大きく以降段々に小さくなります。

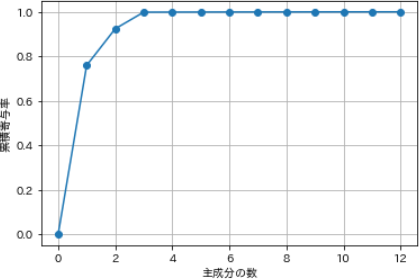
# 起点0と寄与率の累積値をプロット
plt.plot([0] + list(np.cumsum(evr)), "-o")

plt.xlabel("主成分の数")
plt.ylabel("累積寄与率")

plt.grid()
plt.show()

関数numpy.cumsum()は、要素を順次足し合わせたものを配列として返します。
0を起点として、寄与率が累積されていく過程を描画します。主成分を1つ、2つ、3つと加えるにつれて、元のデータ全体の情報量をどの程度カバーできるかがわかります。

##3. 因子数の推定に、なぜ主成分分析なのか？
因子分析と主成分分析とは、目的がまったく異なります。
因子分析は、データに潜在する共通因子を見つけて、データの背後にある構造を知ろうとします。対して、主成分分析は、データのもつ情報を圧縮して次元数を減らし、データを取り扱いやすいように変換してくれます。
ただし、そのやり方はよく似ています。

因子分析は、誤差がなるべく小さくなるような因子負荷量を見つけてきます。因子負荷量とは、共通因子が変数に及ぼしている影響度のことであり、また誤差とは、共通因子以外に各変数が独自にもっている因子のことです。

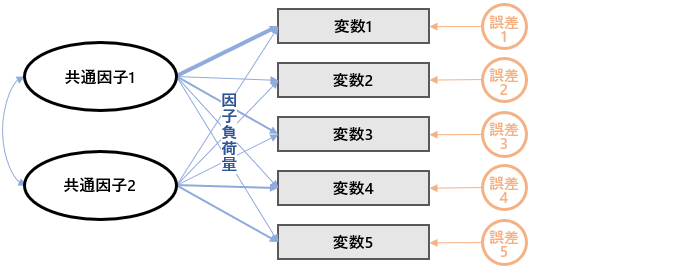
因子分析は、データを共通因子によって説明しようとするものです。
ゆえに、独自因子は誤差として、その分だけ情報を失くすことになります。この情報の損失がなるべく小さくなるような因子負荷量を見つけてくれます。

次いで、主成分分析のパス図を示します。
主成分負荷量は、変数が主成分に及ぼしている影響度です。主成分分析では、情報量＝分散として、情報の保持がなるべく大きくなるような主成分負荷量を見つけます。

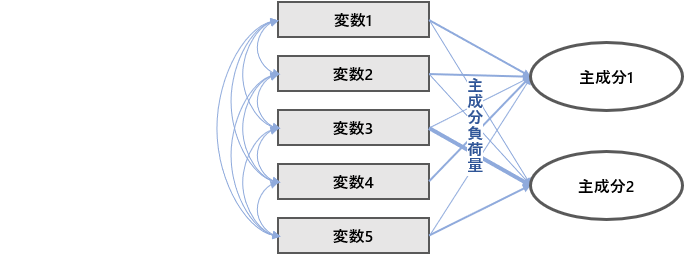
要するに、因子分析と主成分分析は、同じようなことをやっているのです。
目的は違いますし、データの位置づけ（原因側に置くか結果側に置くか）も違いますが、やっていることは共通していて、実際に結果もよく似たものになります。

しかも主成分は、データから自ずと求められるものです。それで、因子数を推定するのに、主成分分析の固有値が目安として利用されます。