1. Pythonで学ぶ統計学 2-3. 正規分布の基本

統計学で一番よく利用される連続型確率分布**「正規分布」**の基本的な事項をまとめます

#1. 正規分布の公式
$$f(x) = \frac{1}{\sqrt{2\pi \sigma}} \exp \left(-\frac{(x - \mu)^2}
{2\sigma^2} \right) \hspace{20px} (-\infty < x < \infty)$$

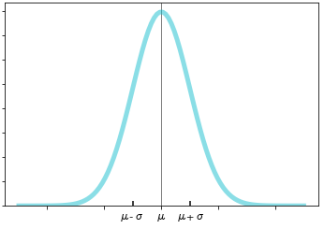
• 正規分布は、上式で定義され、下図のようなベル型の確率密度関数になります
• 正規分布のパラメータは、期待値$μ$、分散$σ^2$、そして分散の平方根は標準偏差です（$標準偏差σ=\sqrt{分散} \hspace{5px}$）
• $π$は円周率、$exp$は「ネイピア数（自然対数の底）」と呼ばれるもので、2.71828（｢鮒一鉢二鉢｣）で近似されます

####⑴ 確率密度関数

• 確率密度関数とは、連続型確率変数の分布を正確に表現したものです
• 連続型確率変数に対して、飛び飛びの値をとる離散型確率変数は、確率分布表やヒストグラムに正確に表現できますが、値$x$が連続する場合、たとえ一定の幅で階級に区切ったとしても階級幅の誤差が生じます
• そうした誤差を解消した確率密度関数は、確率変数$X$の値$x$が、例えば下図のように$a$と$b$の区間にくる確率（=淡黄色部分の面積）を求める関数です

####⑵ 確率密度の計算

• 期待値$μ$、分散$σ^2$をパラメータとする正規分布（normal distribution）は、記号で$N(μ, σ^2) \hspace{5px}$と表現されます
• $N(0, 1^2) \hspace{5px}$の正規分布を仮定し、確率変数$x=0$の確率密度を求めます

import numpy as np

mu = 0
sigma = 1
x = 0

pd = (1 / np.sqrt(2 * np.pi * sigma)) * np.e ** (-(((x - mu)**2) / (2 * sigma**2)))

• scipy.statsを利用して同じく$f(0)$を取得し、突合します

from scipy import stats

mu = 0
sigma = 1
x = 0

X = np.linspace(-5, 5, 100)
norm_pdf = stats.norm.pdf(x=X, loc=mu, scale=sigma) # loc=期待値, scale=標準偏差
stats.norm.pdf(x=0, loc=mu, scale=sigma) # x=確率変数

• いずれも$0.3989422804014327$となります

#2. 正規分布の意義

• 日本の40代男性の平均収入を調べるために、全国の40代男性から無作為に100人を抽出する
• と仮定して、0～800万円の範囲で100人分の乱数を生成したところ、下図のような分布となりました

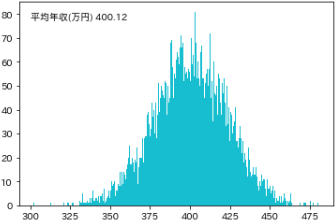
• この「100人抽出して平均値を計算する」ということを10,000回くり返します
• つまり10,000個の平均収入が得られることになりますが、それをヒストグラムに表したのが下図です
• つまり、標本毎に平均値はまちまちですが、その確率密度関数は正規分布になります

#3. 正規分布の性質

• 正規分布のグラフは、期待値を中心として左右対称のベル型をしています

####⑴ 現象が起こる確率

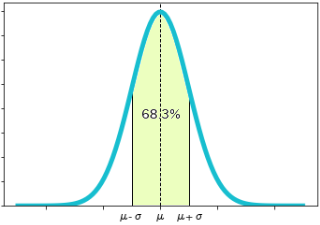
• ある区間の現象が起こる確率は、その区間で確率密度関数の曲線と横軸に囲まれた部分の面積で表されます
• 「期待値±標準偏差」の区間に68%以上の面積が入ります

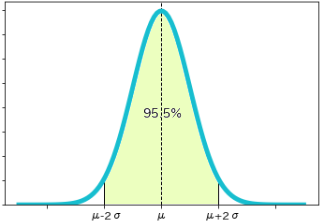
• 「期待値±2×標準偏差」の区間に95%以上の面積が入ります

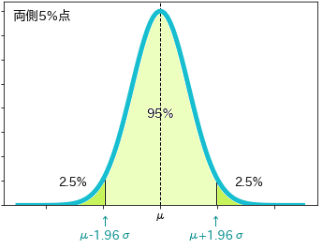
####⑵ パーセント点

• 平均値を中心に95%を占める範囲を示す境界点、$μ-1.96σ$と$μ+1.96σ$を両側5%点

• 同じく99%を占める範囲を示す境界点、$μ-2.58σ$と$μ+2.58σ$を両側1%点と呼びます

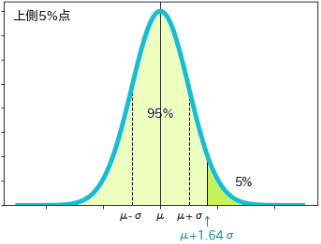
####⑶ 上側パーセント点

• また上側のみ、すなわちx軸の左側から右側へ95%の範囲にあたる境界点、$μ+1.64σ$は上側5%点

• 同じくx軸の左側から右側へ99%の範囲にあたる境界点、$μ+2.33σ$が上側1%点になります

#4. 標準正規分布

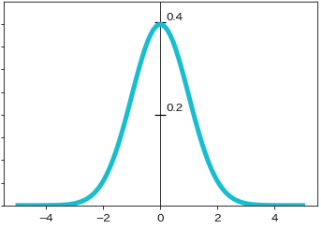
• 期待値$μ$を$0$、標準偏差$σ$を$1$（分散$1^2$）とする正規分布を標準正規分布といい、次式に定義されます

$$標準正規分布f(x) = \frac{1}{\sqrt{2\pi}} \exp \left(-\frac{x^2}
{2} \right) \hspace{20px}$$

• 先に計算した$N(0, 1^2) \hspace{5px}$の確率密度関数$f(0)=0.3989422804014327$と一致しています

Appendix

# 数値計算ライブラリ
import numpy as np
from scipy import stats

# グラフ描画ライブラリ
import matplotlib.pyplot as plt
%matplotlib inline

# matplotlibの日本語表示対応モジュール
!pip install japanize-matplotlib
import japanize_matplotlib

1．正規分布の公式

# 期待値・標準偏差を指定
mu = 0
sigma = 1

# 等差数列を生成
X = np.linspace(-5, 5, 100)

# pdfで確率密度関数を生成
norm_pdf = stats.norm.pdf(x=X, loc=mu, scale=sigma) # 期待値=0, 標準偏差=1
norm_pdf_max = np.max(norm_pdf) # 確率密度の最大値

# グラフ描画
plt.plot(X, norm_pdf, lw=5, color="tab:cyan", alpha=0.5)

# 垂直線
plt.vlines(0, 0, norm_pdf_max + 0.02, color="black", lw=0.5) # 期待値
plt.vlines(mu-sigma, 0, 0.01, color="black", lw=1.5) # %点(μ-σ)
plt.vlines(mu+sigma, 0, 0.01, color="black", lw=1.5) # %点(μ+σ)

# 軸目盛
plt.xticks(color="None") # x軸目盛を消去
plt.yticks(color="None") # y軸目盛を消去
plt.ylim(0, norm_pdf_max + 0.02) # y軸目盛範囲

# テキスト
plt.text(-0.2, -0.03, 'μ', fontsize = 12) # μ
plt.text(-1.5, -0.03, 'μ-σ', fontsize = 12) # μ-σ
plt.text(0.5, -0.03, 'μ+σ', fontsize = 12) # μ+σ

plt.show()

⑴ 確率密度関数

# 期待値・標準偏差を指定
mu = 30
sigma = 20
# 任意のx値
xa = 10
xb = 20

# 等差数列を生成
X = np.arange(0, 100, 0.1)

# pdfで確率密度関数を生成
norm_pdf = stats.norm.pdf(x=X, loc=mu, scale=sigma) # 期待値=30, 標準偏差=20
# 確率密度を取得
norm_pdf_max = np.max(norm_pdf) # 確率密度の最大値
ya = stats.norm.pdf(x=xa, loc=30, scale=20) # 確率変数xa
yb = stats.norm.pdf(x=xb, loc=30, scale=20) # 確率変数xb

# グラフ描画
plt.plot(X, norm_pdf, lw=5, color="tab:cyan", alpha=0.5)

plt.vlines(10, 0, ya, color="black", lw=1.2) # a点の垂直線
plt.vlines(20, 0, yb, color="black", lw=1.2) # b点の垂直線

plt.xticks(color="None") # x軸目盛ラベルを消去
plt.yticks(color="None") # y軸目盛ラベルを消去
plt.ylim(0, norm_pdf_max + 0.001) # y軸目盛範囲を指定

plt.text(10-0.9, -0.0015, 'a', fontsize = 12) # text(a)を配置
plt.text(20-0.9, -0.0015, 'b', fontsize = 12) # text(b)を配置

plt.show()

2．正規分布の意義

import random

# 乱数を生成
random.seed(0) # 乱数シードを固定
X = [random.randint(0, 800) for i in range(100)]

# 平均値を取得
mu = sum(X)/len(X)

# ヒストグラム描画
plt.hist(X, color = 'tab:cyan', rwidth = 0.9)
plt.text( 0.02, 15.5, f'平均年収(万円) {mu:.2f}')

plt.show()

# 標本平均を格納する変数
averages = []

# 100人抽出を10,000回試行
for i in range(10000):
    random.seed(i)
    X = [random.randint(0, 800) for i in range(100)]
    average = sum(X)/len(X)
    averages.append(average)

# 平均値を取得
mu = sum(averages)/len(averages)

# ヒストグラムを描画
plt.hist(averages, color = 'tab:cyan', bins=500)
plt.text(300, 78, f'平均年収(万円) {mu:.2f}')

plt.show()

3．正規分布の性質
⑴ 現象が起こる確率

# 期待値・標準偏差を指定
mu = 0
sigma = 1

# 等差数列を生成
X = np.linspace(-5, 5, 100)

# pdfで確率密度関数を生成
norm_pdf = stats.norm.pdf(x=X, loc=mu, scale=sigma) # 期待値=0, 標準偏差=1
# 確率密度を取得
norm_pdf_max = np.max(norm_pdf) # 確率密度の最大値
lower = stats.norm.pdf(x=mu-sigma, loc=mu, scale=sigma) #確率変数μ-σ
upper = stats.norm.pdf(x=mu+sigma, loc=mu, scale=sigma) #確率変数μ+σ

# グラフ描画
plt.plot(X, norm_pdf, lw=5, color="tab:cyan")

# 垂直線
plt.vlines(0, 0, norm_pdf_max + 0.02, color="black", lw=1, linestyle='--') # 期待値
plt.vlines(mu-sigma, 0, lower, color="black", lw=1) # %点(μ-σ)
plt.vlines(mu+sigma, 0, upper, color="black", lw=1) # %点(μ+σ)

# 軸目盛
plt.xticks(color="None") # x軸目盛を消去
plt.yticks(color="None") # y軸目盛を消去
plt.ylim(0, norm_pdf_max + 0.02) # y軸目盛範囲を指定

# テキストを配置
plt.text(-0.2, -0.03, 'μ', fontsize = 12) # μ
plt.text(-1.5, -0.03, 'μ-σ', fontsize = 12) # μ-σ
plt.text(0.5, -0.03, 'μ+σ', fontsize = 12) # μ+σ
plt.text(-0.65, 0.18, '68.3%', fontsize = 14) # 68.3%

plt.show()

# 期待値・標準偏差を指定
mu = 0
sigma = 1

# 等差数列を生成
X = np.linspace(-5, 5, 100)

# pdfで確率密度関数を生成
norm_pdf = stats.norm.pdf(x=X, loc=mu, scale=sigma) # 期待値=0, 標準偏差=1

# 確率密度を取得
norm_pdf_max = np.max(norm_pdf) # 確率密度の最大値
lower = stats.norm.pdf(x=mu-2*sigma, loc=mu, scale=sigma) #確率変数μ-2σ
upper = stats.norm.pdf(x=mu+2*sigma, loc=mu, scale=sigma) #確率変数μ+2σ

# グラフ描画
plt.plot(X, norm_pdf, lw=5, color="tab:cyan")

# 垂直線
plt.vlines(0, 0, norm_pdf_max + 0.02, color="black", lw=1, linestyle='--') # 期待値
plt.vlines(mu-2*sigma, 0, lower, color="black", lw=1) # %点(μ-2σ)
plt.vlines(mu+2*sigma, 0, upper, color="black", lw=1) # %点(μ+2σ)

# 軸目盛
plt.xticks(color="None") # x軸目盛を消去
plt.yticks(color="None") # y軸目盛を消去
plt.ylim(0, norm_pdf_max + 0.02) # y軸目盛範囲を指定

# テキストを配置
plt.text(-0.2, -0.03, 'μ', fontsize = 12) # μ
plt.text(-2.5, -0.03, 'μ-2σ', fontsize = 12) # μ-2σ
plt.text(1.5, -0.03, 'μ+2σ', fontsize = 12) # μ+2σ
plt.text(-0.65, 0.18, '95.5%', fontsize = 14) # 95.5%

plt.show()

⑵ パーセント点

# 期待値・標準偏差を指定
mu = 0
sigma = 1

# 等差数列を生成
X = np.linspace(-5, 5, 100)

# pdfで確率密度関数を生成
norm_pdf = stats.norm.pdf(x=X, loc=mu, scale=sigma) # 期待値=0, 標準偏差=1

# 確率密度を取得
norm_pdf_max = np.max(norm_pdf) # 確率密度の最大値
lower = stats.norm.pdf(x=mu-1.96*sigma, loc=mu, scale=sigma) #確率変数μ-1.96
upper = stats.norm.pdf(x=mu+1.96*sigma, loc=mu, scale=sigma) #確率変数μ+1.96

# グラフ描画
plt.plot(X, norm_pdf, lw=5, color="tab:cyan")

# 垂直線
plt.vlines(0, 0, norm_pdf_max + 0.02, color="black", lw=1, linestyle='--') # 期待値
plt.vlines(mu-1.96*sigma, 0, lower, color="black", lw=1) # %点(μ-1.96σ)
plt.vlines(mu+1.96*sigma, 0, upper, color="black", lw=1) # %点(μ+1.96σ)

# 軸目盛
plt.xticks(color="None") # x軸目盛を消去
plt.yticks(color="None") # y軸目盛を消去
plt.ylim(0, norm_pdf_max + 0.02) # y軸目盛範囲を指定

# テキストを配置
plt.text(-0.2, -0.03, 'μ', fontsize = 12) # μ
plt.text(-1.95, -0.07, '↑\nμ-1.96σ', fontsize = 13, horizontalalignment='center', color="darkcyan") # μ-1.96σ
plt.text(1.95, -0.07, '↑\nμ+1.96σ', fontsize = 13, horizontalalignment='center', color="darkcyan") # μ+1.96σ
plt.text(-0.5, 0.18, '95%', fontsize = 14) # 95%
plt.text(2.6, 0.04, '2.5%', fontsize = 13) # 2.5%
plt.text(-3.6, 0.04, '2.5%', fontsize = 13) # 2.5%
plt.text(-5.2, 0.38, '両側5%点', fontsize = 14) # 両側5%点

plt.show()

# 期待値・標準偏差を指定
mu = 0
sigma = 1

# 等差数列を生成
X = np.linspace(-5, 5, 100)

# pdfで確率密度関数を生成
norm_pdf = stats.norm.pdf(x=X, loc=mu, scale=sigma) # 期待値=0, 標準偏差=1

# 確率密度を取得
norm_pdf_max = np.max(norm_pdf) # 確率密度の最大値
lower = stats.norm.pdf(x=mu-2.58*sigma, loc=mu, scale=sigma) #確率変数μ-2.58σ
upper = stats.norm.pdf(x=mu+2.58*sigma, loc=mu, scale=sigma) #確率変数μ+2.58σ

# グラフ描画
plt.plot(X, norm_pdf, lw=5, color="tab:cyan")

# 垂直線
plt.vlines(0, 0, norm_pdf_max + 0.02, color="black", lw=1, linestyle='--') # 期待値
plt.vlines(mu-2.58*sigma, 0, lower, color="black", lw=1) # %点(μ-2.58σ)
plt.vlines(mu+2.58*sigma, 0, upper, color="black", lw=1) # %点(μ+2.58σ)

# 軸目盛
plt.xticks(color="None") # x軸目盛を消去
plt.yticks(color="None") # y軸目盛を消去
plt.ylim(0, norm_pdf_max + 0.02) # y軸目盛範囲を指定

# テキストを配置
plt.text(-0.2, -0.03, 'μ', fontsize = 12) # μ
plt.text(-2.55, -0.07, '↑\nμ-2.58σ', fontsize = 13, horizontalalignment='center', color="darkcyan") # μ-2.58σ
plt.text(2.6, -0.07, '↑\nμ+2.58σ', fontsize = 13, horizontalalignment='center', color="darkcyan") # μ+2.58σ
plt.text(-0.5, 0.18, '99%', fontsize = 14) # 99%
plt.text(2.6, 0.04, '0.5%', fontsize = 13) # 0.5%
plt.text(-3.6, 0.04, '0.5%', fontsize = 13) # 0.5%
plt.text(-5.2, 0.38, '両側1%点', fontsize = 14) # 両側1%点

plt.show()

⑶ 上側パーセント点

# 期待値・標準偏差を指定
mu = 0
sigma = 1

# 等差数列を生成
X = np.linspace(-5, 5, 100)

# pdfで確率密度関数を生成
norm_pdf = stats.norm.pdf(x=X, loc=mu, scale=sigma) # 期待値=0, 標準偏差=1

# 確率密度を取得
norm_pdf_max = np.max(norm_pdf) # 確率密度の最大値
upper_1 = stats.norm.pdf(x=mu+1.64*sigma, loc=mu, scale=sigma) # 確率変数μ+1.64σ
lower = stats.norm.pdf(x=mu-sigma, loc=mu, scale=sigma) # 確率変数μ-σ
upper_2 = stats.norm.pdf(x=mu+sigma, loc=mu, scale=sigma) # 確率変数μ+σ

# グラフ描画
plt.plot(X, norm_pdf, lw=5, color="tab:cyan")

# 垂直線
plt.vlines(0, 0, norm_pdf_max + 0.02, color="black", lw=0.8) # μ
plt.vlines(mu+1.64*sigma, 0, upper_1, color="black", lw=1.2) # 上側5%点(μ+1.64σ)
plt.vlines(mu-sigma, 0, lower, color="black", lw=1, linestyle='--') # %点(μ-σ)
plt.vlines(mu+sigma, 0, upper_2, color="black", lw=1, linestyle='--') # %点(μ+σ)

# 軸目盛
plt.xticks(color="None") # x軸ラベルを消去
plt.yticks(color="None") # y軸ラベルを消去
plt.ylim(0, norm_pdf_max + 0.02) # y軸目盛範囲を指定

# テキストを配置
plt.text(-0.2, -0.03, 'μ', fontsize = 12) # μ
plt.text(1.65, -0.07, '↑\nμ+1.64σ', fontsize = 13, horizontalalignment='center', color="darkcyan") # μ+1.64σ
plt.text(-0.5, 0.18, '95%', fontsize = 14) # 95%
plt.text(2.6, 0.04, '5%', fontsize = 13) # 5%
plt.text(-5.2, 0.38, '上側5%点', fontsize = 14) # 上側5%点
plt.text(-1.5, -0.03, 'μ-σ', fontsize = 12) # μ-σ
plt.text(0.5, -0.03, 'μ+σ', fontsize = 12) # μ+σ

plt.show()

# 期待値・標準偏差を指定
mu = 0
sigma = 1

# 等差数列を生成
X = np.linspace(-5, 5, 100)

# pdfで確率密度関数を生成
norm_pdf = stats.norm.pdf(x=X, loc=mu, scale=sigma) # 期待値=0, 標準偏差=1

# 確率密度を取得
norm_pdf_max = np.max(norm_pdf) # 確率密度の最大値
upper_1 = stats.norm.pdf(x=mu+2.33*sigma, loc=mu, scale=sigma) # 確率変数μ+2.33σ
lower = stats.norm.pdf(x=mu-sigma, loc=mu, scale=sigma) # 確率変数μ-σ
upper_2 = stats.norm.pdf(x=mu+sigma, loc=mu, scale=sigma) # 確率変数μ+σ

# グラフ描画
plt.plot(X, norm_pdf, lw=5, color="tab:cyan")

# 垂直線
plt.vlines(0, 0, norm_pdf_max + 0.02, color="black", lw=0.8) # μ
plt.vlines(mu+2.33*sigma, 0, upper_1, color="black", lw=1.2) # 上側1%点(μ+2.33σ)
plt.vlines(mu-sigma, 0, lower, color="black", lw=1, linestyle='--') # %点(μ-σ)
plt.vlines(mu+sigma, 0, upper_2, color="black", lw=1, linestyle='--') # %点(μ+σ)

# 軸目盛
plt.xticks(color="None") # x軸ラベルを消去
plt.yticks(color="None") # y軸ラベルを消去
plt.ylim(0, norm_pdf_max + 0.02) # y軸目盛範囲を指定

# テキストを配置
plt.text(-0.2, -0.03, 'μ', fontsize = 12) # μ
plt.text(2.35, -0.07, '↑\nμ+2.33σ', fontsize = 13, horizontalalignment='center', color="darkcyan") # μ+2.33σ
plt.text(-0.5, 0.18, '99%', fontsize = 14) # 99%
plt.text(2.6, 0.04, '1%', fontsize = 13) # 1%
plt.text(-5.2, 0.38, '上側1%点', fontsize = 14) # 上側1%点
plt.text(-1.5, -0.03, 'μ-σ', fontsize = 12) # μ-σ
plt.text(0.5, -0.03, 'μ+σ', fontsize = 12) # μ+σ

plt.show()

4．標準正規分布

# 期待値・標準偏差を指定
mu = 0
sigma = 1

# 等差数列を生成
X = np.linspace(-5, 5, 100)

# pdfで確率密度関数を生成
norm_pdf = stats.norm.pdf(x=X, loc=mu, scale=sigma) # 期待値=0, 標準偏差=1

# 確率密度を取得
norm_pdf_max = np.max(norm_pdf) # 確率密度の最大値

# グラフ描画
plt.plot(X, norm_pdf, lw=5, color="tab:cyan")

# 垂直線を描画
plt.vlines(0, 0, norm_pdf_max + 0.05, color="black", lw=0.8) # 期待値
plt.hlines(0.2, -0.2, 0.2, color="black", lw=1.2) # 水平線
plt.hlines(0.403, -0.2, 0.2, color="black", lw=1.2) # 水平線

# 軸目盛を調整
plt.yticks(color="None") # y軸ラベルを消去
plt.xticks(fontsize=12) # x軸ラベルのフォントサイズ
plt.ylim(0, norm_pdf_max + 0.05) # y軸目盛範囲

# テキストを配置
plt.text(0.2, 0.21, '0.2', fontsize = 12) # 0.2
plt.text(0.2, 0.41, '0.4', fontsize = 12) # 0.4

plt.show()