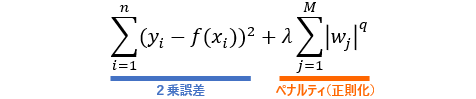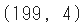2. Pythonで綴る多変量解析 6-1. リッジ回帰･ラッソ回帰(scikit-learn)[重回帰vsリッジ回帰]

• 平たく言えば、どちらも重回帰分析の進化形で、ラッソ(Lasso)はL1、リッジ(Ridge)はL2とも呼ばれ、双子のような関係です。
• どういう進化かといえば、重回帰分析を過学習が起こりにくいように改良したというものです。
• 重回帰分析では、損失関数（予測値と目的変数の２乗和誤差）が最小になるように回帰係数を推定しますが、これに加えて、回帰係数そのものが大きくなることを避ける工夫が施されています。
• 一般的に、回帰係数が大きいモデルは、入力の小さな動きで出力が大きく動きます。そのような過敏なモデルは、訓練データには当てはまっても未知のデータにはうまく当てはまらないリスクが高いといえます。
• そこで、損失関数に変数の数や重みが増えるほどペナルティが加算されるようにして、モデル自身にパラメータの大きさを抑制してもらいます。

• 上の式は、ペナルティを加えた損失関数の定義で、ペナルティのことを正確には正則化(regularization)といいます。
• 変数の数$M$が増えるほど、重み$W$も増えるほど、正則化項の値が大きくなり、それが加算されて損失関数の値が大きくなるというしくみです。
• なお、正則化項の$q$が、$q=1$のときをラッソ回帰、$q=2$のときをリッジ回帰と呼びます。

⑴ ライブラリのインポート

# データ加工・計算・分析ライブラリ
import numpy as np
import pandas as pd

# グラフ描画ライブラリ
import matplotlib.pyplot as plt
%matplotlib inline

# 機械学習ライブラリ
import sklearn

⑵ データの取得と読み込み

# データを取得
url = 'https://raw.githubusercontent.com/yumi-ito/datasets/master/datasets_auto.csv'

# 取得したデータをDataFrameオブジェクトとして読み込み
df = pd.read_csv(url, header=None)

# 列ラベルを設定
df.columns = ['symboling', 'normalized-losses', 'make', 'fuel-type', 'aspiration', 'num-of-doors', 'body-style', 'drive-wheels', 'engine-location', 'wheel-base', 
              'length', 'width', 'height', 'curb-weight', 'engine-type', 'num-of-cylinders', 'engine-size', 'fuel-system', 'bore', 'stroke', 
              'compression-ratio', 'horsepower', 'peak-rpm', 'city-mpg', 'highway-mpg', 'price']

• 自動車のボディスタイル、車体の大きさ、燃費など諸々の仕様、及び保険リスク格付けなどの属性情報をもとに、自動車価格を予測するデータセットです。
• アメリカにおける1985年モデルの輸入車・トラックのデータで、ウォード自動車年鑑1985年版、保険サービス事務所の個人用自動車マニュアル、道路安全保険協会の保険衝突報告書という３つのソースから抽出されたものです。詳細はこちら。https://archive.ics.uci.edu/ml/datasets/Automobile
• 概要を以下に整理しました。説明変数は、数値型・属性型を合わせて全25個あります。目的変数は価格で、標本数は205件となっています。

	変数名	意訳	項目（解説）	データ型
0	symboling	保険リスク格付け	-3, -2, -1, 0, 1, 2, 3.（3は高リスクで危険、-3は低リスクで安全）	int64
1	normalized-losses	正規化損失	65〜256	object
2	make	メーカー	alfa-romero, audi, bmw, ..., volkswagen, volvo.	object
3	fuel-type	燃料タイプ	diesel, gas.	object
4	aspiration	吸気タイプ	std, turbo.	object
5	num-of-doors	ドア数	four, two.	object
6	body-style	ボディスタイル	hardtop, wagon, sedan, hatchback, convertible.	object
7	drive-wheels	駆動輪	4wd, fwd, rwd.	object
8	engine-location	エンジン位置	front, rear.	object
9	wheel-base	ホイールベース	86.6～120.9	float64
10	length	車長	141.1～208.1	float64
11	width	車幅	60.3～72.3	float64
12	height	車高	47.8～59.8	float64
13	curb-weight	無人車重	1488～4066	int64
14	engine-type	エンジンタイプ	dohc, dohcv, l, ohc, ohcf, ohcv, rotor.	object
15	num-of-cylinders	気筒数	eight, five, four, six, three, twelve, two.	object
16	engine-size	エンジンサイズ	61～326	int64
17	fuel-system	燃料システム	1bbl, 2bbl, 4bbl, idi, mfi, mpfi, spdi, spfi.	object
18	bore	エンジンのシリンダー内径	2.54～3.94	object
19	stroke	ピストンの移動量	2.07～4.17	object
20	compression-ratio	圧縮比	7～23	float64
21	horsepower	馬力	48～288	object
22	peak-rpm	最高出力	4150～6600	object
23	city-mpg	街中燃費	13～49（石油1ガロンあたりの走行マイル数）	int64
24	highway-mpg	高速道路 燃費	16～54	int64
25	price	価格	5118～45400	object

# データの形状と欠損数を出力
print(df.shape)
print('欠損の数：{}'.format(df.isnull().sum().sum()))

# データの先頭5行を出力
df.head()

⑶ データの前処理

• まず、ここではhorsepower(馬力)、width(車幅)、height(車高)という３つの説明変数だけを対象とすることにします。
• なお、このデータセットには｢?｣という処理のできない値が含まれているので、これを含む標本を削除しなければなりません。

# 対象となる列だけのDataFrameを作成
auto = df[['price', 'horsepower', 'width', 'height']]

# 列ごとに｢?｣が含まれている数を確認
auto.isin(['?']).sum()

# ｢?｣をNANに置換し、NANがある行を削除
auto = auto.replace('?', np.nan).dropna()

# 削除後の行列の形状を確認
auto.shape

• 行数がもとの205から｢?｣を含む6行分をひいた199になっていること、また、対象とする4変数だけの行列となっていることを確認しました。
• さらに、この4変数のデータ型を確認します。

# データ型の確認
auto.dtypes

• object型はstr型に等しく、数値型に変換する必要があります。

# データ型を変換
auto = auto.assign(price = pd.to_numeric(auto.price))
auto = auto.assign(horsepower = pd.to_numeric(auto.horsepower))

# 変換後のデータ型を確認
auto.dtypes

• pandasのassign()関数は、キーワード引数に列名 = 値を指定すると、既存の列には指定した値が代入され、新規の列名の場合は新たに列が追加されます。
• では、データ前処理の最後にpandasのcorr()関数で相関行列を確認しておきます。

auto.corr()

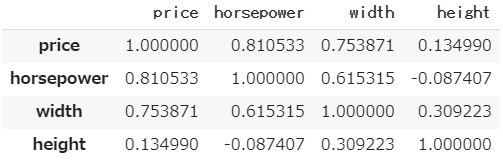
• priceは目的変数なので、それ以外の説明変数間での相関係数を観察すると、widthとhorsepowerの相関係数が0.6以上とやや高くなっています。
• 重回帰分析において、説明変数間で高い相関がみられる場合、相関の高い変数群を代表する変数のみを使います。多重共線性（通称マルチコ）と呼ばれる現象で、説明変数間の高い相関によって計算に不具合を生じたり、係数やオッズ比が異常な値をとったりするからです。
• とはいえ、これはテストなので、このまま説明変数を３つとも使うこととします。

⑷ モデルの構築と評価

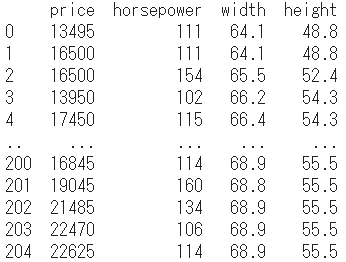
# データを確認
print(auto)

このデータをつかって、リッジ回帰と重回帰分析それぞれのモデル推定を行ない、両者の精度を比較してみます。

# リッジ回帰のモデル構築のためのインポート
from sklearn.linear_model import Ridge

# 重回帰分析のモデル構築のためのインポート
from sklearn.linear_model import LinearRegression

# データ分割（訓練データとテストデータ）のためのインポート
from sklearn.model_selection import train_test_split

• pandasのdrop()関数でprice列を削除して説明変数のみをxとし、またpriceのみをyと設定します。
• sklearnのtrain_test_splitメソッドで、説明変数x、目的変数yをそれぞれ訓練データ(train)とテストデータ(test)に分けます。

# 説明変数と目的変数を設定
x = auto.drop('price', axis=1)
y = auto['price']

# 訓練データとテストデータに分割
X_train, X_test, Y_train, Y_test = train_test_split(x, y, test_size=0.5, random_state=0)

まず、重回帰分析のモデルを構築し、訓練データとテストデータの正解率を算出します。

# LinearRegressionクラスの初期化
linear = LinearRegression()

# 学習の実行
linear.fit(X_train, Y_train)

# 訓練データの正解率
train_score_linear = format(linear.score(X_train, Y_train))
print('重回帰分析の正解率(train):', 
      '{:.6f}'.format(float(train_score_linear)))

# テストデータの正解率
test_score_linear = format(linear.score(X_test, Y_test))
print('重回帰分析の正解率(test):', 
      '{:.6f}'.format(float(test_score_linear)))

• '{:.桁数f}'.format()で小数点以下の桁数を指定しています。
• train_score_linearとtest_score_linearはデータ型がstr型なので、float()で浮動小数点数に変換しています。

次に、リッジ回帰のモデルを構築し、訓練データとテストデータの正解率を算出します。

# Ridgeクラスの初期化
ridge = Ridge()

# 学習の実行
ridge.fit(X_train, Y_train)

# 訓練データの正解率
train_score_ridge = format(ridge.score(X_train, Y_train))
print('リッジ回帰の正解率(train):', 
      '{:.6f}'.format(float(train_score_ridge)))

# テストデータの正解率
test_score_ridge = format(ridge.score(X_test, Y_test))
print('リッジ回帰の正解率(test):', 
      '{:.6f}'.format(float(test_score_ridge)))

	重回帰分析(L)	リッジ回帰(R)	差分(L-R)
訓練データの正解率	0.733358	0.733355	0.000003
テストデータの正解率	0.737069	0.737768	-0.000699

• これらのモデルにおいては、重回帰とリッジ回帰の性能に大きな差はみられません。
• ただ傾向として、訓練データの学習では重回帰の方が微小ながら正解率は高く、それがテストデータになるとリッジ回帰の方が逆転しています。この逆転が、正則化による効果とみて良さそうです。