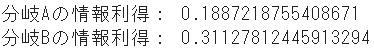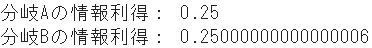2. Pythonで綴る多変量解析 7-2. 決定木[分割基準の違い]

• 決定木における分類の分割基準はいくつかあります。
• 一般的に使用されているものに、ジニ不純度（gini impurity）、エントロピー（entropy）という２つの不純物測定と、それから分類誤差（misclassification error）という分割基準があります。
• これらの違いを見ていきます。

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

２クラス分類での各指標の比較

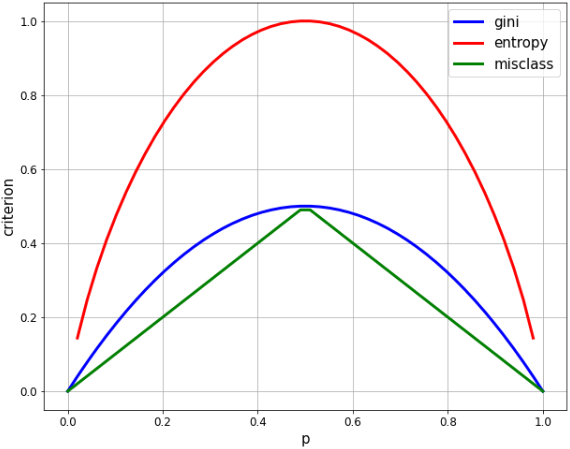
• ２クラス分類で、一方のクラスの割合を p とすると、各指標はそれぞれ次のように求められます。
• ジニ(gini): $2p * (1-p)$
• エントロピー(entropy): $-p * \log p-(1-p) * log(1-p)$
• 誤分類率(misclassification rate): $1-max(p, 1-p)$

# p に相当する等差数列を生成
xx = np.linspace(0, 1, 50) # 開始値0、終了値1、要素数50

plt.figure(figsize=(10, 8))

# 各指標を計算
gini = [2 * x * (1-x) for x in xx]
entropy = [-x * np.log2(x) - (1-x) * np.log2(1-x)  for x in xx]
misclass = [1 - max(x, 1-x) for x in xx]

# グラフを表示
plt.plot(xx, gini, label='gini', lw=3, color='b')
plt.plot(xx, entropy, label='entropy', lw=3, color='r')
plt.plot(xx, misclass, label='misclass', lw=3, color='g')

plt.xlabel('p', fontsize=15)
plt.ylabel('criterion', fontsize=15)
plt.legend(fontsize=15)
plt.xticks(fontsize=12) 
plt.yticks(fontsize=12) 
plt.grid()

• ２クラスの割合が均等のとき(p=0.5)、いずれも最大値となりますが、
• エントロピーの最大値は 1.0、ジニは 0.5 なので、比較しやすいようにエントロピーの方を1/2の係数でスケーリングします。

# p に相当する等差数列を生成
xx = np.linspace(0, 1, 50) # 開始値0、終了値1、要素数50

plt.figure(figsize=(10, 8))

# 各指標を計算
gini = [2 * x * (1-x) for x in xx]
entropy = [(x * np.log((1-x)/x) - np.log(1-x)) / (np.log(2))  for x in xx]
entropy_scaled = [(x * np.log((1-x)/x) - np.log(1-x)) / (2*np.log(2))  for x in xx]
misclass = [1 - max(x, 1-x) for x in xx]

# グラフを表示
plt.plot(xx, gini, label='gini', lw=3, color='b')
plt.plot(xx, entropy, label='entropy', lw=3, color='r', linestyle='dashed')
plt.plot(xx, entropy_scaled, label='entropy(scaled)', lw=3, color='r')
plt.plot(xx, misclass, label='misclass', lw=3, color='g')

plt.xlabel('p', fontsize=15)
plt.ylabel('criterion', fontsize=15)
plt.legend(fontsize=15)
plt.xticks(fontsize=12) 
plt.yticks(fontsize=12) 
plt.grid()

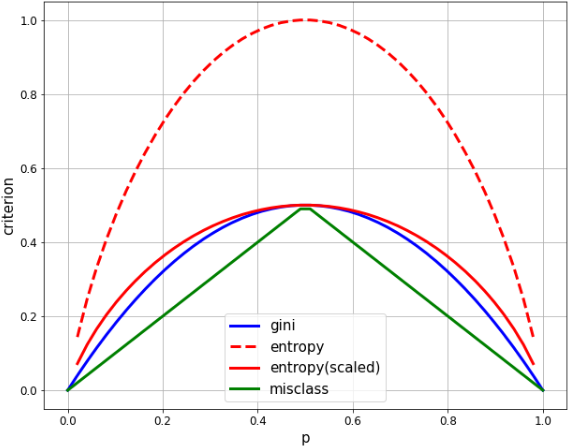
• ジニ(gini)とエントロピー(entropy)はよく似ていて、どちらも二次曲線を描いて p = 1/2 で最大化しています。
• 誤分類率(misclass)は、線形であるという点で明らかに異なりますが、多くの同じ特性を共有しています。p = 1/2 で最大化し、p = 0, 1 でゼロに等しく、山なりに変化しています。

情報利得にみる各指標の違い

1. 情報利得とは

• 情報利得(information gain)とは、ある変数を使ってデータを分割したとき、分割の前後でどれだけ不純度が減少したかを表す指標です。
• 不純度が減れば減るほど、その変数は分類条件として有益だということになります。
• その意味で、いかに不純度を低減できるか、ということは各分岐における情報利得の最大化と同義といえます。
• ２クラス分類の場合、情報利得(IG)は次の式に定義されます。
• $\displaystyle IG(D_{p}, a) = I(D_{p}) - \frac{N_{left}}{N} I(D_{left}) - \frac{N_{right}}{N} I(D_{right})$
• $I$は不純度を意味し、$D_{p}$は親(parent)ノードのデータ、子ノードのデータの左右が$D_{left}$と$D_{right}$で、また親ノードのサンプル数$N$を分母として子ノードの左右それぞれの割合となっています。

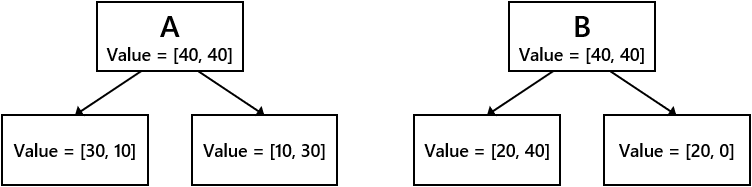
2. 各指標での情報利得を計算する

• 次のような２通りの分岐条件A, Bを仮定します。
• ジニ、エントロピー、誤分類率のそれぞれについて、分岐条件A, B間での情報利得を比較します。

➀ジニ不純度による情報利得

# 親ノードのジニ不純度
IGg_p = 2 * 1/2 * (1-(1/2))

# 子ノードAのジニ不純度
IGg_A_l = 2 * 3/4 * (1-(3/4)) # 左
IGg_A_r = 2 * 1/4 * (1-(1/4)) # 右
# 子ノードBのジニ不純度
IGg_B_l = 2 * 2/6 * (1-(2/6)) # 左
IGg_B_r = 2 * 2/2 * (1-(2/2)) # 右

# 各分岐の情報利得
IG_gini_A = IGg_p - 4/8 * IGg_A_l - 4/8 * IGg_A_r
IG_gini_B = IGg_p - 6/8 * IGg_B_l - 2/8 * IGg_B_r

print("分岐Aの情報利得：", IG_gini_A)
print("分岐Bの情報利得：", IG_gini_B)

➁エントロピーによる情報利得

# 親ノードのエントロピー
IGe_p = (4/8 * np.log((1-4/8)/(4/8)) - np.log(1-4/8)) / (np.log(2))

# 子ノードAのエントロピー
IGe_A_l = (3/4 * np.log((1-3/4)/(3/4)) - np.log(1-3/4)) / (np.log(2)) # 左
IGe_A_r = (1/4 * np.log((1-1/4)/(1/4)) - np.log(1-1/4)) / (np.log(2)) # 右
# 子ノードBのエントロピー
IGe_B_l = (2/6 * np.log((1-2/6)/(2/6)) - np.log(1-2/6)) / (np.log(2)) # 左
IGe_B_r = (2/2 * np.log((1-2/2+1e-7)/(2/2)) - np.log(1-2/2+1e-7)) / (np.log(2)) # 右、+1e-7は0除算回避のために微小値を加算

# 各分岐の情報利得
IG_entropy_A = IGe_p - 4/8 * IGe_A_l - 4/8 * IGe_A_r
IG_entropy_B = IGe_p - 6/8 * IGe_B_l - 2/8 * IGe_B_r
print("分岐Aの情報利得：", IG_entropy_A)
print("分岐Bの情報利得：", IG_entropy_B)

➂誤分類率による情報利得

# 親ノードの誤分類率
IGm_p = 1 - np.maximum(4/8, 1-4/8)

# 子ノードAの誤分類率
IGm_A_l = 1 - np.maximum(3/4, 1-3/4) # 左
IGm_A_r = 1 - np.maximum(1/4, 1-1/4) # 右
# 子ノードBの誤分類率
IGm_B_l = 1 - np.maximum(2/6, 1-2/6) # 左
IGm_B_r = 1 - np.maximum(2/2, 1-2/2) # 右

# 各分岐の情報利得
IG_misclass_A = IGm_p - 4/8 * IGm_A_l - 4/8 * IGm_A_r
IG_misclass_B = IGm_p - 6/8 * IGm_B_l - 2/8 * IGm_B_r
print("分岐Aの情報利得：", IG_misclass_A)
print("分岐Bの情報利得：", IG_misclass_B)

まとめ

	分類条件A	分類条件B
ジニ不純度	0.125	0.167
エントロピー	0.189	0.311
誤分類率	0.250	0.250

• ジニとエントロピーでは共に、分類条件Bの方が優先されるのは明白です。実際、結果も非常に似たものになります。
• 一方、誤分類率では、分類条件AとBがほぼ同率となっています。
• このように、誤分類率は変数間で明らかな差分をとらない傾向があることから、sklearnの決定木モデルでは、分割基準をジニとエントロピーの２つとしている（らしいです）。
• なお、ジニの方が、エントロピーのような対数の計算がない分だけ少し処理が速いかも知れませんね。