一般逆行列の初歩の初歩（その2: 連立1次方程式への応用）

※ この記事を書く際に利用したコードに関連するライブラリのバージョンは以下になります．

Python: 3.9.7
numpy:  1.20.3
matplotlib:  3.4.2

この記事で説明すること

一般逆行列の初歩の初歩（その1: イメージと計算方法）の続きです．

一般逆行列を利用して，連立1次方程式の解を求める方法について説明します（主に参考文献[1]の4.2節に基づいています）．
行列を使った連立1次方程式ぐらいの線形代数の知識があれば理解できると思います．
具体的には以下について，pythonのコードを示しながら説明します．

• 一般逆行列を使って解が無数にある連立1次方程式や，解がない連立1次方程式の それっぽい1つの解 を求める

その1の方では以下について説明しているので，よかったらご覧ください．

• 一般逆行列とはなんなのか
• 一般逆行列がどのように計算されるかの確認

連立方程式の解の個数と係数行列の関係を確認する

以下の3つの2元連立1次方程式を考えます．

(1)~\left\{
\begin{array}{l}
2x+y=1 \\
x+2y=1
\end{array}
\right.
,~ ~ ~ ~ ~ ~
(2)~\left\{
\begin{array}{l}
x+y=3 \\
2x+2y=6
\end{array}
\right.
,~ ~ ~ ~ ~ ~
(3)~\left\{
\begin{array}{l}
x+y&=&4 \\
x-y&=&0 \\
y&=&1
\end{array}
\right.
.

上の3式を行列とベクトルで以下のように表します（ $\mathbf{x}=(x, y)^T$ とおく．）．

(1)~A\mathbf{x}=b_1,~~
(2)~B\mathbf{x}=b_2,~~
(3)~C\mathbf{x}=b_3.

ここで，係数行列や定数ベクトルは以下のようにおいています．

A = \begin{bmatrix}
2 & 1 \\
1 & 2
\end{bmatrix},
B = \begin{bmatrix}
1 & 1 \\
2 & 2
\end{bmatrix},
C = \begin{bmatrix}
1 & 1 \\
1 & -1 \\
0 & 1
\end{bmatrix},\\
b_1 = \begin{bmatrix}
1  \\
1
\end{bmatrix},
b_2 = \begin{bmatrix}
3  \\
6
\end{bmatrix},
b_3 = \begin{bmatrix}
4 \\
0 \\
1
\end{bmatrix}

今回は2変数の連立方程式なので，連立方程式を構成する各式を，1本の直線の式と見てxy平面にプロットすることができます．
そこで，今回考えている3つの連立方程式をプロットしてみます（コードは付録1: プロットのためのコードを参照）．

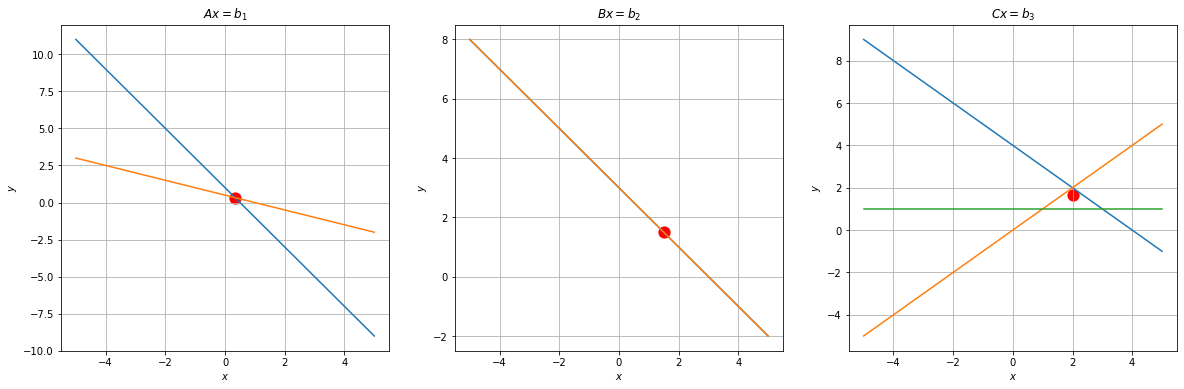
プロットした結果を見ると，

• (1)の方程式は2直線の交点がただ1つ定まるので，唯一の解を持つことがわかります．
• (2)の方程式は2直線がぴったり重なっているので，解が無数にあることがわかります（不定）．
• (3)の方程式は3直線が交わる点が存在しないので，解が存在しないことがわかります（不能）．

このような話は学部の線形代数の講義などでよく扱う内容かと思います．
しかし，今回の記事のメインは，一般逆行列を用いることで，(2)や(3)のような連立方程式に対しても，それっぽい1つの解を計算することができるということです．

一般逆行列を利用してそれっぽい答えを計算する

先に示した連立方程式(1)の係数行列 $A$ は逆行列 $A^{-1}$ が存在します．
よって，$\mathbf{x}=A^{-1}b_1$ とすれば唯一の解を求めることができます．

しかし，$B, C$ は逆行列が存在しない（$B$ は非正則で，$C$ は正方行列でない）ため，そのように解を求めることができません．
一方で，(2)や(3)のような，解が一意に定まらない連立方程式に対しても，1つの解を出してほしいことがあるようです（例．ロボットの移動制御で，次の時刻で移動する位置を1つ決めてほしい）．

そのような場合に，一般逆行列が利用できます．
その1で説明した通り，一般逆行列は逆行列の定義できない，正方でない行列や正則でない行列に対しても計算できます．
それを逆行列の代わりに用いることで，それっぽい1つの解 を求めることができます．

具体的には，$B, C$ の一般逆行列をそれぞれ $B^-, C^-$ とすると，$\mathbf{x}=B^{-}b_2$, $\mathbf{x}=C^{-}b_3$ のように計算することでそれっぽい解を計算できます（一般逆行列を用いて解を計算するコードは付録2: 一般逆行列を用いて座標を計算するコードを参照）．
実際に一般逆行列を利用して計算できた解を赤点でプロットに追加してみます．

• 一番左のプロットでは，唯一の解を計算できます．行列 $A$ に逆行列が定義できる場合は，$A$ の一般逆行列と逆行列は一致するためです．
• 真ん中のプロットでは，無数にある解の中の1つが計算されています．
• 一番右のプロットに関しては，解のない方程式ですが，橙と青線の交点に近く，緑線にも近い，それっぽい解が計算されています（3直線が交わってないので解という言葉を使うのは不適切ですが）．

"それっぽい" とは？

さっきから "それっぽい" 解といっていますが，一般逆行列を用いて計算された答えは，具体的にどのように選ばれた座標になっているのでしょうか．

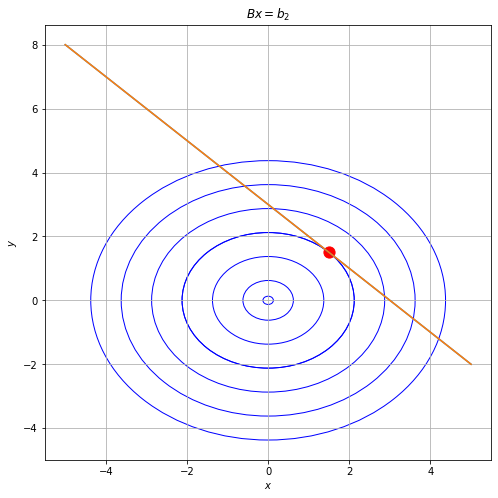
解が無数に存在する場合: 無数に存在する解の中でも，ノルム $||\mathbf{x}||^2$ が最小になる点が選ばれる．

• 解が無数に存在する場合は，なるべく原点に近い座標が "それっぽい" ということになります．
• 最適化の観点で述べると，$A\mathbf{x}=b$ を制約条件，$||\mathbf{x}||^2$ を目的関数とした最小化問題の解が，一般逆行列を利用して計算できる座標ということになります．
• 以下の図を見ると，実際にノルムが最小になる点が一般逆行列を利用することで選ばれていることがわかります（原点を中心とする円と，直線との接点になっている．）．

原点を中心とする円をつけ加えたver.

fig, ax = plt.subplots(figsize=(8, 8))
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
ax.set_title('$Bx=b_2$')
ax.scatter(sol2[0], sol2[1], s=500, marker='.', c='r')
ax.plot(x, y21)
ax.plot(x, y22)
nrm = nl.norm(sol2)
for i in range(4):
  c1 = patches.Circle(xy=(0, 0), radius=nrm+0.75*i, fill=False, ec='b')
  c2 = patches.Circle(xy=(0, 0), radius=nrm-0.75*i, fill=False, ec='b')
  ax.add_patch(c1)
  ax.add_patch(c2)
ax.grid(True)
plt.show()

解が存在しない場合: $||A\mathbf{x}-b||^2$ が最小になる点が選ばれる．

• 解が存在するということは，$A\mathbf{x}=b \leftrightarrow A\mathbf{x}-b=0$ となる $\mathbf{x}$ が存在するということなので，$||A\mathbf{x}-b||^2=0$ となる $\mathbf{x}$ が存在します．
  解がない場合は，この $||A\mathbf{x}-b||^2$ がなるべく小さい座標が "それっぽい" ということになります．
• 最適化の観点で述べると，$||A\mathbf{x}-b||^2$ を目的関数とした最小化問題の解が，一般逆行列を利用して計算できる座標ということになります．
• 本当に $||A\mathbf{x}-b||^2$ を最小化しているかを確認してみます．各座標 $\mathbf{x}$ について $||A\mathbf{x}-b||^2$ が計算できるので，平面上に $||A\mathbf{x}-b||^2$ の値の等高線を引いてみます（以下の図）．実際に，一般逆行列で求めた解である赤点の位置で $||A\mathbf{x}-b||^2$ の値が最小になっていることが確認できました．

3直線とそれっぽい解と，二乗誤差の等高線をプロットする

# Cx = b3
C = np.array([[1, 1], [1, -1], [0, 1]])
b3 = np.array((4, 0, 1))
x = np.linspace(-2, 4, 300)
y = np.linspace(-2, 4, 300)
sol3 = np.dot(nl.pinv(C), b3)

# 方程式の表す直線の式
y31 = (-C[0][0] * x + b3[0]) / C[0][1]
y32 = (-C[1][0] * x + b3[1]) / C[1][1]
y33 = (-C[2][0] * x + b3[2]) / C[2][1]

# 等高線描画用
x = np.linspace(-2, 4, 300)
y = np.linspace(-2, 4, 300)
X, Y = np.meshgrid(x, y)
# ||Cx-b3||の値を格納する
err = np.ndarray((300, 300))
for i in range(len(X)):
  for j in range(len(X)):
    # ||Cx-b3||の計算
    err[i][j] = nl.norm(np.dot(C, np.array((X[i][j], Y[i][j]))) - b3)

fig, ax = plt.subplots(figsize=(8, 8))
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
ax.set_xlim(-2, 4)
ax.set_ylim(-2, 4)
ax.set_title('$Cx=b_3$')
ax.scatter(sol3[0], sol3[1], s=500, marker='.', c='r')
ax.plot(x, y31)
ax.plot(x, y32)
ax.plot(x, y33)
cs = ax.contour(X, Y, err, cmap='Reds_r', linestyles='dashed', levels=15)
ax.clabel(cs, colors='black', fontsize=14)
ax.grid(True)
plt.show()

参考

[1] 金谷健一, これなら分かる最適化数学 ―基礎原理から計算手法まで― (共立出版), 200

付録

付録1: 直線のプロットのためのコード

3つのグラフを横に並べて表示する

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
x = np.linspace(-5, 5, 100) # [-5,5]の範囲で100点等間隔にとる

######################
# 3つの連立方程式の定義 #
######################

# Ax=b1
A = np.array([[2, 1], [1, 2]])
b1 = np.array((1,1))
# 方程式の表す直線の式
y11 = (-A[0][0] * x + b1[0]) / A[0][1]
y12 = (-A[1][0] * x + b1[1]) / A[1][1]

# Bx=b2
B = np.array([[1, 1], [2, 2]])
b2 = np.array((3,6))
# 方程式の表す直線の式
y21 = (-B[0][0] * x + b2[0]) / B[0][1]
y22 = (-B[1][0] * x + b2[1]) / B[1][1]

# Cx=b3
C = np.array([[1, 1], [1, -1], [0, 1]])
b3 = np.array((4, 0, 1))
# 方程式の表す直線の式
y31 = (-D[0][0] * x + b3[0]) / C[0][1]
y32 = (-D[1][0] * x + b3[1]) / C[1][1]
y33 = (-D[2][0] * x + b3[2]) / C[2][1]

###########################
# 定義した式たちをプロットする #
###########################

fig = plt.figure(figsize=(20,6))

# Ax=b1
ax1 = fig.add_subplot(1, 3, 1)
ax1.set_xlabel('$x$')
ax1.set_ylabel('$y$')
ax1.set_title('$Ax=b_1$')
ax1.plot(x, y11)
ax1.plot(x, y12)
ax1.grid(True)

# Bx=b2
ax2 = fig.add_subplot(1, 3, 2)
ax2.set_xlabel('$x$')
ax2.set_ylabel('$y$')
ax2.set_title('$Bx=b_2$')
ax2.plot(x, y21)
ax2.plot(x, y22)
ax2.grid(True)

# Cx=b3
ax3 = fig.add_subplot(1, 3, 3)
ax3.set_xlabel('$x$')
ax3.set_ylabel('$y$')
ax3.set_title('$Cx=b_3$')
ax3.plot(x, y31)
ax3.plot(x, y32)
ax3.plot(x, y33)
ax3.grid(True)

plt.show()

付録2: 一般逆行列を用いて座標を計算するコード

一般逆行列を用いて座標を計算するコード

nl = np.linalg
# Ax=b1の解
sol1 = np.dot(nl.inv(A), b1) # Aは正則なのでinvでもpinvでも一緒
# Bx=b2のそれっぽい座標
sol2 = np.dot(nl.pinv(B), b2)
# Cx=b3のそれっぽい座標
sol3 = np.dot(nl.pinv(C), b3)