私は、数学が好きなので今回はC言語で積分(ついでに微分)するプログラムを書いてみました。
ソースプログラム
# include<stdio.h>
int sekibunn(int x[], int bottom, int top) //定積分の計算
{
int ans, t[6] = {1, 1, 1, 1, 1, 1}, b[6] = {1, 1, 1, 1, 1, 1}, i;
t[1] = top;
b[1] = bottom;
for (i = 0; i < 2; i++) //2乗の計算
{
t[2] *= top;
b[2] *= bottom;
}
for (i = 0; i < 3; i++) //3乗の計算
{
t[3] *= top;
b[3] *= bottom;
}
for (i = 0; i < 4; i++) //4乗の計算
{
t[4] *= top;
b[4] *= bottom;
}
for (i = 0; i < 5; i++) //5乗の計算
{
t[5] *= top;
b[5] *= bottom;
}
ans = ((t[5] * x[4] / 5) + (t[4] * x[3] / 4) + (t[3] * x[2] / 3) + (t[2] * x[1] / 2) + (t[1] * x[0])) - ((b[5] * x[4] / 5) + (b[4] * x[3] / 4) + (b[3] * x[2] / 3) + (b[2] * x[1] / 2) + (b[1] * x[0]));
return ans;
}
int main(void)
{
int x[] = {0, 0, 0, 0, 0};
int i;
int or, top, bottom;
printf("整数を入力してください。\n");
for (i = 4; i >= 0; i--)
{
printf("x^%dの係数:", i);
scanf("%d", &x[i]);
}
printf("y=(%d)x^4+(%d)x^3+(%d)x^2+(%d)x+(%d)\n", x[4], x[3], x[2], x[1], x[0]);
printf("微分or定積分...1 / 0:");
scanf("%d", & or);
if (or == 0)
{
printf("範囲は?");
printf("下のほう :");
scanf("%d", &bottom);
printf("上のほう :");
scanf("%d", &top);
printf("面積は%dです。", sekibunn(x, bottom, top));
}
else if(or == 1){
printf("y=(%d)x^3+(%d)x^2+(%d)x+(%d)", x[4]*4, x[3]*3, x[2]*2, x[1]);
}
return 0;
}
結果としてはあまり正確な数字は出せませんでした。小数点以下があって整数部分が2桁以上となる数字の型が無いし、組み合わせてうまく表現する方法も思いつきませんでした。しかし、整数部分ではだいたい正しくなるように作れたのでよかったです。
実行結果(定積分)
2\int_{0}^{2}(x^4-8x^2+16)dxを計算してみました。
実際の答えが\frac{512}{15}となります。
/*整数を入力してください。
x^4の係数:2
x^3の係数:0
x^2の係数:-16
x^1の係数:0
x^0の係数:32
y=(2)x^4+(0)x^3+(-16)x^2+(0)x+(32)
微分or定積分...1 / 0:0
範囲は?下のほう :0
上のほう :2
面積は34です。*/
512/15は34.13333となるのでだいたい正しくなりました。
(微分)
y=x^4+4x^3+4x^2-1を微分せよ。実際の答えはy'=4x^3+12x^2+8xです。
/*整数を入力してください。
x^4の係数:1
x^3の係数:4
x^2の係数:4
x^1の係数:0
x^0の係数:-1
y=(1)x^4+(4)x^3+(4)x^2+(0)x+(-1)
微分or定積分...1 / 0:1
微分結果
y'=(4)x^3+(12)x^2+(8)x+(0)*/
とこんな感じになりました。
感想
次に書く機会があれば、分数を表せるような仕組みを考えたいと思います。
おまけ
# include <stdio.h>
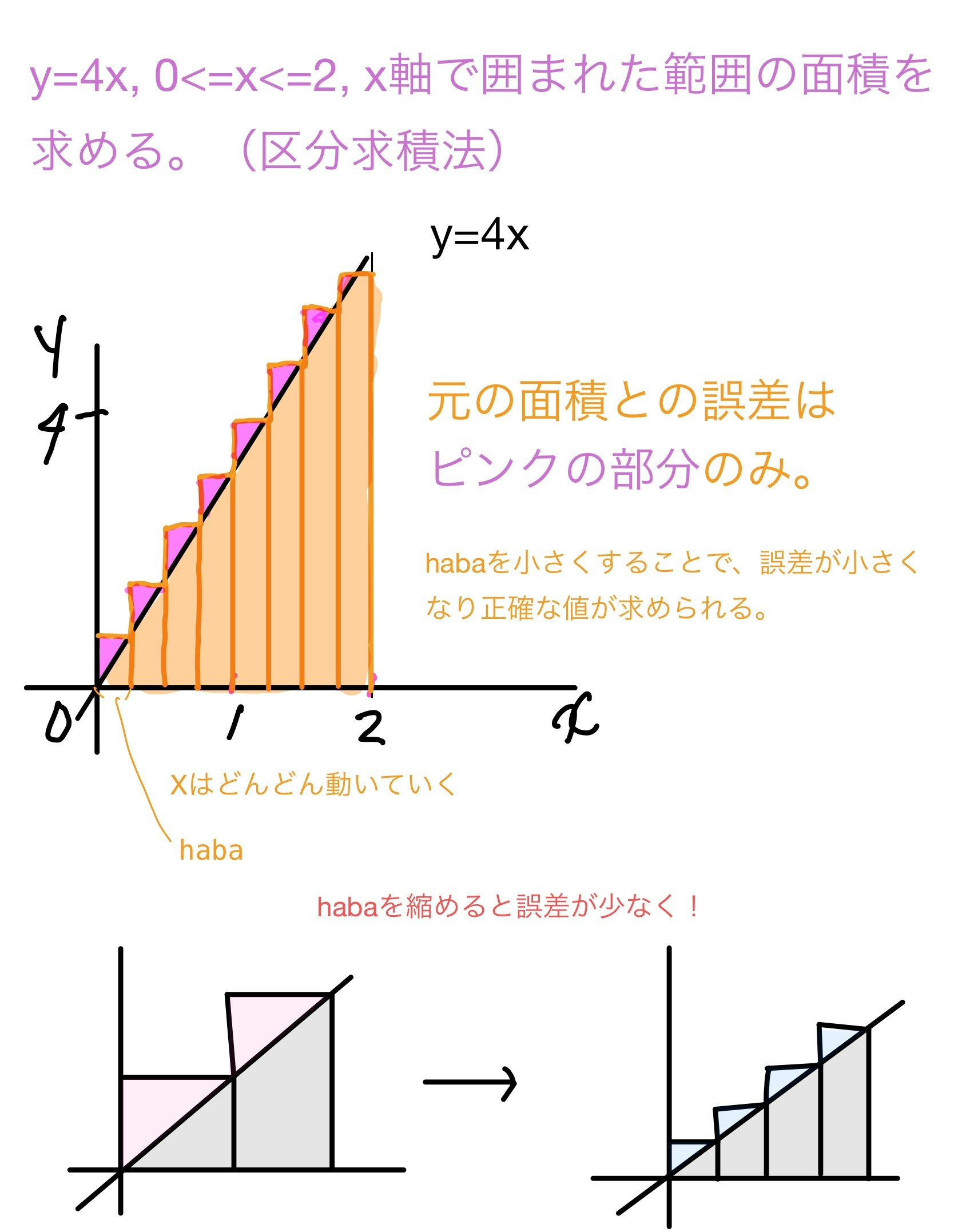
//方程式とx軸,xの範囲で囲まれた面積を近似で出すことができる。
int main(void)
{
//今回の場合y=4xで範囲は0~2
double y = 0, x, s = 0, haba = 0.001;
int i, n = (2 / haba);
x = haba;
for (i = 0; i < n; i++)
{
y = 4 * x;
printf("y=%f\n", y);
s += haba * y;
printf("面積=%f\n", s);
x += haba;
printf("x=%f\n\n", x);
}
printf("面積=%f", s);
return 0;
}
単なる思い付きだったのですが、区分求積法も再現したら本当に近似値が出るのかと思って試してみました。
xの値、求める範囲の”n=(2/n)”の2を変えると好きな範囲でできるので、もしよかったら遊んでみてください。ちなみにhabaを小さくし過ぎるとめっちゃ時間がかかります。