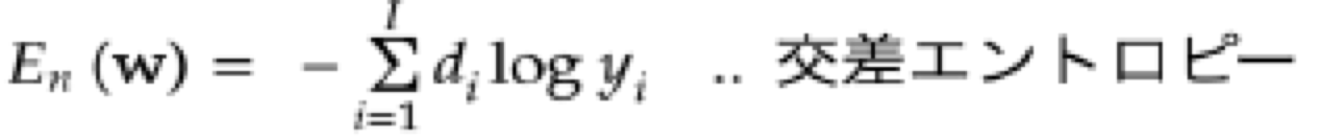要約レポート
応用数学
線形代数学:
スカラー(大きさ)とベクトル(大きさと方向)の違いから行列の特徴・計算について学習。ニューラルネットワークの重みを微分して更新する際、一気に全ての枝に対する重みを計算するために行列を用いると理解。固有値固有ベクトルは、あるベクトルをスカラーのように定数倍として扱うことができる。正方形ベクトル以外のベクトルは特異値分解をかける。特異値を取り出す(削る?)ことで画像データの情報量削減等に利用している。
統計学:
統計の要素の取り扱いについてを学習。データの整理・前処理の際に特に必要な概念と考える。ベイズ則は結果に対する原因がどこからきているか(講義動画での子供の笑顔の要因)を推定し、種々ある条件を踏まえた条件付き確率を計算する。
情報科学:どう情報を数量化して扱うか。変化量をフェアに扱う方法について。
・自己情報量
情報の変化は比率で捉えられるため、比率として表現した1/Wの積分、logで書き表すことができる。事象の珍しさWは確率Pとして置き換えることができるため以下式によって表すことができる。
自己情報量I(x)=log(W(x))=-log(P(x))
・自己情報量の期待値:シャノンエントロピー
自己情報量の平均で求めることができる。
修了問題より補足:ベルヌーイ分布分散導出の証明
ベルヌーイ分布は確率変数として0か1しかとらない。
確率変数x=1:μ
確率変数x=0:1—μ
そのため期待値E(x)は
E(x)=
=0×(1—μ)+1×μ
=μ
分散の導出
E(x2)=
=02×(1—μ)+12×μ
=μ
分散
V(x)=E(x2)-(E(x))2
=μ(1—μ)
=μ—μ2
機械学習
線形回帰モデル
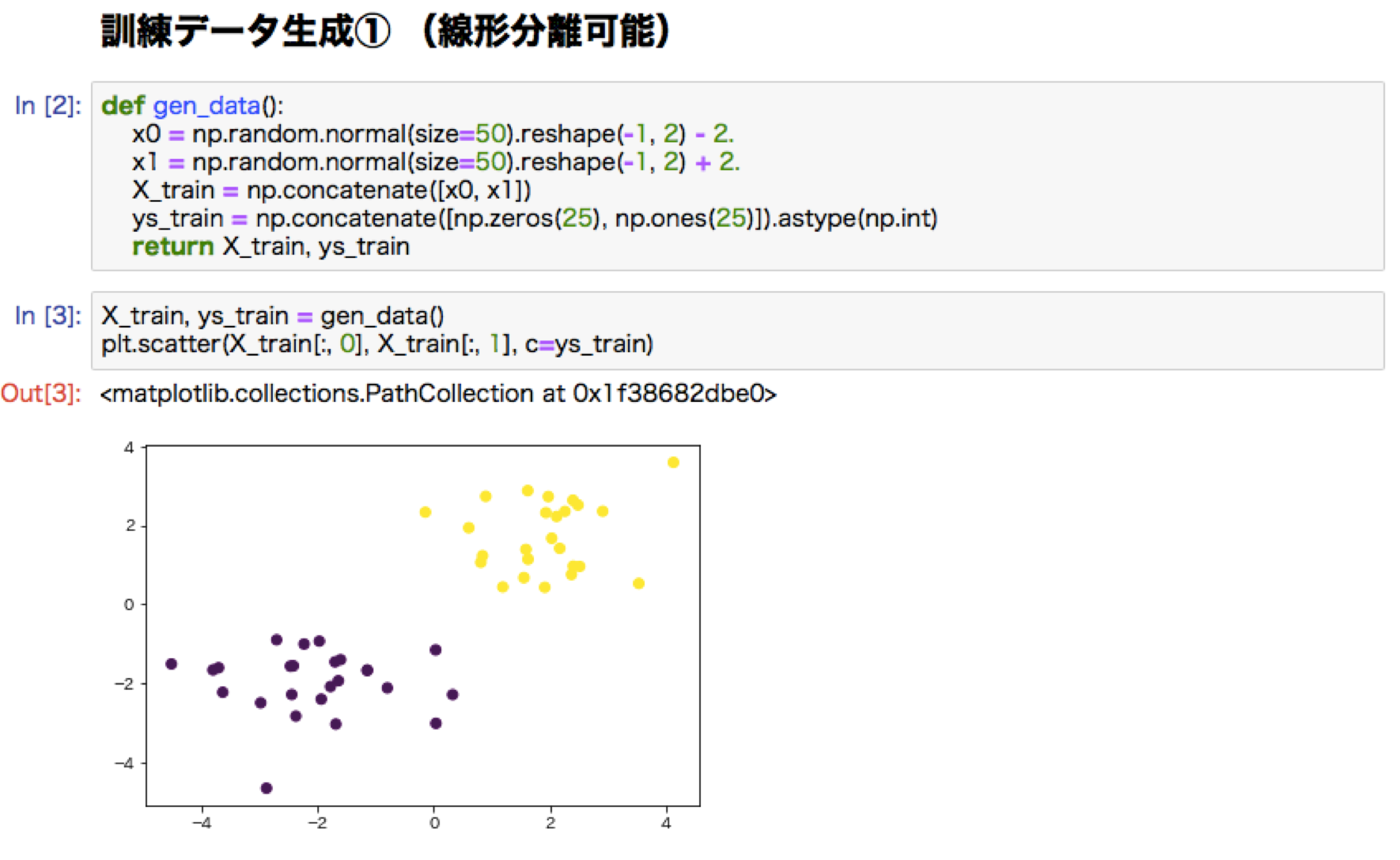
教師あり学習の一つ。入力値とm次元パラメータの線形結合を出力するモデル。モデルのパラメータは特徴量が予測値に対してどのように影響を与えるかを決定する重み。説明変数が多次元の場合、線形重回帰モデルとなる。モデルを作るため学習用データとできたモデルを検証するテストデータに分ける。今あるデータをよく説明できるモデルではなく、新しいデータに汎化するモデルを作るのが目的。
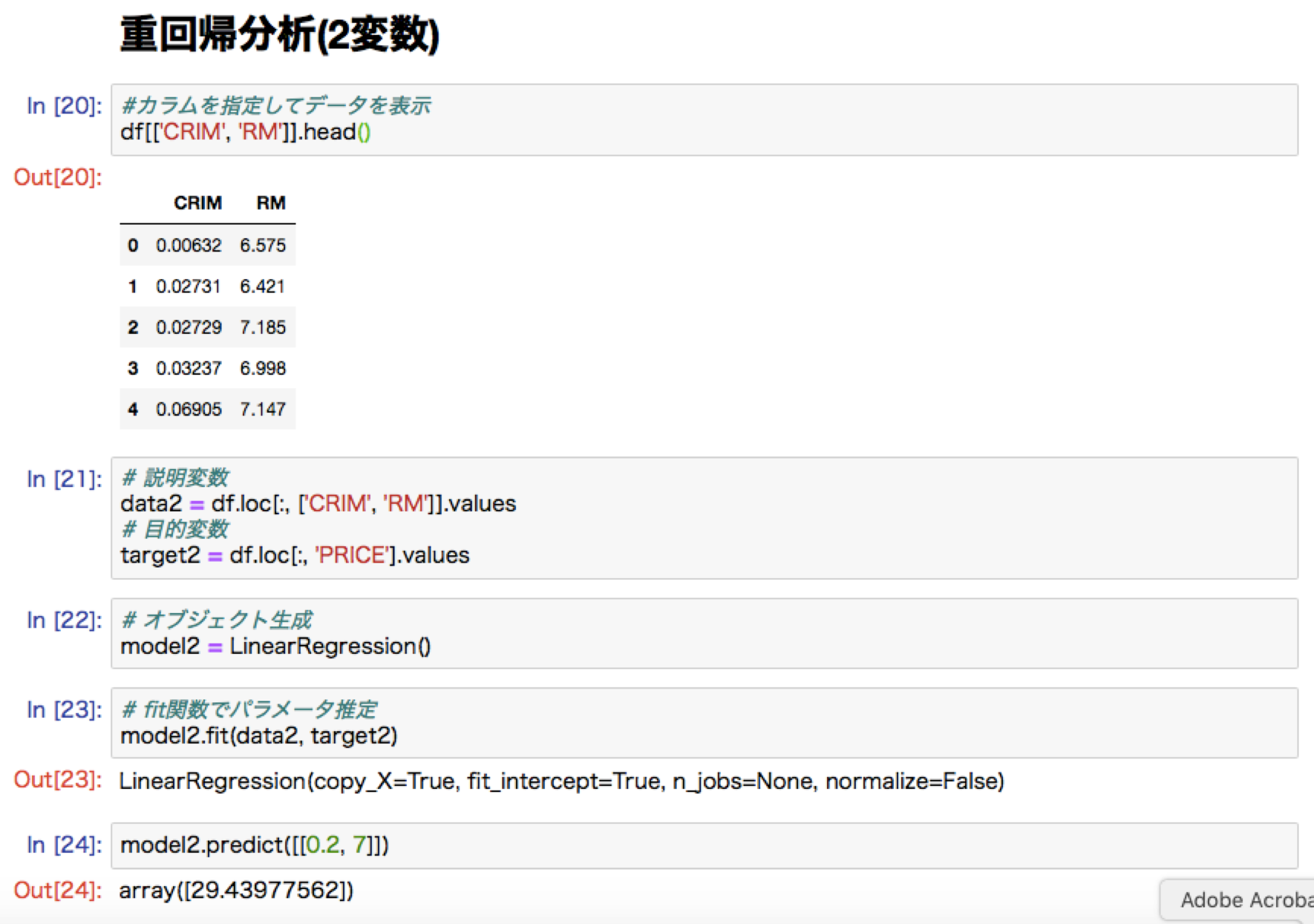
線形回帰ハンズオン:ボストンの住宅価格予測
修了試験より
・リッジ回帰:正則化係数を十分に大きくすると、いくつかの回帰係数は0に近づくが、完全に0とはならない。
・ラッソ回帰:正則化係数を十分に大きくすると、いくつかの回帰係数は完全に0となる。
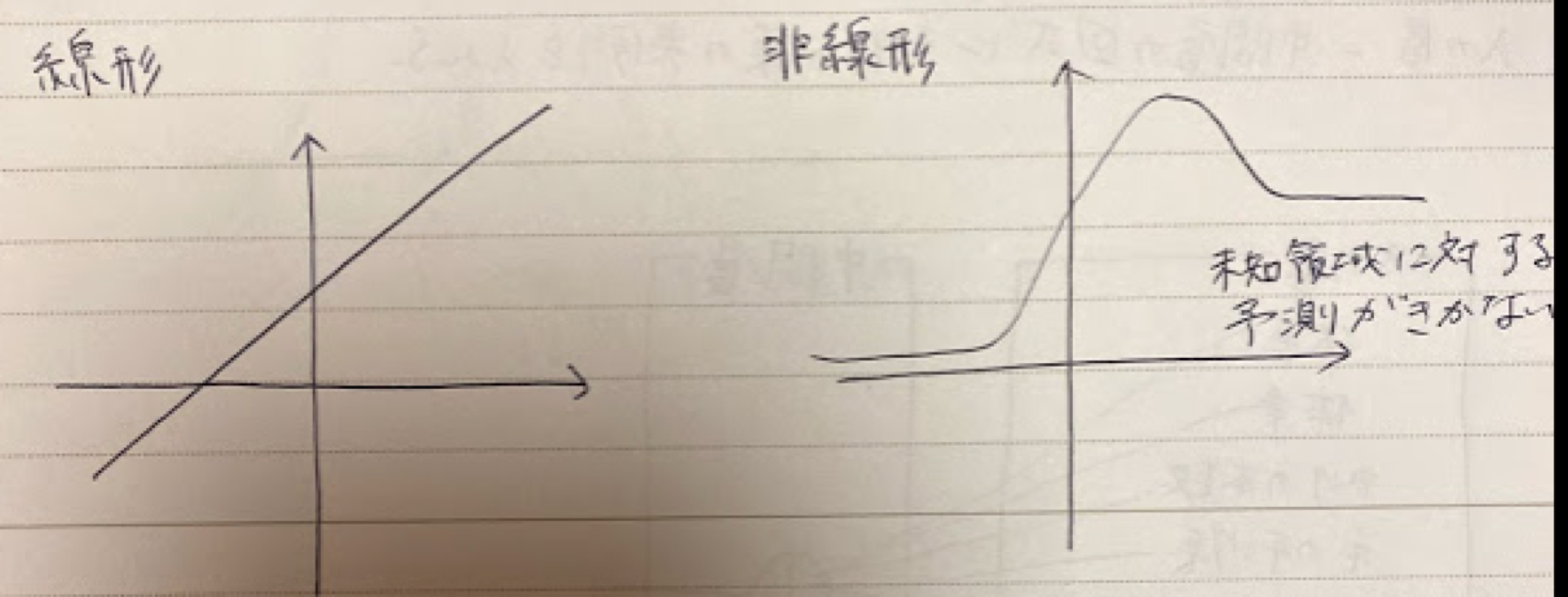
非線形回帰モデル
データ構造を線形に捉えきれない場合に適用させる。(一般的に外挿予測はできないとされている)。少ないデータでは、未学習・過学習の問題が起きやすい。モデルの複雑化に伴って正則化を行いペナルティを課して過学習を防ぐ(ただし正則化を行い過ぎると未学習となるため、過学習とはトレードオフ)。
モデル選択は以下の二つの方法で行われる
・クロスバリデーション
・ホールドアウト法:データ数が少ない時はこちらが向いている
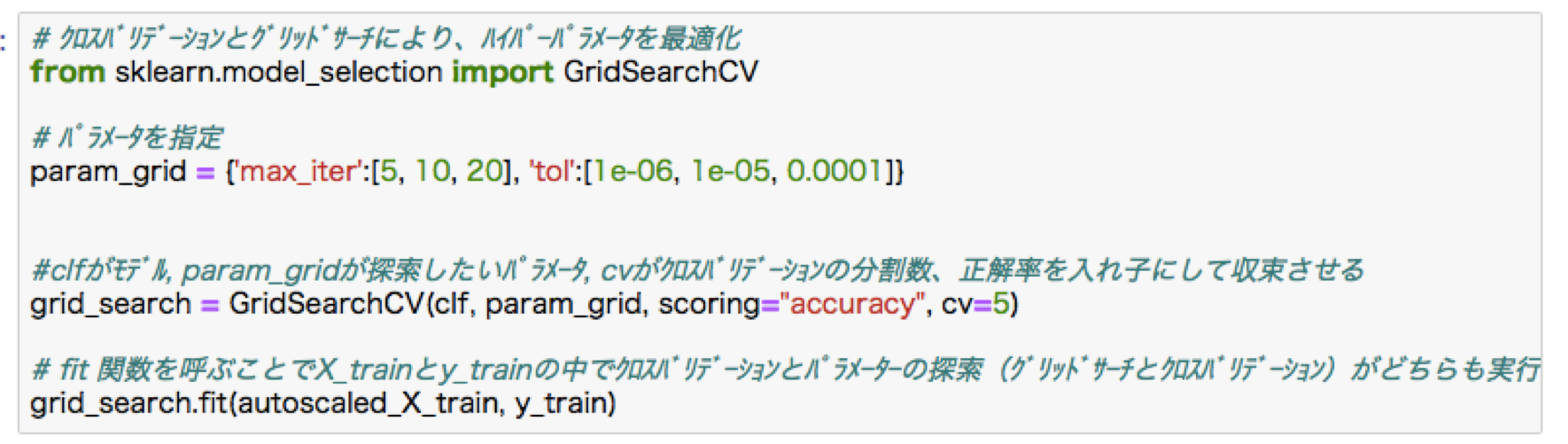
ロジステック回帰モデル
分類モデル。教師あり学習の一つ。入力した特徴量に対し、出力は連続値ではなくy or n, 0 or 1,猫?犬?, iris品種など。ベルヌーイ分布により説明される。
・最尤推定:
尤もらしさを表す尤度関数を最大化させるような推定方法
・勾配降下法:
反復学習によりパラメータを逐次更新していく方法。パラメータの微分が0になる値を解析的に求められる線形回帰モデルとは異なり、ロジステック回帰の最尤法では解析的に求めることができないためこの方法を用いる。
・確率的勾配降下法:
全てのデータを使うのではなく、計算コストを抑えるため、ランダムに抽出したものでパラメータを更新する方法。
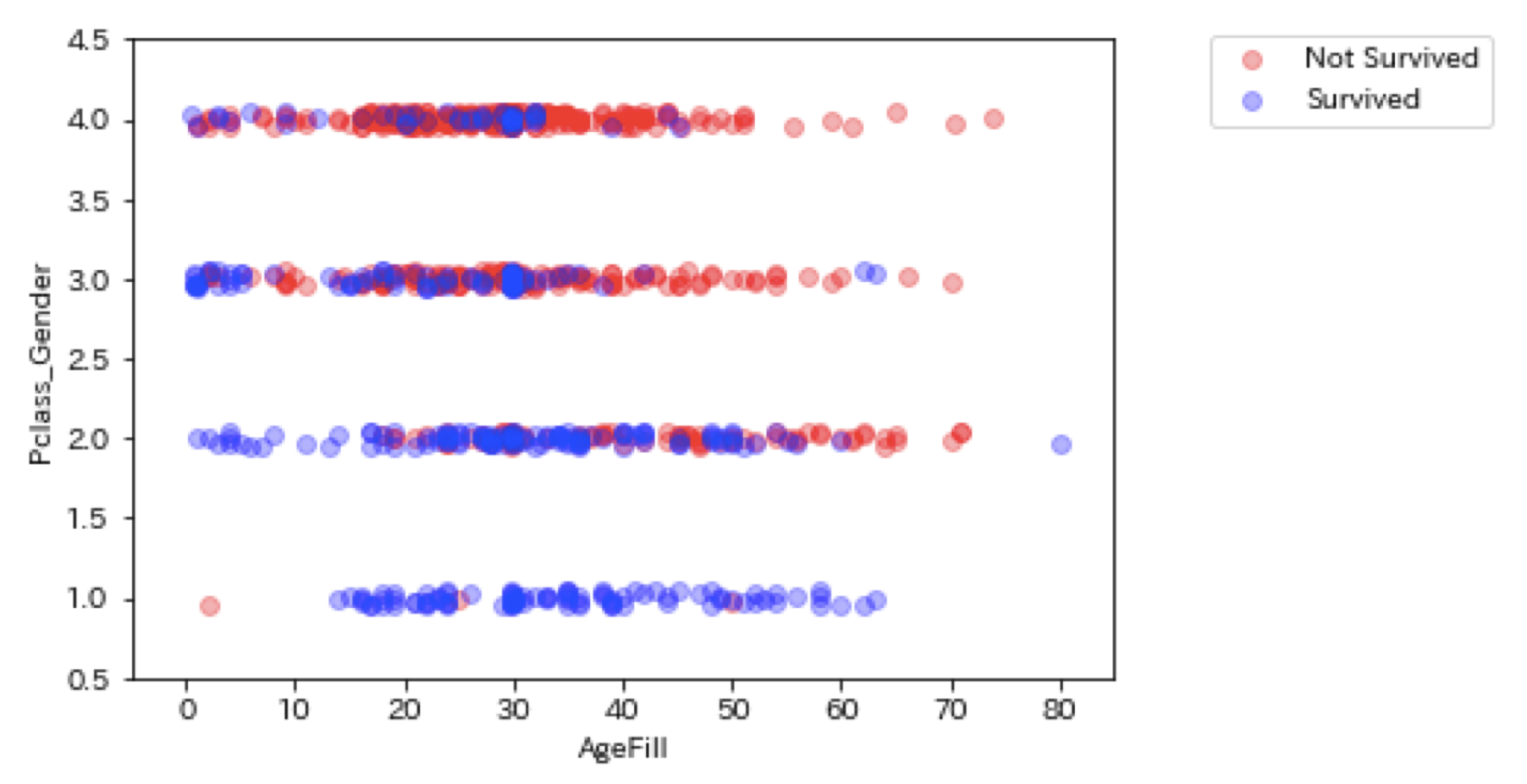
ロジステック回帰ハンズオン:タイタニック乗客生存予測
今回のプログラムでは、欠損値は平均で補完。
#チケット価格$61では生存不可。$62の生存可否と確率を表示。
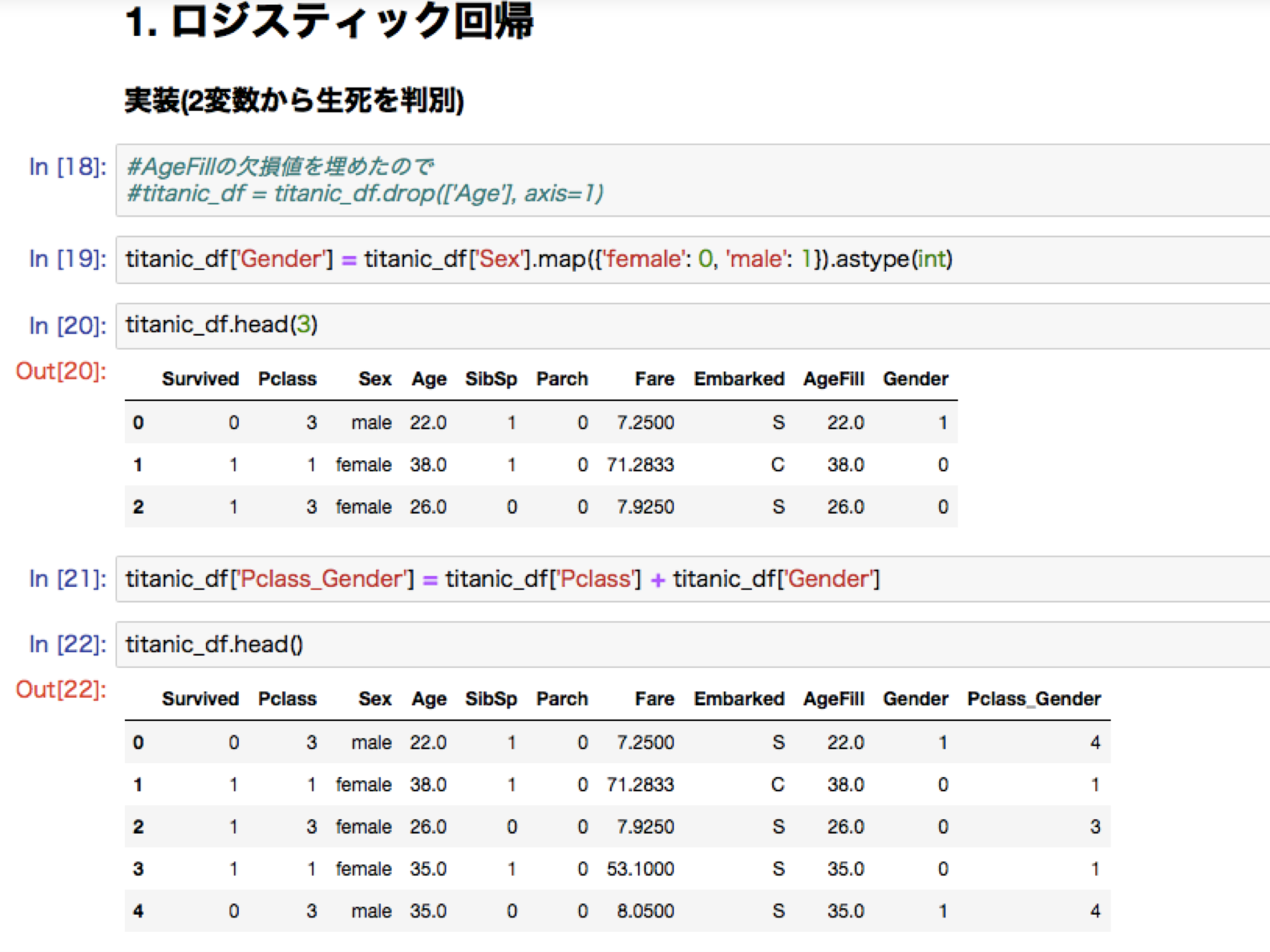
Pclass_Genderという新しい特徴量を作る。性別と階級が重要であるという知見からこの二つを重要視。実際の現場でもこのような知見が重要となる。
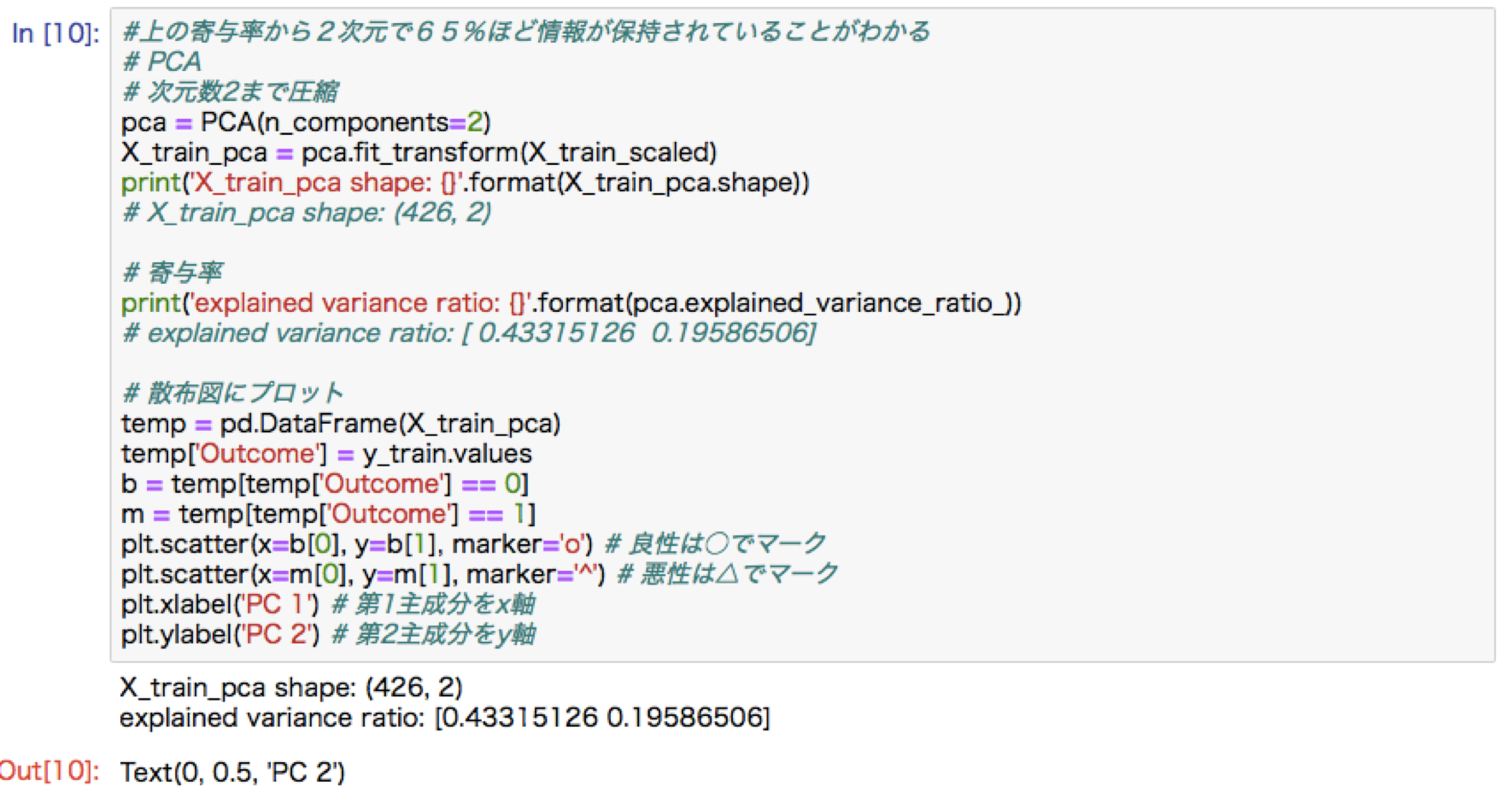
主成分分析
多次元の特徴量について情報量を抑えて低次元に落とし込む考え方。第一主成分はデータの分散が最も大きくなる軸をとる。制約条件を設けて(ノルムを1)目的関数を最大化させるような目的関数を求める。元のデータの分散共分散行列の固有値と固有ベクトルを求めることに他ならない。
アルゴリズム
分類手法
・k-nn法:最近傍のデータをk個(奇数)とり、どちらに分類されているデータが多いかで比較し、多数決により分類を決定する方法。k(チューニングパラメータ)の値を変化させることで答えは変わる。kが大きいほど分類の境界は滑らかになる。
k=3
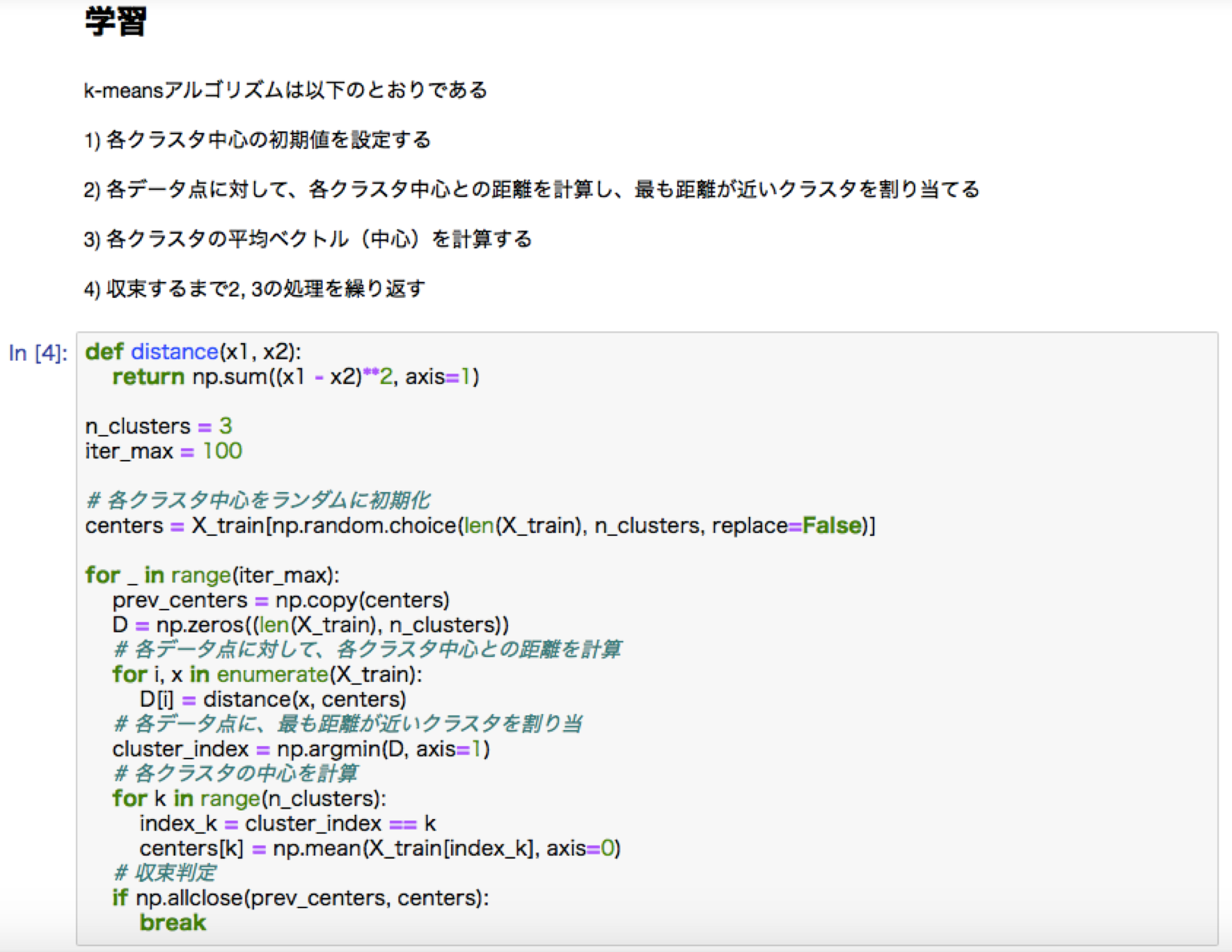
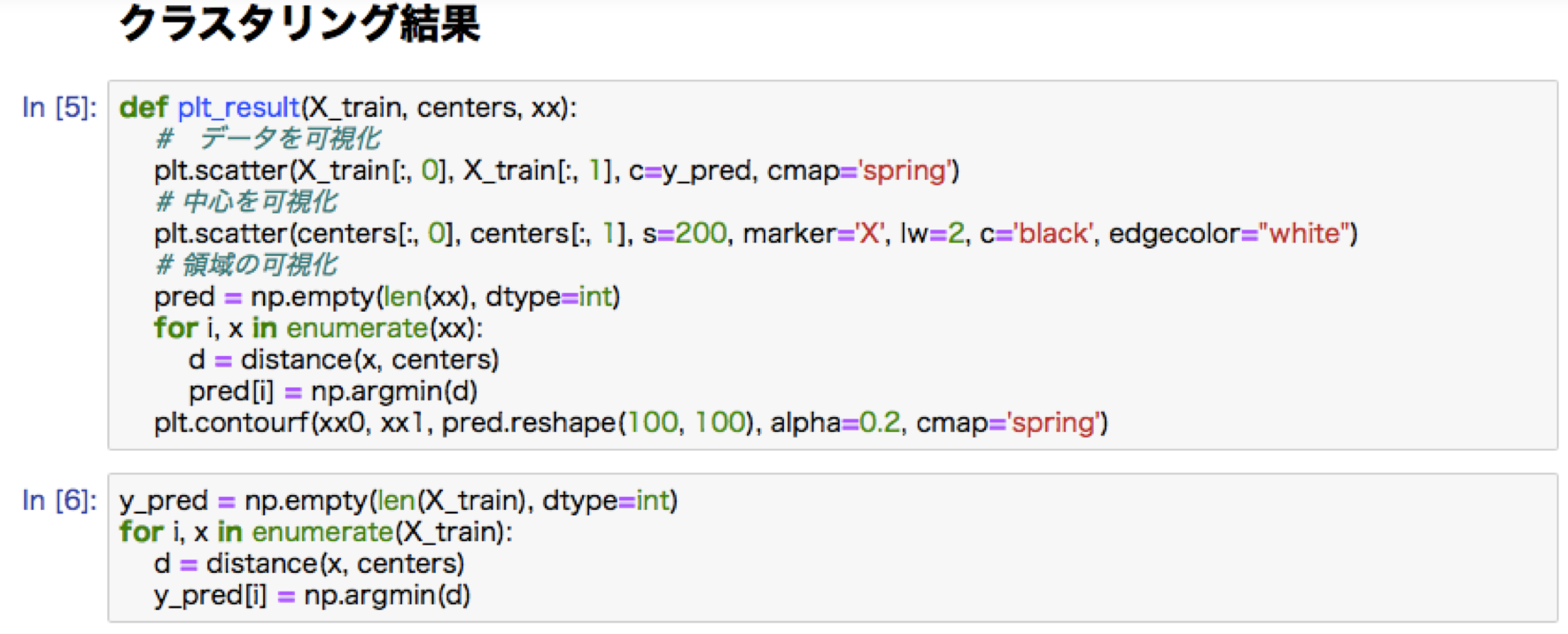
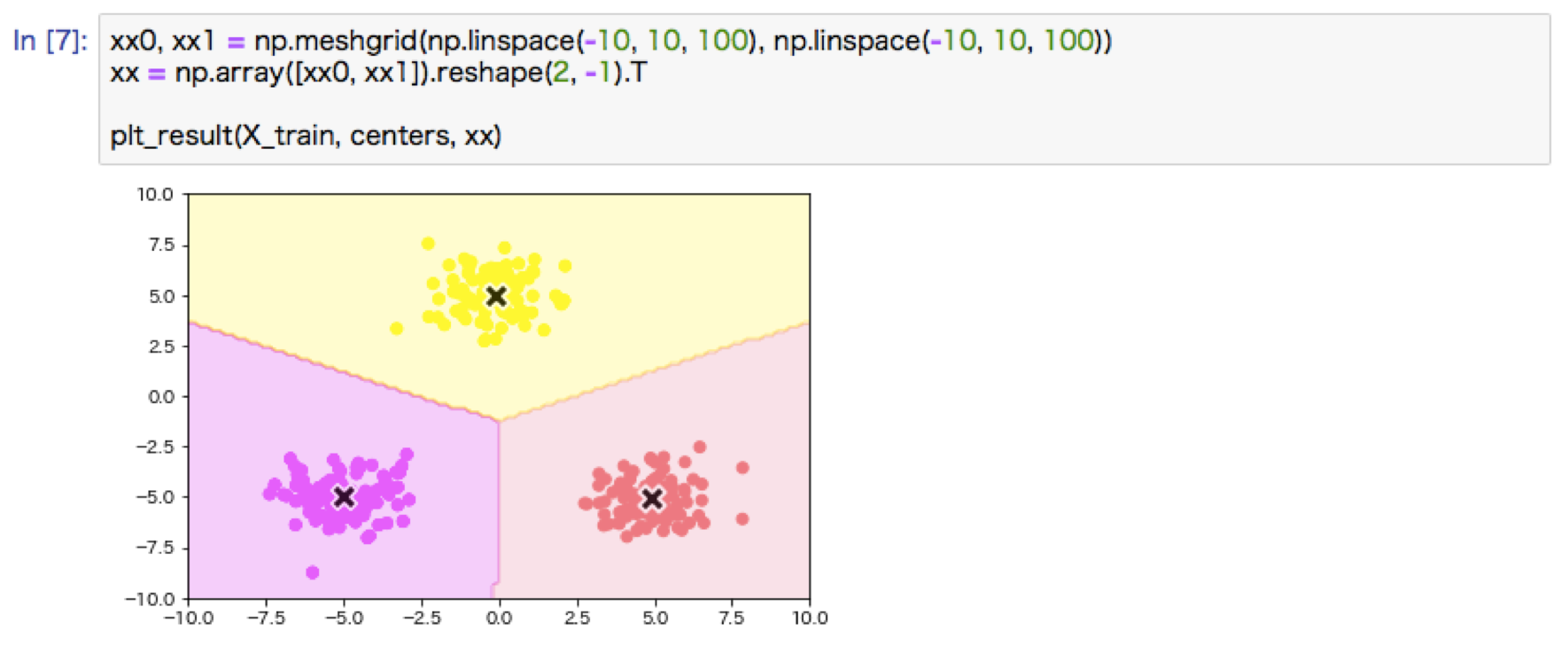
・k-means:教師なし学習。クラス分けの手法。クラスタの中心を決定し、そこからの距離し、最も距離の遠いところを新しく別のクラスタとして、再度その中心からの距離を計算していく。中心の更新を行っていくことで最終的にグループが決定される。初期値の設定が効率を左右する。
k-meansハンズオン
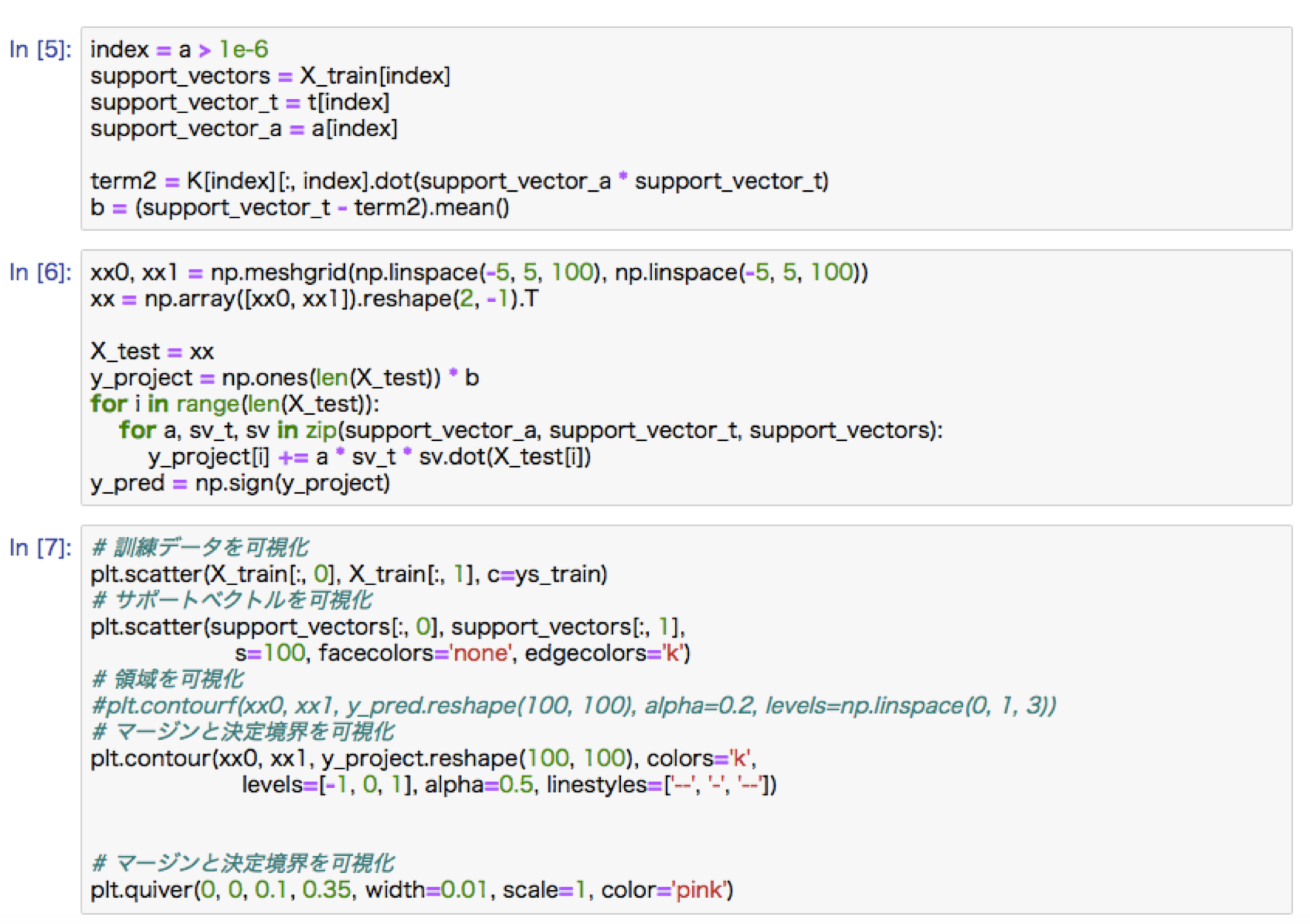
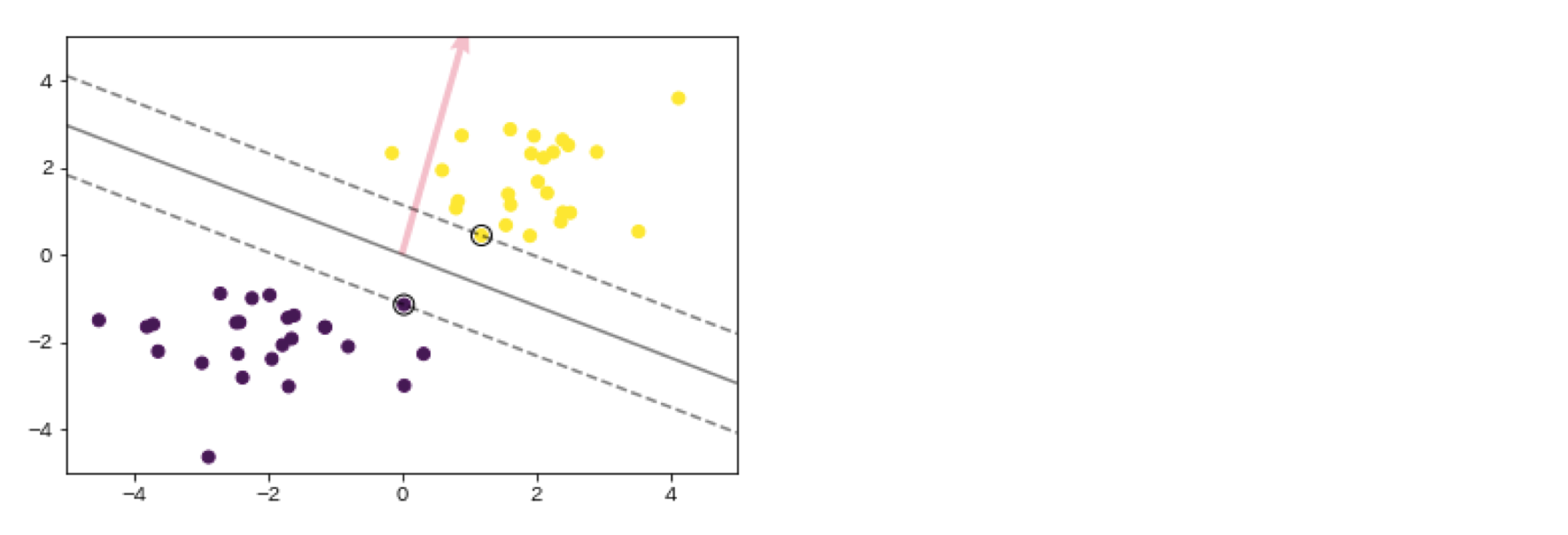
サポートベクターマシン
2クラス分類のための機械学習手法。線形判別関数と最も近いデータとの距離をマージンといい、そのマージンが最大となる線形判別関数を求める。モデルの決定にはサポートベクター(最も境界から近いデータ)のみを必要とする。サンプルをうまく分離できないときは誤差として許容し、ペナルティを課す。
深層学習前編1
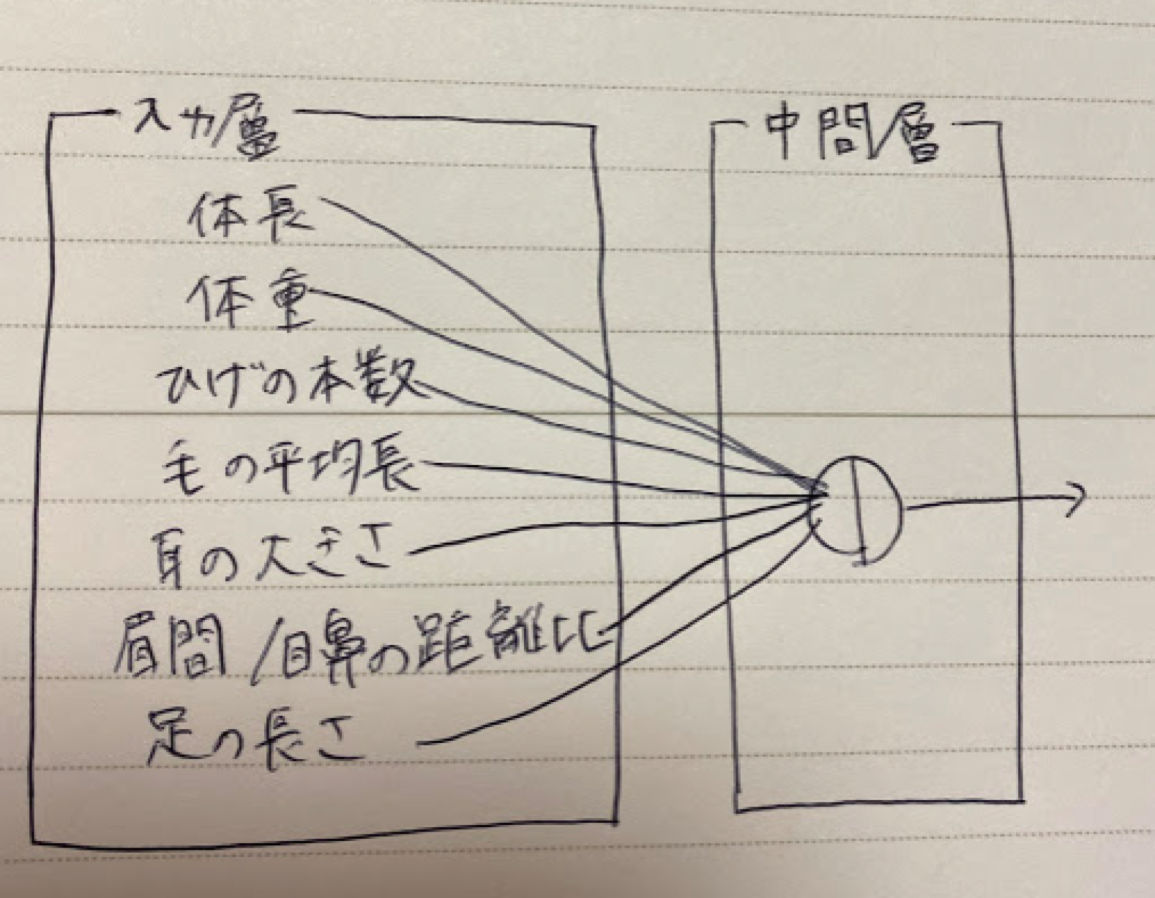
Section1:入力層—中間層
ディープラーニングの目的はニューラルネットワークの重みパレメータとバイアスの最適化。ニューラルネットワークは回帰にも分類にも対応。入力層からは各特徴に対しそれぞれ重みをかけバイアスを考慮した情報が中間層へ入力される。
Section2:活性化関数
ニューラルネットワークに対して次の層への出力の大きさを決める非線形関数。入力値の値で次の層への信号の大きさ、on/offを定める働きを持つ。中間層の活性化関数には以下がある。
・ステップ関数
しきい値を超えたら発火する関数で出力は常に1か0。パーセプトロン(ニューラルネットワークの前身)で利用された関数。0 -1間の間を表現できず、線形分離可能なものにしか対応できない。
・シグモイド関数
0 ~ 1の間を変化する関数。状態に対し、信号の強弱を伝えられるが、大きな値では出力の変化が微小なため、勾配消失問題を引き起こす事がある。
・RELU関数
現在最も使われている活性化関数。勾配消失問題の回避とスパース化に貢献することで良い成果をもたらす。
RELU関数で出力
Section3:出力層
出力層=目視できる結果となるためクライアントとしては最も重要な層になる。モデルの調整として、答えのある訓練データを学習させ、最終的な算出された出力確率と答えを比べ誤差を考慮し誤差関数を最小化させるようなモデルを更新していく。
確認テスト:二乗誤差について、なぜ引き算ではなく二乗するか述べよ
→値を正で扱うため。
確認テスト:下式二乗誤差関数の1/2が何を意味するのか述べよ
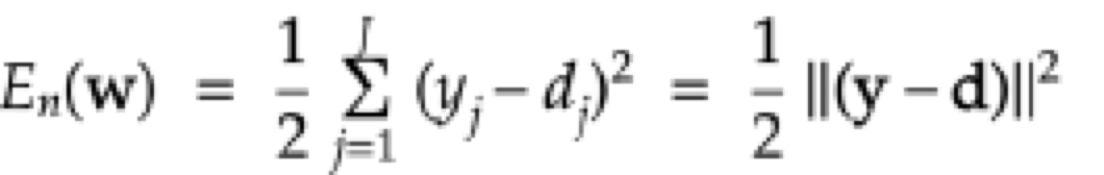
→微分の簡略化のため
出力層の活性化関数
出力層では、信号の大きさはそのままで変換させる必要があるため、中間層の活性化関数とは異なる。使用される活性化関数には以下がある。
・ソフトマックス関数:誤差関数は交差エントロピー
・恒等写像:誤差関数には二乗誤差が対応
・シグモイド関数(ロジスティック関数):誤差関数は交差エントロピー
確認テスト:ソフトマックス関数について数式のソースコードを説明せよ
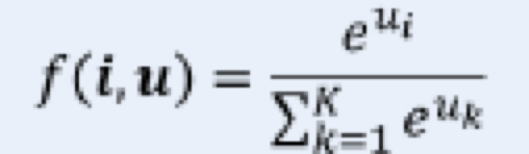
def softmax(x):
if x.ndim == 2: (次元数2)
x = x.T (受け取った値を転置)
x = x - np.max(x, axis=0) (転置した値の中のmax値を減算)
y = np.exp(x) / np.sum(np.exp(x), axis=0) (yが左辺、np.exp(x)が右辺分子、
np.sum(np.exp(x)が右辺分母)
return y.T
def cross_entropy_error(d, y):
if y.ndim == 1:
d = d.reshape(1, d.size)
y = y.reshape(1, y.size)
教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
if d.size == y.size:
d = d.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size (右辺:1e-7は影響のない微小な値を与えて分母が0にならないようにしている)
Section4:勾配降下法
深層学習の最終目的であるパラメータの最適化(誤差を最小化する)の際、一回のパラメータの更新に全てのデータを利用する。方法は以下。学習率εが大きすぎると発散してしまい最小値にたどり着かない。一方で学習率が小さすぎる場合収束するまでに時間がかかったり局所解に陥るため、εは調整が必要。
・勾配降下法
収束のためのアルゴリズム:Momentum, AdaGrad, Adadelta, Adam
・確率的勾配降下法:ランダムに抽出して計算するためコストを削減できる。オンライン学習ができる。
・ミニバッチ降下法:ランダム採取したデータの集合(ミニバッチ)の平均誤差を扱う。
確認テスト:勾配降下法の更新式に該当するソースコードは?
w(t+1)=w(t)-ε∇E
network[key] -= learning_rate * grad[key]
→どう計算するか
一般的な方法:プログラムで微小な数値を生成し擬似的に微分を計算する。
各パラメータそれぞれに対し計算するため、順伝播の計算を繰り返し行う必要があるためコストが高い。誤差逆伝播法(後述)を使う方法がリソースを減らせる。
確認テスト:オンライン学習とは何か
リアルタイムでデータが集まった際、全てのデータを計算し直すのではなく、新しいデータだけを学習させて結果を更新する方法のこと。
確認テスト:ミニバッチ後下法の更新式について以下の数式の意味を図式せよ
w(t+1)=w(t)-ε∇Et
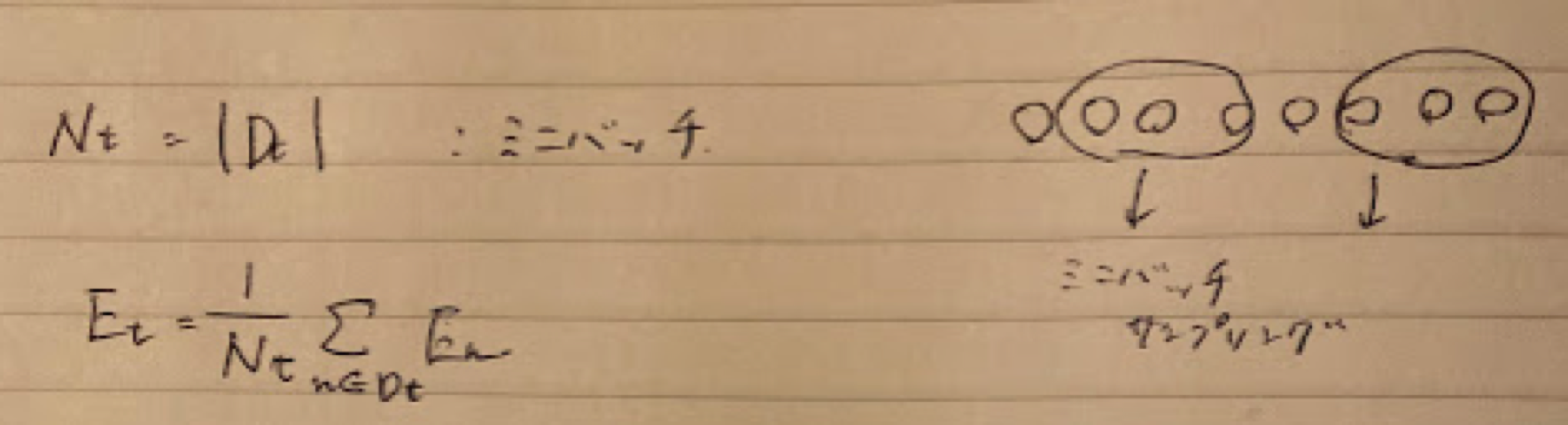
Section5:誤差逆伝播法
誤差勾配∇Eの計算法の一つ。算出された誤差を、出力層側から順に微分し、前の層に伝播していく。最小限の計算で各パラメータでの微分値を解析的に計算する手法。計算結果から微分を逆算していくことで不要な再帰的計算を避けることができる。
確認テスト:誤差逆伝播法では不要な再帰的処理を避ける事が出来る。既に行った計算結果を保持しているソースコードを抽出せよ。
誤差逆伝播
def backward(x, d, z1, y):
print("##### 誤差逆伝播開始 #####")
grad = {}
W1, W2 = network['W1'], network['W2']
b1, b2 = network['b1'], network['b2']
# 出力層でのデルタ
delta2 = functions.d_sigmoid_with_loss(d, y)#シグモイド関数とクロスエントロピーの複合関数の導関数の値を求める。
# b2の勾配
grad['b2'] = np.sum(delta2, axis=0)
# W2の勾配
grad['W2'] = np.dot(z1.T, delta2)
# 中間層でのデルタ
delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1)
# b1の勾配
grad['b1'] = np.sum(delta1, axis=0)
# W1の勾配
grad['W1'] = np.dot(x.T, delta1)
確認テスト:2つの空欄に該当するソースコードを示せ。
delta2 = functions.d_mean_squared_error(d, y)
grad['W2'] = np.dot(z1.T, delta2)
実装演習課題
1_2_back_propagation 2019/12/12 20'25
In [1]: import sys, os
sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするため
の設定
import numpy as np
from common import functions
import matplotlib.pyplot as plt
def print_vec(text, vec):
print("*** " + text + " ***")
print(vec)
print("shape: " + str(x.shape))
print("")
In [7]: # ウェイトとバイアスを設定
ネートワークを作成
def init_network():
print("##### ネットワークの初期化 #####")
network = {}
network['W1'] = np.array([
[0.1, 0.3, 0.5],
[0.2, 0.4, 0.6]
])
network['W2'] = np.array([
[0.1, 0.4],
[0.2, 0.5],
[0.3, 0.6]
])
network['b1'] = np.array([0.1, 0.2, 0.3])
network['b2'] = np.array([0.1, 0.2])
print_vec("重み1", network['W1'])
print_vec("重み2", network['W2'])
print_vec("バイアス1", network['b1'])
print_vec("バイアス2", network['b2'])
return network
順伝播
def forward(network, x):
print("##### 順伝播開始 #####")
W1, W2 = network['W1'], network['W2']
b1, b2 = network['b1'], network['b2']
u1 = np.dot(x, W1) + b1
z1 = functions.relu(u1)
u2 = np.dot(z1, W2) + b2
y = functions.softmax(u2)
1_2_back_propagation 2019/12/12 20'25
http://localhost:8890/nbconvert/html/Desktop/AI試験/DNN_code/lesson_1/1_2_back_propagation.ipynb?download=false 2 / 4 ページ
print_vec("総入力1", u1)
print_vec("中間層出力1", z1)
print_vec("総入力2", u2)
print_vec("出力1", y)
print("出力合計: " + str(np.sum(y)))
return y, z1
誤差逆伝播
def backward(x, d, z1, y):
print("\n##### 誤差逆伝播開始 #####")
grad = {}
W1, W2 = network['W1'], network['W2']
b1, b2 = network['b1'], network['b2']
出力層でのデルタ
delta2 = functions.d_sigmoid_with_loss(d, y)
b2の勾配
grad['b2'] = np.sum(delta2, axis=0)
W2の勾配
grad['W2'] = np.dot(z1.T, delta2)
中間層でのデルタ
delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1)
b1の勾配
grad['b1'] = np.sum(delta1, axis=0)
W1の勾配
grad['W1'] = np.dot(x.T, delta1)
print_vec("偏微分_dE/du2", delta2)
print_vec("偏微分_dE/du2", delta1)
print_vec("偏微分_重み1", grad["W1"])
print_vec("偏微分_重み2", grad["W2"])
print_vec("偏微分_バイアス1", grad["b1"])
print_vec("偏微分_バイアス2", grad["b2"])
return grad
訓練データ
x = np.array([[1.0, 5.0]])
目標出力
d = np.array([[0, 1]])
学習率
learning_rate = 0.01
network = init_network()
y, z1 = forward(network, x)
誤差
loss = functions.cross_entropy_error(d, y)
grad = backward(x, d, z1, y)
誤差をパラメータで微分
1_2_back_propagation 2019/12/12 20'25
http://localhost:8890/nbconvert/html/Desktop/AI試験/DNN_code/lesson_1/1_2_back_propagation.ipynb?download=false 3 / 4 ページ
for key in ('W1', 'W2', 'b1', 'b2'):
network[key] -= learning_rate*grad[key]
学習率*パラメータの勾配
print("##### 結果表示 #####")
print("##### 更新後パラメータ #####")
print_vec("重み1", network['W1'])
print_vec("重み2", network['W2'])
print_vec("バイアス1", network['b1'])
print_vec("バイアス2", network['b2'])
ネットワークの初期化
*** 重み1 ***
[[0.1 0.3 0.5]
[0.2 0.4 0.6]]
*** 重み2 ***
[[0.1 0.4]
[0.2 0.5]
[0.3 0.6]]
*** バイアス1 ***
[0.1 0.2 0.3]
*** バイアス2 ***
[0.1 0.2]
順伝播開始
*** 総入力1 ***
[[1.2 2.5 3.8]]
*** 中間層出力1 ***
[[1.2 2.5 3.8]]
*** 総入力2 ***
[[1.86 4.21]]
*** 出力1 ***
[[0.08706577 0.91293423]]
出力合計: 1.0
誤差逆伝播開始
*** 偏微分_dE/du2 ***
[[ 0.08706577 -0.08706577]]
*** 偏微分_dE/du2 ***
[[-0.02611973 -0.02611973 -0.02611973]]
*** 偏微分_重み1 ***
[[-0.02611973 -0.02611973 -0.02611973]
[-0.13059866 -0.13059866 -0.13059866]]
1_2_back_propagation 2019/12/12 20'25
http://localhost:8890/nbconvert/html/Desktop/AI試験/DNN_code/lesson_1/1_2_back_propagation.ipynb?download=false 4 / 4 ページ
In [ ]:
*** 偏微分_重み2 ***
[[ 0.10447893 -0.10447893]
[ 0.21766443 -0.21766443]
[ 0.33084994 -0.33084994]]
*** 偏微分_バイアス1 ***
[-0.02611973 -0.02611973 -0.02611973]
*** 偏微分_バイアス2 ***
[ 0.08706577 -0.08706577]
結果表示
更新後パラメータ
*** 重み1 ***
[[0.1002612 0.3002612 0.5002612 ]
[0.20130599 0.40130599 0.60130599]]
*** 重み2 ***
[[0.09895521 0.40104479]
[0.19782336 0.50217664]
[0.2966915 0.6033085 ]]
*** バイアス1 ***
[0.1002612 0.2002612 0.3002612]
*** バイアス2 ***
[0.09912934 0.20087066]
途中の確認テスト等で説明や図示があったため、実際のコードがどこに対応するのか確認することができた。
確率勾配降下法
import sys, os
sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするため
の設定
import numpy as np
from common import functions
import matplotlib.pyplot as plt
def print_vec(text, vec):
print("*** " + text + " ***")
print(vec)
print("shape: " + str(x.shape))
print("")
In [2]: # サンプルとする関数
yの値を予想するAI
def f(x):
y = 3 * x[0] + 2 * x[1]
return y
初期設定
def init_network():
print("##### ネットワークの初期化 #####")
network = {}
nodesNum = 10
network['W1'] = np.random.randn(2, nodesNum)
network['W2'] = np.random.randn(nodesNum)
network['b1'] = np.random.randn(nodesNum)
network['b2'] = np.random.randn()
print_vec("重み1", network['W1'])
print_vec("重み2", network['W2'])
print_vec("バイアス1", network['b1'])
print_vec("バイアス2", network['b2'])
return network
1_3copy 2019/12/12 20'26
http://localhost:8890/nbconvert/html/Desktop/AI試験/DNN_code/lesson_1/1_3copy.ipynb?download=false 2 / 4 ページ
In [9]: # 順伝播
def forward(network, x):
print("##### 順伝播開始 #####")
W1, W2 = network['W1'], network['W2']
b1, b2 = network['b1'], network['b2']
u1 = np.dot(x, W1) + b1
z1 = functions.sigmoid(u1)
u2 = np.dot(z1, W2) + b2
y = u2
print_vec("総入力1", u1)
print_vec("中間層出力1", z1)
print_vec("総入力2", u2)
print_vec("出力1", y)
print("出力合計: " + str(np.sum(y)))
return z1, y
In [10]: # 誤差逆伝播
def backward(x, d, z1, y):
print("\n##### 誤差逆伝播開始 #####")
grad = {}
W1, W2 = network['W1'], network['W2']
b1, b2 = network['b1'], network['b2']
出力層でのデルタ
delta2 = functions.d_mean_squared_error(d, y)
b2の勾配
grad['b2'] = np.sum(delta2, axis=0)
W2の勾配
grad['W2'] = np.dot(z1.T, delta2)
中間層でのデルタ
delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1)
試してみよう
delta1 = np.dot(delta2, W2.T) * functions.d_sigmoid(z1)
delta1 = delta1[np.newaxis, :]
b1の勾配
grad['b1'] = np.sum(delta1, axis=0)
x = x[np.newaxis, :]
W1の勾配
grad['W1'] = np.dot(x.T, delta1)
print_vec("偏微分_重み1", grad["W1"])
print_vec("偏微分_重み2", grad["W2"])
print_vec("偏微分_バイアス1", grad["b1"])
print_vec("偏微分_バイアス2", grad["b2"])
1_3copy 2019/12/12 20'26
http://localhost:8890/nbconvert/html/Desktop/AI試験/DNN_code/lesson_1/1_3copy.ipynb?download=false 3 / 4 ページ
return grad
サンプルデータを作成
data_sets_size = 100000
data_sets = [0 for i in range(data_sets_size)]
for i in range(data_sets_size):
data_sets[i] = {}
ランダムな値を設定
data_sets[i]['x'] = np.random.rand(2) #コメントアウト
試してみよう_入力値の設定
data_sets[i]['x'] = np.random.rand(2) * 10 -5 # -5~5のランダム数値
目標出力を設定
data_sets[i]['d'] = f(data_sets[i]['x'])
losses = []
学習率
learning_rate = 0.07
抽出数
epoch = 1000
パラメータの初期化
network = init_network()
データのランダム抽出
random_datasets = np.random.choice(data_sets, epoch)
勾配降下の繰り返し
for dataset in random_datasets:
x, d = dataset['x'], dataset['d']
z1, y = forward(network, x)
grad = backward(x, d, z1, y)
パラメータに勾配適用
for key in ('W1', 'W2', 'b1', 'b2'):
network[key] -= learning_rate * grad[key]
誤差
loss = functions.mean_squared_error(d, y)
losses.append(loss)
print("##### 結果表示 #####")
lists = range(epoch)
plt.plot(lists, losses, '.')
グラフの表示
plt.show()
1_3copy 2019/12/12 20'26
http://localhost:8890/nbconvert/html/Desktop/AI試験/DNN_code/lesson_1/1_3copy.ipynb?download=false 4 / 4 ページ
In [ ]:
結果表示
活性化関数や数値を変えるとどれほど影響があるのか、図示しながら確認することで理解が深まった。