はじめに
この記事はQualiArts Advent Calendar 2020の22日目の記事になります。
本稿では数値の扱われ方の説明を行ない、浮動小数点数で表現できる整数値の有効桁数の話をします。
そして、最終的に単精度浮動小数であるfloat型では 123456789 が表現できないことを確認していきます。1
背景
ゲームの演出で獲得経験値をパラパラとアニメーションでカウントアップさせようとしていました。
とりあえず 0 から 123456789 までカウントアップさせる実装をしたものの、123456789 になってくれない。

くそぅ、、何度やっても 123456792 になってしまう!!!
結論から言うと、カウントアップの内部処理で値がfloat型として扱われており、float型では 123456789 の値は表現できなかったというオチでした。
int型の最大値は 2,147,483,647 で、float型の最大値は $3.402823466 × 10^{38}$ 。
何となくfloat型は大きな値も表現できると思っていたのですが、これは表現できる最大の数を表しているだけで、最大値までの全ての値を表現できると言っているわけではなかったのですね。
冷静に考えればその通り。お恥ずかしい話です。
せっかくの機会なので数値の表現周りを一から勉強をし直しました。
STK(その情報、ためになる人、きっといる)精神で本稿にまとめたいと思います。
値がズレた原因の説明のために、本稿では数値の扱われ方周りを細かく見ていきます。
固定小数点数
まずは固定小数点数という表現を見ていきます。
固定小数点数とは「小数点を固定して表現された数」です。
固定小数点数は**「〇〇.□□」のように書くことができます。
〇〇が整数部、□□が小数部、.**は小数点です。
そして△△進数で固定小数点数を書くときには、整数部と小数部はそれぞれ△△進数で表現されます。
と、文字を羅列して説明しても分かりづらいので図示すると次のようになります。

10進数の固定小数点数
それでは10進数の固定小数点数を見ていきます。
先ほどの図を10進数に変更すると次のようになります。
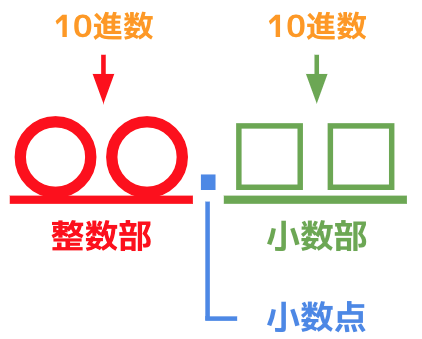
整数部と小数部がそれぞれ10進数で表現されていることが分かります。
これは僕らが日常でよく行なっている表現方法ですね。
10進数での固定小数点数の例
日本語的におかしいですが、21.75 を10進数の固定小数点数で表すと 21.75 となります。
2進数の固定小数点数
次は2進数の固定小数点数を見ていきます。
2進数の固定小数点数を図で表すと次のようになります。
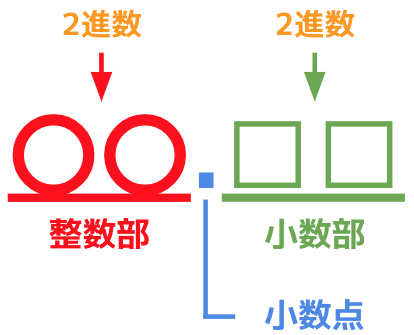
整数部と小数部がそれぞれ2進数で表現されていることが分かります。
2進数での固定小数点数の例
それでは、21.75 を2進数の固定小数点数で表します。
またこの時、全体を 32 ビット( 4 バイト)で表現するとします。
- 00010101.110000000000000000000000
- 000000010101.11000000000000000000
- 0000000000010101.1100000000000000
- 00000000000000010101.110000000000
すると、同じ 21.75 でも複数の表現方法があることが分かります(2進数の計算方法は後ほど説明します)。
2進数の固定小数点数のビット構成
今回は 16 ビット/ 16 ビットの分け方で見てみましょう。
- 0000000000010101.1100000000000000
この時の固定小数点数のビット構成は次の図のようになります。

ここに先ほどの数値が入ると次のようになります。

2進数の固定小数点数の整数部
それでは整数部を見ていきましょう。

2進数の整数部は一番右が10進数の $2^0$ を表し、左に行くにつれて $2^1$、$2^2$ ...という大きな数字を表します。
そのため今回の2進数を10進数に直すと、次の計算式により 21 になります。
$2^0+2^2+2^4=1+4+16=21$
また、この部分の説明では整数部は正の数しか扱わないと仮定しています。
負の数の説明は後ほど行います。
2進数の固定小数点数の小数部
次は小数部を見ていきましょう。

2進数の小数部は一番左が10進数の $2^{-1}$ を表し、右に行くにつれて $2^{-2}$、$2^{-3}$ ...という小さな数字を表します。
そのため、今回の2進数を10進数に直すと、次の計算式により 0.75 になります。
$2^{-1}+2^{-2}= \frac{1}{2}+\frac{1}{4}=0.5+0.25=0.75$
これにより、先ほどの整数部の計算と合わせて、
- 0000000000010101.1100000000000000
が 21.75 を表していたことが分かります。
ビット数の違いによる影響
さて、さきほど 21.75 は複数の表現方法があるという話をしました。
- 00010101.110000000000000000000000
- 000000010101.11000000000000000000
- 0000000000010101.1100000000000000
- 00000000000000010101.110000000000
次は小数点の位置が違うことで、どういう影響があるのかを見ていきましょう。
整数部のビットが多い時
整数部のビットが多い時を見ていく例として、28 ビット/ 4 ビットの分け方を見てみます。

この時、整数部の最上位ビットは $2^{27}$ のため、整数部では 0 〜 268,435,455( $2^{28}-1$ )までの数字を扱うことができます。
つまり、整数部のビットが多いと、より大きい数字を扱えることが分かります。
また、小数部の最下位ビットは $2^{-4}$ のため、小数部では 0.0625( $2^{-4}$ )までの精度しか扱うことができません。
つまり、小数部のビットが少ないと、細かな精度を扱えないことが分かります。
小数部のビットが多い時
小数部のビットが多い時を見ていく例として、4 ビット/ 28 ビットの分け方を見てみます。

この時、整数部の最上位ビットは $2^{3}$ のため、整数部では 0 〜 15( $2^{4}-1$ )までの数字しか扱うことができません。
つまり、整数部のビットが少ないと、小さな数字しか扱えないことが分かります。
また、小数部の最下位ビットは $2^{-28}$ のため、小数部では 0.0000000037252903( $2^{-28}$ )までの精度を扱うことができます。
つまり、小数部のビットが多いと、より細かな精度を扱えることが分かります。
ビット数の違いによる影響まとめ
ビット数の違いによる影響をまとめると次の表のようになります。
| ビット数の割り振り | 整数部 | 小数部 |
|---|---|---|
| 整数部が多くて小数部が少ない | より大きな数字を扱える | 細かな精度を扱えない |
| 整数部が少なくて小数部が多い | 小さな数字しか扱えない | より細かな精度を扱える |
実際に使われるビット数
では実際にはビット数はどのような割り振りで使われているのでしょうか。
実は、整数部と小数部が混在した固定小数点数では計算を行うのは難しいという課題があります。
そのため実際は「整数部のみ」or「小数部のみ」の固定小数点数が利用されることが多いです。
「整数部のみ」の固定小数点数は主に整数型を扱うために利用されます。

「小数部のみ」の固定小数点数は主に後ほど説明する浮動小数点数内で利用されます。

そして、整数と小数が混在した値は、後ほど説明する浮動小数点数で扱います。
符号付き整数
ここまでは、整数を扱う際は全てのビットを整数の絶対値情報として扱い、符号なし整数(正の整数)だけを扱ってきました。

たとえばこの時は、0 〜 65,535( $2^{16}-1$ )の値を扱うことができました。
ここで最上位のビットを符号として扱うことで、符号付き整数を扱えるようになります。

この時、符号ビットが 0 の時は正の整数、1 の時は負の整数を表します。
そしてこの符号付き整数は大きく3つの表現方法が存在します。
| +11 | -11 | 正と負の変換方法 | |
|---|---|---|---|
| 符号+絶対値 | 0 0001011 | 1 0001011 | 符号ビットを反転 |
| 1の補数 | 0 0001011 | 1 1110100 | 符号ビットを反転し、絶対値ビットも全て反転 |
| 2の補数 | 0 0001011 | 1 1110101 | 符号ビットを反転し、絶対値ビットも全て反転し、1 を足す |
| ※説明を簡単化するため、8 ビット整数で説明をしています。 |
ここからは正負の加算処理を見ながらこの 3 つの表現方法を比較していきます。
符号+絶対値
| +11 | -11 | 正と負の変換方法 | |
|---|---|---|---|
| 符号+絶対値 | 0 0001011 | 1 0001011 | 符号ビットを反転 |
符号+絶対値の加算処理を考えます。
たとえば +8 と -11 の 2 数を加える際には下記の手順が必要になります。
- 各々の符号を調べる(符号が同じならば 2 つの数の絶対値を足して終了)
- 符号が異なる場合は 2 数の数の絶対値の大きさを比べる
- 絶対値が大きい方の絶対値から小さい方の絶対値を引く
- 絶対値が大きい方の符号を結果の符号として採用する
式で表すと次のようになります。
( +8 ) + ( -11 ) = -( 11 - 8 ) = -3
( 0 0001000 ) + ( 1 0001011 ) = 1 ( 0001011 - 001000 ) = 1 0000011
このように符号+絶対値の加算では、数の比較、加算、減算、場合分けなど様々な処理が必要となるため実現するには少し手間が掛かります。
1 の補数
| +11 | -11 | 正と負の変換方法 | |
|---|---|---|---|
| 1 の補数 | 0 0001011 | 1 1110100 | 符号ビットを反転し、絶対値ビットも全て反転 |
1 の補数の加算では、符号を含め 2 数を加算し、符号ビットから桁上がりがあれば上がった桁を捨てて、結果に 1 を加えます。
それでは、$(+4)+(+11)$ の計算を見てみます。

4( 0 0000100 )と 11( 0 0001011 )の加算の結果が確かに 15( 0 0001111 )になっていることを確認できます。
次に、$(-4)+(+11)$ の計算を見てみます。

符号ビットから桁上がりが発生していることが分かります。
なので、上がった桁を捨てて、結果に 1 を加えます。

これにより、-4( 1 1111011 )と 11( 0 0001011 )の加算の結果が確かに 7( 0 0000111 )になっていることを確認できます。
また 1 の補数では、+0( 0 0000000 )と -0( 1 1111111 )の 2 つの 0 が存在します。
例えば +11( 0 0001011 )と -11( 1 1110100 )を加算すると -0( 1 1111111 )になることを確認できます。

そして、8 ビットの時の値は、-127 〜 127 の値を扱うことができます。
2 の補数
| +11 | -11 | 正と負の変換方法 | |
|---|---|---|---|
| 2 の補数 | 0 0001011 | 1 1110101 | 符号ビットを反転し、絶対値ビットも全て反転し、1 を足す |
2 の補数の加算では、符号を含め 2 数を加算し、符号ビットから桁上がりがあれば上がった桁を捨てます。
それでは 1 の補数の時と同様の加算を見ていきます。
$(+4)+(+11)$ の計算に関しては 1 の補数の時と同様なので省略します。
それでは、$(-4)+(+11)$ の計算を見てみます。
-4 の 2 の補数表現は 4( 0 0000100 )の符号ビットと絶対値ビットを反転させて 1 を足した 1 1111100 です。

この時、符号ビットから桁上がりが発生しているので上がった桁を捨てています。
これにより、-4( 1 1111100 )と 11( 0 0001011 )の加算の結果が確かに 7( 0 0000111 )になっていることを確認できます。
また 2 の補数では、-0 が存在せず、+0( 0 0000000 )のみが存在します。
例えば1の補数の説明の際に行なった +11( 0 0001011 )と -11( 1 1110101 )の加算結果も +0( 0 0000000 )になることを確認できます。

そして、-0 が無くなったので負の数を 1 つ多く扱えるようになるため、8 ビットの時の値は、-128 〜 127 の値を扱うことができます。
符号付き整数表現の比較
以上を踏まえて符号付き整数表現をまとめると次の表のようになります。
| +0 | -0 | 最大値 | 最小値 | |
|---|---|---|---|---|
| 符号+絶対値 | 0 0000000 | 1 0000000 | 127 0 1111111 |
-127 1 1111111 |
| 1 の補数 | 0 0000000 | 1 1111111 | 127 0 1111111 |
-127 1 0000000 |
| 2 の補数 | 0 0000000 | なし | 127 0 1111111 |
-128 1 0000000 |
この 3 つの中では、0 が 1 種類しか存在せず、表現できる範囲も広く、計算も単純な 2 の補数が最も優れていると考えられます。
そのため、現実では符号付き整数は 2 の補数で表現されることが多いです。
整数型との対応
以上で固定小数点数に関する説明が終わりです。
最後に整数型と固定小数点数の表現方法の対応を表にまとめると次のようになります。
※ 環境によっては異なることもあります。
| 型 | 説明 | 範囲 | 固定小数点数での表現方法 |
|---|---|---|---|
| sbyte | 符号付き 8 ビット整数 | -128 〜 127 | 2 の補数の符号付き整数( 8 ビット) |
| byte | 符号なし 8 ビット整数 | 0 〜 255 | 符号なし整数( 8 ビット) |
| short | 符号付き 16 ビット整数 | -32,768 〜 32,767 | 2の 補数の符号付き整数( 16 ビット) |
| ushort | 符号なし 16 ビット整数 | 0 〜 65,535 | 符号なし整数( 16 ビット) |
| int | 符号付き 32 ビット整数 | -2,147,483,648 〜 2,147,483,647 | 2 の補数の符号付き整数( 32 ビット) |
| uint | 符号なし 32 ビット整数 | 0 〜 4,294,967,295 | 符号なし整数( 32 ビット) |
| long | 符号付き 64 ビット整数 | -9,223,372,036,854,775,808 〜 9,223,372,036,854,775,807 |
2 の補数の符号付き整数( 64 ビット) |
| ulong | 符号なし 64 ビット整数 | 0 〜 18,446,744,073,709,551,615 | 符号なし整数( 64 ビット) |
浮動小数点数
次は浮動小数点数という表現を見ていきます。
浮動小数点数とは「小数点を浮動して(一定の場所に定めずに)表現された数」です。
固定小数点数の時と同様の説明を行うと、浮動小数点数は**「±〇〇×△△の□□乗」**のように書くことができます。
±が符号、〇〇が仮数(かすう)、△△が基数(きすう)、□□が指数(しすう)です。
そして△△進数で浮動小数点数を書くときには、仮数と指数はそれぞれ△△進数で表現され、基数の値は進数の値の△△と一致します。
今回も、文字を羅列して説明しても分かりづらいので図示すると次のようになります。
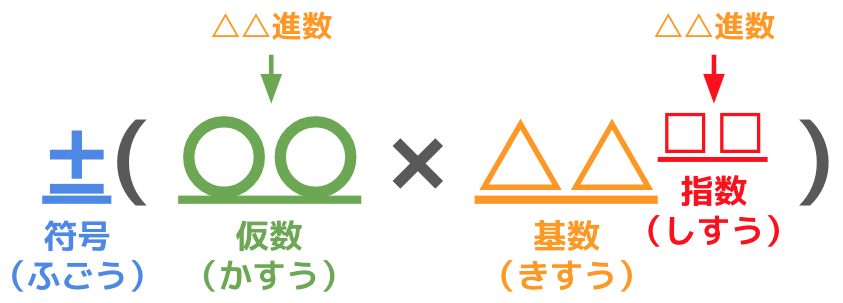
10 進数の浮動小数点数
それでは10進数の浮動小数点数を見ていきます。
先ほどの図を10進数に変更すると次のようになります。

仮数と指数がそれぞれ10進数で表現され、基数の値が 10 になっていることを確認できます。
10進数での浮動小数点数の例
それでは、21.75 を10進数の浮動小数点数で表します。

すると、上記のように同じ 21.75 でも複数の表現方法があることが分かります。
これを一意に決めることができないかを考えます。
浮動小数点数の正規化表現
基数の値をR、仮数の値をmとした時に、0 以外の値は 1 ≦ m < **R** となるように表現( 正規化表現 )できます。
つまり、先ほどの 21.75 を浮動小数点数の正規化表現で表すと、
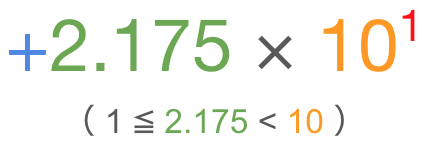
のようになり、浮動小数点数を一意に表すことができるようになります。
2進数の浮動小数点数
次は2進数の浮動小数点数を見ていきます。
2進数の浮動小数点数を図で表すと次のようになります。
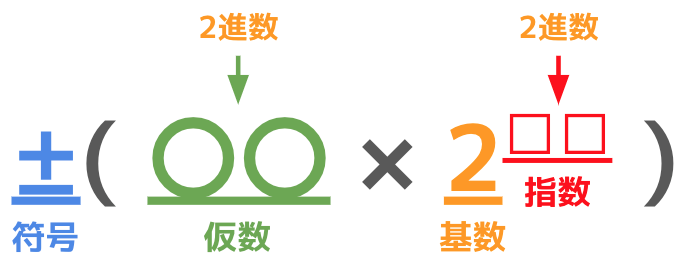
仮数と指数がそれぞれ2進数で表現され、基数の値が 2 になっていることを確認できます。
2進数での浮動小数点数の例
それでは、 21.75 を2進数の浮動小数点数で表します。

すると、10進数の浮動小数点数の時と同様に、同じ 21.75 でも複数の表現方法があることが分かります。
浮動小数点数の正規化表現
21.75 も先ほどと同様に正規化表現を用いて一意に表すことができます。

2進数の浮動小数点数ではこの値を元にビット構成を構築します。
2進数の浮動小数点数のビット構成(単精度浮動小数点数)
今回は 32 ビットの浮動小数点数(単精度浮動小数点数)のビット構成を見ていきます。
この時の浮動小数点数のビット構成は次の図のようになります。
※ 今回は浮動小数点算術に関する標準であるIEEE754におけるビット構成で説明を行います。
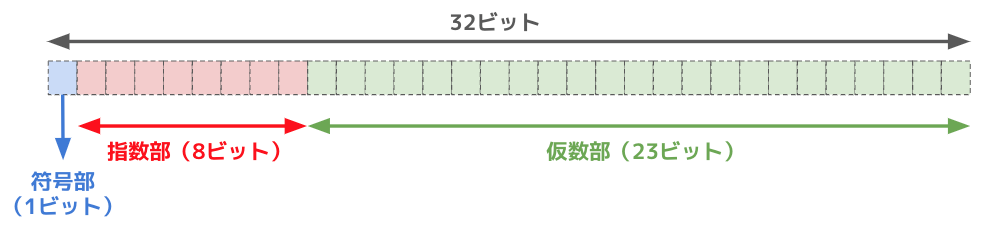
ここのビット構成に先ほど正規化した値を当てはめていきます。

浮動小数点数の符号部
浮動小数点数では符号ビットが 0 の時は正の実数、1 の時は負の実数を表します。
また、浮動小数点数では負の時に他のビットを反転させたりはしません。
固定小数点数の符号+絶対値がイメージに近いかもしれません。
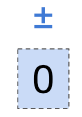
今回は正の値なので符号ビットには 0 が入ります。
浮動小数点数の指数部
浮動小数点数では指数は負の値も表現できるようにします。
この時、指数部は符号付き整数になるのですが、指数部には実際の指数に +127 をした値を代入することで符号付き整数を表現します。
これは符号+絶対値、1 の補数、2 の補数のどれとも違う表現になります。
指数部の値と実際の指数( 2 のべき乗数)の関係をまとめると次の表のようになります。

また、指数部が 0 や 255 の時は、0 や無限大などを表したりと特殊な使われ方をします。
今回は $2^4$( $2^{0000100}$ )を表したいため、4 に 127 を加算した 131( 00000100 に 01111111 を加算した 10000011 )を指数部に入れます。
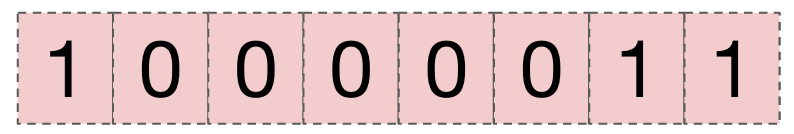
浮動小数点数の仮数部
正規化をしたことにより、2進数の仮数部の最上位ビットは必ず 1 になります。

そのため、より多くの数値を表現するために、仮数部には最上位ビットを省略して値を格納します。

ちなみにここで先ほど説明した小数のみの固定小数点数が用いられています。
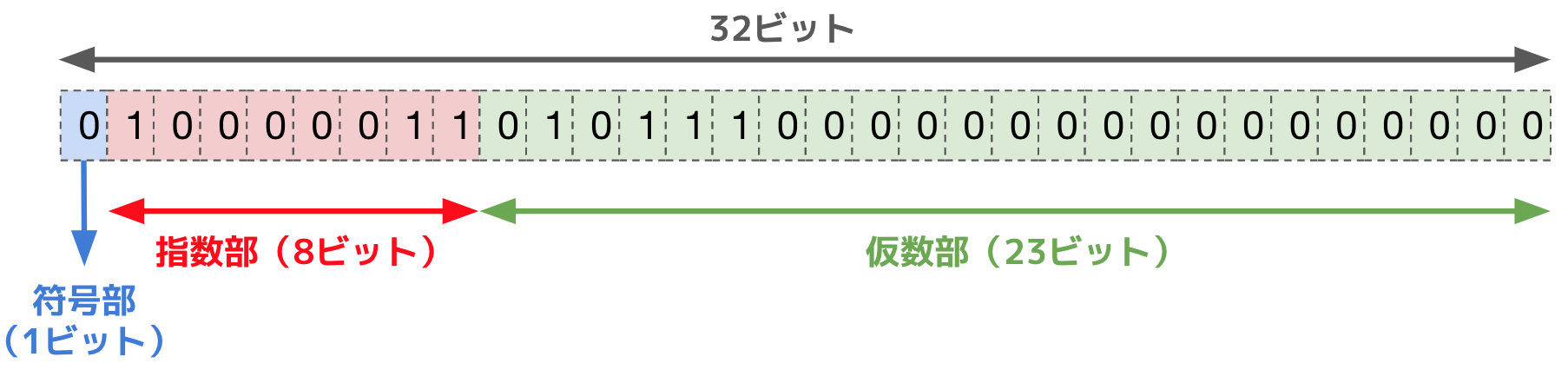
21.75 の浮動小数点数のビット構成
以上を合わせることで、21.75 の浮動小数点数のビット構成は次のようになります。
実数型との対応
ここまでは単精度浮動小数を見ていきましたが、浮動小数は大きく半精度浮動小数、単精度浮動小数、倍精度浮動小数などがあります。
それぞれのビット構成は次のようになります。

以上で浮動小数点数に関する説明は終わりです。
最後に実数型と浮動小数点数の表現方法の対応を表にまとめると次のようになります。
※ 環境によっては異なることもあります。
| 型 | 種類 | 範囲 |
|---|---|---|
| half | 半精度浮動小数( 16 ビット) | 最小の正の数 $6.103515 × 10^{-5}$ 最大の正の数 $6.5504 × 10^{4}$ |
| float | 単精度浮動小数( 32 ビット) | 最小の正の数 $1.175494351 × 10^{-38}$ 最大の正の数 $3.402823466 × 10^{38}$ |
| double | 倍精度浮動小数( 64 ビット) | 最小の正の数 $2.2250738585072014 × 10^{-308}$ 最大の正の数 $1.7976931348623158 × 10^{308}$ |
float型で 123456789 が表現できなかった原因
先ほどのfloat型の表現範囲を改めて確認します。
| 型 | 種類 | 範囲 |
|---|---|---|
| float | 単精度浮動小数(32ビット) | 最小の正の数 $1.175494351 × 10^{-38}$ 最大の正の数 $3.402823466 × 10^{38}$ |
この表を見ると、123456789 は最大の正の数に収まっている気がします。
しかし、この最大の正の数は表現できる最大の値を表しているだけであり、最大値までの全ての値を表現できるとは言っているわけではありません。
それではfloat型の整数の有効桁数を見ていきます。
float型の整数の有効桁数
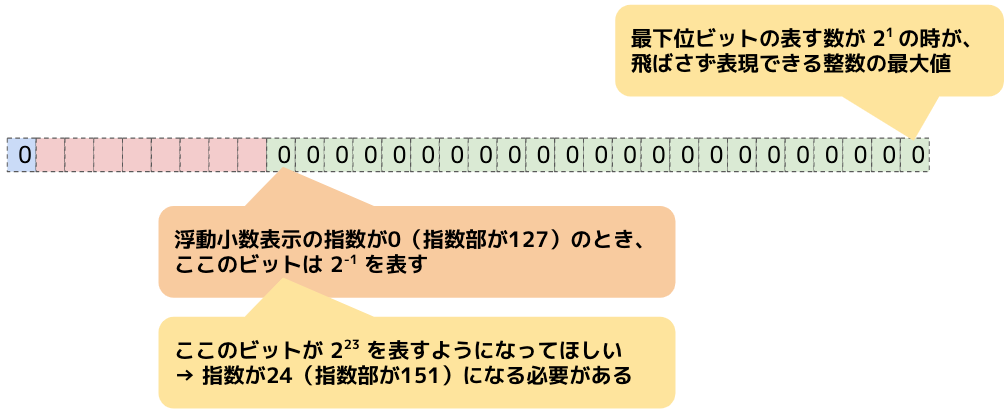
単精度浮動小数の符号部ビットが 0 、仮数部ビットが全て 0 で、仮数部の最下位ビットが $2^1$ を表す時が、float型で値を飛ばさずに表現できる整数の最大値です。

ちょっとイメージが付きづらいなと言う方は、単精度浮動小数の符号部ビットが 0 、仮数部ビットが全て 1 で、仮数部の最下位ビットが $2^0$ を表す時が、float型で値を飛ばさずに表現できる整数の最大値の 1 つ前と言った方がイメージが付きやすいかもしれないです。

また、浮動小数表示の指数が 0(指数部が 127 )のとき、仮数部の最上位ビットは $2^{-1}$ を表します。

今回は、仮数部の最下位ビットが $2^1$ を表してほしいため、仮数部の最上位ビットは $2^{23}$ を表す必要があります。
そのため、指数が 24(指数部が 151 )になる必要があります。
それを元に指数部に値を代入すると次のようになります。
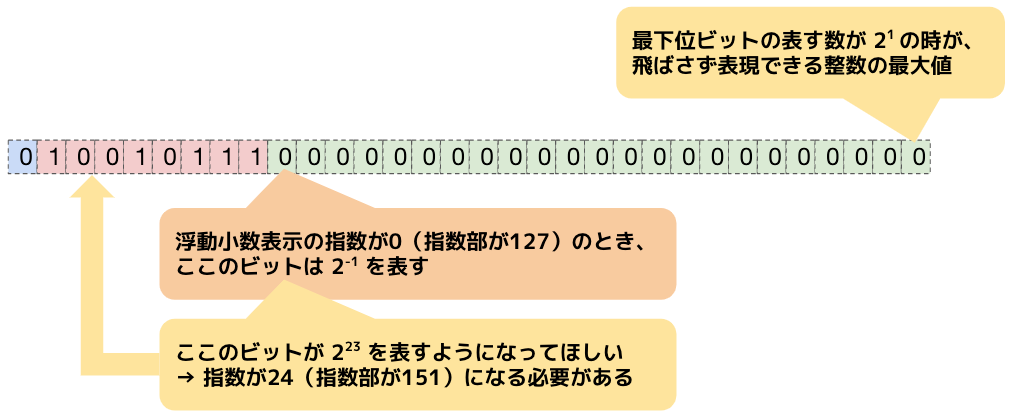
この時の値は、16777216( $2^{24}$ )です。
これ以降は、表現できる値が飛び飛びになってしまいます。
16777215 → 16777216 → (16777217) → 16777218 → (16777219) → 16777220
※ ( ) の値は最下位ビットの表す数が $2^1(=2)$ のため表現できない。
よって、float型で値を飛ばさずに表現が行える整数xの範囲は、
-16777216 ≦ x ≦ 16777216
そして、123456789 は 16777216 よりも大きく、float型によって表現できない値だったため正しく表示が行われませんでした。
以上より、float型で正確に表現できる整数は 7 桁までということがわかりました。
double型の整数の有効桁数
ちなみに、double型で値を飛ばさずに表現が行える整数xの範囲は、$2^{53} ≒ 9.0071993 × 10^{15}$ なので、
$-9.0071993 × 10^{15} ≦ x ≦ 9.0071993 × 10^{15}$
つまり、double型で正確に表現できる整数は 15 桁までということがわかりました。
まとめ
本稿では数値の扱われ方の説明を行ない、浮動小数点数で表現できる整数値の有効桁数の話をしました。
その結果、float型の有効桁数は 7 桁、double型の有効桁数は 15 桁ということがわかりました。
そして、float型で 123456789 が表現できないことも確認しました。
カウントアップで 123456789 が表示されなかった問題は気付けば単純な有効桁数の問題でした。
今回はたまたま 123456789 という数字を入れたから気付いたものの、普段から有効桁数は気をつけないとなと思いました。
特に内部でfloat型に変換されていないかなどは意識して見ないといけないです。
あとは実装時は有効桁数に収まっているから問題なかったのに、運用で桁数が増えた結果、いつのまにか有効桁数に収まらなくなっているとかも気をつけないといけないですね。恐ろしい話です。
本稿がどなたかの役に立ちましたら幸いです。
-
浮動小数点算術に関する標準であるIEEE754のfloat型における話にはなります。 ↩