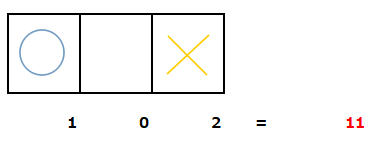はじめに
どうも、y-tetsuです。
今回、機械学習の練習として重回帰分析を用いた三目並べのAIを作ってみたのでメモします。もともとはリバーシ(オセロ)のAIを重回帰分析で作りたいと思っていたのですが、個人的にハードルが高く、まずはより簡単そうな三目並べで試してみることにしました。
本記事の大まかな流れは以下のとおりです。
- 三目並べのゲーム部分を実装する
- ランダム対戦の棋譜より盤面に得点を付ける
- 盤面から得点を予測する回帰式を決める
- 回帰式に合わせたデータセットを作成する
- データセットを重回帰分析し回帰式を求める
- 回帰式を使って得点予測するAIを実装する
- 作ったAIと対戦するプログラムを実装する
あくまで機械学習の初心者が、試行錯誤して得た結果のメモです。十分に検証された確かなものではございませんので、あらかじめご了承願います。
Pythonで便利に使える機械学習ライブラリの1つscikit-learn(サイキットラーン)を用いて、なんちゃってな回帰式でサクッとAIを作り、実際に対戦してみるまでのお話となっています。
できたもの
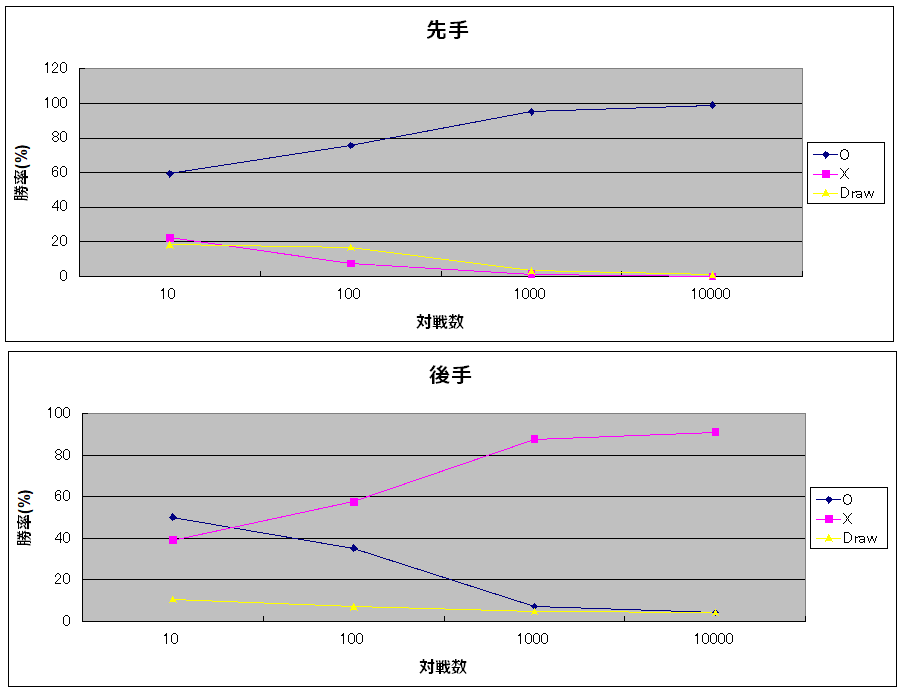
まず先に、今回作った三目並べAIの強さを示す結果を示します。「重回帰分析AI vs ランダムな打ち手のAI」にて、先手/後手を入れ替えて10万回ずつ対戦させたものです。なおAIの学習には、1万回のランダム対戦により作成した棋譜を用いました。
| 重回帰分析AIの手番 | 勝ち | 負け | 引き分け |
|---|---|---|---|
| 先手 | 99.0% (98989/100000) | 0.0% (0/100000) | 1.0% (1011/100000) |
| 後手 | 91.0% (90981/100000) | 4.7% (4712/100000) | 4.3% (4307/100000) |
先手番では負け率が0%と、おそらく負けないだろう強さになっていました。(後手番での負けは非常に残念ですが…)
このように適当にプレイした対戦結果を重回帰分析することでも、それなりのAIが作成できそうだ!!という所をお伝えできればいいなと思います。
動作確認環境
本記事のプログラムを実際に動かされる際は、あらかじめ以下のご準備をお願いします。
Python3.9以上のインストール
本記事のプログラムは全てPythonで書かれております。バージョン3.9以上であれば問題なく動作すると思います。
pandasのインストール
データ解析を支援する機能を提供するライブラリです。今回はcsvファイルの読み込みに使っています。
> pip install pandas
scikit-learnのインストール
Python用の機械学習ライブラリです。今回は重回帰分析に使用しています。
> pip install scikit-learn
三目並べのゲーム部分を実装する
まず、三目並べを動かすための土台としてゲームの基礎部分を実装します。次に、重回帰分析する上で必要となる棋譜のデータを作成するために対戦シミュレータを実装します。
三目並べとは
三目並べとは、○×(マルバツ、マルペケ)ゲームと呼ばれたりもします。3×3の格子の中に先手と後手が"〇"と"×"を交互に書き込み、先に3つ揃えて勝ちを競うゲームです。
三目並べのプログラム
早速ですが三目並べのプログラム全体を示します。実行するとランダムに打つ対戦相手と遊べるものになっています。中身の説明は追って行います。
from random import randint
B = 0
O = 1
X = 2
D = 3
KEY = ' OX'
class TicTacToe:
def __init__(self, player1, player2):
self.move = {O: player1, X: player2}
def show(self, board):
print()
for i in range(3):
print(' ' + '|'.join([KEY[board[i * 3 + j]] for j in range(3)]))
if i < 2:
print(' -+-+-')
print()
def judge(self, board):
patterns = [(0, 1, 2), (3, 4, 5), (6, 7, 8), # horizontal
(0, 3, 6), (1, 4, 7), (2, 5, 8), # vertical
(0, 4, 8), (2, 4, 6)] # diagonal
for c1, c2, c3 in patterns:
if board[c1] and board[c1] == board[c2] == board[c3]:
return board[c1]
if B not in board:
return D
return B
def play(self):
try:
while True:
turn, board = O, [B for _ in range(9)]
while True:
self.show(board)
if winner := self.judge(board):
if winner == D:
print('--- Draw ---')
else:
print(f'*** {KEY[winner]} win!! ***')
input('\n>>> Press enter to start new game')
break
print(f'turn : {KEY[turn]}')
move = self.move[turn](board, turn)
board[move] = turn
turn = X if turn == O else O
except KeyboardInterrupt:
pass
def simulate(self, num=100):
count, ret, records = 0, [0 for _ in range(4)], []
while True:
turn, board, record = O, [B for _ in range(9)], []
while True:
if winner := self.judge(board):
ret[winner] += 1
count += 1
records += [[winner] + record]
break
move = self.move[turn](board, turn)
board[move] = turn
record += [move]
turn = X if turn == O else O
if count >= num:
print(f'O = {ret[O]}/{num} ({ret[O]/num*100:.1f}%)')
print(f'X = {ret[X]}/{num} ({ret[X]/num*100:.1f}%)')
print(f'D = {ret[D]}/{num} ({ret[D]/num*100:.1f}%)')
break
return records
def user(board, turn):
while True:
try:
move = int(input('> '))
if move < len(board) and not board[move]:
return move
except ValueError:
pass
def rand(board, turn):
blank = [i for i, cell in enumerate(board) if cell == B]
rand_index = randint(0, len(blank) - 1)
return blank[rand_index]
if __name__ == '__main__':
tictactoe = TicTacToe(user, rand)
tictactoe.play()
(実行方法)
> python tictactoe.py
(遊び方)
あなたの手番の時に、打ちたいマス目を番号で指定してください。
| |
-+-+-
| |
-+-+-
| |
turn : O
>
(マス目の番号)
0|1|2
-+-+-
3|4|5
-+-+-
6|7|8
(右上の角に打つ場合)
| |
-+-+-
| |
-+-+-
| |
turn : O
> 2
| |O
-+-+-
| |
-+-+-
| |
中断する際は、Ctrl+Cを押してください。
プログラムの中身を少しずつ見ていきます。
マス目の状態
マス目の状態は、"空き"、"先手"、"後手"の3種類があります。以下で定義しています。
B = 0
O = 1
X = 2
| マスの状態 | 意味 |
|---|---|
| B | 空き |
| O | 先手 |
| X | 後手 |
勝敗判定
勝敗判定の結果として、"対戦中"、"先手の勝ち"、"後手の勝ち"、"引き分け"の4種類があります。(一部、先ほどのマス目の状態と併用しています)
B = 0
O = 1
X = 2
D = 3
| 判定結果 | 意味 |
|---|---|
| B | 対戦中 |
| O | 先手の勝ち |
| X | 後手の勝ち |
| D | 引き分け |
盤面の表示
盤面は9つの要素を持つ一次元のリストとしています。盤面表示はshowメソッドで実施しています。引数のboardが盤面のリストを表しており、3×3の格子状に盤面の状態を標準出力します。
KEY = ' OX'
class TicTacToe:
def show(self, board):
print()
for i in range(3):
print(' ' + '|'.join([KEY[board[i * 3 + j]] for j in range(3)]))
if i < 2:
print(' -+-+-')
print()
(出力例)
boardが
board = [B, B, O, B, X, B, B, B, B]
のとき、
| |O
-+-+-
|X|
-+-+-
| |
と表示されます。
勝敗の判定
judgeにより、現在の盤面の勝敗判定を行います。
class TicTacToe:
def judge(self, board):
patterns = [(0, 1, 2), (3, 4, 5), (6, 7, 8), # horizontal
(0, 3, 6), (1, 4, 7), (2, 5, 8), # vertical
(0, 4, 8), (2, 4, 6)] # diagonal
for c1, c2, c3 in patterns:
if board[c1] and board[c1] == board[c2] == board[c3]:
return board[c1]
if B not in board:
return D
return B
patternsにはあらかじめ、縦横斜めの8列のマス目の位置を用意しています。いずれかの列が"先手"か"後手"で揃っていないかを調べ、揃っている場合その手番を返します。また、揃っていない場合、かつ空きがない場合は"引き分け"を返します。引き分けでもない場合は"対戦中"を返します。
| 条件 | 判定結果 | 戻り値 |
|---|---|---|
| 先手が揃っている | 先手の勝ち | O |
| 後手が揃っている | 後手の勝ち | X |
| 先手も後手も揃っていない、かつ空きマスなし | 引き分け | D |
| 先手も後手も揃っていない、かつ空きマスあり | 対戦中 | B |
ゲーム進行
playによりゲームの進行を行います。手を打つAIを自由に切り替えられるよう、インスタンス初期化メソッドの引数にてplayer1(先手)、player2(後手)を取得するようにしています。それぞれの引数には、手を選ぶAI(関数)を指定します。
class TicTacToe:
def __init__(self, player1, player2):
self.move = {O: player1, X: player2}
def play(self):
try:
while True:
turn, board = O, [B for _ in range(9)]
while True:
self.show(board)
if winner := self.judge(board):
if winner == D:
print('--- Draw ---')
else:
print(f'*** {KEY[winner]} win!! ***')
input('\n>>> Press enter to start new game')
break
print(f'turn : {KEY[turn]}')
move = self.move[turn](board, turn)
board[move] = turn
turn = X if turn == O else O
except KeyboardInterrupt:
pass
1回の対戦は、以下の1.~6.のループで構成されています。
- 盤面の表示
- 勝敗判定し決着していれば終了
- 手番の表示
- 打ち手の取得
- 盤面に手を置く
- 手番の更新
対戦が終了すると、次のメッセージが表示されます。この時、Enterを押すと再び新規にゲームが始まります。
>>> Press enter to start new game
Ctrl+Cで中断できるようにするために、KeyboardInterruptの例外受付時は、ループを抜けてそのまま終了するようにしています。
move = self.move[turn](board, turn)
手を選ぶAI(関数)は、上記のようにコールされます。引数としてboard(盤面)とturn(手番)を持ち、処理の結果として打ち手を返す事が前提となっています。
続いて、手を選ぶAIの作成例を示します。
ユーザー入力
ユーザー(人)が番号入力により手を打てるようにするための関数です。プログラムとしては人の操作もAIの関数と同様に扱っています。本関数をplayer1やplayer2に指定すると、人が遊べるようになっています。
def user(board, turn):
while True:
try:
move = int(input('> '))
if move < len(board) and not board[move]:
return move
except ValueError:
pass
入力された数値が盤面の範囲かつ、空きマスの場合は手を受け付けて、そうでない場合は再入力を求めます。turnは、後で作るAIが自分の手番に応じて処理を切り替えるために用意したもので、本関数では未使用です。
プログラム実行部分を以下にすると、対人戦が行えます。
if __name__ == '__main__':
tictactoe = TicTacToe(user, user)
tictactoe.play()
ランダムに打つAI
適当に打つAIです。重回帰分析で使う棋譜を作成するために働いてもらいます。対戦するともちろん弱いです。こちらもturnは未使用です。
from random import randint
def rand(board, turn):
blank = [i for i, cell in enumerate(board) if cell == B]
rand_index = randint(0, len(blank) - 1)
return blank[rand_index]
空きマスを探し、その中からランダムに1つ選んだ手を打ちます。
randint(開始, 終了)は、開始と終了を含む範囲のランダムな整数を返す関数です。
対戦シミュレータ
コンピュータ同士を対戦させ、棋譜を自動で作成するためのシミュレータです。numで指定した回数だけ対戦を繰り返します。対戦が終了すると対戦結果を表示し、棋譜のデータ(records)を返します。
class TicTacToe:
def simulate(self, num=100):
count, ret, records = 0, [0 for _ in range(4)], []
while True:
turn, board, record = O, [B for _ in range(9)], []
while True:
if winner := self.judge(board):
ret[winner] += 1
count += 1
records += [[winner] + record]
break
move = self.move[turn](board, turn)
board[move] = turn
record += [move]
turn = X if turn == O else O
if count >= num:
print(f'O = {ret[O]}/{num} ({ret[O]/num*100:.1f}%)')
print(f'X = {ret[X]}/{num} ({ret[X]/num*100:.1f}%)')
print(f'D = {ret[D]}/{num} ({ret[D]/num*100:.1f}%)')
break
return records
プログラム実行部分を以下にすると、10回分の対戦結果が得られます。
if __name__ == '__main__':
tictactoe = TicTacToe(rand, rand)
for record in tictactoe.simulate(10):
print(record)
実行結果は以下。(ランダムな対戦結果のため、表示は異なる場合があります)
O = 7/10 (70.0%)
X = 2/10 (20.0%)
D = 1/10 (10.0%)
[1, 5, 1, 7, 2, 3, 8, 0, 4, 6]
[2, 2, 5, 1, 0, 8, 3, 6, 4]
[1, 7, 3, 6, 4, 8]
[3, 2, 8, 6, 1, 7, 3, 0, 4, 5]
[1, 8, 1, 0, 5, 3, 2, 4]
[1, 7, 8, 4, 0, 3, 6, 1]
[1, 4, 0, 2, 1, 6]
[1, 1, 4, 5, 8, 0, 7, 3, 2, 6]
[2, 1, 8, 6, 5, 7, 2]
[1, 5, 6, 2, 1, 4, 3, 8]
先手の勝ち、後手の勝ち、引き分けの割合を表示したのち、10回の対戦の棋譜を表示しています。
棋譜といっても、単にプレイヤーが置いたマスの番号をリストに格納しただけのものです。ただし、リストの先頭の値は"勝敗"を表しています。なお、手番は暗黙的に毎回交代するものとして扱います。
| 勝敗 | 意味 |
|---|---|
| 1 | 先手の勝ち |
| 2 | 後手の勝ち |
| 3 | 引き分け |
(例)
[1, 5, 1, 7, 2, 3, 8, 0, 4, 6]
先頭の"1"により、先手の"勝ち"を意味し、以下の順で手を打ったことを示しています。
| 手数 | 手番 | 打ち手 |
|---|---|---|
| 1 | 先手 | 5 |
| 2 | 後手 | 1 |
| 3 | 先手 | 7 |
| 4 | 後手 | 2 |
| 5 | 先手 | 3 |
| 6 | 後手 | 8 |
| 7 | 先手 | 0 |
| 8 | 後手 | 4 |
| 9 | 先手 | 6 |
(最終盤面)
O|X|X
-+-+-
O|X|O
-+-+-
O|O|X
以上で、三目並べのゲーム部分の実装は終わりになります。
続いては、この三目並べの対戦シミュレータで実際に棋譜を作成し、それらを元に盤面の得点付けを行うことで、重回帰分析の準備を進めていきます。
ランダム対戦の棋譜より盤面に得点を付ける
ここではまず、前章で作成した対戦シミュレータを使って、コンピュータ同士を対戦させた棋譜を集めます。そして、その結果得られた棋譜の勝敗を元に、各盤面の得点付けを行います。最終的に、ここで付けた得点の傾向を回帰式で予測することになります。
たくさんの棋譜が欲しいので、今回は簡単のため、対戦させるコンピュータはランダムに打ち手を選ぶもの同士とします。おそらく強いプレイヤー同士が対戦した棋譜が得られれば、より効率よく強いAIにできそうです。
盤面の得点を決めるプログラム
以下は今回実装した、盤面の得点を決めるためのプログラムです。コンピュータ同士で対戦した複数の棋譜を元に、勝敗に応じて加点/減点し、盤面毎の得点を集計しています。
from tictactoe import TicTacToe, B, O, X, rand
O_WIN = 10
X_WIN = -10
DRAW = 0
class RandomRecords:
def __init__(self):
self.t = TicTacToe(rand, rand)
def scoring(self, num):
scores = {}
records = self.t.simulate(num)
for record in records:
winner = record.pop(0)
score = O_WIN if winner == O else X_WIN if winner == X else DRAW
turn, board = O, [B] * 9
for move in record:
board[move] = turn
key = tuple(board)
if key not in scores:
scores[key] = {'total': 0, 'count': 0}
scores[key]['total'] += score
scores[key]['count'] += 1
turn = X if turn == O else O
return scores
if __name__ == '__main__':
records = RandomRecords()
for key, value in records.scoring(1).items():
print(key, value)
続いてプログラムの中身を説明します。
ランダムな打ち手の対戦を準備する
初期化時に、ランダムな打ち手のプレイヤー同士で、三目並べを行うよう準備します。
class RandomRecords:
def __init__(self):
self.t = TicTacToe(rand, rand)
盤面に得点を付ける
numで指定した回数だけ対戦を行い、それによって得られた棋譜を元に、盤面に得点を付けます。
class RandomRecords:
def scoring(self, num):
scores = {}
records = self.t.simulate(num)
for record in records:
winner = record.pop(0)
score = O_WIN if winner == O else X_WIN if winner == X else DRAW
turn, board = O, [B] * 9
for move in record:
board[move] = turn
key = tuple(board)
if key not in scores:
scores[key] = {'total': 0, 'count': 0}
scores[key]['total'] += score
scores[key]['count'] += 1
turn = X if turn == O else O
return scores
先手(O_WIN)が勝った場合は10点、後手(X_WIN)の場合は-10点、引き分け(DRAW)の場合は0としました。点数の付け方は、勝ち負け引き分けが均等に評価できそうかな、という思い付きの値を設定しています。ここをもっと掘り下げても、より精度の高い分析が行えると思います。
O_WIN = 10
X_WIN = -10
DRAW = 0
得点付けの手順は以下の通りです。
- 棋譜の勝敗を取得する
- 1に応じた得点(10 or -10 or 0)を取得する
- 1.の初手からのすべての盤面(
key)に対する得点データについて、合計値(total)に2.の値を加算し、回数(count)を1増やす
例として、1回対戦させた結果を見てみます。
if __name__ == '__main__':
records = RandomRecords()
for key, value in records.scoring(1).items():
print(key, value)
(実行方法)
python scoring.py
(実行結果)
O = 1/1 (100.0%)
X = 0/1 (0.0%)
D = 0/1 (0.0%)
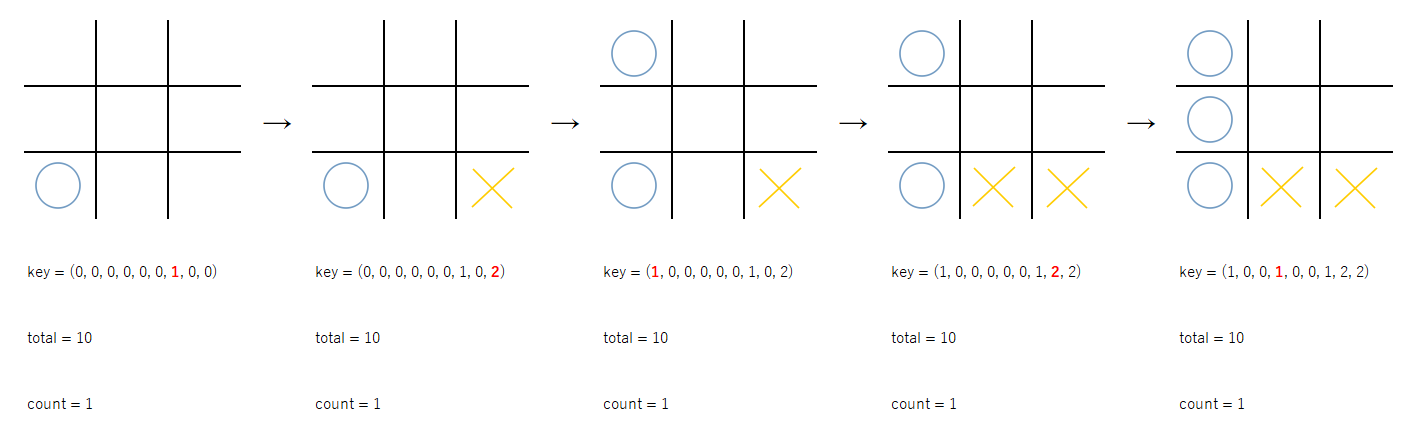
(0, 0, 0, 0, 0, 0, 1, 0, 0) {'total': 10, 'count': 1}
(0, 0, 0, 0, 0, 0, 1, 0, 2) {'total': 10, 'count': 1}
(1, 0, 0, 0, 0, 0, 1, 0, 2) {'total': 10, 'count': 1}
(1, 0, 0, 0, 0, 0, 1, 2, 2) {'total': 10, 'count': 1}
(1, 0, 0, 1, 0, 0, 1, 2, 2) {'total': 10, 'count': 1}
今回の対戦では"先手の勝ち"となっています。よって、この対戦の初手からの全ての盤面の合計値(total)に"10"を加算しています。また、1回の対戦のため回数(count)は全て"1"となっています。
keyで表した盤面の情報は(0, 0, 0, 0, 0, 0, 1, 0, 0)となっている部分です。この場合は6番目のマスに先手が手を打ったことを表しています。
この棋譜でのすべての得点付けの様子を以下に示します。
このように、最終結果が先手の勝ちにつながる盤面は加点し、負けにつながる盤面は減点する、という操作を対戦回数分だけ繰り返し、その結果を集計するという処理を行っています。そのため、各盤面は確率的に先手が勝てそうなほど高得点になります。ただし、対戦で現れた盤面の偏りで異常に高得点と判断してしまわないよう、回数も併せて記録し平均値で判断することを想定しています。
以上で盤面に得点を付ける処理の説明を終わります。
盤面から得点を予測する回帰式を決める
いよいよ本題の重回帰分析に入っていきます。ここまでで、曲がりなりにも各盤面に得点が付きました。これにより、どの手を打てば先手が勝てそうか(あるいは後手が勝てそうか)を予測するための材料が用意できたことになります。
ここではこの材料を加工して、重回帰分析ができるような回帰式の形を決めます。
重回帰分析とは
重回帰分析とは、ある結果を複数の原因から予測するモデルの事で、数式(回帰式)で以下のように表します。
$$\hat{y}=w_0x_0+w_1x_1 + w_2x_2 + \cdots + w_nx_n$$
重回帰分析の詳しい説明は、以下のサイトなどで後々見ていただくとして
今回作りたいのは、三目並べの結果を予測する回帰式です。もっと言うと、盤面の状態を元にその勝ちやすさを予測する回帰式をどうにかして作りたいです。
盤面のパターンに基づいた回帰式
今回は現在の盤面から、縦横斜めのパターン(手の配置状態)を抽出し説明変数とします。これらの説明変数から、目的変数である盤面の得点(平均値)を予測するという回帰式にしたいと思います。
順を追って見ていきます。
三目並べは、縦横斜めいずれか1列が揃った状態で勝ちが決まるルールです。これは、盤面全体を丸ごと見ずとも、縦横斜めの各列の手の配置がそれぞれどうなっているかを見れば、勝敗が判断できると言えそうです。
よって、このようなパターンを盤面から抜き出し回帰式に落とし込むことで、盤面の勝ちやすさが予測できるだろうと考えました。(と言っても、もともとはリバーシAIで既に確立された手法を見よう見まねで流用しただけですが…)
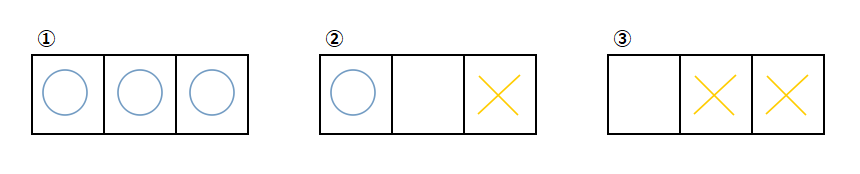
例えば、以下の3通りの状態があった場合、
先手にとっては① >>>>> ② > ③ の順で、より「勝つために重要だ!」と判断できそうです。今回使う重回帰分析で行う事は、このような「どの配置がどれぐらい重要か?」を表す重み($w$)について、棋譜の結果によく合うちょうどいい値を見つけ出す作業であると言えます。
それではより具体的に話を進めます。
盤面のパターン抽出
まず、現在の盤面から、以下の8パターンの配置を取得します。
(横)
横(水平方向)の状態を表すために、以下のh1、h2、h3の3列を抜き出します。
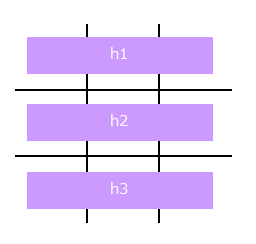
(縦)
縦(垂直方向)の状態を表すために、以下のv1、v2、v3の3列を抜き出します。
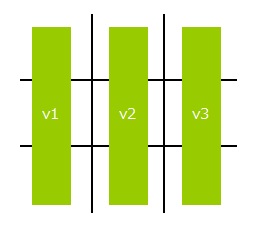
(斜め)
斜めの状態を表すために、以下のd1、d2の2列を抜き出します。
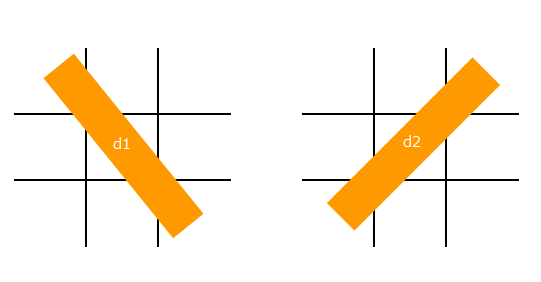
この時、各1列は3マスあり、1つのマス目は"空き" or "先手" or "後手"の3種類の状態を取り得ます。そして、その組み合わせは全部で3×3×3=27通りあります。今回の重回帰分析では、説明変数にこの8列×27通り=216個のパラメータを使って、目的変数である得点の予測を行う回帰式とします。
数式に直してみると、以下の様なイメージです。
$$\hat{y} = w_0 + w_1h1_0 + \cdots + w_{27}h1_{26} + w_{28}h2_0 + \cdots + w_{54}h2_{26} + w_{55}h3_0 + \cdots + w_{81}h3_{26} + w_{82}v1_0 + \cdots + w_{108}v1_{26} + w_{109}v2_0 + \cdots + w_{135}v2_{26} + w_{136}v3_0 + \cdots + w_{162}v3_{26} + w_{163}d1_0 + \cdots + w_{189}d1_{26} + w_{190}d2_0 + \cdots + w_{216}d2_{26}$$
この216個の説明変数($h1_{0~26}$・$h2_{0~26}$・$h3_{0~26}$・$v1_{0~26}$・$v2_{0~26}$・$v3_{0~26}$・$d1_{0~26}$・$d2_{0~26}$)はそれぞれ、現在の盤面のパターンに当てはまるものを"1"、当てはまらないものを"0"、として得点($\hat{y}$)を計算することを想定しています。
- $w_0$は切片
- $w_1, w_2, \cdots, w_{216}$は回帰係数(=各説明変数の重み)
回帰式に合わせたデータセットを作成する
それでは盤面の得点から、先ほどの回帰式に合うようデータセットを作成したいと思います。ここでいうデータセットとは、目的変数とすべての説明変数の対を集めたものを指します。また、作成したデータセットはcsvファイルに保存するものとします。
データセットを作成するプログラム
以下は、盤面の得点(scores)を元に、得点の平均値と盤面パターンのデータセットを作成し、csvファイルに出力するプログラムです。
得点の平均値が目的変数、その時の盤面パターンを示すパラメータが説明変数となります。プログラムを実行するとサンプルとして、10回、100回、1000回、10000回のランダムな打ち手の対戦結果から、それぞれのデータセットを作成します。
import itertools
import csv
from tictactoe import B, O, X
from scoring import RandomRecords
class Patterns:
def __init__(self, scores):
self.scores = scores
self.patterns = {
'h1': (0, 1, 2),
'h2': (3, 4, 5),
'h3': (6, 7, 8),
'v1': (0, 3, 6),
'v2': (1, 4, 7),
'v3': (2, 5, 8),
'd1': (0, 4, 8),
'd2': (2, 4, 6),
}
self.indexs = {}
def to_index(self, cells):
repeat = len(cells)
if repeat not in self.indexs:
product = enumerate(itertools.product([B, O, X], repeat=repeat))
self.indexs[repeat] = {j: i for i, j in product}
return self.indexs[repeat][cells]
def get_header(self):
header = ['ave']
for key, value in self.patterns.items():
header += [key + '-' + str(i) for i in range(3**len(value))]
return header
def get_dataset(self, board, score):
dataset = {'ave': score['total'] / score['count']}
for key, value in self.patterns.items():
pattern = tuple([board[i] for i in value])
if key not in dataset:
dataset[key] = [0 for _ in range(3**len(value))]
dataset[key][self.to_index(pattern)] = 1
return dataset
def to_csv(self, name):
with open(name, 'w', newline='') as f:
w = csv.writer(f)
header = self.get_header()
w.writerow(header)
scores = sorted(self.scores.items(),
key=lambda x: x[1]['total'] / x[1]['count'])
for board, score in scores:
dataset = self.get_dataset(board, score)
line = [dataset['ave']]
for key in self.patterns.keys():
line += dataset[key]
w.writerow(line)
if __name__ == '__main__':
rand = RandomRecords()
for num in [10, 100, 1000, 10000]:
name = 'rand' + str(num) + '.csv'
print(f'\n[{name}]')
scores = rand.scoring(num)
patterns = Patterns(scores)
patterns.to_csv(name)
(実行方法)
python dataset.py
(実行結果)
[rand10.csv]
O = 6/10 (60.0%)
X = 4/10 (40.0%)
D = 0/10 (0.0%)
[rand100.csv]
O = 55/100 (55.0%)
X = 33/100 (33.0%)
D = 12/100 (12.0%)
[rand1000.csv]
O = 584/1000 (58.4%)
X = 301/1000 (30.1%)
D = 115/1000 (11.5%)
[rand10000.csv]
O = 5846/10000 (58.5%)
X = 2808/10000 (28.1%)
D = 1346/10000 (13.5%)
対戦結果の勝率を表示し、実行フォルダにそれぞれcsvファイル(rand{対戦回数}.csv)が作成されます。
続いて、プログラムの中身を説明していきます。
パターンの設定
縦横斜めのパターンをpatternsに設定しています。中身は、各列のパターン名をキー、対応するマス目の番号の組(タプル)を値、とした辞書型のデータとしています。
class Patterns:
def __init__(self, scores):
self.scores = scores
self.patterns = {
'h1': (0, 1, 2),
'h2': (3, 4, 5),
'h3': (6, 7, 8),
'v1': (0, 3, 6),
'v2': (1, 4, 7),
'v3': (2, 5, 8),
'd1': (0, 4, 8),
'd2': (2, 4, 6),
}
self.indexs = {}
(マス目の番号)
0|1|2
-+-+-
3|4|5
-+-+-
6|7|8
パターンをインデックスに変換
各パターンの3マスの状態を元に、0~26のインデックスに変換します。このインデックスは、3×3×3=27通りある組み合わせの、いずれに該当するかを示すためのものです。
import itertools
from tictactoe import B, O, X
class Patterns:
def to_index(self, cells):
repeat = len(cells)
if repeat not in self.indexs:
product = enumerate(itertools.product([B, O, X], repeat=repeat))
self.indexs[repeat] = {j: i for i, j in product}
return self.indexs[repeat][cells]
(各パターンのインデックス)
(0, 0, 0): 0,
(0, 0, 1): 1,
(0, 0, 2): 2,
(0, 1, 0): 3,
(0, 1, 1): 4,
(0, 1, 2): 5,
(0, 2, 0): 6,
(0, 2, 1): 7,
(0, 2, 2): 8,
(1, 0, 0): 9,
(1, 0, 1): 10,
(1, 0, 2): 11,
(1, 1, 0): 12,
(1, 1, 1): 13,
(1, 1, 2): 14,
(1, 2, 0): 15,
(1, 2, 1): 16,
(1, 2, 2): 17,
(2, 0, 0): 18,
(2, 0, 1): 19,
(2, 0, 2): 20,
(2, 1, 0): 21,
(2, 1, 1): 22,
(2, 1, 2): 23,
(2, 2, 0): 24,
(2, 2, 1): 25,
(2, 2, 2): 26
該当する列の手の状態が下図の場合、インデックスは11となります。
本メソッドは3マスだけでなく、4マスなどでも対応できるよう作ったつもりです。パターンの設定をいろいろ変えてみると、もっと良い方法が見つかるかもしれません。
データセットをcsvファイル形式で出力
盤面の得点を集計した結果から、得点の平均値を算出し目的変数aveとします。平均値は単純に、集計した得点のtotal/countで求めています。また各説明変数は、盤面パターンに該当するもを"1"、そうでないものを"0"とします。そうして作成したデータ(目的変数と説明変数の対)を、1行ずつcsvファイルに出力します。
なお、csvファイルの一行目には各変数名の見出しを出力しています。見出しの作成はget_headerにて行います。
import csv
class Patterns:
def get_header(self):
header = ['ave']
for key, value in self.patterns.items():
header += [key + '-' + str(i) for i in range(3**len(value))]
return header
def get_dataset(self, board, score):
dataset = {'ave': score['total'] / score['count']}
for key, value in self.patterns.items():
pattern = tuple([board[i] for i in value])
if key not in dataset:
dataset[key] = [0 for _ in range(3**len(value))]
dataset[key][self.to_index(pattern)] = 1
return dataset
def to_csv(self, name):
with open(name, 'w', newline='') as f:
w = csv.writer(f)
header = self.get_header()
w.writerow(header)
scores = sorted(self.scores.items(),
key=lambda x: x[1]['total'] / x[1]['count'])
for board, score in scores:
dataset = self.get_dataset(board, score)
line = [dataset['ave']]
for key in self.patterns.keys():
line += dataset[key]
w.writerow(line)
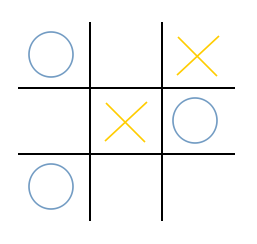
試しに、以下の盤面から説明変数を抜き出す場合を考えてみます。
h1の場合、一番上の横列が該当します。
この部分の手の状態を抜き出してインデックスに変換した場合、先に示したとおり11となります。
各列には27個の説明変数が用意されていますが、インデックスはどの説明変数に該当するかを示すための値です。
インデックスに該当する説明変数は"1"とし、その他は該当なしの意味で"0"とすることで、特定の盤面に対する得点を表現した回帰式を実現しています。
結果として、h1の説明変数27個の値は以下となります。
# (O, B, X): 11
h1 = [0, 0, 0, 0, 0, 0, 0, 0, 0, # 0 - 8
0, 0, 1, 0, 0, 0, 0, 0, 0, # 9 - 17
0, 0, 0, 0, 0, 0, 0, 0, 0] # 18 - 26
同様にすると、全部の説明変数は以下のイメージになります。
# (O, B, X): 11
h1 = [0, 0, 0, 0, 0, 0, 0, 0, 0, # 0 - 8
0, 0, 1, 0, 0, 0, 0, 0, 0, # 9 - 17
0, 0, 0, 0, 0, 0, 0, 0, 0] # 18 - 26
# (B, X, O): 7
h2 = [0, 0, 0, 0, 0, 0, 0, 1, 0, # 0 - 8
0, 0, 0, 0, 0, 0, 0, 0, 0, # 9 - 17
0, 0, 0, 0, 0, 0, 0, 0, 0] # 18 - 26
# (O, B, B): 9
h3 = [0, 0, 0, 0, 0, 0, 0, 0, 0, # 0 - 8
1, 0, 0, 0, 0, 0, 0, 0, 0, # 9 - 17
0, 0, 0, 0, 0, 0, 0, 0, 0] # 18 - 26
# (O, B, O): 10
v1 = [0, 0, 0, 0, 0, 0, 0, 0, 0, # 0 - 8
0, 1, 0, 0, 0, 0, 0, 0, 0, # 9 - 17
0, 0, 0, 0, 0, 0, 0, 0, 0] # 18 - 26
# (B, X, B): 6
v2 = [0, 0, 0, 0, 0, 0, 1, 0, 0, # 0 - 8
0, 0, 0, 0, 0, 0, 0, 0, 0, # 9 - 17
0, 0, 0, 0, 0, 0, 0, 0, 0] # 18 - 26
# (X, O, B): 21
v3 = [0, 0, 0, 0, 0, 0, 0, 0, 0, # 0 - 8
0, 0, 0, 0, 0, 0, 0, 0, 0, # 9 - 17
0, 0, 0, 1, 0, 0, 0, 0, 0] # 18 - 26
# (O, X, B): 15
d1 = [0, 0, 0, 0, 0, 0, 0, 0, 0, # 0 - 8
0, 0, 0, 0, 0, 0, 1, 0, 0, # 9 - 17
0, 0, 0, 0, 0, 0, 0, 0, 0] # 18 - 26
# (X, X, O): 25
d2 = [0, 0, 0, 0, 0, 0, 0, 0, 0, # 0 - 8
0, 0, 0, 0, 0, 0, 0, 0, 0, # 9 - 17
0, 0, 0, 0, 0, 0, 0, 1, 0] # 18 - 26
これを回帰式に直すと、以下になります。
$$\hat{y} = w_{0} + w_{12}h1_{11} + w_{35}h2_{7} + w_{64}h3_{9} + w_{92}v1_{10} + w_{115}v2_{6} + w_{157}v3_{21} + w_{178}d1_{15} + w_{215}d2_{25}$$
実はほとんどの説明変数は"0"となり、式からは消えてしまいます。
さらには、該当するパターンの説明変数は"1"でしたので、結局は次の式のように切片と重みの合計値で得点の予測値が決まることになります。
$$\hat{y} = w_{0} + w_{12} + w_{35} + w_{64} + w_{92} + w_{115} + w_{157} + w_{178} + w_{215}$$
このような、各パターン毎に用意した27種類の説明変数のいずれかが"1"でそれ以外を"0"とするような作りを、one-hot表現と呼ぶそうです。
プログラム実行後の、csvファイルの出力結果は以下のようになります。
一番左のaveが目的変数となる得点の平均値、その他が説明変数となる盤面を表すパラメータです。
以上でデータセットの作成は完了です。次はいよいよ山場となる重回帰分析に移ります。
データセットを重回帰分析し回帰式を求める
データセットを重回帰分析して、目的変数を予測するための回帰式(切片$w_o$と各重み$w_{1}$~$w_{216}$の値)を求めます。
重回帰分析プログラム
重回帰分析を行うクラスとしてRegressionを用意しました。
本クラスは初期化時のタイミングで、まずcsvファイルを読み込みデータセットを取得します。次に、目的変数のaveをyに設定し、説明変数をxに設定します。そして、scikit-learnの線形回帰分析クラスであるLinearRegression用いて、fitメソッドにより重回帰分析を実施します。
import pandas as pd
from sklearn.linear_model import LinearRegression
from dataset import Patterns
class Regression:
def __init__(self, csv, show=True):
dataset = pd.read_csv(csv)
dataset_except_ave = dataset.drop('ave', axis=1)
x = dataset_except_ave.values
y = dataset['ave'].values
self.model = LinearRegression()
self.model.fit(x, y)
self.p = Patterns(None)
self.show = show
求めた回帰式はself.modelに保持されています。データセットさえ作ってしまえば、あとはfitするだけの簡単なお仕事でした。scikit-learnとても便利です!!
回帰式を使って得点予測するAIを作る
続いて、先ほどのRegressionクラスに、盤面の得点を予測し手を打つ処理を追加します。これにより、実際に対戦可能なAIが完成となります。
得点予測プログラム
以下は指定されたデータセットを重回帰分析し、求めた回帰式から盤面の得点予測を行うプログラムです。
import pandas as pd
from sklearn.linear_model import LinearRegression
from tictactoe import TicTacToe, B, O, rand
from dataset import Patterns
class Regression:
def __init__(self, csv, show=True):
dataset = pd.read_csv(csv)
dataset_except_ave = dataset.drop('ave', axis=1)
x = dataset_except_ave.values
y = dataset['ave'].values
self.model = LinearRegression()
self.model.fit(x, y)
self.p = Patterns(None)
self.show = show
def _print(self, *args):
if self.show:
print(*args)
def to_x(self, board):
x = []
for key, value in self.p.patterns.items():
state = tuple([board[i] for i in value])
patterns = [0 for _ in range(3**len(value))]
patterns[self.p.to_index(state)] = 1
x += patterns
return [x]
def move(self, board, turn):
blank = [i for i, cell in enumerate(board) if cell == B]
index, score = None, 0
self._print()
for i in blank:
board[i] = turn
predict = self.model.predict(self.to_x(board))[0]
cond = predict > score if turn == O else predict < score
if index is None or cond:
index, score = i, predict
self._print(i, '=', predict)
board[i] = B
self._print('move :', index)
return index
if __name__ == '__main__':
num = 1000
for name in ['rand10.csv', 'rand100.csv', 'rand1000.csv', 'rand10000.csv']:
model = Regression(name, show=False)
print(f'\n[{name}]')
print('--- O ---')
TicTacToe(model.move, rand).simulate(num)
print('--- X ---')
TicTacToe(rand, model.move).simulate(num)
実行するとサンプルとして、ランダムな打ち手との対戦結果(勝率)を表示します。対戦回数は1000回です。重回帰分析に用いるデータセットに10戦、100戦、1000戦、10000戦を用いた場合の結果をそれぞれ表示します。
(実行方法)
python regression.py
(実行結果)
[rand10.csv]
--- O ---
O = 594/1000 (59.4%)
X = 223/1000 (22.3%)
D = 183/1000 (18.3%)
--- X ---
O = 502/1000 (50.2%)
X = 392/1000 (39.2%)
D = 106/1000 (10.6%)
[rand100.csv]
--- O ---
O = 757/1000 (75.7%)
X = 76/1000 (7.6%)
D = 167/1000 (16.7%)
--- X ---
O = 354/1000 (35.4%)
X = 576/1000 (57.6%)
D = 70/1000 (7.0%)
[rand1000.csv]
--- O ---
O = 953/1000 (95.3%)
X = 14/1000 (1.4%)
D = 33/1000 (3.3%)
--- X ---
O = 73/1000 (7.3%)
X = 879/1000 (87.9%)
D = 48/1000 (4.8%)
[rand10000.csv]
--- O ---
O = 990/1000 (99.0%)
X = 0/1000 (0.0%)
D = 10/1000 (1.0%)
--- X ---
O = 44/1000 (4.4%)
X = 913/1000 (91.3%)
D = 43/1000 (4.3%)
対戦回数が多いデータセットを用いるほど、勝率(予測の精度)が上がることが確認できます。今回は実施しませんでしたが、データセットの作成時に、盤面の回転形(90°、180°、270°)や対称形(0°、45°、90°、135°)を同時に生成し、かさ増しすることで、より少ない対戦数で勝率が上がることが予想されます。
プログラムの中身の説明を続けます。
評価値表示の切換
初期化時の引数showは、メッセージを表示するかどうかを切り替えます。
Trueとしておくと、AIが予測した得点が表示されます。対戦プレイ時にAIがどのように盤面を見ているかを確認する際に使用します。また、対戦シミュレーション時など表示が不要な場合は、Falseとして下さい。
class Regression:
def __init__(self, csv, show=True):
:
self.show = show
def _print(self, *args):
if self.show:
print(*args)
現在の盤面を目的変数に変換
回帰式を使って得点を予測するためには、データセット(csvファイル)の目的変数と同じ形式のデータが必要になります。to_xメソッドにて、入力された盤面を目的変数の形式に変換します。
class Regression:
def to_x(self, board):
x = []
for key, value in self.p.patterns.items():
state = tuple([board[i] for i in value])
patterns = [0 for _ in range(3**len(value))]
patterns[self.p.to_index(state)] = 1
x += patterns
return [x]
回帰式を使って得点予測
現在の手番で打てる候補について、先手番の場合は最も盤面の得点が高くなる手を選びます。また、後手番の場合は最も得点が低くなる手を選びます。
得点の予測にはLinearRegressionクラスのpredictメソッドを実施します。引数には盤面を目的変数の形式に変換したものを入れます。
from tictactoe import B, O
class Regression:
def move(self, board, turn):
blank = [i for i, cell in enumerate(board) if cell == B]
index, score = None, 0
self._print()
for i in blank:
board[i] = turn
predict = self.model.predict(self.to_x(board))[0]
cond = predict > score if turn == O else predict < score
if index is None or cond:
index, score = i, predict
self._print(i, '=', predict)
board[i] = B
self._print('move :', index)
return index
空いているマスにそれぞれ手を打ってみて盤面の得点を算出し、最も良い手を最終結果として返しています。
scikit-learnの使い勝手としては、fitして作成したモデル(回帰式)をpredictで使う、というごくシンプルなものでした。
作ったAIと対戦するプログラムを実装する
最後に重回帰分析して作ったAIと対戦してみましょう。以下は1万回の棋譜で学習したAIとの対戦用プログラムです。
from tictactoe import TicTacToe, user
from regression import Regression
if __name__ == '__main__':
turn = None
while True:
turn = input('select your player O or X > ')
if turn == 'O' or turn == 'X':
break
if turn == 'O':
TicTacToe(user, Regression('rand10000.csv').move).play()
else:
TicTacToe(Regression('rand10000.csv').move, user).play()
(実行方法)
> python ml_tictactoe.py
データセットの読み込みには数十秒程度の時間がかかる場合がありますので、しばらくお待ちください。
(遊び方)
最初に、"O" or "X"を入力して自身の手番を設定します。その後は今までと同じように遊べます。
select your player O or X >
対戦の際は以下のように、AIが評価した手の得点が表示されます。
O| |
-+-+-
| |
-+-+-
| |
turn : X
1 = 4.15625
2 = 4.28125
3 = 4.96875
4 = 1.671875
5 = 4.5234375
6 = 4.859375
7 = 4.4921875
8 = 3.4453125
move : 4
O| |
-+-+-
|X|
-+-+-
| |
今回のAIは、後手番ではより得点の低い手を選ぶようにしています。これは盤面の得点を決める際に、"先手番が勝つほど加点"し"後手番が勝つほど減点"するようにしたためです。
上記の局面でAIは「最も得点の低かった4(真ん中)が勝てそうだ」と踏み、その手を選んでいることが確認できます。
後手番は対ランダム戦で勝率91%との結果が出ていましたが、実際に対戦してみると穴だらけで実はまだまだ弱かったです…。
おわりに
今まで三目並べの実装例として、MinMax法や深層強化学習といった手法は見たことがあったのですが、重回帰分析を用いた手法は見つからず、個人的な興味でトライしてみました。
当初は重回帰分析ってどうやるんだ??と身構えていましたが、いざやってみるとscikit-learnが拍子抜けするほど簡単にやってくれました。
今回の実装を通して割と単純なモデルでもそれなりのAIが作れる事が分かり、重回帰分析をどう使うかのイメージは十分掴めたかなと思います。とはいえ、背後にあるモデルの妥当性など本質的な部分の理解が足りず、もっと精進が必要だと感じました。実際、後手番の勝率を上げようと得点の付け方や縦横斜めのパターン以外を試行錯誤してみたのですが、より良い指針が見い出せなかったです。
当方まだまだ勉強中の身のため、記載内容に不備などたくさんあるかと思いますが、お気づきの際は遠慮なくご指摘いただけると大変有難く思います。
最後までお読みいただきありがとうございました。
なお、今回作成したソースコードは以下に置いております。良かったらチェックしてみて下さい。