今回は Ridge 回帰の実装(コード)をまとめていきます。
■ Ridge回帰の手順
次の7つのSTEPで進めます。
- モジュールの用意
- データの準備
- パラメータの探索
- モデルの作成
- 予測値の算出
- 残差プロット
- モデルの評価
1. モジュールの用意
最初に、必要なモジュールをインポートしておきます。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# データセットを読み込むモジュール
from sklearn.datasets import load_boston
# 訓練データとテストデータを分割するモジュール
from sklearn.model_selection import train_test_split
# 標準化(分散正規化)を行うモジュール
from sklearn.preprocessing import StandardScaler
# パラメータ(alpha)を探索するモジュール
from sklearn.linear_model import RidgeCV
# パラメータ(alpha)をプロットするモジュール
from yellowbrick.regressor import AlphaSelection
# Ridge 回帰を実行するモジュール(最小二乗法+L2正則化項)
from sklearn.linear_model import Ridge
## 2. データの準備 データの取得をした後、処理しやすいように分割を行います。
# Bostonデータセットの読み込み
boston = load_boston()
# 目的変数と説明変数に分ける
X, y = boston.data, boston.target
# 標準化(分散正規化)
SS = StandardScaler()
X = SS.fit_transform(X)
# 訓練データとテストデータに分割する
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, random_state=123)
標準化は、例えば2桁と4桁の特徴量(説明変数)があった際に、後者の影響が大きくなってしまうため
全ての特徴量に対して平均を0・分散を1にして、スケールを揃えています。
random_state では、データの分割結果が毎回同じになるようにシード値を固定しています。
3. パラメータの探索
Ridge 回帰では過学習を避けるために、最小二乗法の式に正則化項が追加されています。
alpha を大きくすると正則化が強くなり、小さくすると弱くなります。
最適な alpha を求めるため、訓練データに対してグリッドサーチと交差検証を行います。
# パラメータ(alpha)の探索区間を設定
alphas = np.logspace(-10, 1, 500)
# 訓練データを交差検証し、最適な alpha を求める
ridgeCV = RidgeCV(alphas = alphas)
# alpha をプロットする
visualizer = AlphaSelection(ridgeCV)
visualizer.fit(X_train, y_train)
visualizer.show()
plt.show()
<出力結果>
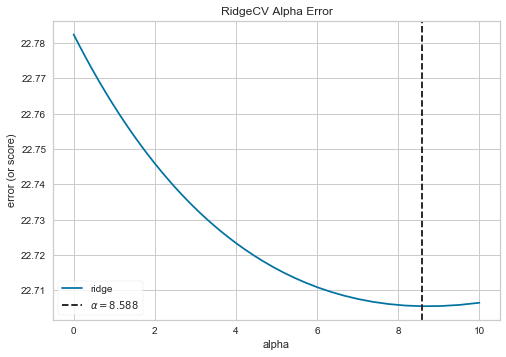
以上より、最適な alpha = 8.588 が求まりました。
4. モデルの作成
先ほど求めたパラメータ(alpha)を用いて、Ridge 回帰のモデルを作成していきます。
# Ridge回帰のインスタンスを作成
ridge = Ridge(alpha = 8.588)
# 訓練データからモデルを生成(最小二乗法+正則化項)
ridge.fit(X_train, y_train)
# 切片を出力
print(ridge.intercept_)
# 回帰係数(傾き)を出力
print(ridge.coef_)
<出力結果>
lr.intercept_: 22.564747201001634
lr.coef_: [-0.80818323 0.81261982 0.24268597 0.10593523 -1.39093785 3.4266411
-0.23114806 -2.53519513 1.7685398 -1.62416829 -1.99056814 0.57450373
-3.35123162]
lr.intercept_:切片(重み $w_0$)
lr.coef_:回帰係数・傾き(重み $w_1$ ~ $w_{13}$)
よって、モデル式(回帰式)における具体的な数値が求まりました。
$ y = w_0 + w_1x_1+w_2x_2+ \cdots + w_{12}x_{12} + w_{13}x_{13}$
5. 予測値の算出
作成したモデル式にテストデータ(X_test)を入れ、予測値(y_pred)を求めます。
y_pred = lr.predict(X_test)
y_pred
<出力結果>
y_pred: [15.25513373 27.80625237 39.25737057 17.59408487 30.55171547 37.48819278
25.35202855 ..... 17.59870574 27.10848827 19.12778747 16.60377079 22.13542152]
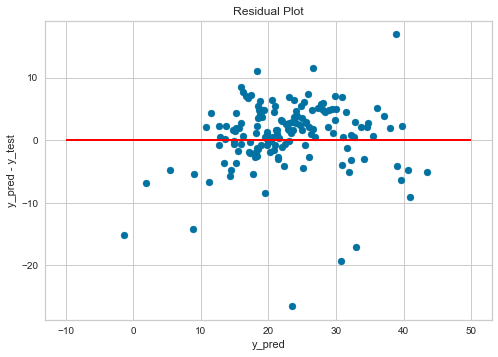
## 6. 残差プロット モデルの評価をする前に、残差のプロットを見ておきます。
残差:予測値と正解値の差(y_pred - y_test)
# 描画オブジェクトとサブプロットの作成
fig, ax = plt.subplots()
# 残差のプロット
ax.scatter(y_pred, y_pred - y_test, marker = 'o')
# y = 0 の赤い直線をプロット
ax.hlines(y = 0, xmin = -10, xmax = 50, linewidth = 2, color = 'red')
# 軸ラベルを設定する
ax.set_xlabel('y_pred')
ax.set_ylabel('y_pred - y_test')
# グラフのタイトルを追加
ax.set_title('Residual Plot')
plt.show()
赤い線(y_pred - y_test = 0)の上と下で、バランス良くデータが散らばっているので
予測値の出力に大きな偏りはないことが確認できます。
7. モデルの評価
今回は、決定係数を用いて評価をしていきます。
# 訓練データに対するスコア
print(ridge.score(X_train, y_train))
# テストデータに対するスコア
print(ridge.score(X_test, y_test))
<出力結果>
Train Score: 0.763674626990198
Test Score: 0.6462122981958535
## ■ 最後に 以上、上記1~7の手順に沿って、Ridge 回帰を行いました。
今回は初学者の方向けに、実装(コード)のみまとめさせていただきましたが
今後タイミングを見て、理論(数式)についても記事を作成していければと思います。
ご精読いただき、ありがとうございました。
参考文献:Pythonによるあたらしいデータ分析の教科書
(Python 3 エンジニア認定データ分析試験 主教材)