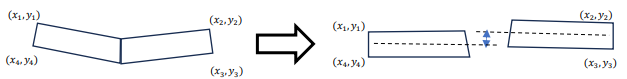レシート上の要素に対する領域ごとの角度補正
前回までの概要
レシートの要素の行の判別を行うために、座標を利用して同じ行のグループ化をおこないました。
その際にレシートが斜めになっている場合を考慮して、要素の傾きによって全体を回転させることで、
より多くの要素を水平にし、行の判別をより正確にできました。
前回ページはこちらから確認ください!
今回の背景
現実問題として、レシートは保管が難しく撮影し、OCRに読み込ませる際には、
折れ曲がっている場合があります。これを正確に読み取り,行の判別を行うのはかなり難しいです。
今回はその折れ線によって分割された領域ごとに、別の回転や移動を適応することで、
より精度の高い行のグループ化が実現できるかどうかを検討します。
今回与えられたタスクと課題
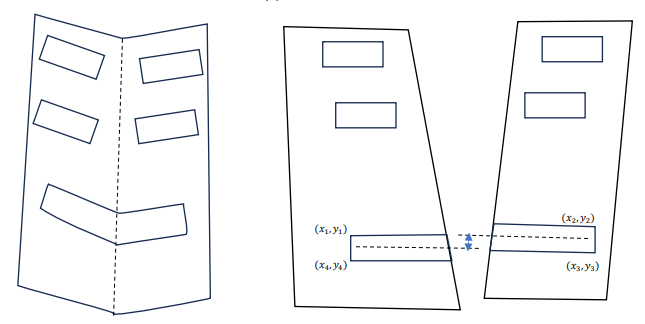
レシートの要素の中に、レシートの左端から右端までまたがるような、大きい要素に注目しました。
レシートが縦に折れ曲がっているとき、この要素も折れ曲がっている可能性が高いと考えられます。
レシートの折れ曲がりによって生まれる、y座標の変化をある程度検出するために、
この大きい要素を利用します。今回はレシートに折れ曲がりが、
一つあることを前提として検証しました。一つの大きい要素を、
折れ曲がりの右側と左側で別に回転させ、回転後の差を得ることで、
全体の折れ曲がりによる差分を取得したいと考えました。

大きな要素を左右別々に回転させる
前回要素全体の平均傾きを利用して、傾きを0に近づけるというアプローチで回転させましたが、
それでは左右を別々で回転することはできません。また、全体を同時に回転させていました。
今回はレシート内で幅が一番大きい要素に対し、縦の辺を垂直にするという
アプローチで回転させることで、左右を別々に回転させることを考えました。
要素の四頂点の座標を$ (𝑥_1, 𝑦_1)~(𝑥_4, 𝑦_4) $として回転角を求めていきます。まず、右の要素の傾きrightAngleを求めます。
$$ rightAngle = \frac{y_3-y_2}{x_3-x_2} $$
次に回転角を求めます。回転角を𝜃、要素の中心座標を$ (𝐶_𝑥, 𝐶_𝑦) $とし、回転させたい座標を
$ (𝑥, 𝑦) $とすると、三角関数を用いた計算方法は次のようになります。
$$
\theta = 90-tan^{-1}(angle)
$$
$$
\hat{y} = C_x + (x-C_x) * \cos{\theta} - (y-C_y) * \sin{\theta}
$$
$$
\hat{y} = C_y + (x-C_x) * \sin{\theta} + (y-C_y) * \cos{\theta}
$$
左の要素の傾きleftAngleはrightAngleを次のようにして三角関数を適応すればよいだけです。
$$
leftAngle = \frac{y_4-y_1}{x_4-x_1}
$$
ここまでが、傾きを垂直、つまり 90 度に近づけるための要素の回転方法です。
次に左右の要素の y 座標の差を取得します。右の縦の辺を基準に要素を回転したものを
leftBoundingbox、左を基準に回転したものをrightBoundingboxとし、中間座標を求めます。
左の中間座標はleftBoundingboxの$ ((𝑥_1 + 𝑥_4)/2, (𝑦_1 + 𝑦_4)/2) $、
右の中間座標はrightBoundingboxの$ ((𝑥_2 + 𝑥_3)/2, (𝑦_2 + 𝑦_3)/2) $で求められるので、
これよりy座標の差diffは$ (𝑦_1 + 𝑦_4)/2 − (𝑦_2 + 𝑦_3)/2 $となります。
全体の補正
先ほど求めた回転角とy座標の差を、右寄りの要素と左寄りの要素に対して、
それぞれ適応していきたいと思います。初めに、その右寄りの要素とするか、
左寄りとするかの条件付けを行っていきます。
まず、すべての要素の横幅を取得し、横幅が一番大きい要素の60%以下かつ、
左端のx座標が一番大きい要素の横幅の+-20%以内であれば左寄りの要素とします。
右寄りの要素も同様の条件で右端の座標で比較します。
ただし、ここでの閾値の%の値は必要に応じて変更し、最適な値を模索していきます。
これにより振り分けられた右寄りの要素と、左寄りの要素をそれぞれ
rightAngleとleftAngleで回転し、右寄りの要素のy座標にdiffを足します。
そうすることで回転によって生じたy座標のずれが軽減されることを期待しています。
最後に
今回まとめた方法の具体的な実装は、次回以降にまとめていく予定です。
また、これらを利用したOCRは、LINEからどなたでも無料でご利用いただけますので、
ぜひ試してください!
また、OCRのでも体験がこちらのページからできます!