概要
AWS資格試験受験(AWS Certified Machine Learning Engineer - Associate)のために、せっかく機械学習に関して学ぶなら手を動かしながら学びたいと思い、SageMaker Studio Labを使用し、ロジスティック回帰分析を用いて、機械学習モデルの構築を行ってみた記事になります。
なお実業務では機械学習モデルの構築は一切行ったことがないため、誤りなどございましたらご指摘ください。
ロジスティック回帰とは
一言で言うならば、ロジスティック回帰は、分類問題(※)に使われる機械学習の手法の一つです。回帰という名前がついていますが、特に二値分類(例:はい・いいえ/合格・不合格 など)の際に使用されます。
※分類問題とは
データをいくつかのカテゴリーやクラスに分ける(分類する)ことを目的とする機械学習のタスクのことです。与えられたデータが、どのグループに属するかを予測する際、「分類」という用語を使用します。
実行環境
SageMaker Studio Labを使用しました。
SageMaker Studio Labとは、AWSが提供する、AWSアカウント不要でJupiter Notebookを使用できるサービスのことです。※アカウント作成方法の説明については省略いたします。
- conda (4.10.3)で仮想環境を作成して検証
- ブラウザ:Edgeで実施
- 端末: Mac
今回やってみたこと
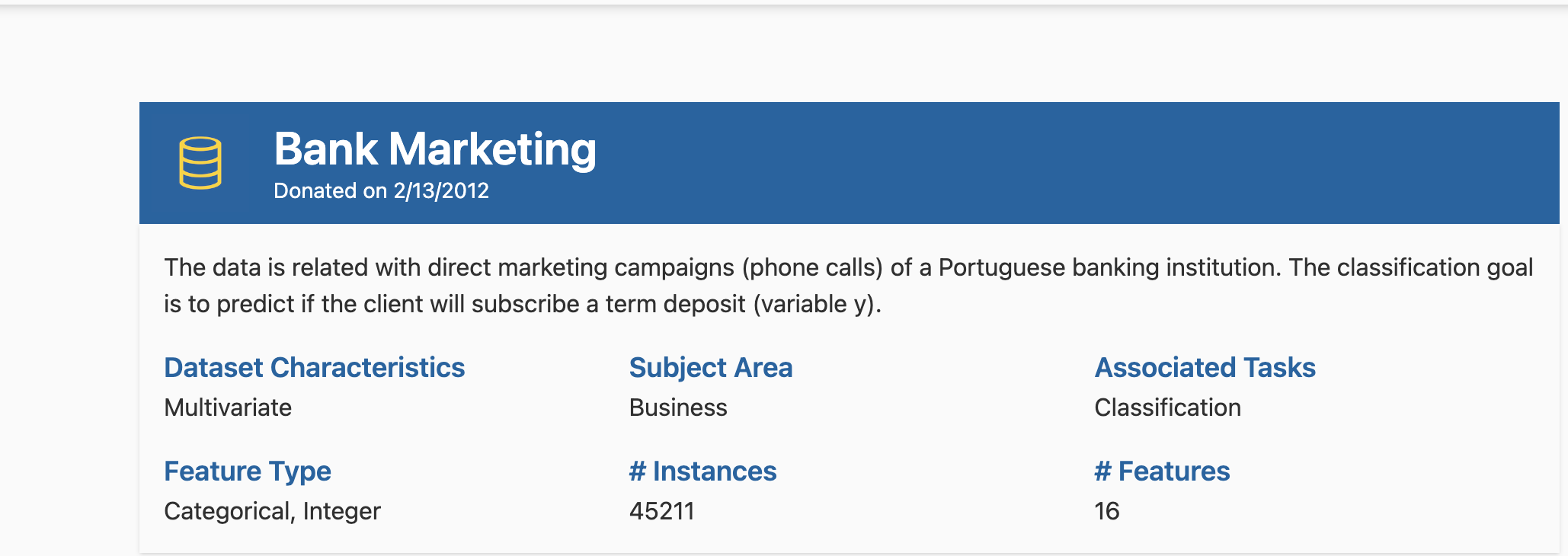
UC Irvine Machine Learning Repositoryという、機械学習向けのデータセットが公開されているサイトのデータを使い、簡単な機械学習モデルを作ってみました。
使用したデータセットは、Bank Marketingというデータで、ポルトガルの銀行機関のダイレクトマーケティングキャンペーンに関する情報で、顧客が定期預金を申し込んだかどうかや、顧客の属性(年齢や職業)に関するデータが格納されています。
The classification goal is to predict if the client will subscribe a term deposit (variable y).
データセットにも記載がありましたが、その顧客が定期預金を申し込むかどうかを予測するのが目的です。
データセットの中身
分析には、bank.csvというデータを使いました。
まずは、データセットの中身に何が入っているのか確認をしてみます。
顧客の年齢や職業などの顧客の属性に関する情報、顧客への連絡手段や日時など、マーケティング施策の結果に関する情報などが入っています。
| 変数名 | 役割 | データの 種類 |
説明 |
|---|---|---|---|
| age | Feature | Integer | 年齢 |
| job | Feature | Categorical | 職業 |
| marital | Feature | Categorical | 婚姻状況(既婚/離婚/独身) |
| education | Feature | Categorical | 不明/初等教育/中等/高等教育 |
| default | Feature | Binary | クレジットデフォルト(債務不履行)の有無 |
| balance | Feature | Integer | 残高(年間平均残高、単位は€) |
| housing | Feature | Binary | 住宅ローンの有無 |
| loan | Feature | Binary | 個人のローンの有無 |
| contact | Feature | Categorical | 顧客へ最後に連絡した際の連絡手段 (不明/電話/携帯) |
| day_of_week | Feature | Date | 最後に連絡した日付 |
| month | Feature | Date | 最後に連絡した月 |
| duration | Feature | Integer | 連絡時間(顧客とどれだけ長く電話をしているか) |
| campaign | Feature | Integer | 顧客への連絡回数 |
| pdays | Feature | Integer | 前回のキャンペーンからの経過日数 |
| previous | Feature | Integer | 現在のキャンペーン前の、顧客への連絡回数 |
| poutcome | Feature | Categorical | 前回のマーケティングキャンペーンの結果 |
| y | Target | Binary | 顧客が定期預金を購入したかどうか |
予測スタート
データのインポート、欠損値の確認
まずはデータ加工のpythonライブラリpandasを使ってデータをインポートします。
import pandas as pd
data = pd.read_csv('bank.csv', sep=';')# csvファイルへのパスは適宜置き換えてください
data.head()
data.head()
で先頭5行のデータを見ることができます。なお、引数のsepは、csvの区切り文字の指定を表しています。

さらに、
data.isnull().sum()
で、特徴量(※)ごとに欠損値があるデータの個数を調べることができます。
ここで欠損値があるならば、補完する値をどうするか考慮する必要がありますが、幸い今回は欠損データがなさそうです。
※特徴量とは予測の手掛かりとなる変数のことを指します。
age 0
job 0
marital 0
education 0
default 0
balance 0
housing 0
loan 0
contact 0
day 0
month 0
duration 0
campaign 0
pdays 0
previous 0
poutcome 0
y 0
dtype: int64
データの前処理
データをインポートして、そのまま予測できる、と言うわけには残念ながらいきません。
データの前処理が必要となります。そこで、具体的にはどういった前処理が必要になるのか整理してみました。様々な前処理がありますが、どれも共通してモデルがデータを数値的に理解しやすいようにすることが目的となっています。
ターゲット変数の数値化
予測する対象が「yes/no」「成功/失敗」など文字列のデータとなっている場合、モデルが値を扱うことができるように0・1の数値に変換する必要があります。
# ターゲット変数を 'y' に設定し、数値化
data['y'] = data['y'].apply(lambda x: 1 if x == 'yes' else 0)
この部分で、yカラムの値に関して、yes ・noの2値で表現されているのを、1・0の2値に変換しています。
カテゴリ変数の数値化(ダミー変数化)
カテゴリ変数とは、文字列やラベルとして表現されるデータのことです。
文字列やラベルは、そのままでは機械学習モデルが扱えないため、0・1などの数値に変換する必要があります。
その手法として、ワンホットエンコーディング・ダミーエンコーディングなどがあります。
今回の実装では、ダミーエンコーディングを行っています。
# カテゴリ変数をダミー変数に変換
data_encoded = pd.get_dummies(data, drop_first=True)
# エンコード後の特徴量を確認
print("エンコード後の特徴量名:")
print(data_encoded.columns)
#結果
Index(['age', 'balance', 'day', 'duration', 'campaign', 'pdays', 'previous',
'y', 'job_blue-collar', 'job_entrepreneur', 'job_housemaid',
'job_management', 'job_retired', 'job_self-employed', 'job_services',
'job_student', 'job_technician', 'job_unemployed', 'job_unknown',
'marital_married', 'marital_single', 'education_secondary',
'education_tertiary', 'education_unknown', 'default_yes', 'housing_yes',
'loan_yes', 'contact_telephone', 'contact_unknown', 'month_aug',
'month_dec', 'month_feb', 'month_jan', 'month_jul', 'month_jun',
'month_mar', 'month_may', 'month_nov', 'month_oct', 'month_sep',
'poutcome_other', 'poutcome_success', 'poutcome_unknown'],
dtype='object')
ワンホットエンコーディング
全てのカテゴリ変数を独立した特徴量に変換する手法のことです。
今回のデータセットを使って説明するならば、marital(婚姻状況)カラムを、下記のような形で表現することができます。
| 婚姻状況 | 結婚(marital_married) | 独身(marital_single) | 離婚(marital_divorced) |
|---|---|---|---|
| 結婚 | 1 | 0 | 0 |
| 独身 | 0 | 1 | 0 |
| 離婚 | 0 | 0 | 1 |
ダミーエンコーディング
ワンホットエンコーディングのうち、1つのカテゴリを削除した手法のことです。上記の例を使うならば、
省略されたカテゴリ離婚(marital_divorced)は、他のカテゴリが全て0となる場合に該当します。
| 婚姻状況 | 結婚(marital_married) | 独身(marital_single) |
|---|---|---|
| 結婚 | 1 | 0 |
| 独身 | 0 | 1 |
| 離婚 | 0 | 0 |
特徴量とターゲット変数の分離
予測に使用するデータ(特徴量 X)と予測の対象であるデータ(y)を分けています。
# 特徴量とターゲット変数を分ける
X = data_encoded.drop('y', axis=1)
y = data_encoded['y']
全てのデータを、トレーニングデータとテストデータに分割
モデルの学習に使ったデータと、モデルを評価するためのデータが同じだと、真の予測性能がわかりません。未知のデータに対してモデルがどれだけ正しく予測できるかを測るためにデータをトレーニングセットとテストセットに分割しています。ここでは、全データの70%をモデルの学習(トレーニング)に、30%をモデルの評価(テスト)に使用します。
引数に値を指定しない場合は、トレーニングデータ:テストデータ=0.75:0.25で分割されるようです。(scikit-learn train_test_split を参照)
また、random_stateの値を指定することで、ランダムにデータが分割されるようになります。0、または42がよく使われるようです。
※0を指定する→毎回同じような形でデータが分割される→毎回同じ結果を得られる、と言うことになります。
# データをトレーニングセットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
欠損値の処理(今回の予測では行っていない)
データに欠損がある場合は補完したり、欠損値を除外する処理が必要になります。(が今回は欠損値がなかったため説明は省略いたします。)
特徴量の標準化
標準化とは、平均が0、分散が1となるようにデータを変換することです。(参照)
特徴量同士は、多くの場合異なる単位になっていると思います。
今回のデータセットを少し取り上げても、年齢(才)、残高(€)、顧客への連絡回数(回)など複数あります。
このような状況下でそのまま単位を考慮せずに予測を行ってしまうと、単純に値の大きいものが予測結果に強い重みを与えてしまう形となり、モデルが正確に予測をできない可能性があるため、標準化を行います。式にするとこのような形です。
x \longmapsto \frac{x - \overline{x}}{s}
(x:値、\overline{x}:平均値、s:標準偏差)
ロジスティック回帰モデルの構築・学習
前処理が完了したところで、ロジスティック回帰モデルの構築に入ります。
sklearnというライブラリの、LogisticRegressionクラスを使うことで簡単にモデルが生成できます。
さらにfitメソッドを使い、引数にトレーニングデータを指定してあげれば学習を行うことができます。
# ロジスティック回帰モデルの構築と学習
model = LogisticRegression(max_iter=1000)
model.fit(X_train_scaled, y_train)
テストデータを使用し、予測を行う
同じくLogisticRegressionクラスのpredictメソッドを使うことで、テストデータに対する予測を行うことができます。
# テストデータで予測
y_pred = model.predict(X_test_scaled)
さらに、accuracy_scoreメソッドや
classification-reportメソッドを使うことでモデルの精度、評価を表示することができます。
accuracy,reportの出力結果はこんな感じでした。

表の各項目について
-
precision→適合率。モデルがクラス「1」(定期預金の申込みを行う)と予測したもののうち、実際に「1」であったものの割合のことを指します。(クラス0においても同様)
-
recall→再現率。実際に「1」であるもののうち、モデルがどれだけ「1」と正しく予測できたかの割合のことを指します。(クラス0においても同様)
-
f1-score→F1スコア
適合率と再現率の調和平均をとったものです。
※一般に適合率と再現率はトレードオフの関係にあります。 -
support→各クラスに属するサンプル数です。
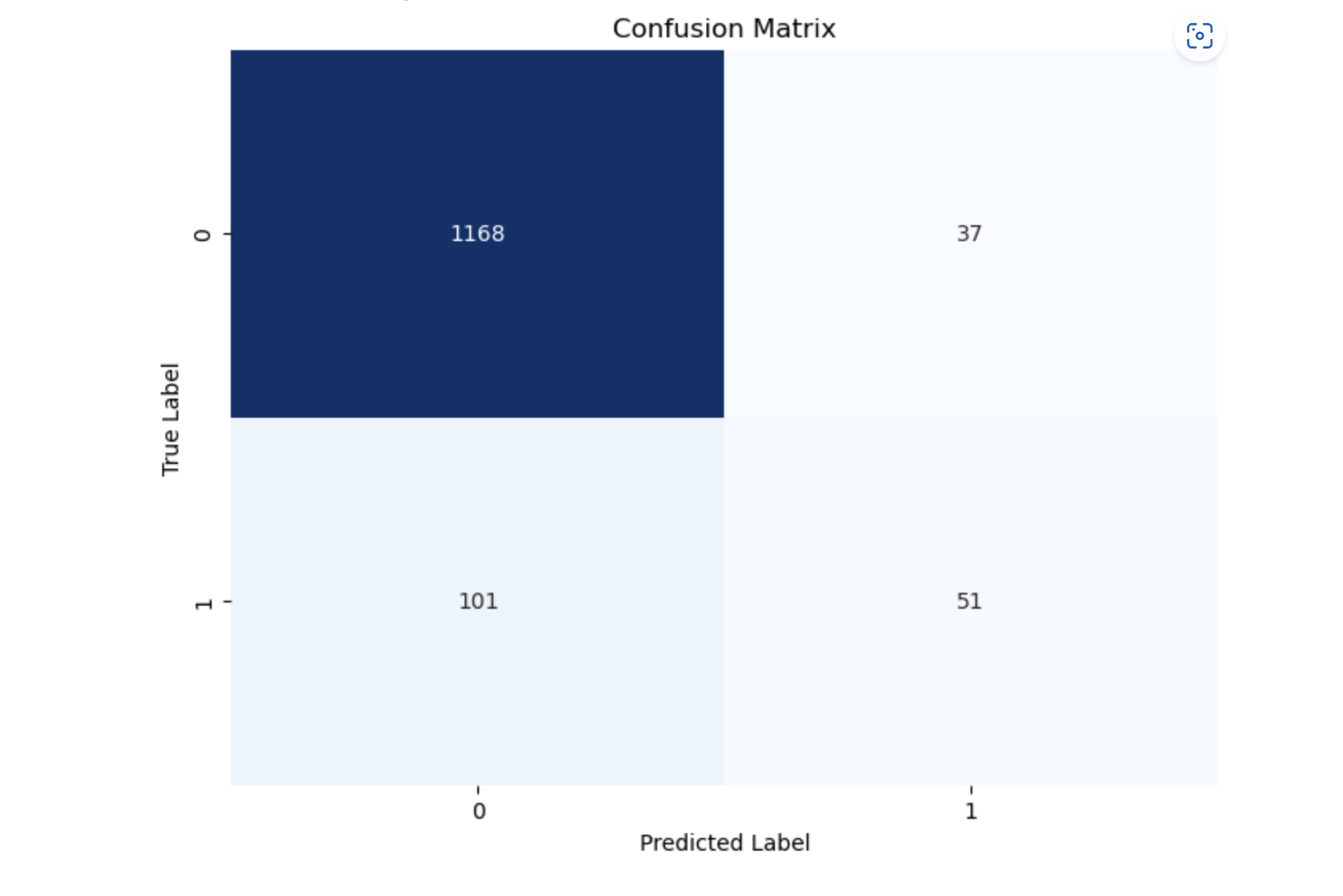
モデルの精度は89%と、良い結果が出ています。ただ、これは主にクラス「0」(加入しない)に偏った予測によるものです。
データの分布を見てみると、0(定期預金の申込みをしなかった)は1205個、1(定期預金の申込みを行った)は152個と、かなりの偏りがあります。クラス「1」(定期預金の申込みを行った)に対する予測は、適合率が低く、特に再現率が34%と低いため、改善が必要な結果となってしまいました。
アンダーサンプリングやオーバーサンプリングと呼ばれる手法を使い、この問題に対処する必要がありそうですが、今回の検証はここまでとします。
前処理〜予測の部分までのコードをまとめるとこんな感じです。
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, classification_report
# データの読み込み
data = pd.read_csv('bank.csv', sep=';')
# ターゲット変数を 'y' に設定し、数値化
data['y'] = data['y'].apply(lambda x: 1 if x == 'yes' else 0)
# カテゴリ変数をダミー変数に変換
data_encoded = pd.get_dummies(data, drop_first=True)
# 特徴量とターゲット変数を分ける
X = data_encoded.drop('y', axis=1)
y = data_encoded['y']
# データをトレーニングセットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 特徴量の標準化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
# ロジスティック回帰モデルの構築と学習
model = LogisticRegression(max_iter=1000)
model.fit(X_train_scaled, y_train)
# テストデータで予測
y_pred = model.predict(X_test_scaled)
# モデルの精度と評価を表示
accuracy = accuracy_score(y_test, y_pred)
report = classification_report(y_test, y_pred)
print(f'Accuracy: {accuracy}')
print(report)
予測結果の可視化
予測結果を、グラフに可視化してみます。今回は混同行列という、モデルの予測が正しいかどうかを表す行列を図示してみます。
Seaborn(sns)は、ヒートマップなどで可視化を行う際に使用するライブラリ、
Matplotlib(plt)はpythonでグラフの描画を行う際よく使用されるライブラリです。
さらにsklearnのconfusion_matrixメソッドは混同行列を計算するためのメソッドです。
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix, roc_curve, roc_auc_score
# 混同行列の作成と可視化
conf_matrix = confusion_matrix(y_test, y_pred)
plt.figure(figsize=(8, 6))
sns.heatmap(conf_matrix, annot=True, fmt='d', cmap='Blues', cbar=False)
plt.title('Confusion Matrix')
plt.xlabel('Predicted Label')
plt.ylabel('True Label')
plt.show()
結果はこのような形になりました。(表のラベル名を日本語にするとうまく表示できなかったため英語でラベル名を記載しています)
各ラベルが同じ値となっている部分が、正しく予測できている部分となります。
それぞれTP(True Positive:真陽性)、TN(True Negative:真陰性)と呼ばれます。
逆にラベルの値が一致しない部分は、FP(False Positive:偽陽性)、FN(False Negative:偽陰性)と呼ばれます。
先ほど出てきた再現率、適合率などは上記を使って求めることができます。(ここでは算出式は省略します)
特徴量の影響度を確認
ロジスティック回帰モデルで行われた予測において、どの特徴量がどの程度予測に大きく影響を与えるかを確認してみます。
# ロジスティック回帰モデルの係数を確認する
coefficients = model.coef_[0]
feature_names = X.columns
# 係数と特徴量名を対応させてデータフレームにまとめる
coef_df = pd.DataFrame({
'Feature': feature_names,
'Coefficient': coefficients
})
# 係数の絶対値が大きい順に並べ替える
coef_df_sorted = coef_df.sort_values(by='Coefficient', ascending=False)
# 結果を表示
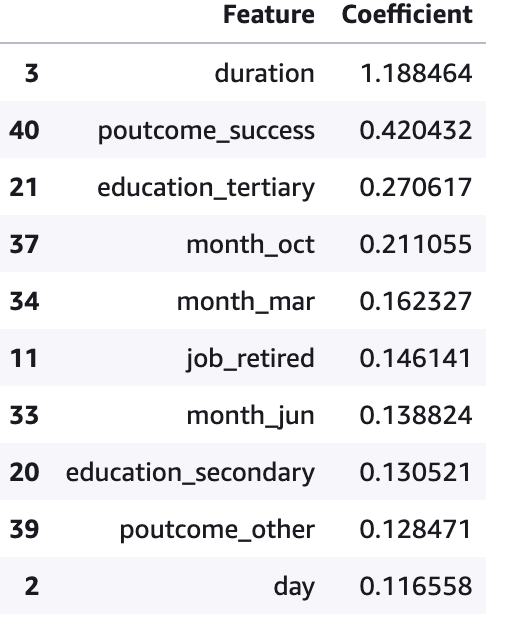
coef_df_sorted.head(10) # 重要な特徴量上位10件を表示
なお、
model.coff_[0]
の中身は以下のようになっており、学習後の各特徴量に対してどの程度の重みを与えているかを表す値が格納されています。
[ 0.00273392 -0.07242202 0.11655788 1.18846401 -0.22951515 -0.03512759
-0.00441958 -0.1718337 -0.20935035 -0.01476233 -0.03074938 0.14614142
-0.02976859 -0.09503449 0.07606954 -0.06812567 -0.15655983 0.01561623
-0.19012364 -0.10977665 0.1305215 0.2706174 -0.09693977 0.10613093
-0.11875259 -0.1927614 -0.03181743 -0.60414622 -0.21476679 0.00141984
-0.00294772 -0.18637613 -0.28827953 0.13882395 0.16232703 -0.36836235
-0.22633907 0.21105531 0.05555708 0.12847149 0.42043219 -0.02609539]
結果は以下のようになりました。
duration(連絡時間)、poutcome_success(過去のマーケティングキャンペーンの結果が成功している)、education_tertiary(高等教育を受けている)、が係数の上位に来ています。私の直感的には、job_retired(仕事を退職した人)が、金銭面に余裕ができる傾向にあるからこそ、係数の上位に来るかと思いましたが、意外にも6番目でした。
まとめ
今回はロジスティック回帰を使って、予測を行うモデルを構築しました。
机上で問題集などを解くだけの学習より、実際に手を動かしながら学習することで少しは理解の助けになった気がします。また、今回機械学習を使うことで、自分の直感と、客観的な分析のズレに気づける面白さを実感しました。
そして、今回使用したデータセットはどうやらデータ分析コンペであるKaggleの問題にも使用されているようで、Kaggleにも興味が湧いてきました。習うより慣れろの精神で、一度チャレンジしてみたいなとも思います。