はじめに
この記事は、銀河の平和と秩序を維持する共和騎士たちが、とある惑星系シミュレーターを一晩で完成させるために奔走する物語です。
プログラミングの基礎知識さえあれば、実際に手を動かしながらこの記事を読み進めることで 誰でも簡単に次のような CG プログラムを作ることができる ようになるでしょう。

Gopher君がゆく シリーズ
この記事は「Gopher君がゆく Episode I」の続編となります。
ストーリーを重視される方は、先に Episode I から読むことをおすすめしますが、取り扱う技術テーマに関連性がないため、この記事から読んでいただいても理解の妨げになることはありません。
なお、Gopher君の身体能力に興味がある方は、本編へ進む前に Episode I にエンベデッドした 5 つの GIF animation を見ておきましょう。
登場人物
| 呼称 | 居住地 | 概要 |
|---|---|---|
| パダワン (ミジンコ) |
惑星タトゥイーン | 類まれな才能と驚異的なミディ=クロリアン値を持つ。 イニシエイトを卒業したばかりで、未だ修行中の身。 |
| マスター | 惑星タトゥイーン | 評議会の意向を無視するなど、型破りな騎士。 高い実力と指導力を持つ。 |
| Gopher君 | 不定 | 銀河各所に派遣されるエージェント。 驚異的な身体能力とバランス感覚とを合わせ持つ。 |
| 若きナイト | 惑星コルサント | 正義に燃える熱血漢。 パダワンからナイトへ昇格して数年経つ。 |
| グランドマスター | 惑星コルサント | 共和騎士 最高評議会を統率する長老。 |
| 最高議長 | 惑星コルサント | 銀河共和国 元老院の最高議長。 |
前提条件
- 本稿では Processing 3.5.4 を使って開発を進めます。
このため Java のコーディング経験があると良いでしょう。 - また、プログラム内で以下の計算を行いますが、高度な数学の知識は必要ありません。
- 惑星と衛星の軌道を計算するために簡単な三角関数を使います。
- 座標変換のために簡単な行列演算を使います。
開発および動作環境
本編に記載したプログラムは、以下の環境でのみ動作を確認していますが、Processing はマルチプラットフォームに対応しています。もし Linux や Mac OS などで動作確認できた場合は、是非、教えてもらえると嬉しいです。
- HW: Thinkpad X1 Extreme
(NVIDIA GeForce GTX 1050 ti with Max-Q Design) - OS: Windows 10 x64 Version 1903
開発ツール
| カテゴリ | ツール | 用途 |
|---|---|---|
| 言語および IDE | Processing 3.5.4 | Java 系言語による 3DCG のプログラミング |
| グラフィック編集 | Gimp 2.10.10 | 画像素材の作成や背景加工 |
どちらも無償ツールです。
免責事項
- タイトルで「太陽系シミュレーター」を謳っていますが、本稿は、ニュートン力学などによる物理モデル(たとえば重力相互作用する N 体シミュレーションなど)を扱うものではありません。
- 本稿で扱う惑星および衛星の軌道は楕円軌道ではありません。公転体は、母星を中心とする同一平面上の円軌道を等速で動くものとしています。
- 天体の直径、公転半径、公転周期は現実の値を元にデフォルメしています。
- 最終的なプログラムで扱うオブジェクト(恒星、惑星、衛星など)は、平面にテクスチャーをマッピングしたビルボードであり、3D モデルではありません。
- Gohper君が登場するにもかかわらず、Golang の話題は出てきません。
- 本編中で使われている以下の用語は物語の性質上必要となるものですが、2020年8月現在、日本国内で一般的に認知されている表現ではありません。
- プログラム (program)、および、プログラミング言語 (programming language) のことを「セーバー」と呼ぶことがあります。
- また同様に、プログラマ (programmer) のことを「セーバー使い」と呼ぶことがあります。
- 数直線上の負の無限大方向を「ダークサイド」または「暗黒面」と呼ぶことがあります。
- また同様に、数直線上の正の無限大方向を「ライトサイド」と呼ぶことがあります。
- 本文中にエンベデッドされた映像 (GIF animation) には音声が含まれておりません。臨場感が不足していると感じられる場合は、ご自身で音源をご用意いただいた上で再生してください。5.1ch または 7.1ch の音源と再生装置をご利用いただくことにより、より臨場感を味わうことができるでしょう。なお、適切な音源がご用意できない場合は、こちら よりお選びいただくこともできます。
本編
A long time ago in a galaxy far, far away....
(遠い昔、はるか彼方の銀河系で …)
銀河元老院は混乱に渦巻いていた。
ドロイド軍率いる独立星系連合に対抗するために軍を創設すべきかどうかで議会が紛糾していたのだ。
その裏で共和騎士 評議会は、マスターとパダワンを極秘裏に 惑星タトゥイーン から呼び寄せていた。
午後 8 時|プロローグ
惑星コルサント 共和騎士 評議会室にて …
グランド・マスター「遠いところご苦労じゃった」
マスター「いえ、とんでもない。パダワンなんて久しぶりの大都会に大はしゃぎですよ」
マスター「ところで …」
グランド・マスター「その話じゃが、、」
グランド・マスター「実は、今、元老院で紛糾している議案が通った場合に備えて、、」
グランド・マスター「密かにクローン軍の製造と訓練ができる星を探しているのじゃが、」
グランド・マスター「至急、その候補となる星系のシミュレーションをしてほしいのじゃ」
マスター「なるほど。で、どの星系ですか?」
グランド・マスター「天の川銀河にある『太陽系』という星系じゃ」
マスター「そんな辺境の?」
グランド・マスター「ああ、あそこなら独立星系連合の手も回るまい」
惑星コルサント・共和騎士テンプルにて …
若きナイト「やあ、ミジンコ君」
若きナイト「太陽系のシミュレータを作るんだって?」
パダワン(ムカッ …)
パダワン「うん。さっきマスターから聞いた」
パダワン「てか、なんで僕のことミジンコって言うのさ!?」
若きナイト「がはは。それは君がまだミジンコみたいに小っちゃいからだよ」
若きナイト「はたしてミジンコ君にシミュレータなんて作れるのかなあ???」
パダワン(こいつ、まじムカつく!!!)
若きナイト「おお、君の師匠が来たようだよ」
若きナイト「それじゃ僕はそろそろ行くね!」
若きナイト「せいぜい頑張ってね」
若きナイト(あの小僧、やはり感情を上手くコントロールできないようだ)
若きナイト(ミディ=クロリアン値が異様に高いだけに、逆に危険な臭いがするぜ)
マスター「おお!パダワンよ」
マスター「ここに居たのか!」
マスター「どうかしたのか?」
パダワン「…」
パダワン「ねぇ、僕、ミジンコなの?」
マスター「そう言われたのか?」
マスター「がはは!お前は背が低いからな」
パダワン「…」
マスター「いいか、ミジンコっていうのはな、」
マスター「自分の体長の 20 倍以上もジャンプできるんだ!」
マスター「そんな騎士は銀河中探したっていやしない」
パダワン「すげ!」
パダワン「Gopher君よりすげ!」
パダワン「ミジンコ最高!」
パダワン「僕にもシミュレータ作れるかなあ?」
マスター「もちろんだ!」
マスター「今回は修行の一環として、お前主体で作れという指示を受けている」
パダワン「ねぇ、太陽系ってどんなとこ?」
パダワン「すげーど田舎なんでしょ!?」
マスター「第 3 惑星の地球という岩石惑星があって、」
マスター「その衛星の『月』という星がとてつもなく大きいんだ」
マスター「今回のシミュレーションの主な目的は」
マスター「月の重力が地球へどの程度影響を与えているかを知ることなんだ」
パダワン「へ~、どんな種族が住んでんだろ???」
マスター「地殻変動が活発でメタンや二酸化炭素量も多いようだが」
マスター「生命体がいるらしいという情報もある」
マスター「これが共和騎士 図書館で得られた」
マスター「唯一の地球人の映像だ」
パダワン「げっ!」
パダワン「地球人かっけー!」

(出典: Pixabay)
午後 9 時|Processing の導入、3DCG 入門
マスター「それでは早速始めよう!」
マスター「本来なら、C++ などで OpenGL を使いたいところだが、」
マスター「今回はアート用のセーバー、 Processing を使おうと思う」
マスター「Java ベースの環境だから、ほぼ Java と言っていいだろう」
パダワン「げっ! Java かよ。あのセーバーお堅い感じで、」
パダワン「イニシエイト時代に赤点だったんだよなぁ …」
パダワン「やな思い出 …」
マスター「Java ベースと言っても、」
マスター「グラフィックのために必要な変数やメソッドが既に準備されていて」
マスター「クラスを意識しなくてもいきなりセーバを使い始めることができるんだ」
マスター「OpenGL だと、本来集中したい 3DCG の殺陣(コーディング)に入る前に」
マスター「いろいろ面倒な儀式を行わなければならないが、」
マスター「その点、Processing はお前向きと言えるだろう」
21 時 05 分|Processing のダウンロードおよびインストール
マスター「Processing の IDE はここからダウンロードできる」
マスター「ダウンロードしたらインストール!と言いたいところだが、」
マスター「インストーラは付いていない」
マスター「zip を解凍したら適当なディレクトリに放り込んでおくだけだ」
21 時 10 分|Processing の起動
マスター「解凍したディレクトリにある processing.exe をダブルクリックするんだ」
パダワン「お、ダブルクリック、超得意!!!」
マスター「銀河標準ベーシック(脚注:日本語のこと)で何か入力してみなさい」
パダワン「げっ、文字化け!!!」
21 時 20 分|空間を知覚せよ
マスター「いいか、3DCG で大切なのは、三角関数でも行列演算でもない!」
マスター「最も大切なのは空間認識能力だ!(きっぱり)」
マスター「3DCG の世界は、宇宙空間と同じだ」
マスター「一度、飛び込んでしまったら、上も下もなく、」
マスター「相手が動いているのか、自分が動いているのかまるでわからなくなる。。」
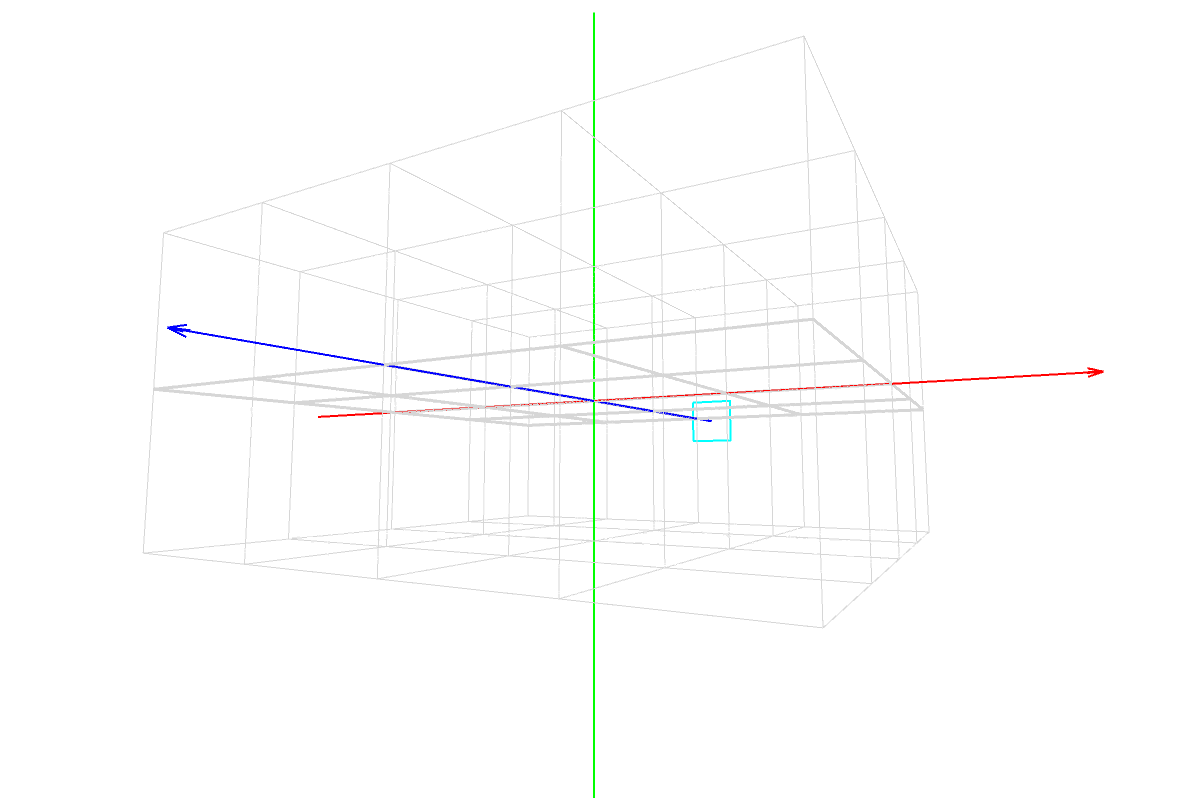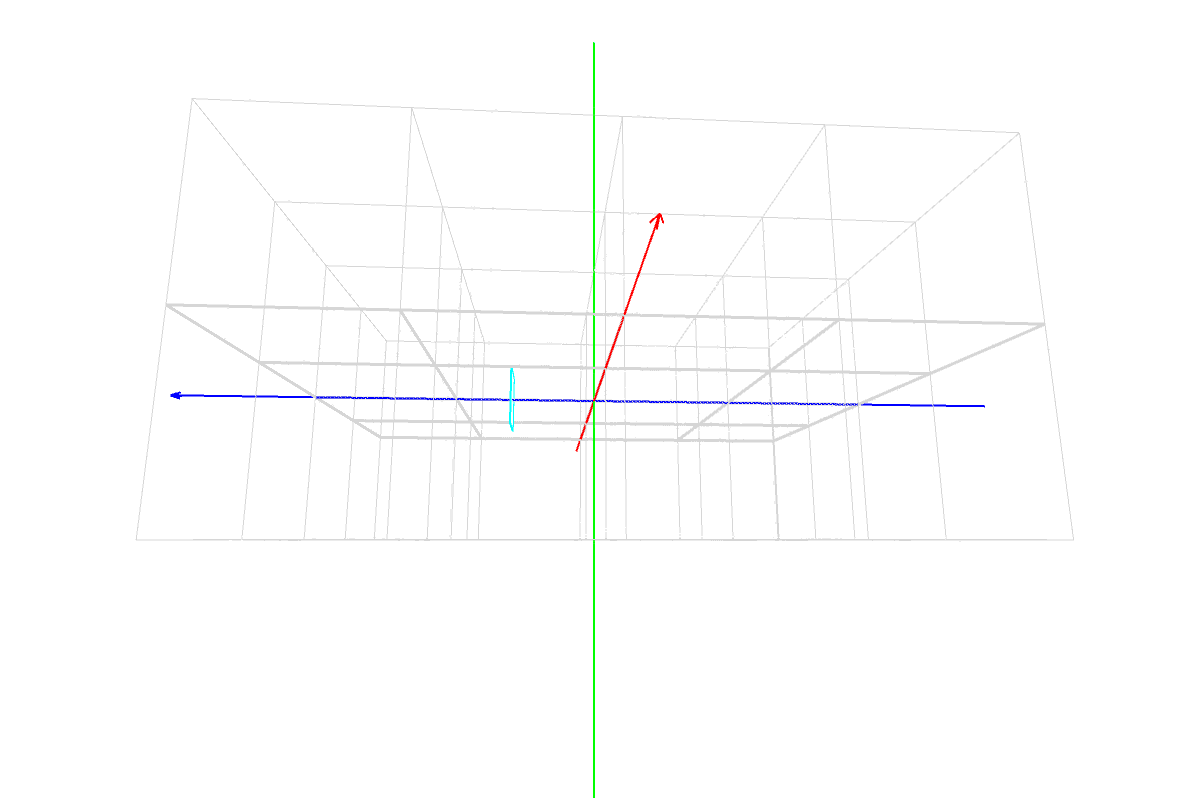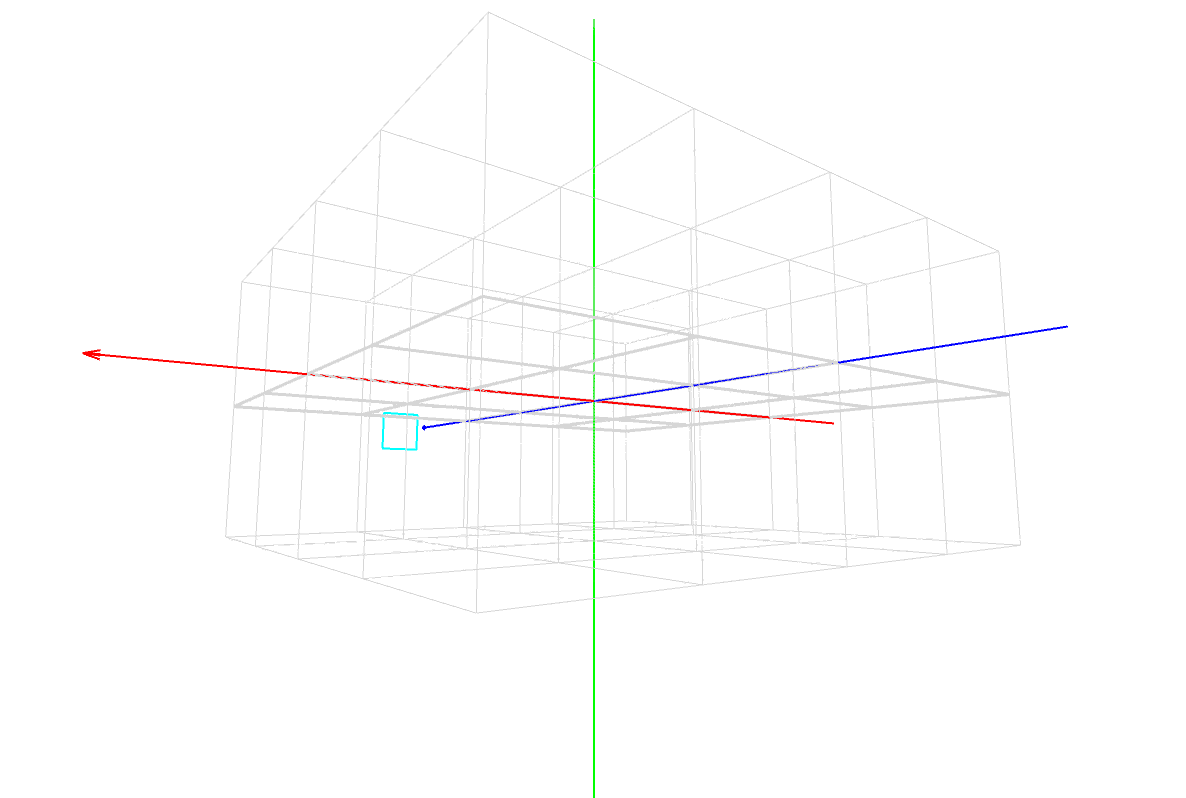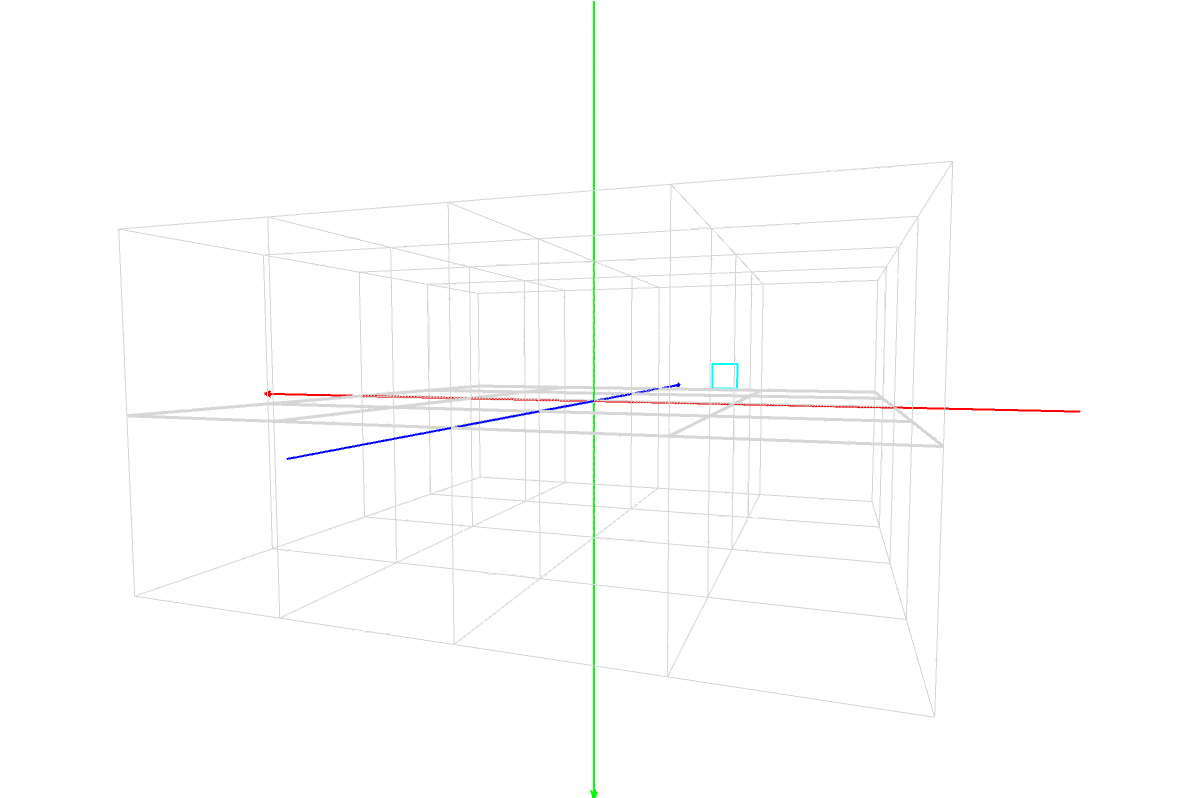
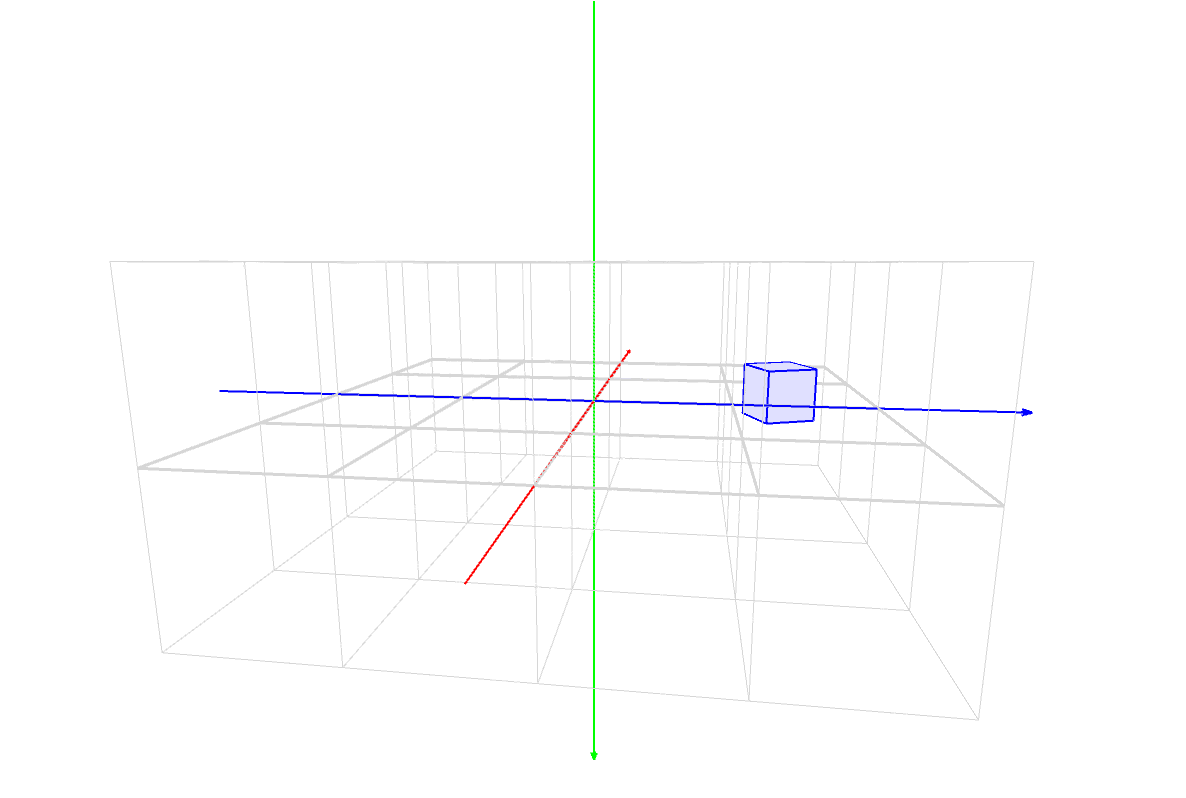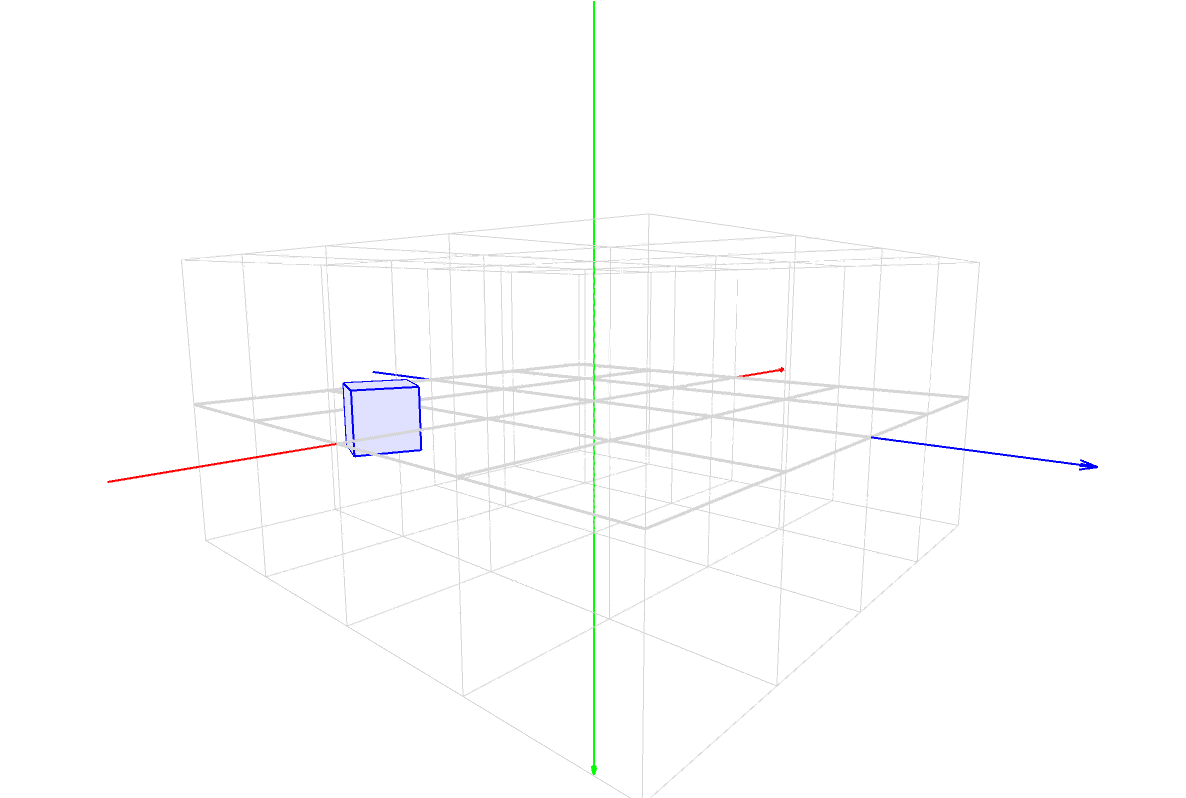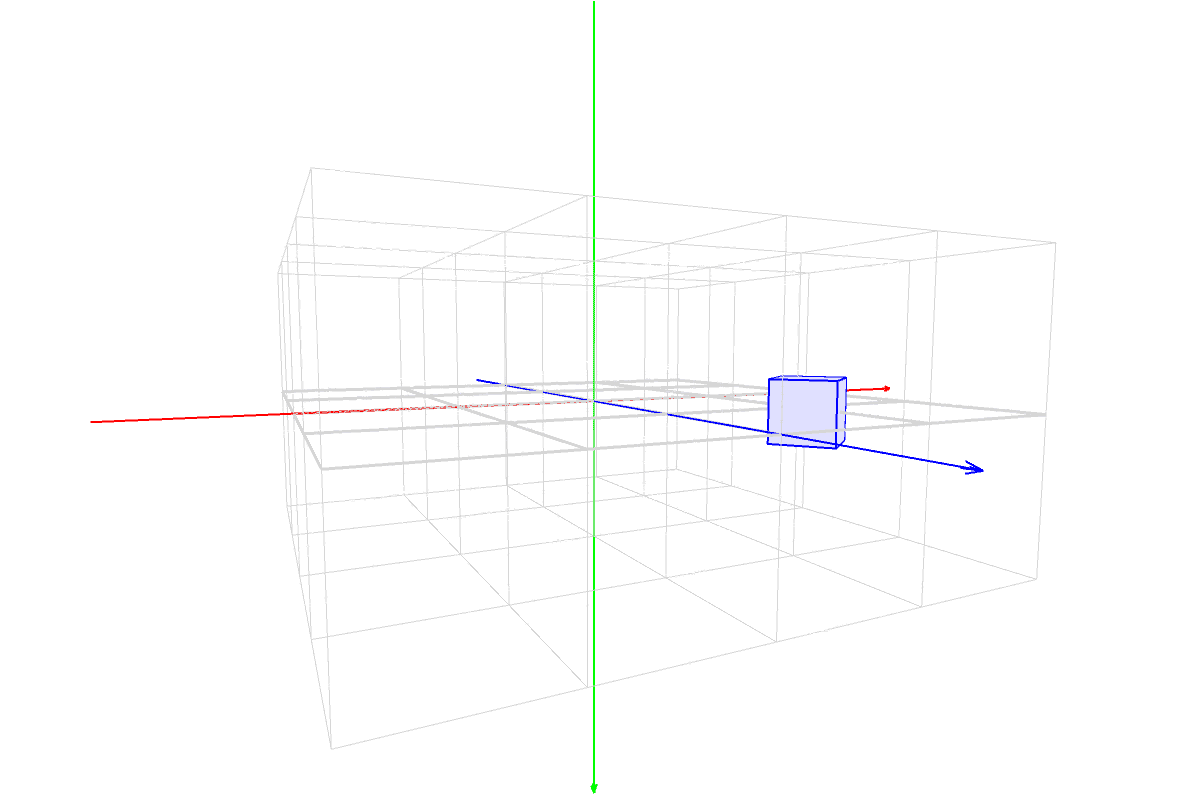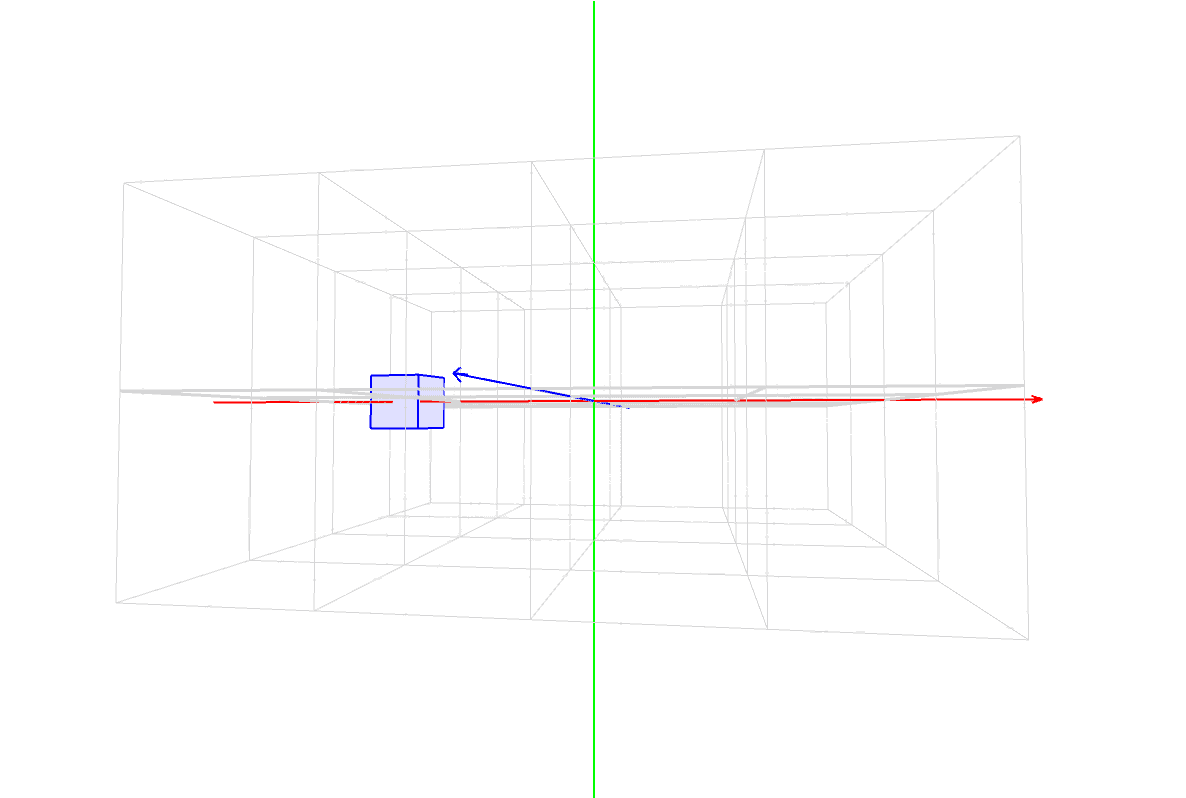
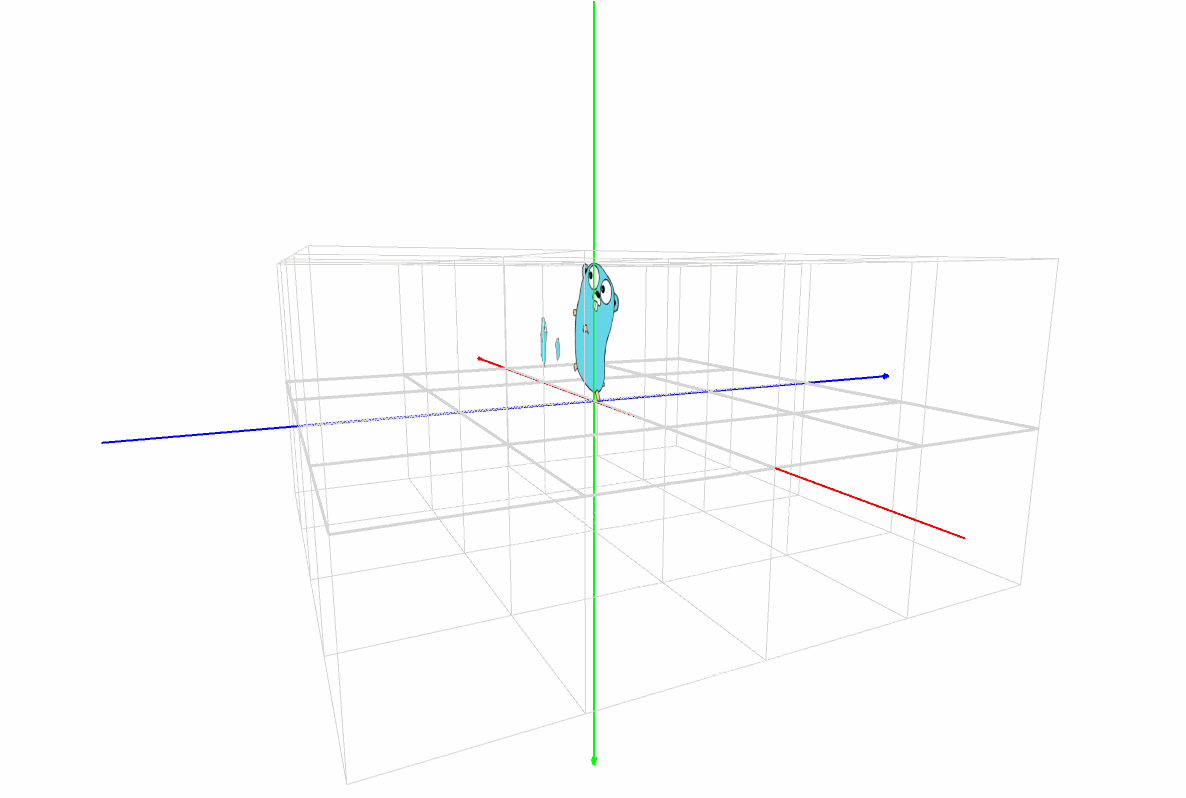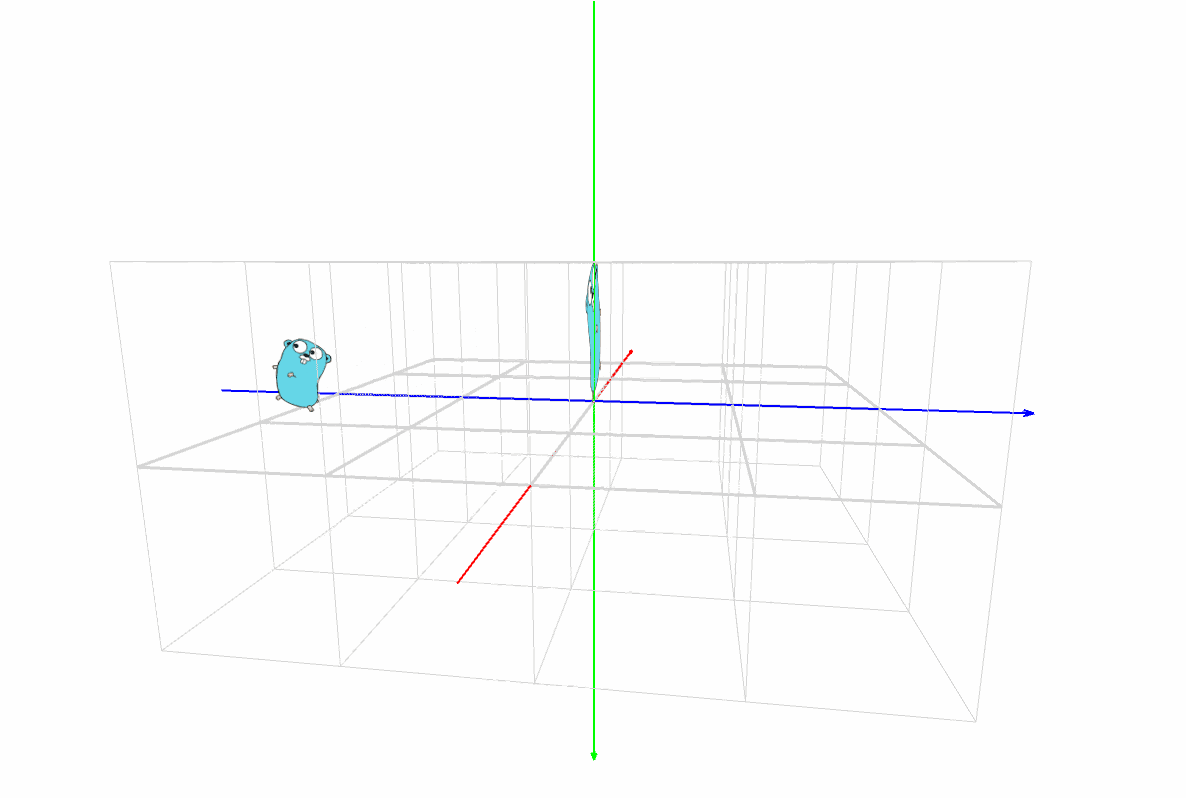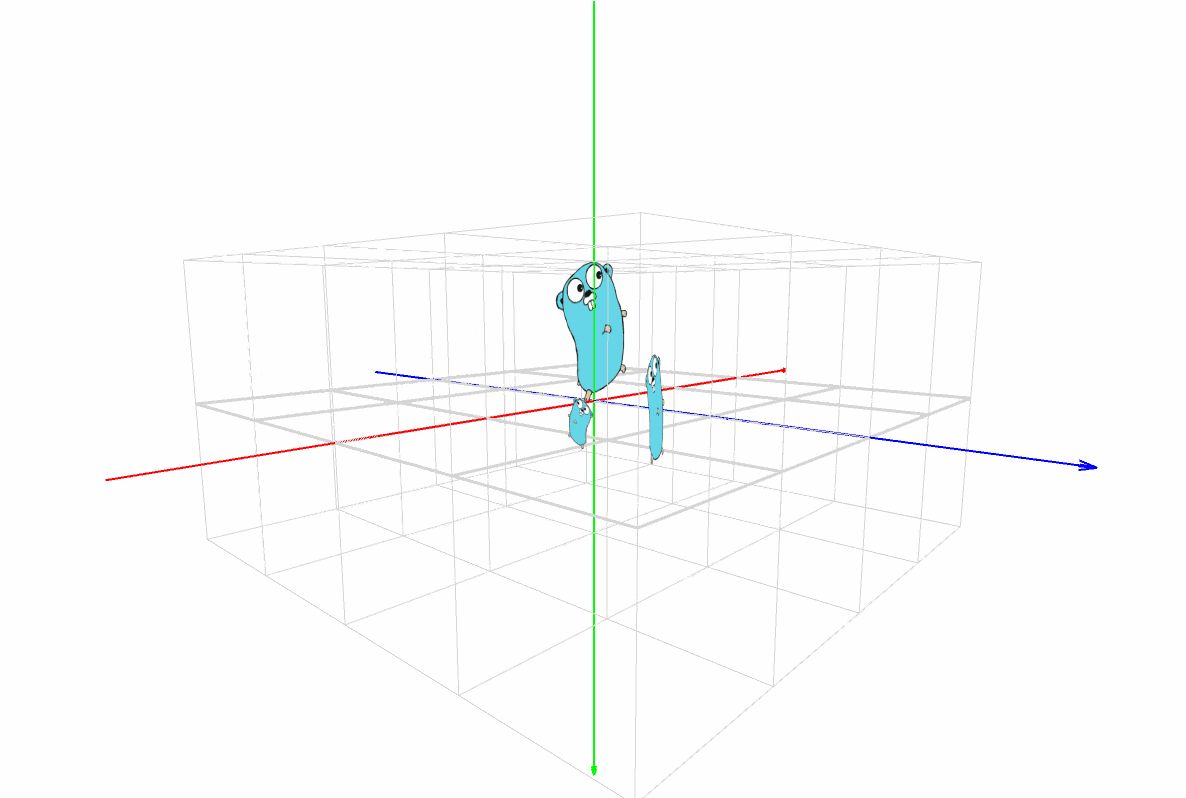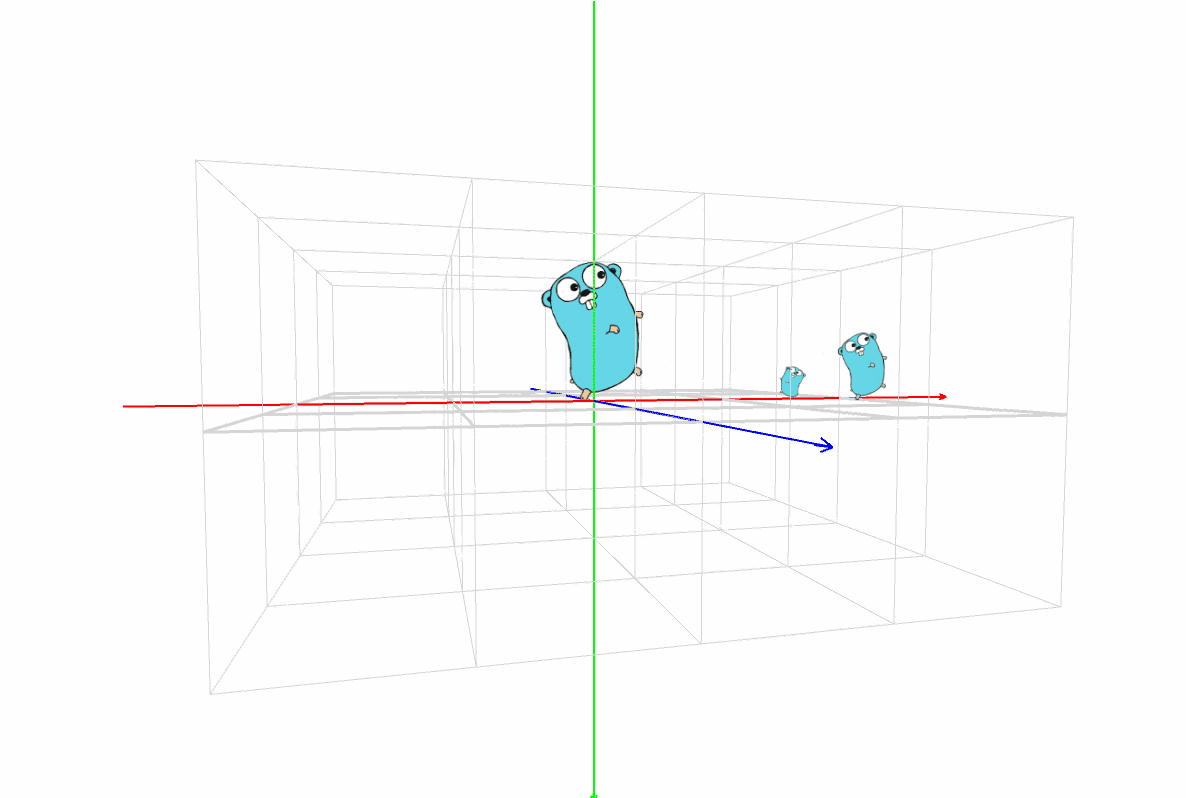
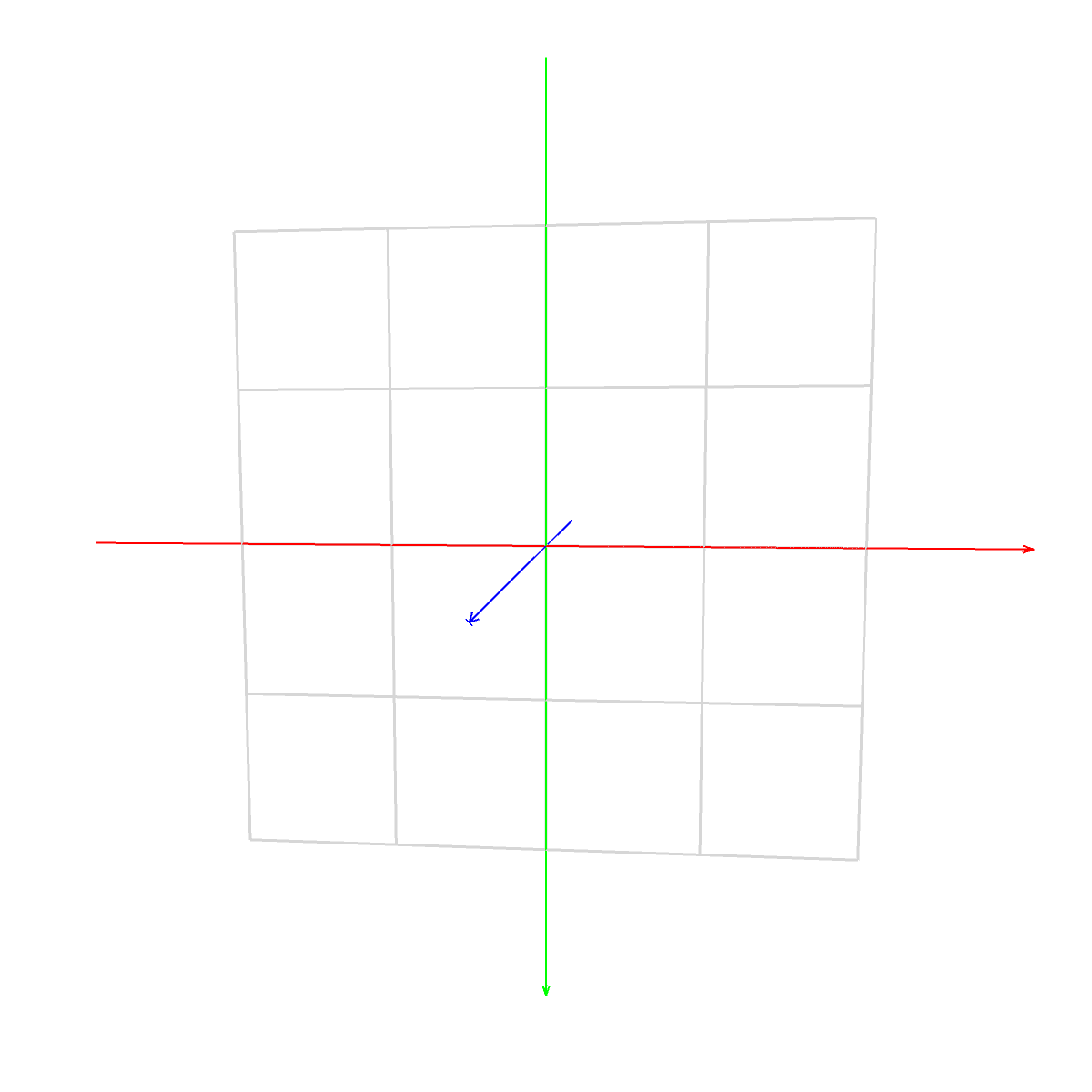
マスター「これは Processing のワールド座標系の座標空間だ」
マスター「赤がX軸、緑がY軸、青がZ軸」
マスター「まずはこのイメージを徹底的に頭に叩き込むんだ」
マスター「この図をイメージしながら左手の形をこうしてみろ!」
パダワン「あ、フレミングの法則!」
マスター「そうだ。あれと同じ形だ」
マスター「親指と人差し指と中指の3本を90度交差させるようにして、」
マスター「親指がX軸、人差し指がY軸、中指がZ軸、」
マスター「それぞれの指が指す方向がライトサイド(正の無限大の方向)だ」
マスター「その形を壊さないようにして、親指を右へ、人差し指を下に向けるんだ」
マスター「そうすると、中指はどこを向く?」
パダワン「えーと、自分の方を向いてる!」
マスター「そうだ。これが Processing の座標系で、『左手系』という」
パダワン「それなら、『右手系』もあるの?」
マスター「ある。右手系はZ軸の向きが左手系と逆なのだ」
マスター「また、Processing の座標系は、Y軸が下向きだから注意しろ!」
マスター「親指を右に向けたまま、人差し指を上に向けて見ろ」
パダワン「あ、中指がマスターを指してる …」
マスター「そうだ。同じ左手系でも、Y軸が上を向いているライブラリなどでは」
マスター「Z軸の向きが逆になるから注意しなさい」
マスター「もう一度、各軸の色と方向をイメージしろ!」
パダワン「赤のX軸が右向き …」
パダワン「緑のY軸が下向き …」
パダワン「青のZ軸がこっち向き …」
マスター「そうだ。体に染み込ませるんだ」
マスター「また、3 つの座標平面についても頭に入れておこう」
マスター「まずは XY 平面。これは目の前に立ちはだかる高い壁だ」
マスター「イニシエイト時代に 2 次元の座標系で」
マスター「何度もお目にかかっただろう」
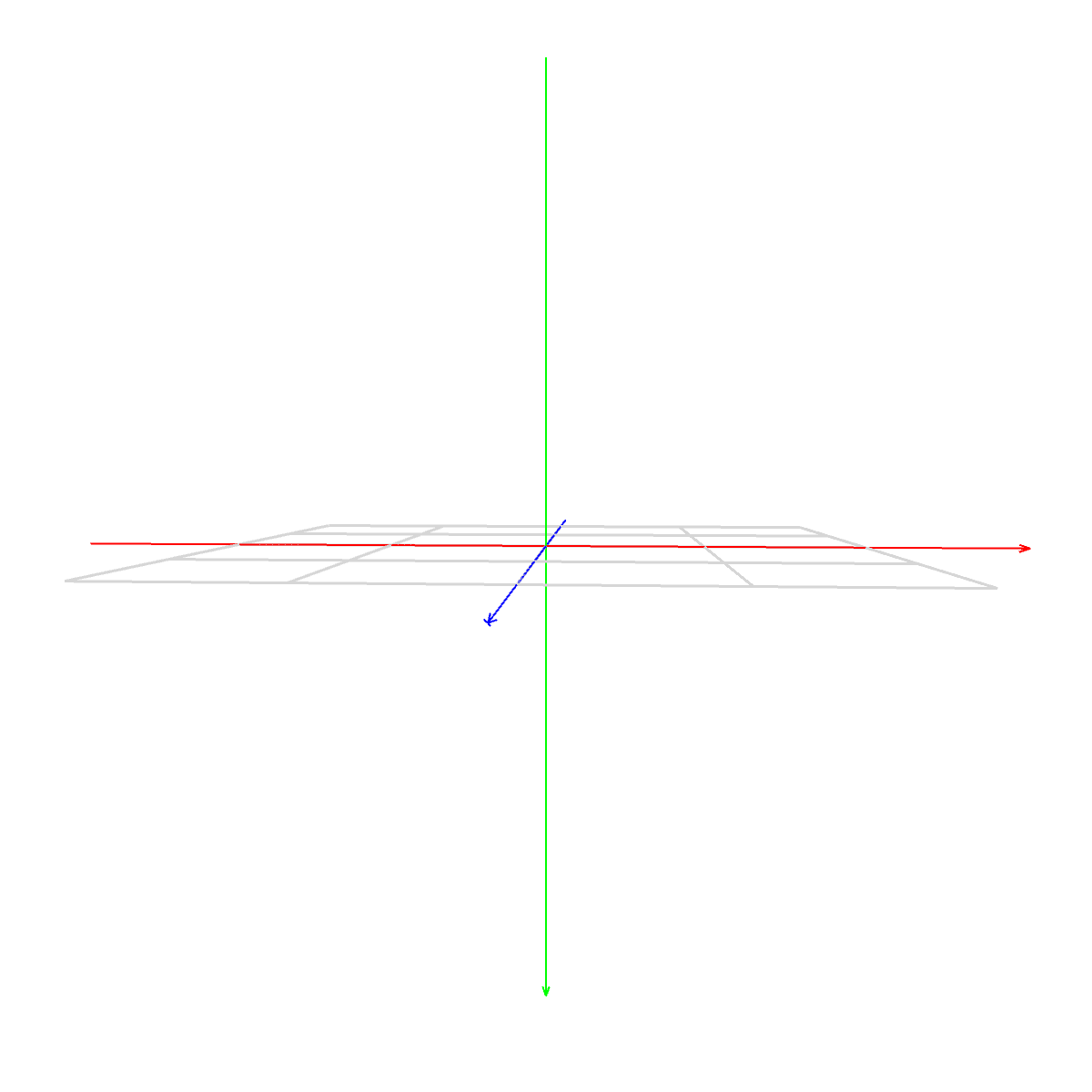
マスター「次に ZX 平面で、これは床だ」
マスター「今日の作業でも、この平面はたくさん出てくるはずだ」
マスター「しっかり覚えておくんだ」
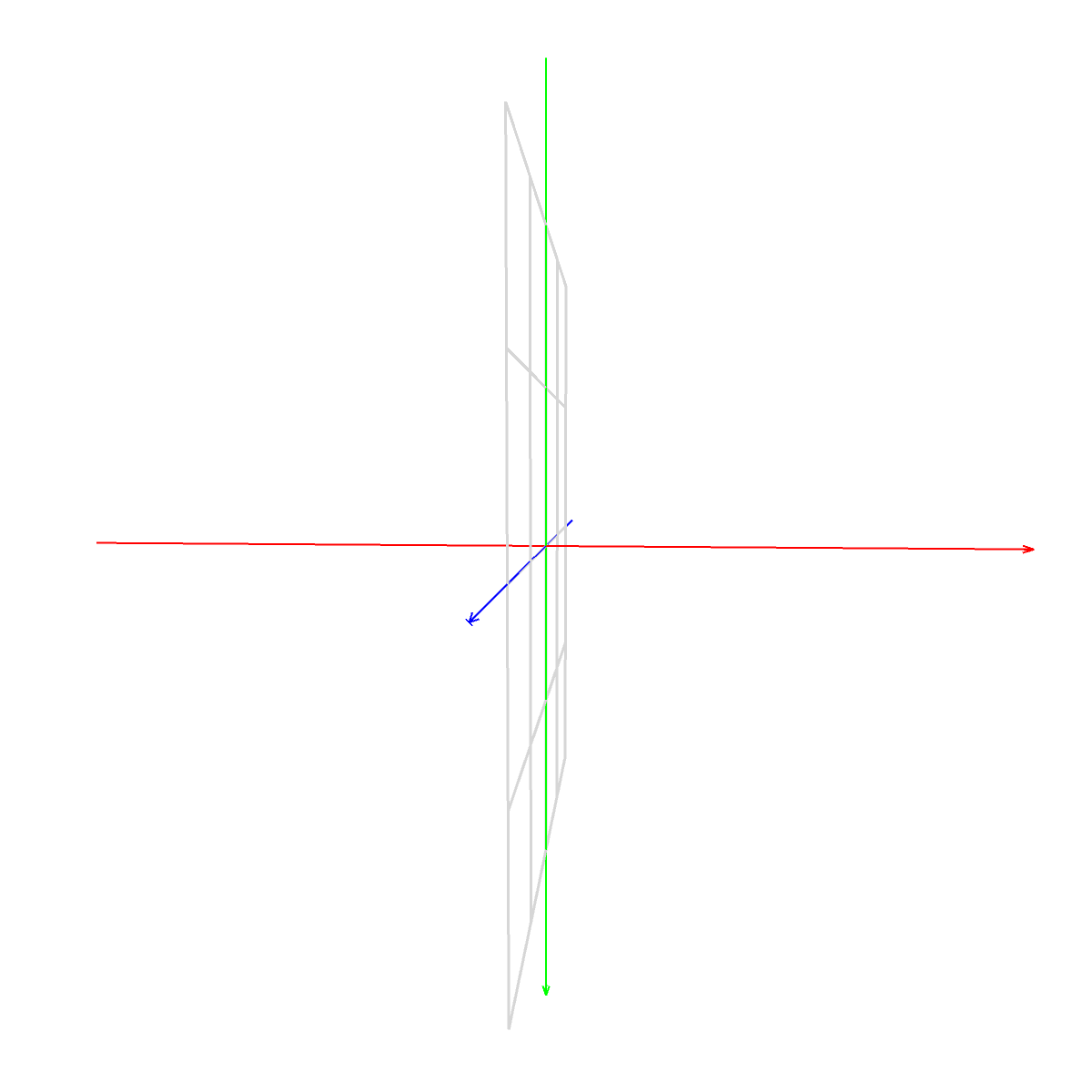
マスター「最後に YZ 平面だ」
マスター「これは『ごめん!』と誤ったときの」
マスター「手のひらの形だな」
21 時 30 分|新規スケッチの作成
マスター「Processing ではプロジェクトのことを『スケッチ』というんだ」
パダワン「お絵かき!」
マスター「そうだ。Processing を立ち上げると」
マスター「自動的に新規スケッチが作成されるから」
マスター「既に開いているスケッチに名前を付けて保存する」
マスター「保存する場所を選んで、ひとまず "Learning" という名前で保存だ」
パダワン「お!、Learning ってフォルダができて、」
パダワン「その中に Learning.pde ができてる」
マスター「そうだ。それが Processing の」
マスター「スケッチフォルダーとスケッチファイルだ」
マスター「これから、ここに少しづつ書き足していくから」
マスター「こまめに Ctrl+S で保存するのを忘れないようにな」
21 時 40 分|最初のコーディング
マスター「それではいよいよ殺陣に入る」
マスター「IDE に次のように入力するんだ!」
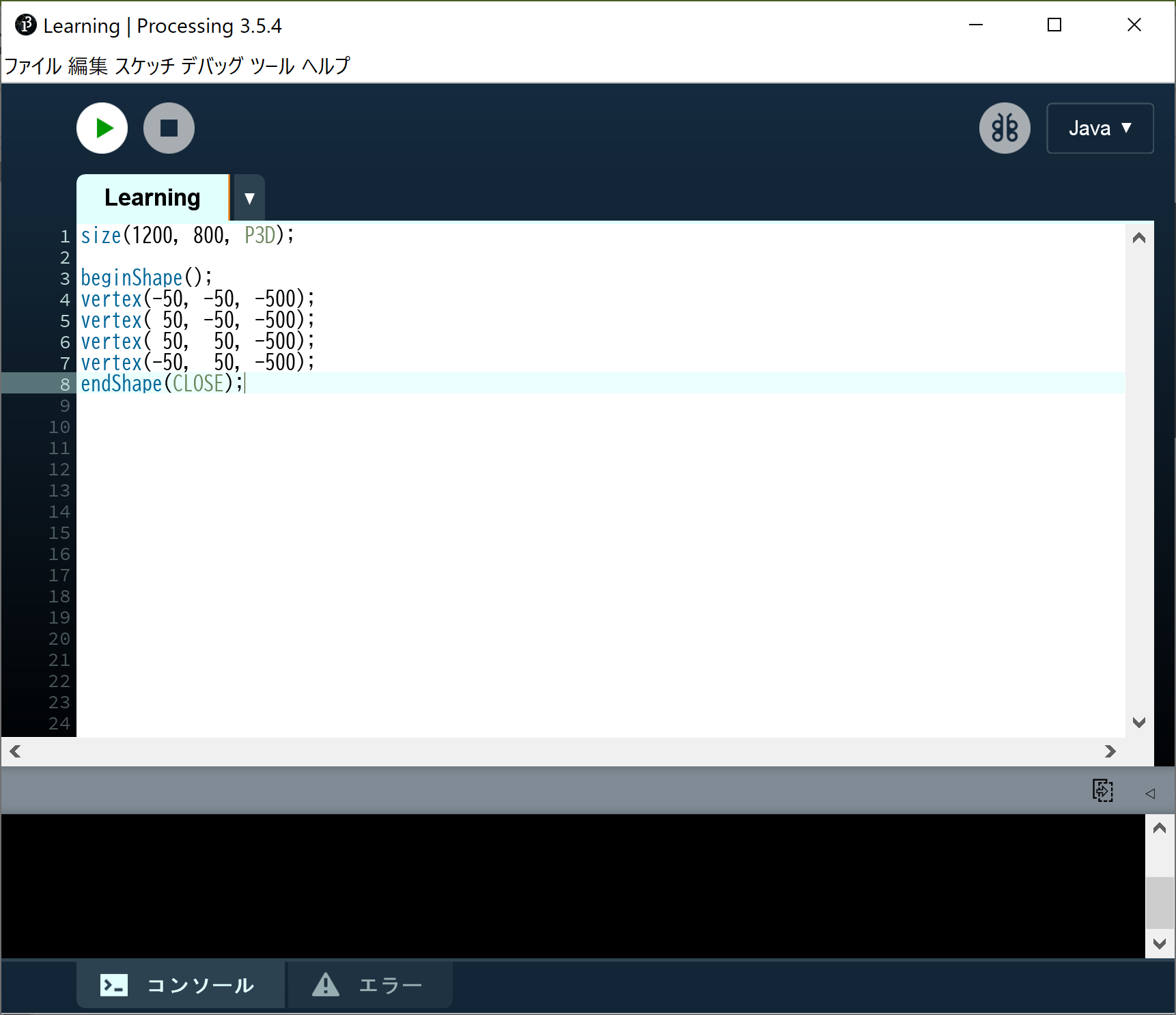
パダワン「げ、クラス定義も main メソッドもいらねーの?!」
パダワン「ラクすぎてウケる(笑)」
size(1200, 800, P3D);
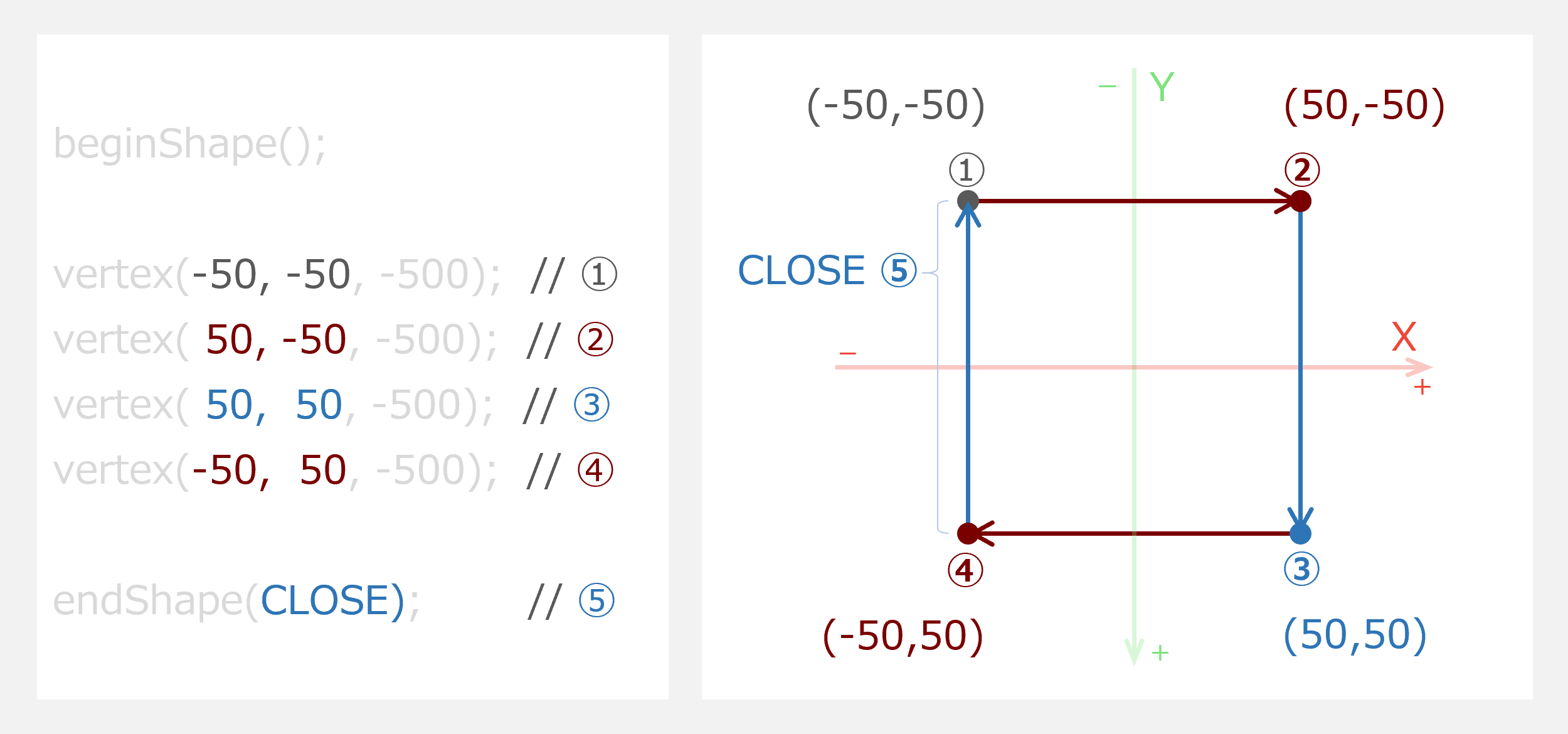
beginShape();
vertex(-50, -50, -500);
vertex( 50, -50, -500);
vertex( 50, 50, -500);
vertex(-50, 50, -500);
endShape(CLOSE);
マスター「この意味を説明する」
-
size(1200, 800, P3D);
これはウインドウサイズの指定だ。1200が幅で、800が高さ。
今回は 3DCG だから3つ目のパラメータはP3Dと指定する。 -
beginShape();
これから図形を描画するということを Processing に伝える宣言だ。 -
vertex(...); x 4行
vertex は頂点をいくつか指定して、その頂点同士を結ぶ多角形を描画するメソッドだ。ここでは 4 つの vertex で頂点を指定しているから、四角形を描画することになる。 -
endShape();
図形が書き終わりましたという宣言だ。パラメータに渡している CLOSE は図形を閉じるという意味だ。これを指定しないと最初の頂点と最後の頂点が結ばれない開いた図形になってしまう。
マスター「いいか、ワールド座標系のイメージが難しければ、」
マスター「まずは XY 平面だけ考えるんだ」
マスター「XY 平面のイメージができたら、次は Z 座標だ」
マスター「どの頂点も Z 座標は -500 だ」
マスター「原点(0,0,0)から見ると、ワールド座標系で -500 はどっちだ?」
パダワン「えーと、左手の親指が X、人差し指が Y …」
パダワン「親指 X を右に向けて、人差し指 Y を下に向けると …」
パダワン「中指 Z は、遠くからこっちに向かって数字がおっきくなるから …」
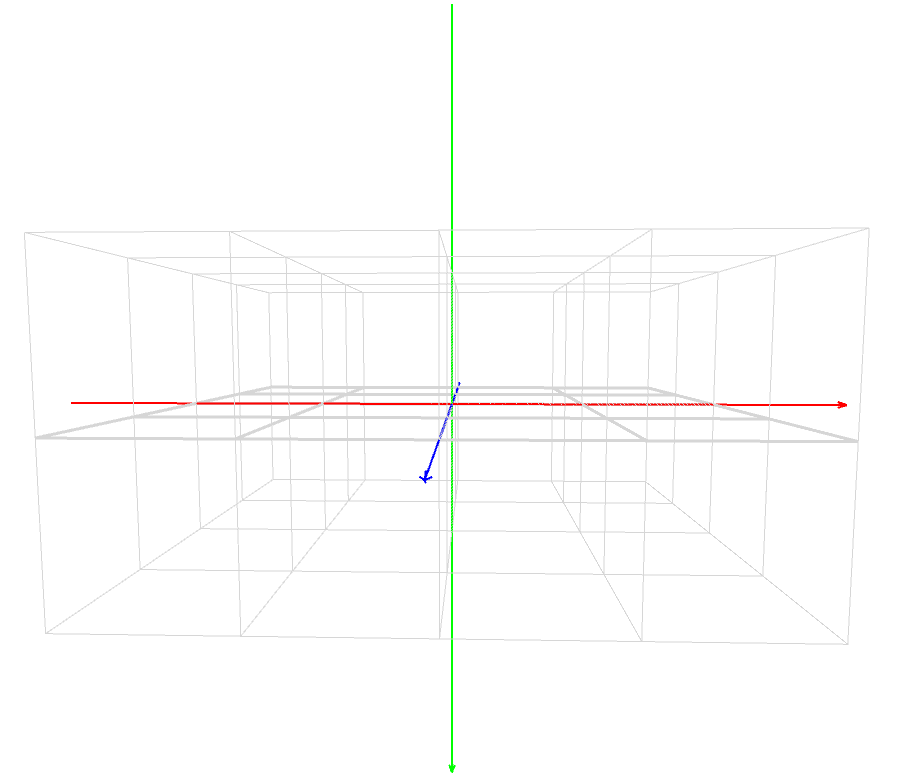
パダワン「-500 は、正面のずっと奥の方だあ!」
マスター「そうしたら、それが正しいかどうか確かめてみよう」
マスター「実行ボタン (タブのすぐ上の再生マークアイコン) をクリックするんだ」
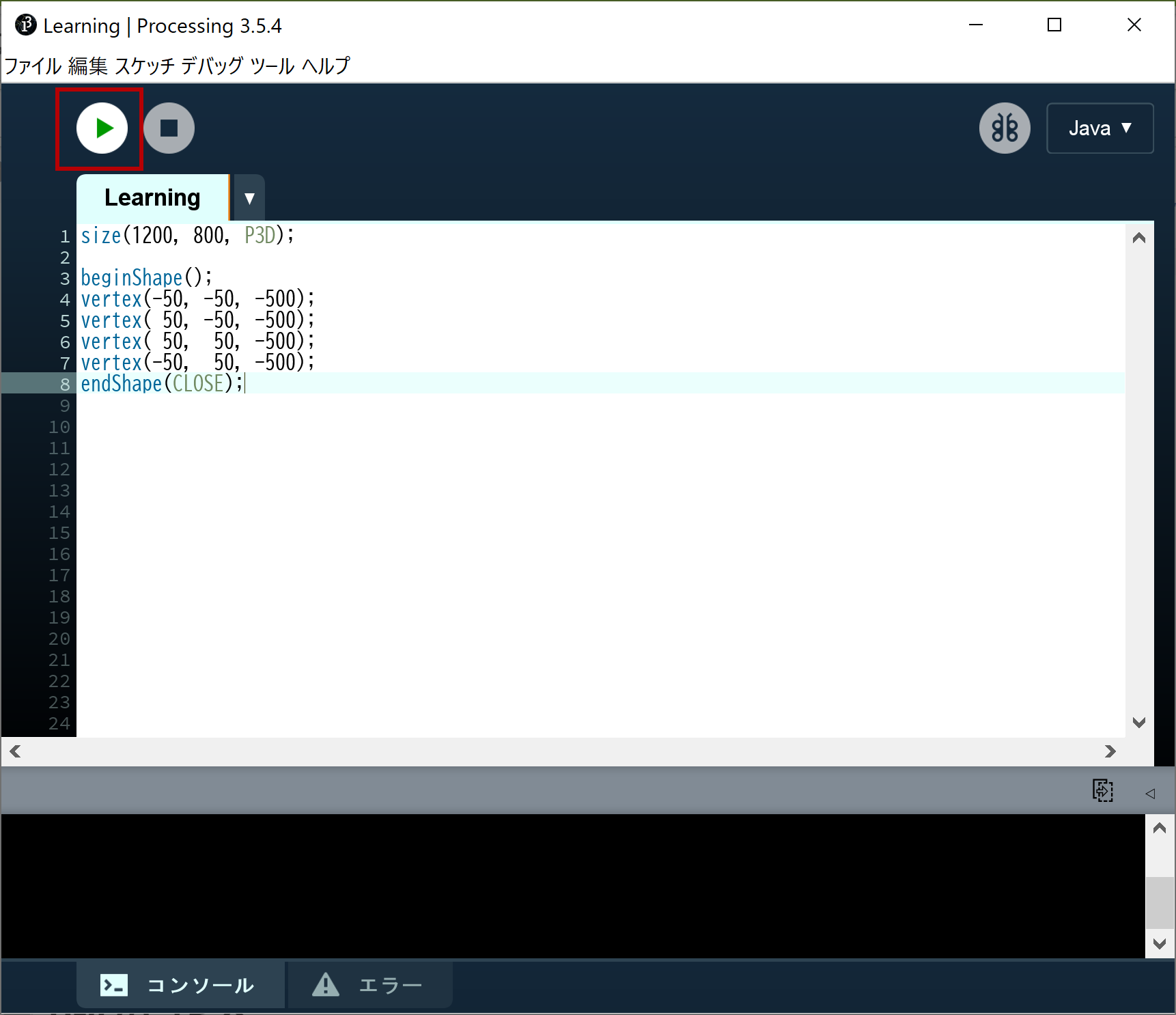
パダワン「お!動いた!動いた!」
パダワン「ん?何だこれ???」
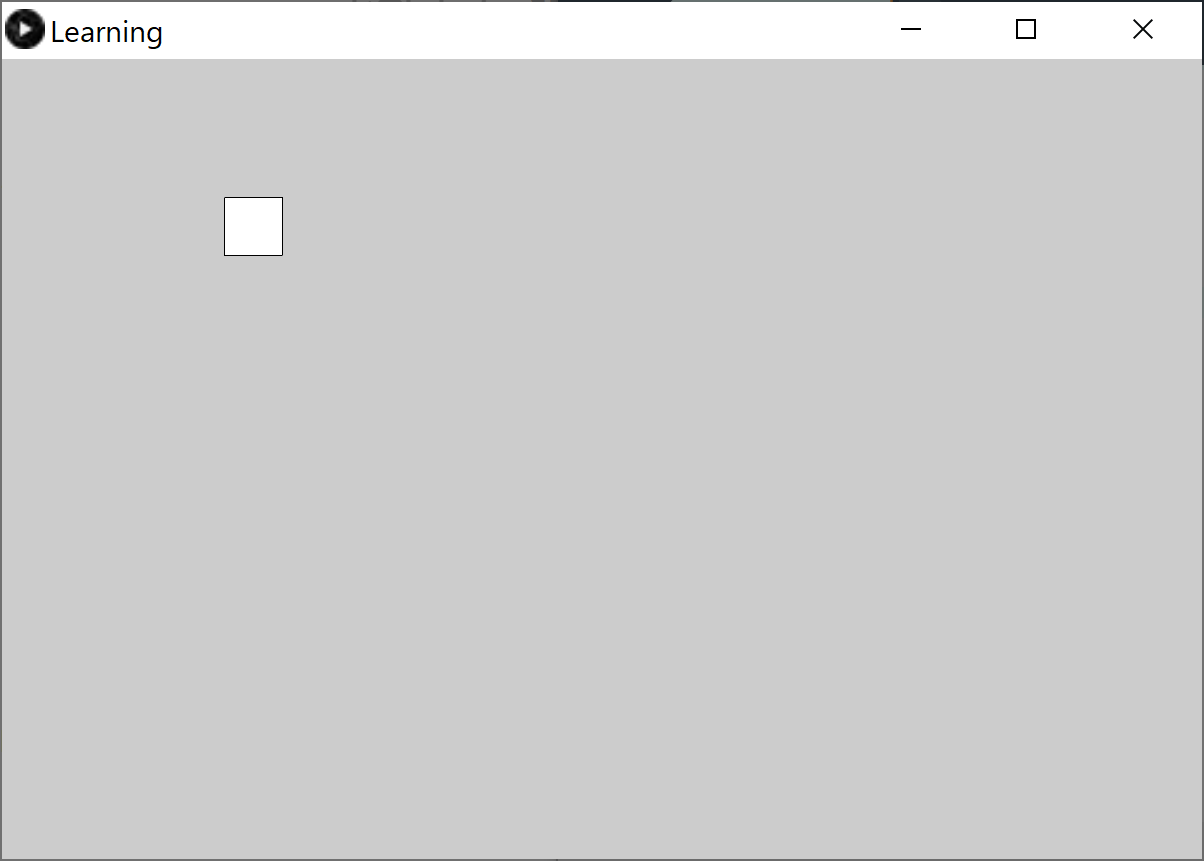
パダワン「ちっこい四角がひとつ …」
パダワン「これじゃ手前だか奥だかわかんないよ!」
パダワン「ダサすぎっしょ、これ!」
午後 10 時|ワールド座標系を制覇する
マスター「そうしたら、ワールド座標系をもっとしっかり捉えるために」
マスター「すこし違う書き方をしてみる」
22 時 00 分|後々のアニメーションための準備
マスター「次のコードを入力するんだ」
マスター「コピペではなく、なるべく自分の手で入力しろ!」
// setup() はプログラム起動直後に一度だけ呼び出される
void setup() {
size(1200, 800, P3D); // ウィンドウサイズと 3DCG の指定
frameRate(24); // フレームレート (fps)
}
// draw() はプログラムの終了まで何度も呼び出される
// (fps==24 の場合は、1秒間に24回呼び出される)
void draw() {
background(255, 255, 255); // 背景色(R,G,B) は白
// ここから下はさっきと同じ
beginShape();
vertex(-50, -50, -500);
vertex( 50, -50, -500);
vertex( 50, 50, -500);
vertex(-50, 50, -500);
endShape(CLOSE);
}
パダワン(Vim じゃないと入力しづらいなぁ)
マスター「この意味を説明する」
-
void setup() {...}
これはセーバーの起動直後に1度だけ呼び出されるメソッドだ。-
size(1200, 800, P3D);
これはさっきと同じだ。
size() メソッドは、setup() の中に書くんだ。 -
frameRate(24);
これは新たに追加する行だ。
アニメーションで 1 秒間に表示するコマ数、つまりフレームレート (fps: frames per second) の指定だ。
-
-
void draw() {...}
これはプログラムの終了まで何度も呼び出されるメソッドだ。
フレームレートを 24 に設定したから、このプログラムの場合は 1 秒間に 24 回呼び出されることになる。-
background(255, 255, 255);
ここで背景色を白に指定している。パラメータは、R(赤)、G(緑)、B(青)の順に指定するんだ。 -
beginShape();
これ以降は、さっきと同じだ。
-
マスター「実行ボタンをクリックしてみるんだ」
パダワン「げっ、背景白くしたらさっきより地味になった …」

パダワン「さっきより分かりづらいし …」
22 時 20 分|描画オブジェクトをメソッドに分離する
マスター「少し分かりやすくしよう」
マスター「次のように修正するんだ」
// setup() はプログラム起動直後に一度だけ呼び出される
void setup() {
size(1200, 800, P3D); // ウィンドウサイズと 3DCG の指定
frameRate(24); // フレームレート (fps)
}
// draw() はプログラムの終了まで何度も呼び出される
// (fps==24 の場合は、1秒間に24回呼び出される)
void draw() {
background(255, 255, 255); // 背景色(R,G,B) は白
updateObject1();
}
// (1) 矩形の描画(静止)
void updateObject1() {
fill(240, 240, 240); // 塗りつぶし色(R,G,B)
stroke(255, 0, 255); // 枠線の色(R,G,B)
strokeWeight(2); // 枠線の太さ
beginShape();
vertex(-50, -50, -500);
vertex( 50, -50, -500);
vertex( 50, 50, -500);
vertex(-50, 50, -500);
endShape(CLOSE);
}
マスター「変更点は次の通りだ」
-
void updateObject1() {...}
まずは、beginShape()~endShape()をこのメソッドに切り分けた。
次に、このメソッド内に次の3行を追記した。-
fill(240, 240, 240);
描画オブジェクトの塗りつぶし色の指定。
ここでは明るいグレーにしておく。 -
stroke(255, 0, 255);
描画オブジェクトの枠線の色を指定。
マゼンタにしておく。 -
strokeWeight(2);
描画オブジェクトの枠線の太さを指定。
少し太目の2にしておく。
-
-
void draw() {...}
background()の呼び出しと、新規に作成した updateObject1() の呼び出しだけだ。
パダワンは [実行ボタン] をクリックした。

パダワン「たいして派手になってないし …」
22 時 40 分|開発ユーティリティの導入
マスター「これから、これをもっと分かりやすくするぞ」
マスター「IDE の [▼]ボタンをクリックして、[新規タブ] を選ぶんだ」
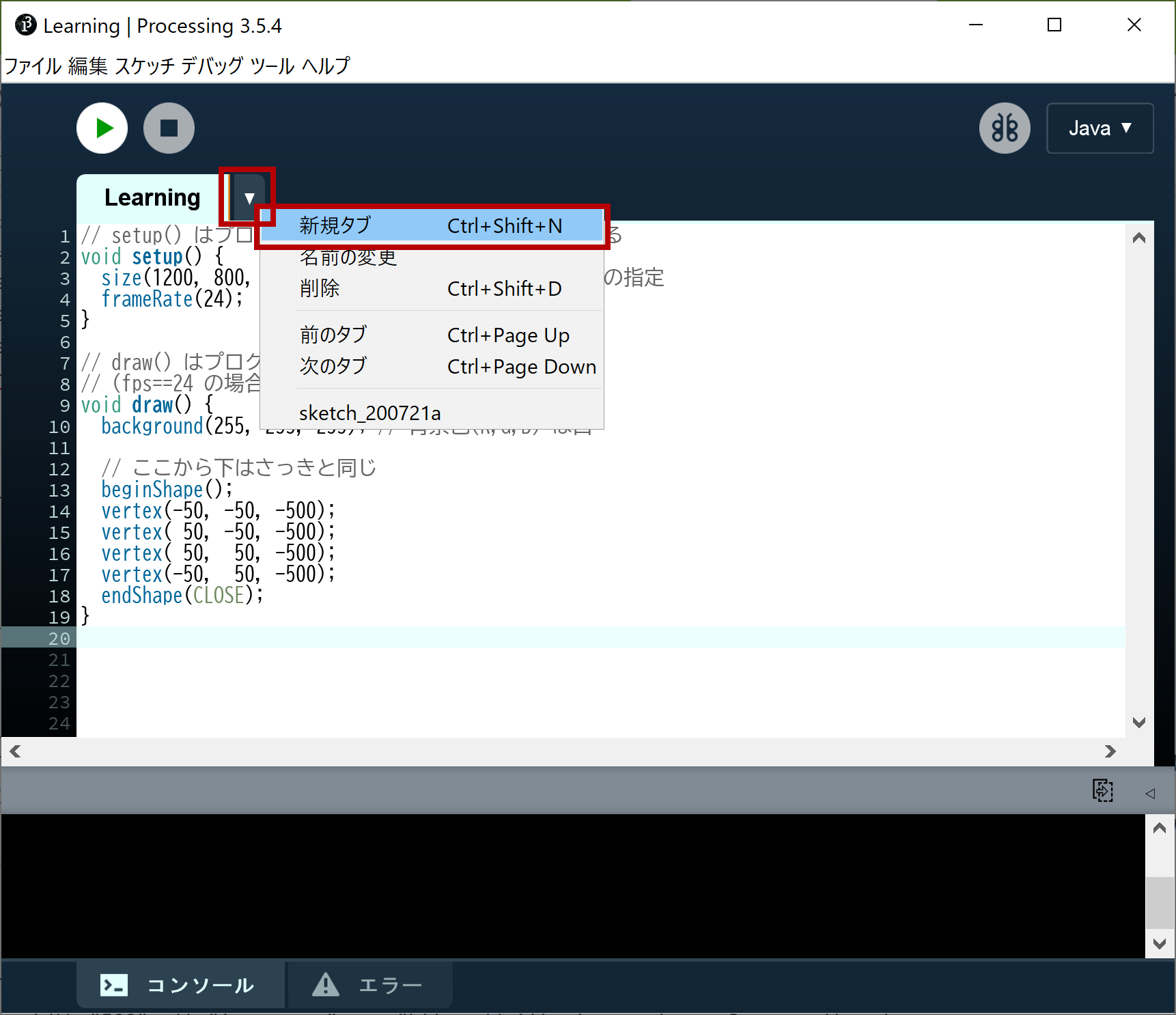
マスター「[新規名] ダイアログが開いたら、"DevUtils" と入力し、[OK] をクリックするんだ」
(名前は何でも良い)
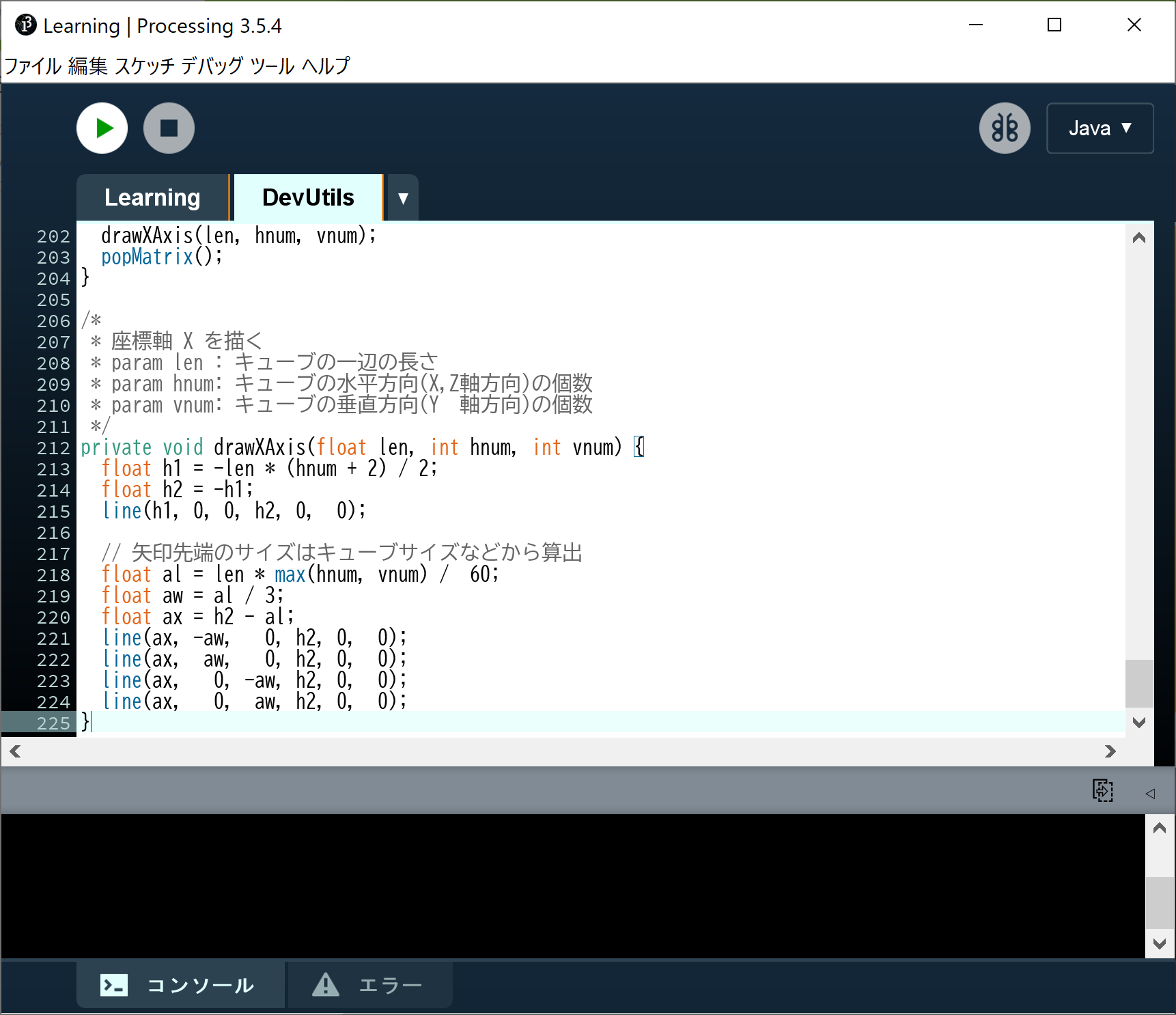
マスター「新しく作成されたタブ [DevUtils] に次のコードをコピペするんだ」
マスター「ひとまず内容は理解しなくて良い。何も考えずにコピペするんだ!」
DevUtils.pde のコードを展開
// Processing Utility DevRoom
// (c) 2020 y-bash
// This software is released under the MIT License.
// http://opensource.org/licenses/mit-license.php
public void setupDevRoom(float len, int hnum, int vnum) {
float radius = len * hnum * 1.25;
float depth = len * vnum / 2;
int period = 16;
setupDevRoom(len, hnum, vnum, radius, depth, period);
}
public void setupDevRoom(float len, int hnum, int vnum,
float radius, float depth, int period) {
gCubeSideLength = abs(len);
gCubeHNum = (hnum >= 0) ? hnum : 0;
gCubeVNum = (vnum >= 0) ? vnum : 0;
setCameraOrbitalRadius(radius);
setCameraMaxDepth(depth);
setCameraOrbitalPeriod(period);
}
public void setDevRoomAutoCameraEnabled(boolean isEnabled) {
gIsCameraEnabled = isEnabled;
}
public void setDevRoomVisible(boolean isVisible) {
gIsDevRoomVisible = isVisible;
}
public void setCameraOrbitalRadius(float radius) {
if (radius == 0.0) radius = 0.1;
gCameraOrbitalRadius = radius;
}
public void setCameraMaxDepth(float depth) {
gCameraMaxDepth = depth;
}
public void setCameraOrbitalPeriod(int period) {
if (period == 0 ) period = 1;
gCameraOrbitalPeriod = period * 1000;
}
public void updateDevRoom() {
pushStyle();
if (gIsCameraEnabled ) updateCamera();
if (gIsDevRoomVisible) drawDevRoom(gCubeSideLength, gCubeHNum, gCubeVNum);
popStyle();
}
public void mouseClicked() {
gIsDevRoomVisible = !gIsDevRoomVisible;
}
private boolean gIsDevRoomVisible = true;
private boolean gIsCameraEnabled = true;
private float gCubeSideLength = 200;
private int gCubeHNum = 4;
private int gCubeVNum = 2;
private float gCameraOrbitalRadius = 1000;
private float gCameraMaxDepth = 200;
private int gCameraOrbitalPeriod = 16000;
private void updateCamera() {
int ms = millis();
float hAngle = TWO_PI * ms / gCameraOrbitalPeriod;
float x = gCameraOrbitalRadius * sin(hAngle);
float z = gCameraOrbitalRadius * cos(hAngle);
float y = sin(hAngle) * gCameraMaxDepth;
camera(x, y, z, 0, 0, 0, 0, 1, 0);
}
private void drawDevRoom(float len, int hnum, int vnum) {
strokeWeight(1);
stroke(214, 214, 214);
drawCubes(len, hnum, vnum);
strokeWeight(3);
drawFloor(0, len, hnum);
drawAxes(len, hnum, vnum);
}
private void drawCubes(float len, int hnum, int vnum) { float v1 = -len * vnum / 2;
for (int i = 0; i <= vnum; i++) {
float y = v1 + i * len;
drawFloor(y, len, hnum);
}
float h1 = -len * hnum / 2;
float v2 = -v1;
for (int i = 0; i <= hnum; i++) {
float x = h1 + i * len;
for (int j = 0; j <= hnum; j++) {
float z = h1 + j * len;
line(x, v1, z, x, v2, z);
}
}
}
private void drawFloor(float y, float len, int num) {
float h1 = -len * num / 2;
float h2 = -h1;
for (int i = 0; i <= num; i++) {
float cp = h1 + i * len;
line(h1, y, cp, h2, y, cp);
line(cp, y, h1, cp, y, h2);
}
}
private void drawAxes(float len, int hnum, int vnum) {
strokeWeight(2);
stroke(255, 0, 0);
drawXAxis(len, hnum, vnum);
stroke(0, 255, 0);
pushMatrix();
rotateZ(0.5 * PI);
drawXAxis(len, hnum, vnum);
popMatrix();
stroke(0, 0, 255);
pushMatrix();
rotateY(-0.5 * PI);
drawXAxis(len, hnum, vnum);
popMatrix();
}
private void drawXAxis(float len, int hnum, int vnum) {
float h1 = -len * (hnum + 2) / 2;
float h2 = -h1;
line(h1, 0, 0, h2, 0, 0);
float al = len * max(hnum, vnum) / 60;
float aw = al / 3;
float ax = h2 - al;
line(ax, -aw, 0, h2, 0, 0);
line(ax, aw, 0, h2, 0, 0);
line(ax, 0, -aw, h2, 0, 0);
line(ax, 0, aw, h2, 0, 0);
}
パダワン「コピペは大得意だぜ!銀河イチさ」
マスター「貼り付けたら、次のように、」
マスター「Learning タブ内の draw() メソッドに1行追加するんだ」
...
void draw() {
background(255, 255, 255); // 背景色(R,G,B) は白
updateDevRoom(); // <===== 追記 =====
updateObject1();
}
...
updateDevRoom(); を updateObject1(); の前に追記し、パダワンは [実行ボタン] をクリックした。
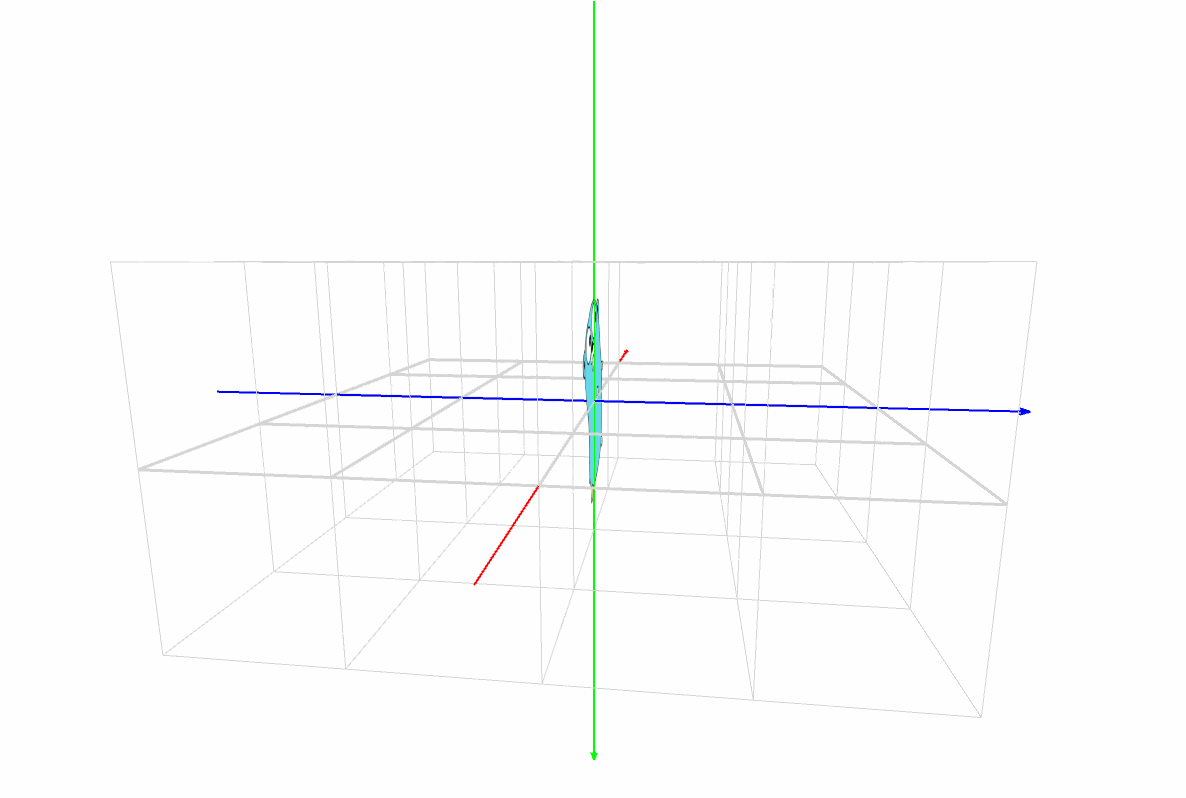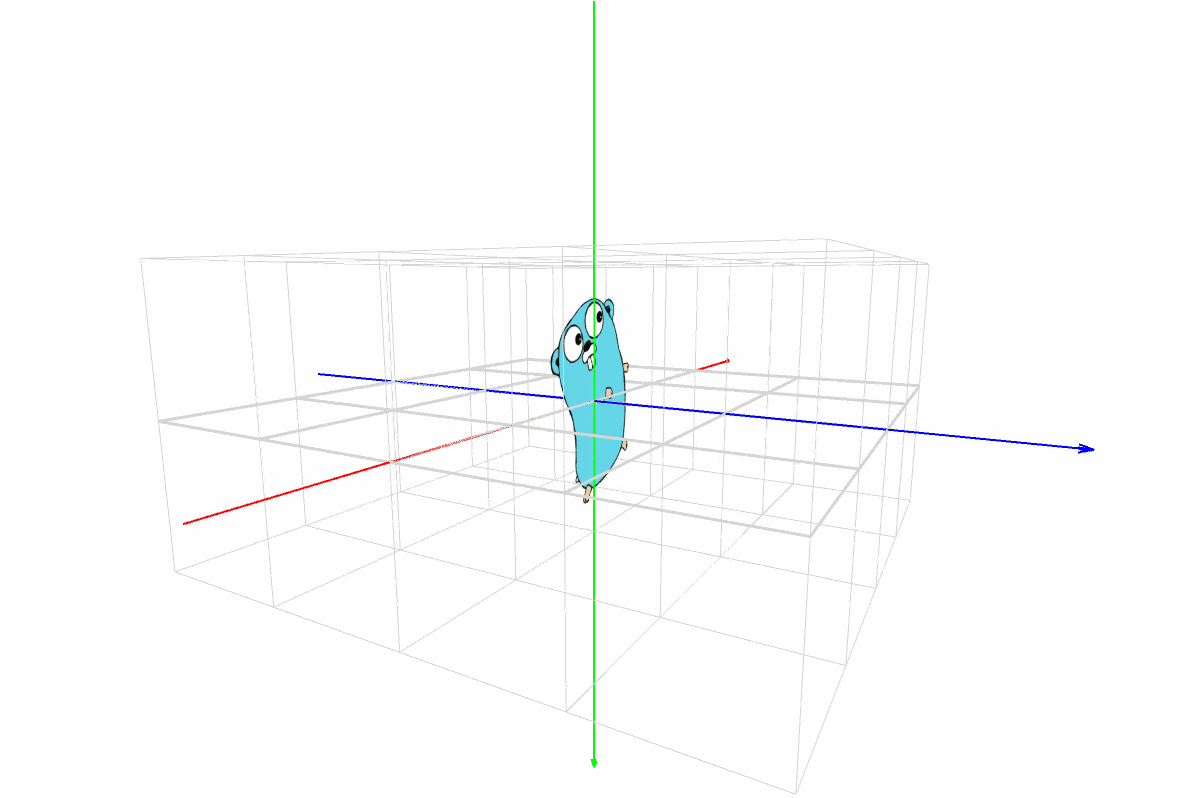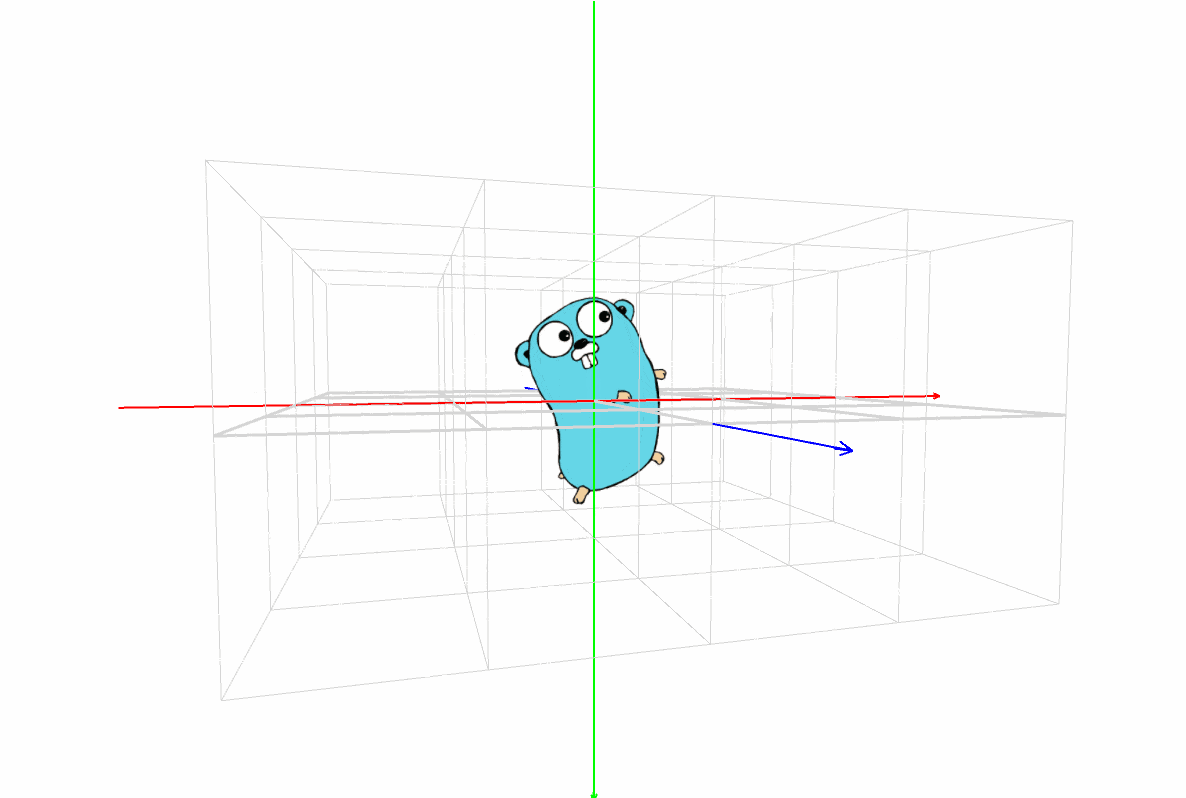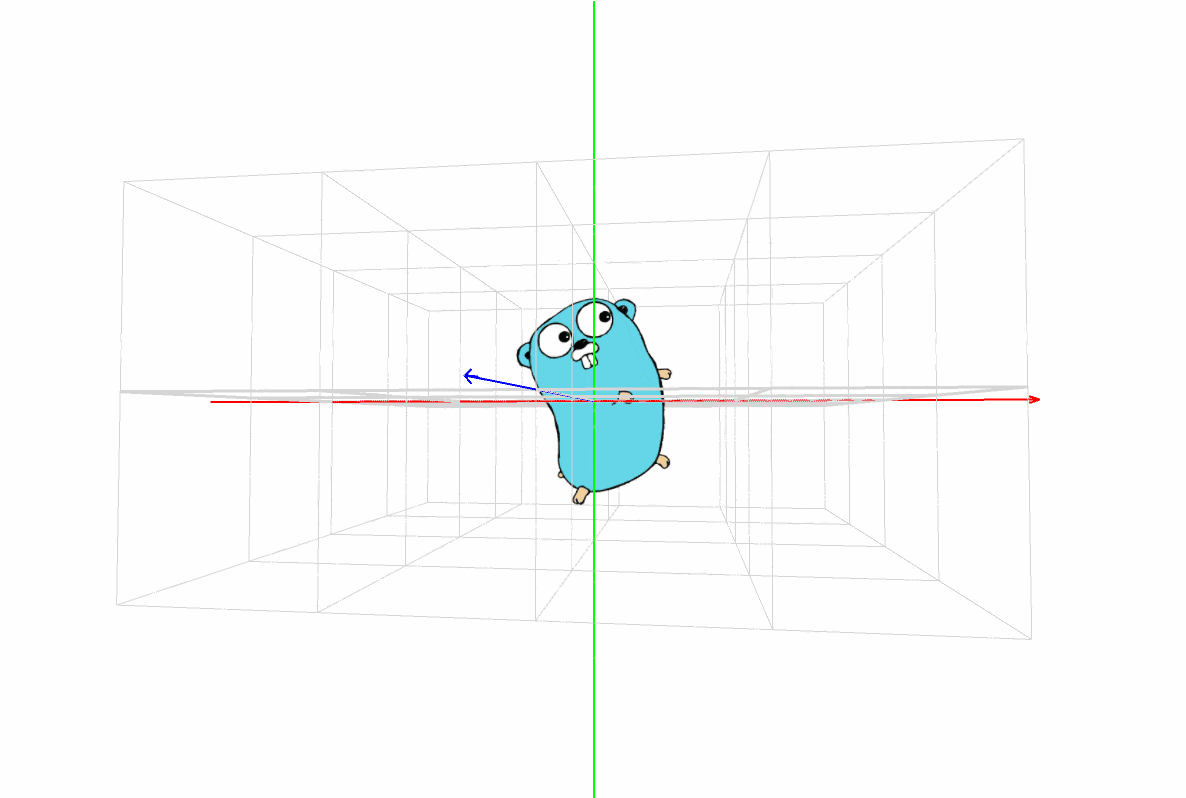
パダワン「お、なんか回ってる …」
 (容量節約のためにコマ送りにしていますが、実際のプログラムではもっとスムーズに動きます)
(容量節約のためにコマ送りにしていますが、実際のプログラムではもっとスムーズに動きます)
マスター「実は、この中の物はどれも静止している」
パダワン「え??? だって回ってんじゃん!」
マスター「回っているのは、カメラなんだ」
マスター「カメラの視点を変えると、立体物の形がよくわかるだろ?」
パダワン「なるほど …」
マスター「このユーティリティは、開発初期の手間を低減するものだ」
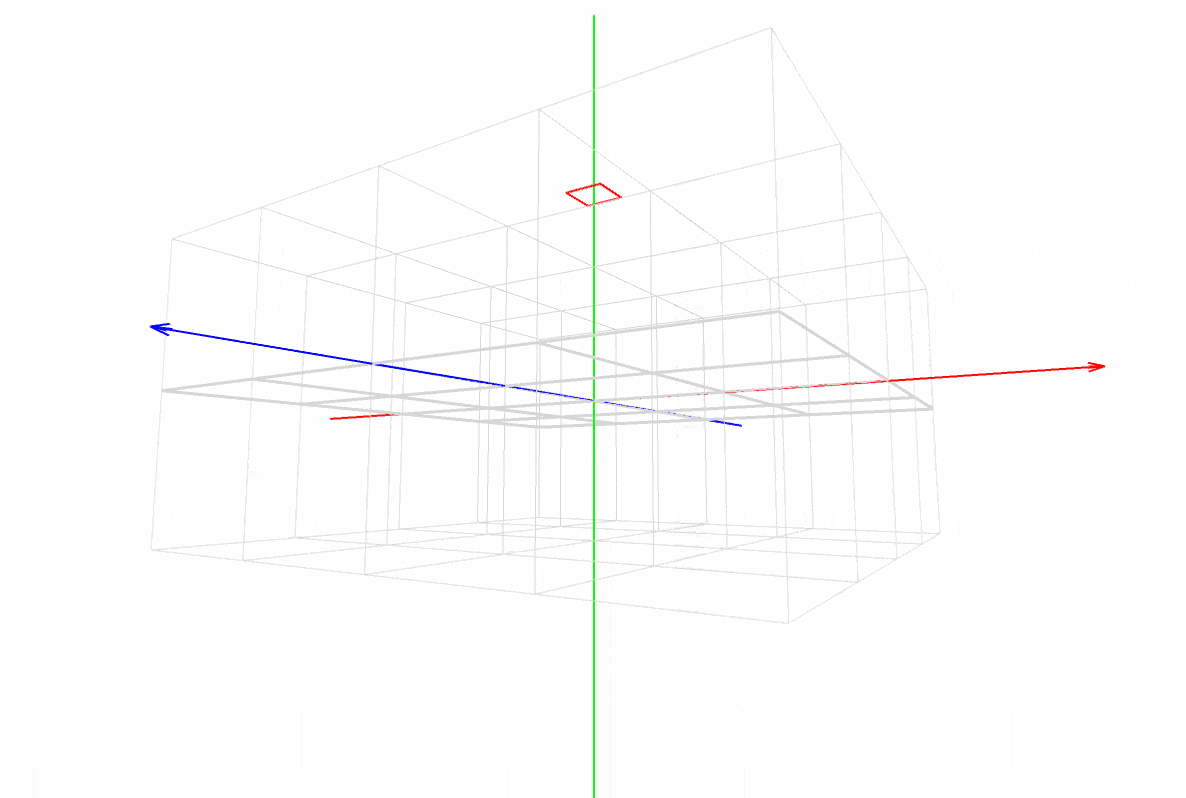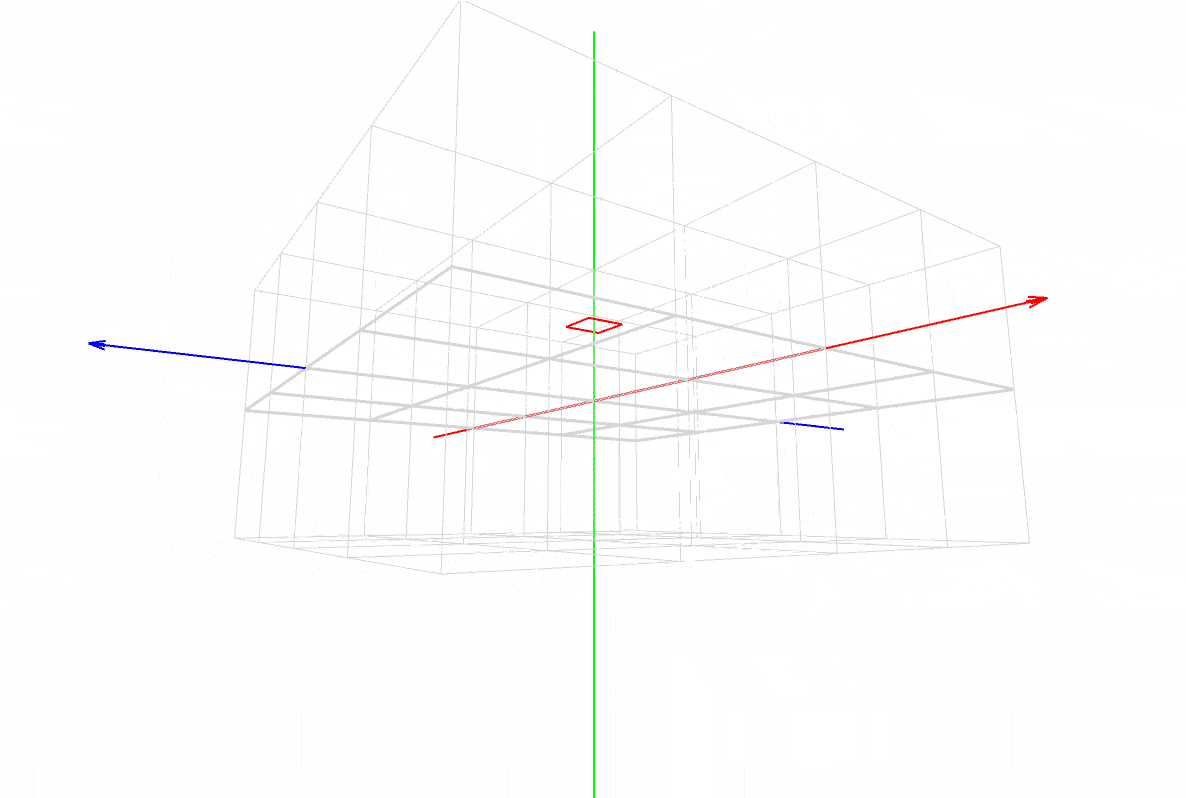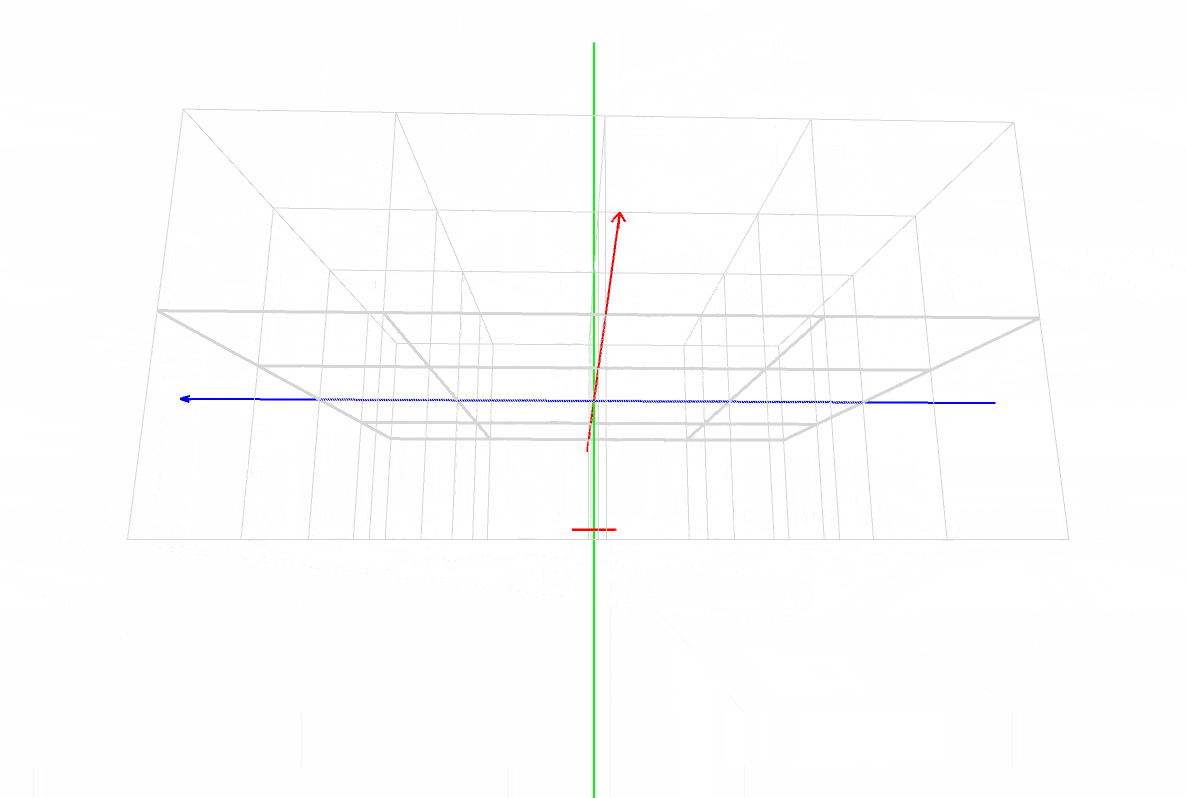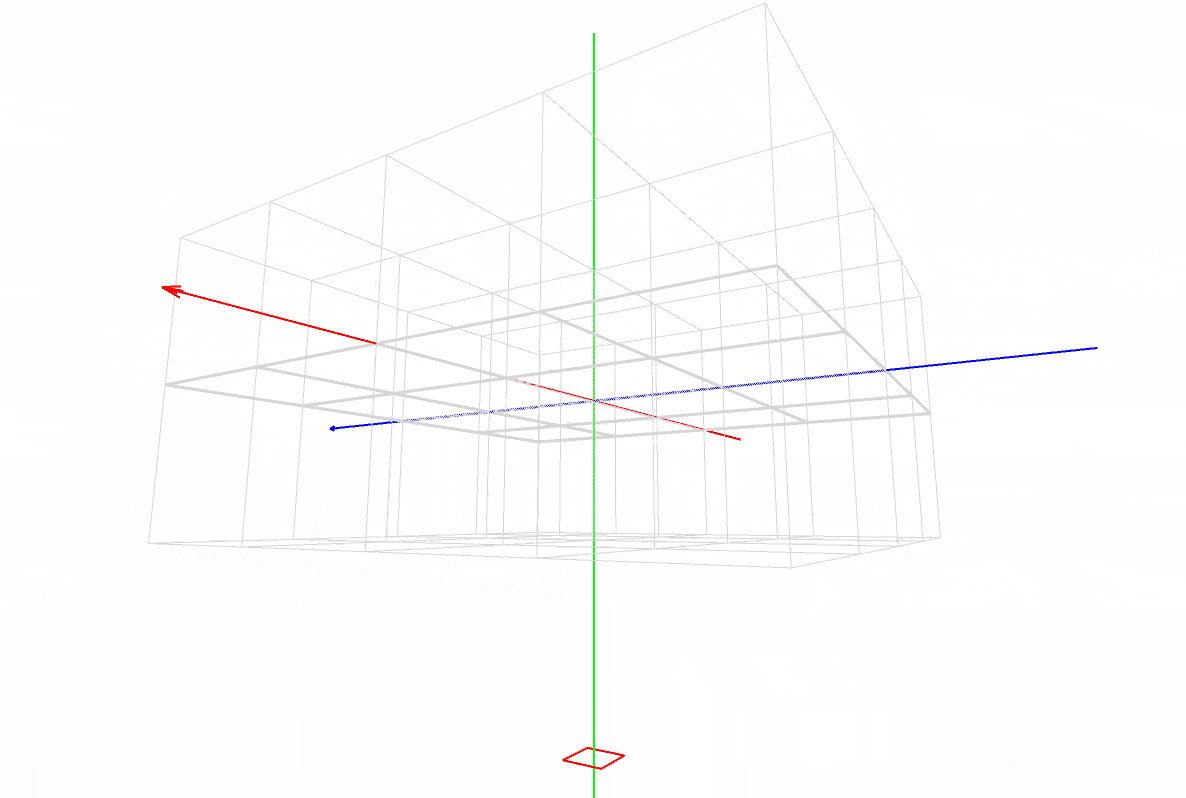
マスター「見方だが、まず X, Y, Z の座標軸があるだろ?」
マスター「その3本が交差した点が原点(0, 0, 0) だ」
マスター「色は覚えてるか?」
パダワン「うん。赤は X 軸で左から右で、」
パダワン「緑は Y 軸で上から下で、」
パダワン「青は Z 軸で正面の遠い方からこっちに向いて …」
パダワン「あ、ほんとだ。矢印の方向が合ってる!」
マスター「次に、立方体の箱が並んでるだろ?」
マスター「水平方向に 4 x 4 個、垂直方向に 2 段になってるから」
マスター「全部で32個のキューブで構成されてるんだ」
マスター「キューブの 1 辺の長さは 200 だ」
マスター「それを頭に入れて、自分が描画した矩形を見てみるんだ」
パダワン「えーと、キューブ 2 個で 400だから …」
パダワン「紫の四角が、、」
パダワン「あ、-400 よりちょっと遠くで z 軸に刺さってる!」
マスター「そうだ。大体の位置が掴めるだろう?!」
マスター「また、画面をクリックすると、」
マスター「キューブや座標軸が表示されなくなるぞ」
パダワン「あ、ほんとだ。なんか地味(笑)」
マスター「もう一度、クリックすれば元に戻る」
パダワン「おお、戻った。戻った」
午後 11 時|オブジェクトを動かす
23 時 00 分|まっすぐ動かす
マスター「今度は以下のようにセーバーを書き換えるんだ!」
// setup() はプログラム起動直後に一度だけ呼び出される
void setup() {
size(1200, 800, P3D); // ウィンドウサイズと 3DCG の指定
frameRate(24); // フレームレート (fps)
}
// draw() はプログラムの終了まで何度も呼び出される
// (fps==24 の場合は、1秒間に24回呼び出される)
void draw() {
background(255, 255, 255); // 背景色(R,G,B) は白
updateDevRoom();
//updateObject1(); // <===== コメントアウト =====
updateObject2(); // <===== 追記 =====
}
// (1) 矩形の描画(静止)
void updateObject1() {
fill(240, 240, 240); // 塗りつぶし色(R,G,B)
stroke(255, 0, 255); // 枠線の色(R,G,B)
strokeWeight(2); // 枠線の太さ
beginShape();
vertex(-50, -50, -500);
vertex( 50, -50, -500);
vertex( 50, 50, -500);
vertex(-50, 50, -500);
endShape(CLOSE);
}
// (2) 矩形の描画(疑似等速直線運動) // <===== これ以降追記↓ =====
float gZ = -600;
void updateObject2() {
gZ+=10; // Z座標の更新
fill(255, 255, 255); // 塗りつぶし色(R,G,B)
stroke(0, 255, 255); // 枠線の色(R,G,B)
strokeWeight(2); // 枠線の太さ
beginShape();
vertex(-40, -40, gZ);
vertex( 40, -40, gZ);
vertex( 40, 40, gZ);
vertex(-40, 40, gZ);
endShape(CLOSE);
}
パダワン「えーと、、」
パダワン「updateObject2() を作って、」
パダワン「draw() の中から呼び出して、」
パダワン「updateObject1() をコメント …」
パダワン(くそっ、コピペしてえ!)
マスター「説明する」
-
float gZ = -600;
グローバル変数 gZ を作って、-600 で初期化する。
gZ はオブジェクトの Z 座標の位置を格納するんだ。 -
gZ+=10;
オブジェクトが描画される度に値が 10 ずつ増えるようにする。 -
vertex(-40, -40, gZ);以降
頂点を描画する時に Z 座標の値に gZ を指定する。
パダワンは [実行] ボタンをクリックした。
マスター「だが、この実装方法には問題がある」
マスター「フレームレートを 12 にして実行してみるんだ」
...
frameRate(12);
...
パダワン「あ、ノロノロしてる …」
マスター「そうだ。この実装方法はフレームレートに影響を受けてしまうんだ」
23 時 20 分|フレームレートに影響されずに動かす
マスター「以下を入力するんだ」
マスター「一部省略してあるから注意するんだ」
...
void draw() {
...
//updateObject2(); // <===== コメントアウト =====
updateObject3(); // <===== 追記 =====
}
...
// (3) 矩形の描画(リアル等速直線運動) // <===== これ以降追記↓ =====
void updateObject3() {
final float START_Y = -600; // 開始時点のY座標
final float SPEED = 200; // 秒速
float ms = millis(); // プログラム開始時点からの経過ミリ秒
float dy = ms * SPEED / 1000; // 移動距離(Y座標)
float y = START_Y + dy; // 現在位置(Y座標)
noFill(); // 塗りつぶしなし
stroke(255, 0, 0); // 枠線の色(R,G,B)
strokeWeight(2); // 枠線の太さ
beginShape();
vertex(-30, y, -30);
vertex( 30, y, -30);
vertex( 30, y, 30);
vertex(-30, y, 30);
endShape(CLOSE);
}
パダワン「えーと、前と同じように updateObject2() をコメントして、」
パダワン「updateObject3() を作って draw() から呼び出す …」
マスター「説明する」
-
final float START_Y = -600;
開始時点のオブジェクトの Y 座標だ。 -
final float SPEED = 200;
スピード(秒速)だ。このオブジェクトは 1 秒間に 200 進む。 -
float ms = millis();
セーバーが起動した時点からの経過ミリ秒を得る関数だ。 -
float dy = ms * SPEED / 1000;
セーバーが起動した時点からの移動距離だ。 -
float y = START_Y + dy;
オブジェクトの現在位置(Y 座標)だ。 -
noFill();
オブジェクトを塗りつぶさないという指定だ。 -
vertex(-30, y, -30);
頂点の指定で Y 座標の値に変数 y を指定して、時間経過と共に、オブジェクトが上から下へ毎秒 200 だけ (1 ミリ秒あたり 0.2 だけ) 進むようにしている。
パダワン「上から下に動くだけで、あんま変わんない …」
マスター「フレームレートをいろいろ変えてみるんだ」
マスター「時間あたりの移動量に違いがないことがわかるだろう」
マスター「最後にフレームレートを戻しておくのを忘れるな!」
...
frameRate(24);
...
23 時 40 分|円軌道に乗せる
マスター「次はこうするんだ!」
...
void draw() {
...
//updateObject3(); // <===== コメントアウト =====
updateObject4(); // <===== 追記 =====
}
...
// (4) 矩形の描画(円運動) // <===== これ以降追記↓ =====
void updateObject4() {
final float R = 500; // 公転半径
final float SPEED = 60; // 角度(Degree)/秒
float ms = millis(); // プログラム開始時点からの経過ミリ秒
float dd = ms * SPEED / 1000; // 移動角度(Degree)
float dr = radians(dd); // 移動角度(Radian)
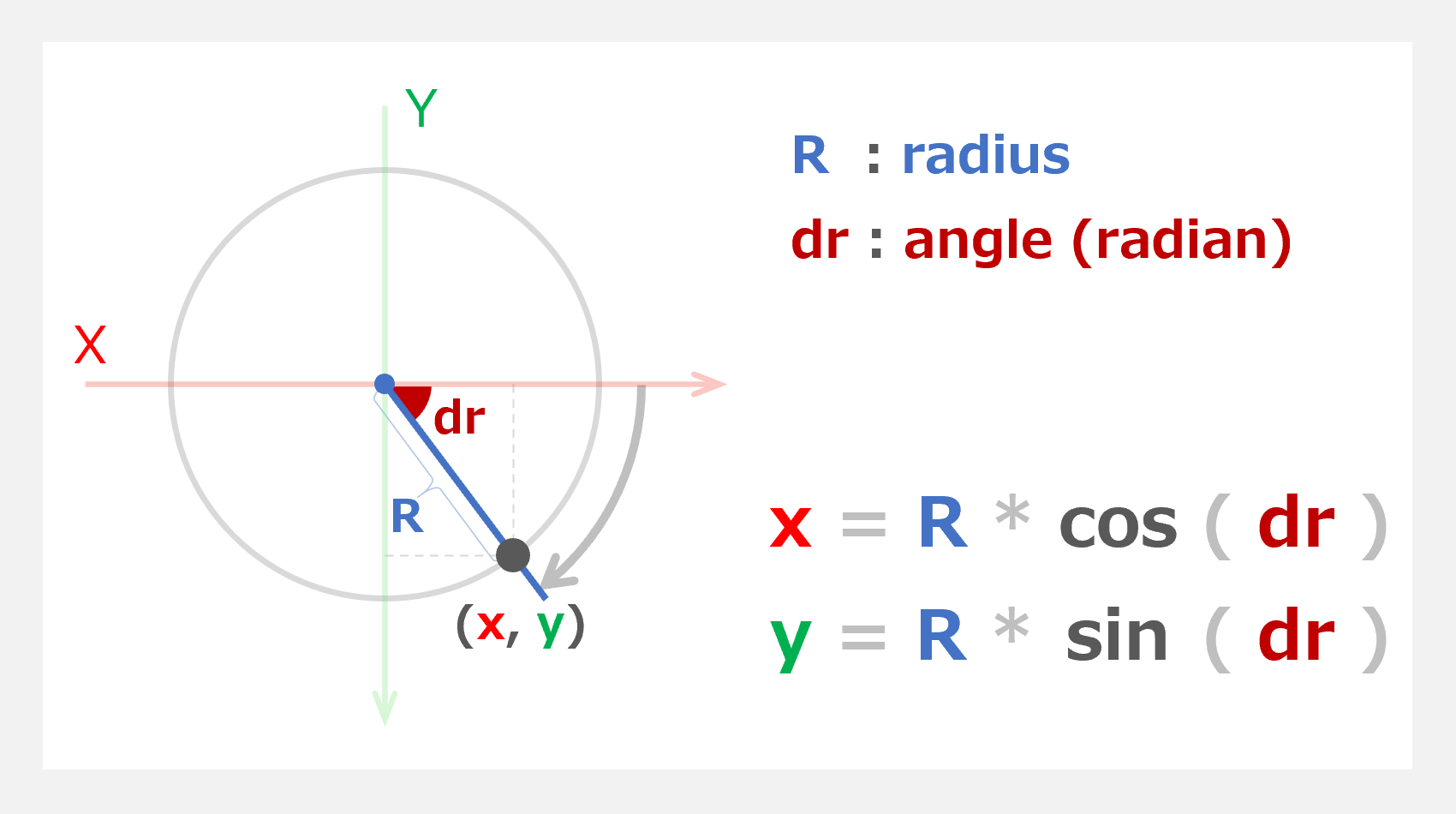
float x = R * cos(dr); // X座標
float y = R * sin(dr); // Y座標
fill(255, 255, 255); // 塗りつぶし色(R,G,B)
stroke(0, 0, 255); // 枠線の色(R,G,B)
strokeWeight(2); // 枠線の太さ
beginShape();
vertex(x-30, y, -30);
vertex(x+30, y, -30);
vertex(x+30, y, 30);
vertex(x-30, y, 30);
endShape(CLOSE);
}
マスター「説明する」
-
final float R = 300;
これはオブジェクトの公転半径だ。 -
final float SPEED = 60;
1 秒間に進む角度 (Degree) だ。 -
float ms = millis();
これはもういいな!セーバー開始時点からの経過ミリ秒だ。 -
float dd = ms * SPEED / 1000;
セーバ開始時点から進んだ角度 (Degree) だ。
マスター「あとは三角関数の計算なんだが …」
パダワン「げっ!!!」
パダワン(三角関数苦手だったんだよなぁ …)
パダワン(四角関数になったら頑張ろうと思ってたのに、)
パダワン(イニシエイトじゃ教えてくれなかったし …)
ラジアン(弧度法)
マスター「そしたら簡単におさらいだ」
マスター「まずは『ラジアン』からだな」
マスター「ラジアンは角度の単位だ」
マスター「円周上の弧の長さが」
マスター「その円の半径と等しいときの角度が 1 ラジアンだ」
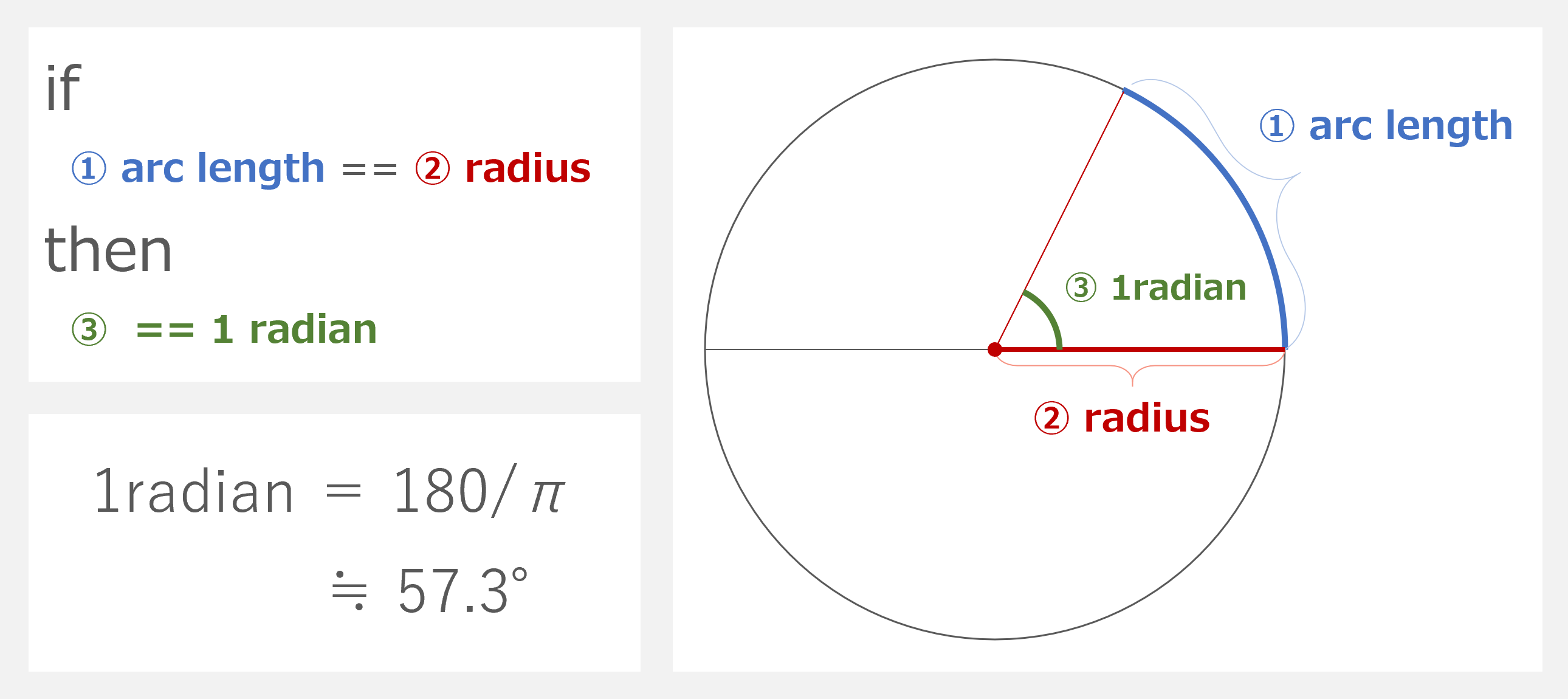
マスター「度数法でいえば、だいたい 57.3度 (degree) くらいだ」
パダワン「なんで、そんな半端な数字なんだよ!」
パダワン「1 ラジアン = 60度 でいいじゃん!」
マスター「まあ、そう言うな …」
マスター「銀河単位系(脚注:国際単位系 SI のこと)で」
マスター「決められた単位なんだ」
マスター「これに約 3.14 を乗ずると 180° になるぞ!」
パダワン「パイ (π) だ!」
パダワン「でもこんなの覚えられないよ!」
マスター「Processing を使う上でこれと特に覚える必要はない」
マスター「だが、Processing のメソッドは、」
マスター「角度をラジアンで指定する必要があるから、」
マスター「度数をラジアンに変換する radians() を使う必要がある」
マスター「これだけは覚えておくんだ」
パダワン「なるほど …」
パダワン「とにかく角度は」
パダワン「radians() に包んで渡せばいいんだね!」
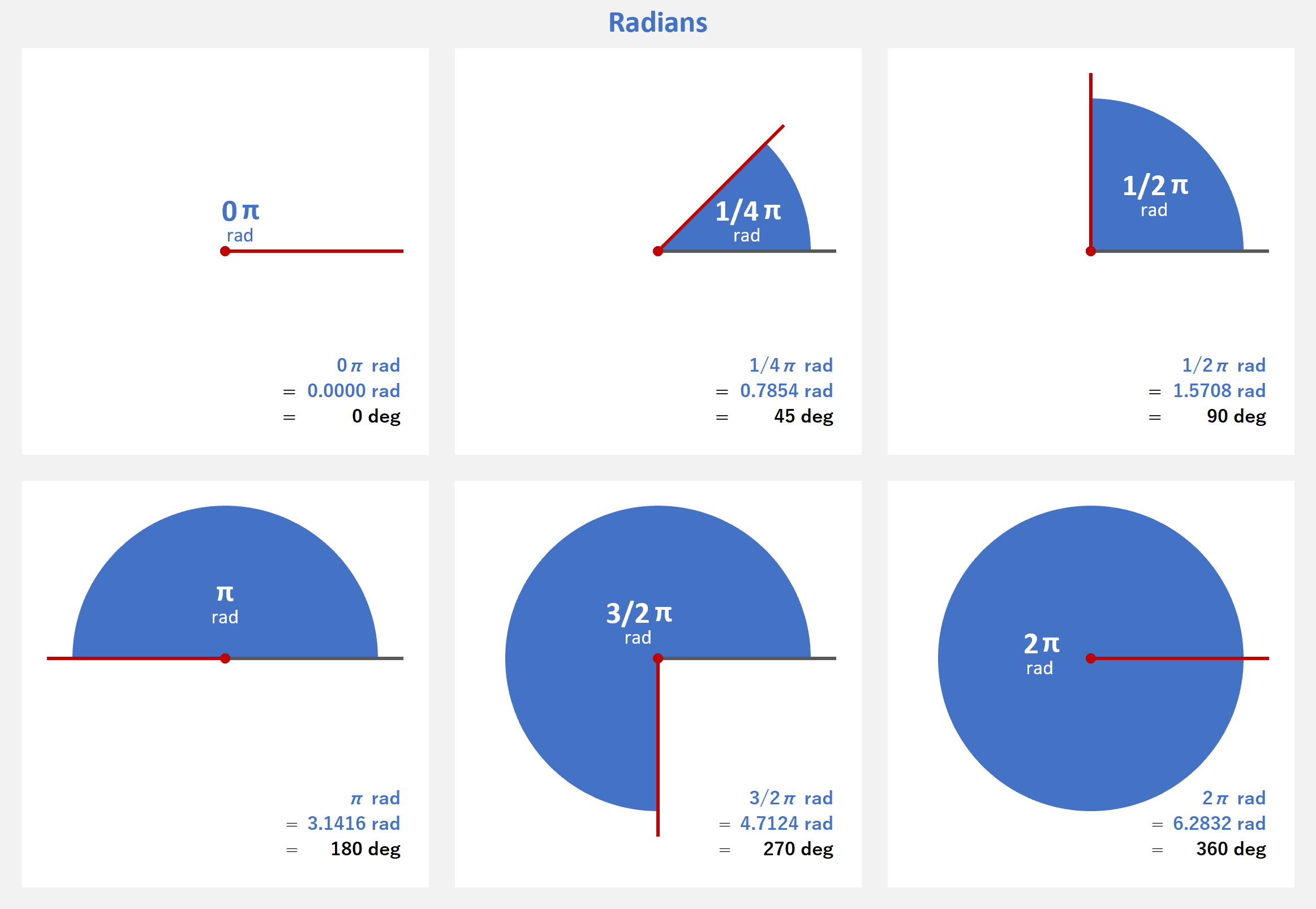
マスター「また、特別な角度に関係する定数が定義されている」
| 定数 | 意味 | 度数 (degree) |
弧度 (radian) |
|---|---|---|---|
| PI | π | 180° | 3.1415927 |
| TWO_PI | 2π | 360° | 6.2831855 |
| HALF_PI | 1/2π | 90° | 1.5707964 |
| QUARTER_PI | 1/4π | 45° | 0.7853982 |
マスター「これも頭に入れておいた方が良いだろう」
パダワン「げっ!さっき『これだけ』って、、」
正弦(sin)、余弦(cos)、ついでに正接(tan)
マスター「次に三角関数だな」
マスター「サイン、コサイン、タンジェントは覚えてるか?」
パダワン「あ!その名前、聞いたことある!」
マスター「それが三角関数だ」
パダワン(えっ? そうだったっけ …)
マスター「どう習ったかはともかくとして、一般的な CG では」
マスター「ある長さ と ある角度 から」
マスター「別の長さ を求める場合に使われることが多いだろう」
マスター「今はサインとコサインしか使わないが、」
マスター「タンジェントもよく使われるから一緒に説明しておこう」
マスター「ひとまず、これらはすべて、」
マスター「長さと角度から別の長さを求めるために」
マスター「使われると覚えておくんだ」
マスター「まずはサイン(正弦)だ。これは、直角三角形の」
マスター「斜辺の長さ から 高さ を求めるために使えるんだ」
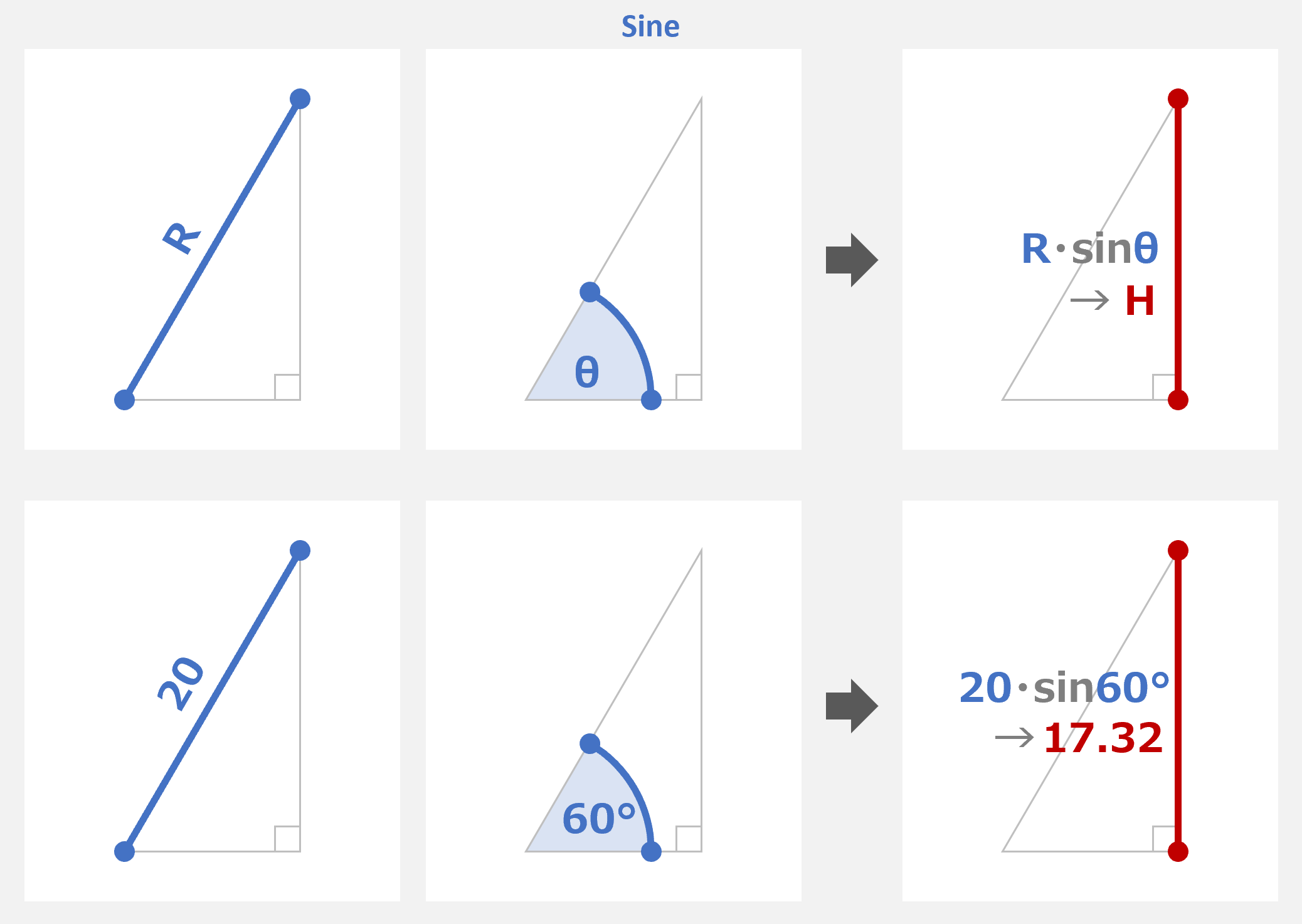
マスター「次にコサイン(余弦)だ。これは、直角三角形の」
マスター「斜辺の長さ から 幅 を求めるために使えるんだ」
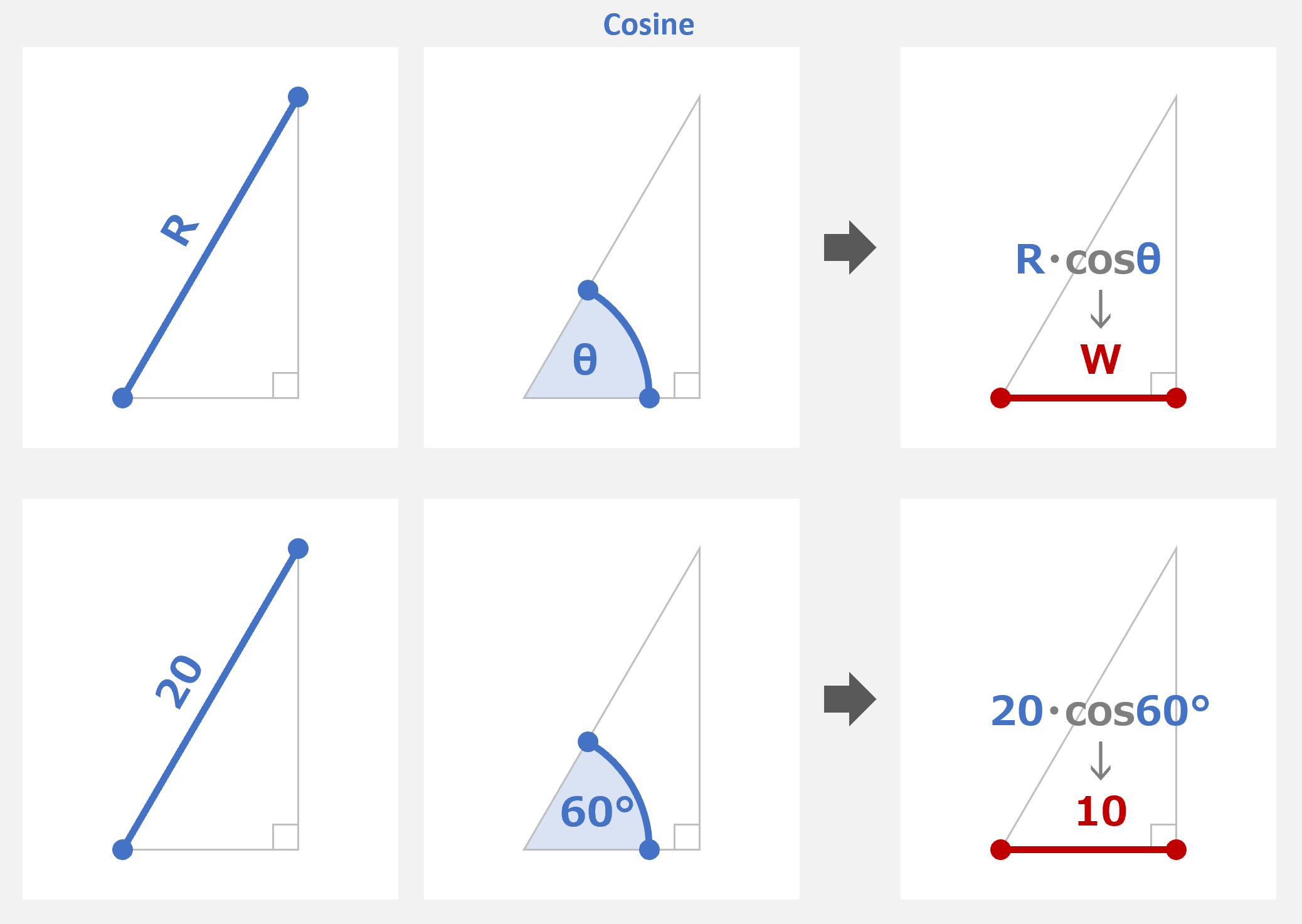
マスター「次にタンジェント(正接)だが、これは 2 つの使い方がある」
マスター「1 つ目は、直角三角形の」
マスター「高さ から 幅 を求めるために使え、」
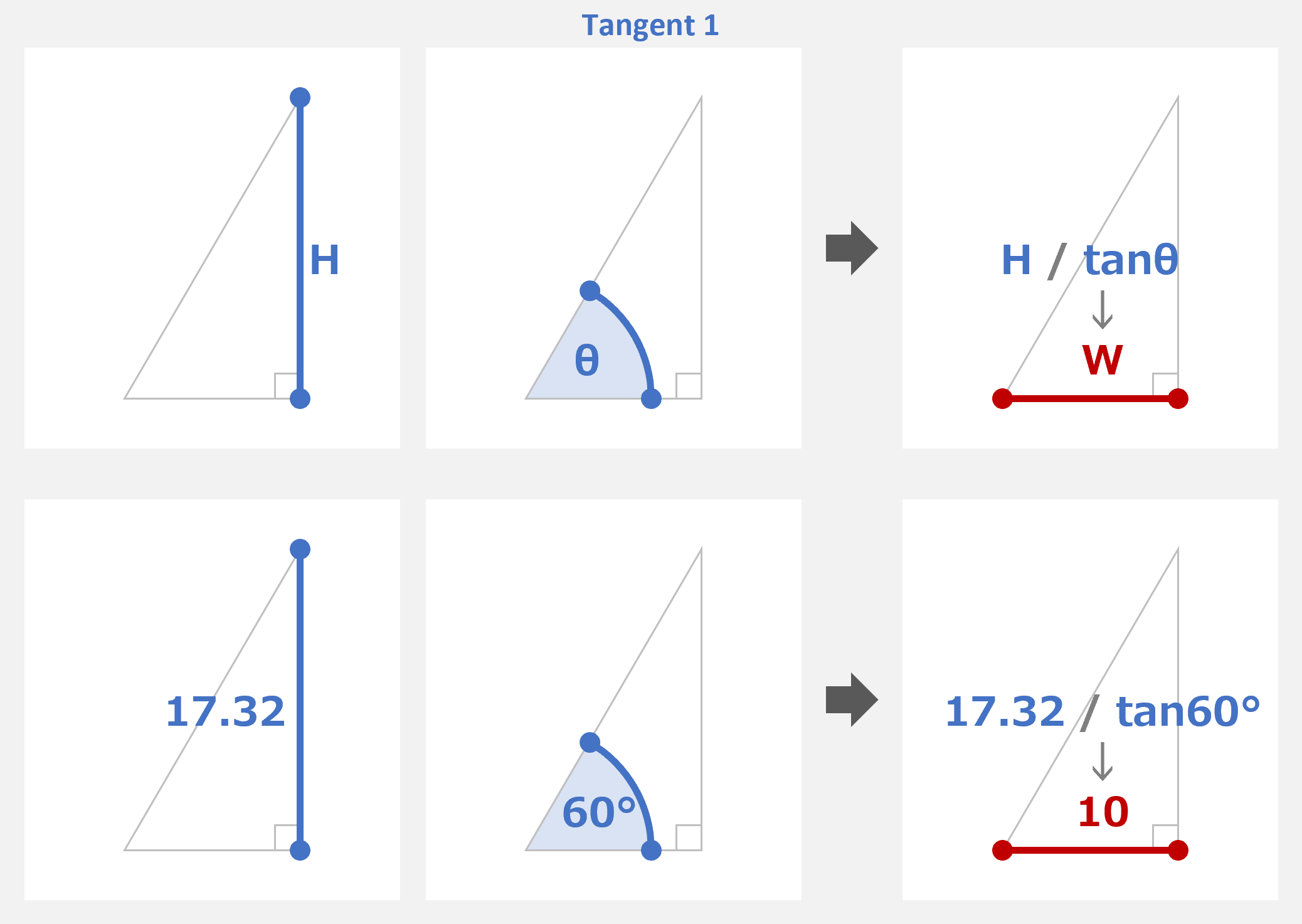
マスター「もう 1 つは、直角三角形の」
マスター「幅 から 高さ を求めるために使えるんだ」
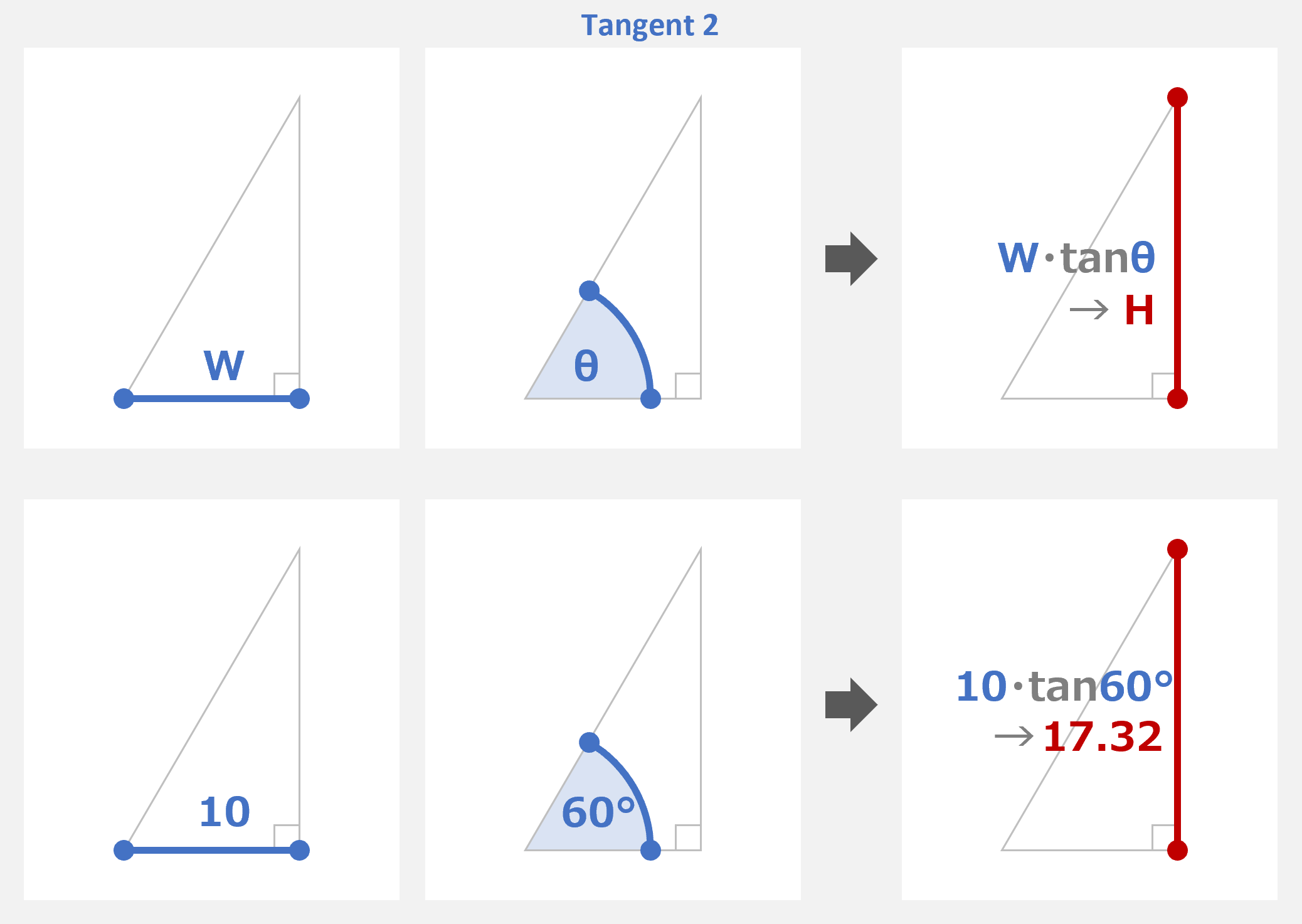
パダワン「えーと、、」
パダワン「斜めからまっすぐを知りたいときは」
パダワン「サインとコサインで …」
パダワン「まっすぐからまっすぐを知りたいときは」
パダワン「タンジェントで …」
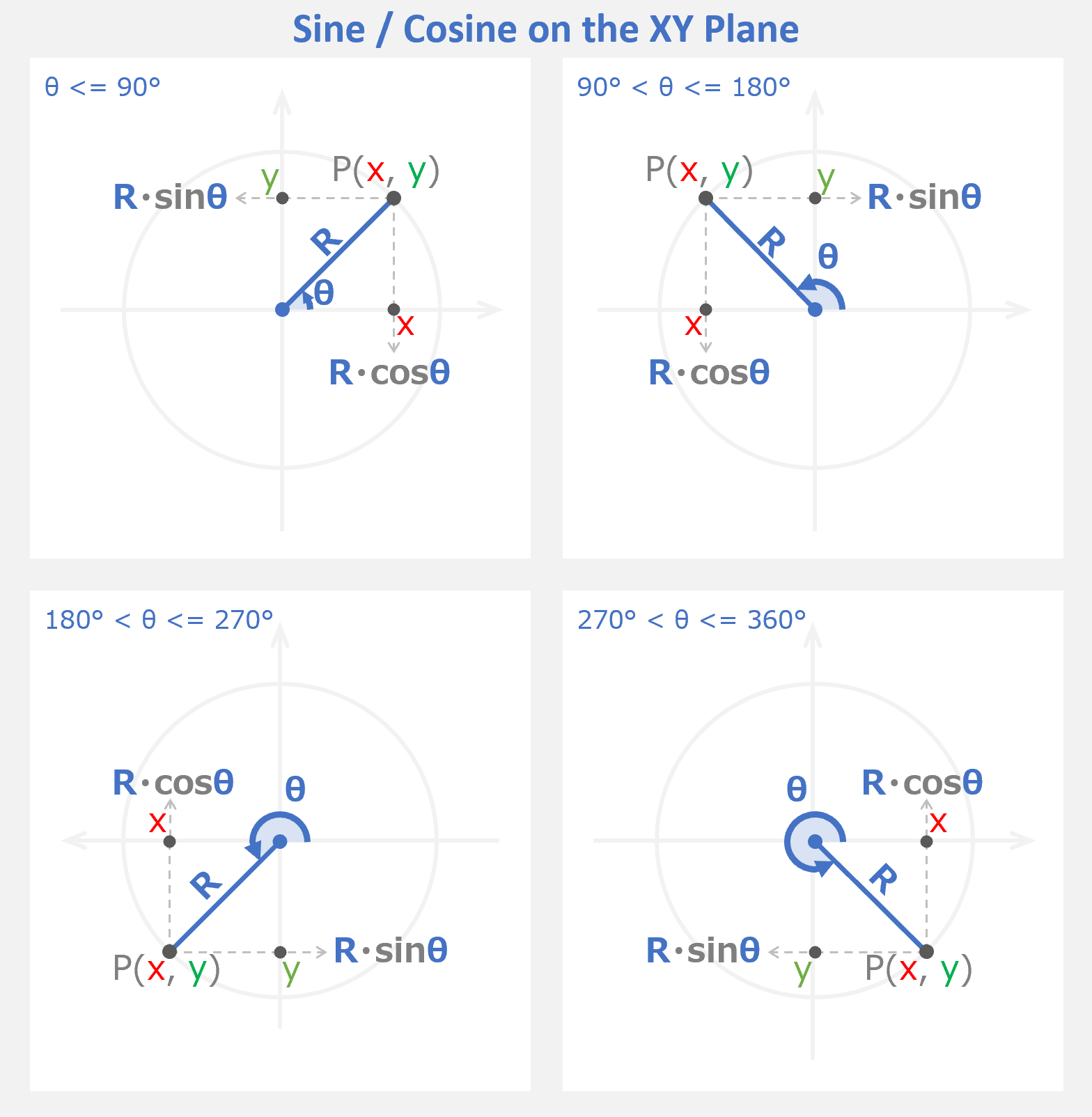
マスター「そして、サインとコサインに話を戻すと、、」
マスター「さっきの考え方を少し広げて、」
マスター「XY 平面上の原点 (0, 0) を中心とする」
パスター「半径 R の円を考えてみよう」
マスター「さっきのサインとコサインを応用すれば」
マスター「円周上の点 P の X 座標と Y 座標を」
マスター「求めることができるのがわかるか?」
パダワン「あっ! 直角三角形!!!」
パダワン「さっきの図と同じだ」
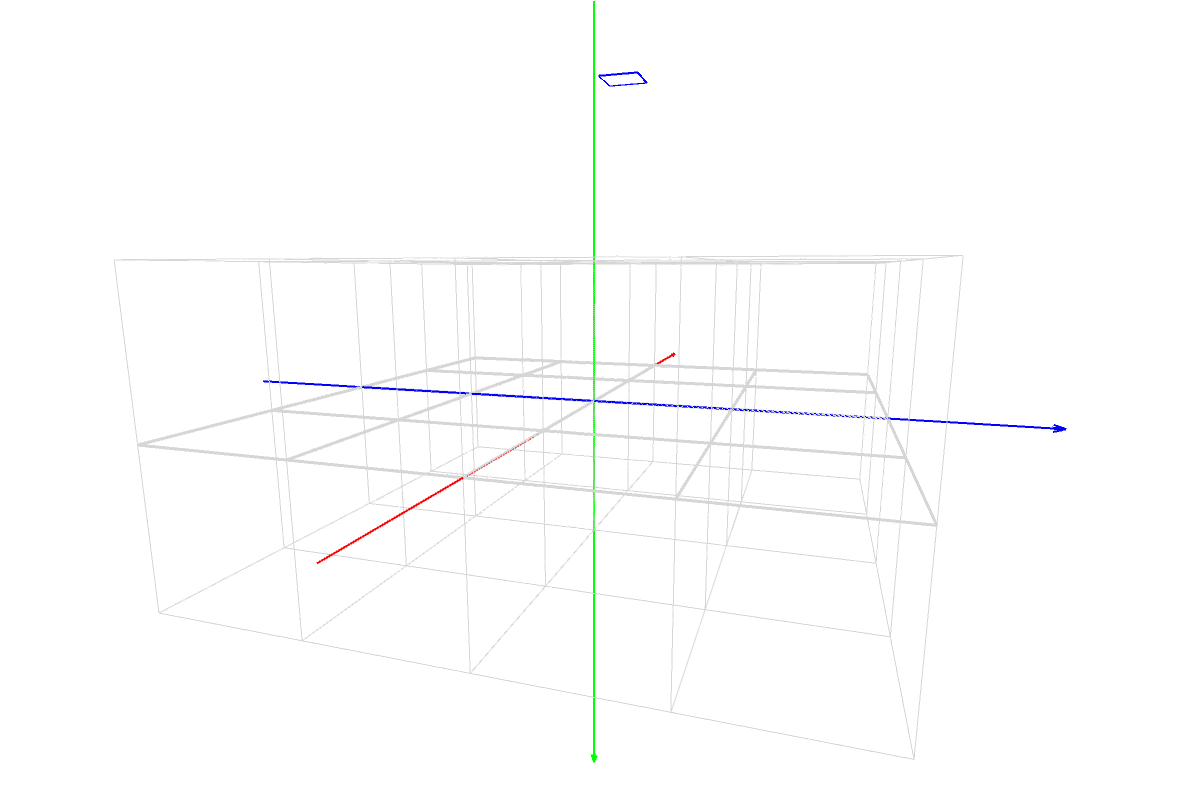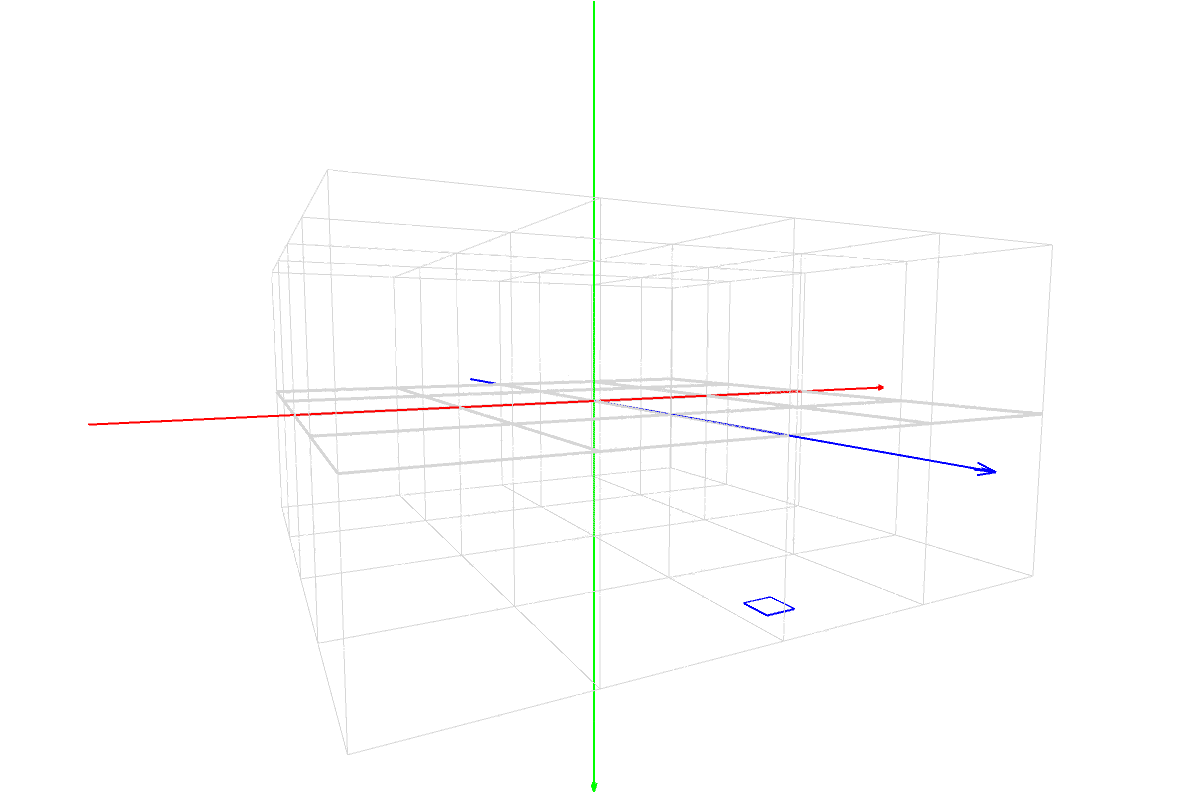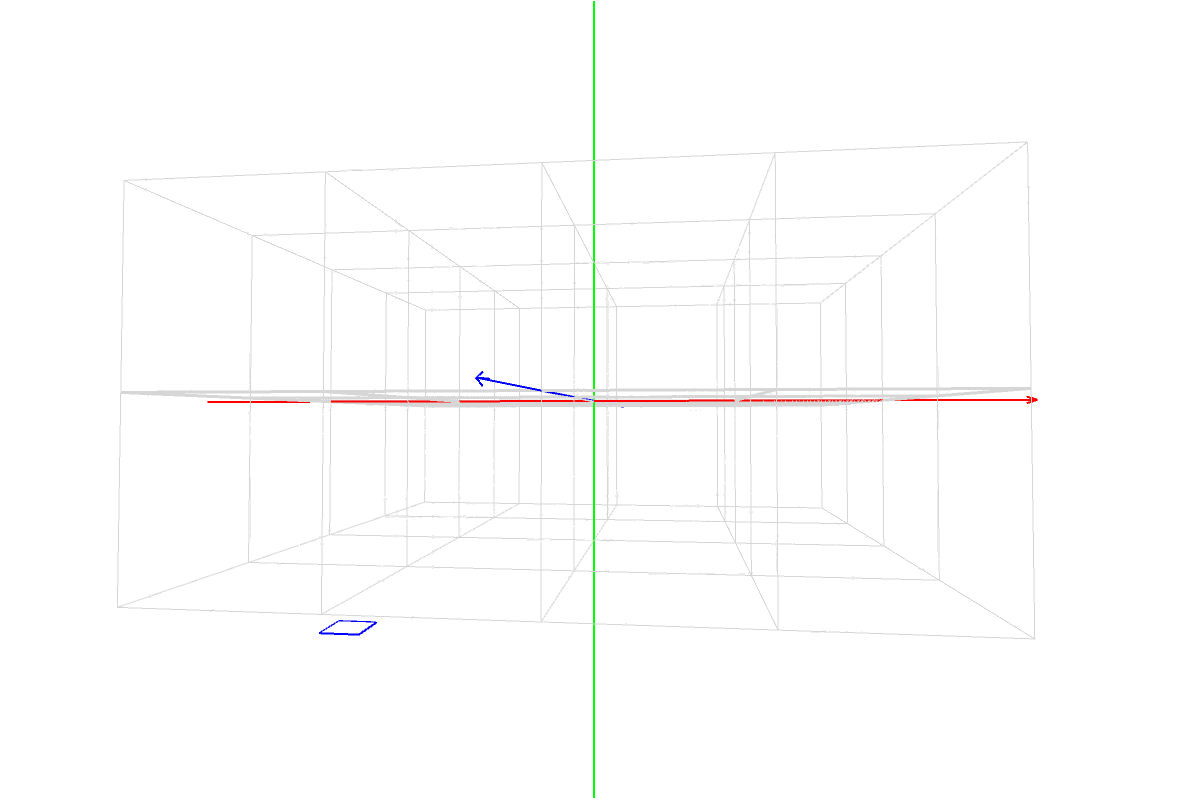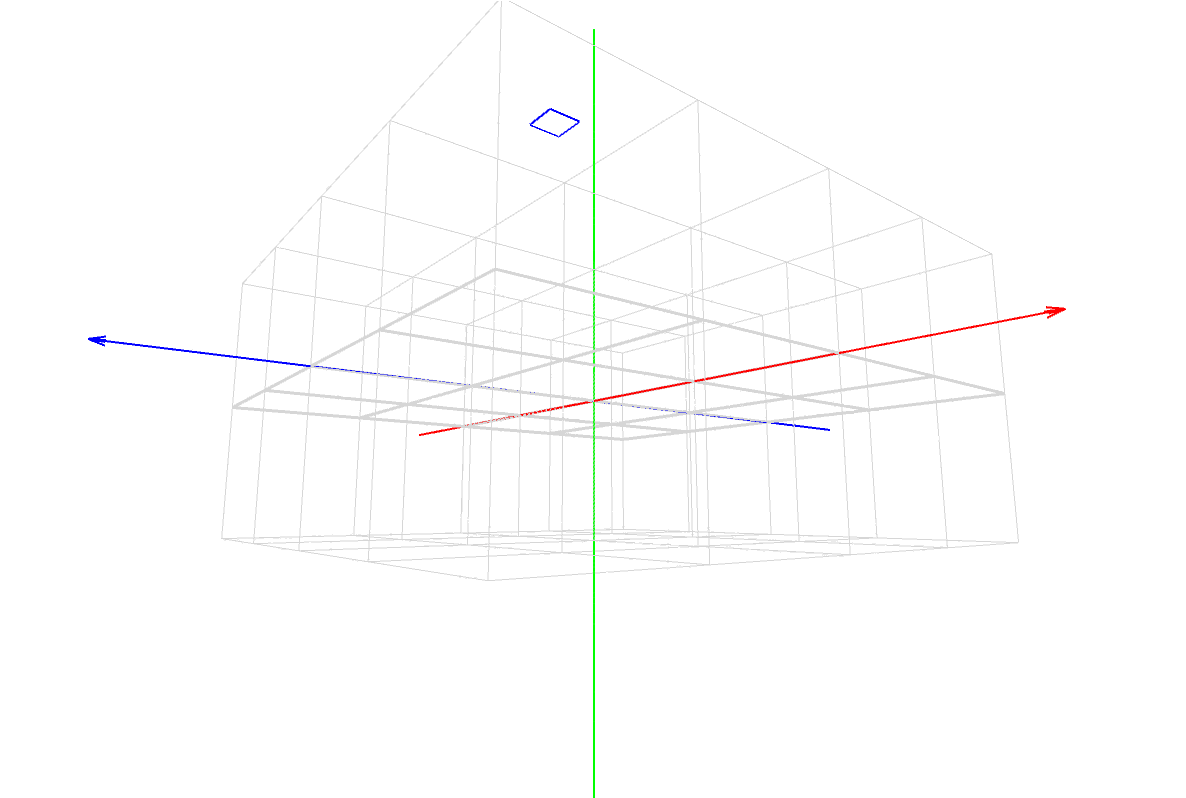
マスター「そうだ。そして、残りの 3 つの図が示しているように、」
マスター「これは、90°を超えても 180°を超えても 270°を超えても」
マスター「同じように求めることができるんだ」
パダワン「360°よりおっきくなったら?」
マスター「その場合も同じように求めることができるぞ!」
マスター「例えば、375°の場合は 15°の時と同じ結果になるんだ」
パダワン「あ、そっか! 360 引けば 15 になるもんね!」
マスター「ただし、、」
マスター「角度は 反時計回り であることに注意するんだぞ」
パダワン「逆回りはマイナス?」
マスター「そうだ。時計回りの場合はマイナスだ」
マスター「ここまで理解したら、、」
マスター「今は、円運動をするオブジェクトの、」
マスター「一定時間経過後の座標を知ろうとしているということを頭に入れて」
マスター「もう一度セーバーを見てみるんだ」
マスター「Y 軸が下向きであることも忘れるな」
マスター「下向きの場合は回転の正の向きは 時計回り になるぞ」
マスター「いいか、頭で考えず、体で空間を捉えるんだ!」
-
float dr = radians(dd);
セーバー起動時から一定時間後の角度 dd (degree: 度数法)を dr (radian: 弧度法) に変換している。 -
float x = R * cos(dr);
上で求めた角度 dr (ラジアン) の時の X 座標は cos(dr) に半径 R を乗じたものとなる。 -
float y = R * sin(dr);
同様に Y 座標は cos(dr) に半径 R を乗じたものだ。
パダワン「おお!わかってきた!!!」
パダワン「気がしないでもない …」
午前 0 時|3次元オブジェクトと座標変換
0 時 00 分|3次元オブジェクト (静止)
マスター「次は3次元オブジェクトだ」
マスター「以下を入力するんだ」
...
void draw() {
...
//updateObject4(); // <===== コメントアウト =====
updateObject5(); // <===== 追記 =====
}
...
// (5) 3次元オブジェクトの描画(静止) // <===== これ以降追記↓ =====
void updateObject5() {
noFill(); // 塗りつぶしなし
strokeWeight(2); // 枠線の太さ
stroke(255, 0, 255); // 枠線の色(R,G,B)
box(150);
}
マスター「説明する」
-
box(150);
これは 1 辺の長さが 150 の立方体(キューブ)を描いてるんだ。
パラメータを 3 つ渡せば、幅、高さ、奥行きを指定して、直方体にすることもできるぞ。
位置(座標)の指定はない。原点 (0,0,0) に描画されるんだ。
パダワン「おお!簡単すぎて泣けてくる」
パダワン「Vertex で頂点指定するよりずっと楽ちんじゃん!」
パダワン(これ先に教えてくれればよかったのに …)
パダワン(なんでマスタはいつも難しいのから始めるんだ?)

マスター「次は …」
マスター「以下の 2 行を追記するんだ」
// (5) 3次元オブジェクトの描画(静止)
void updateObject5() {
noFill(); // 塗りつぶしなし
strokeWeight(2); // 枠線の太さ
stroke(255, 0, 255); // 枠線の色(R,G,B)
box(150);
stroke(0, 255, 255); // 枠線の色(R,G,B) // <===== 追記 =====
sphere(60); // <===== 追記 =====
}
マスター「説明する」
-
sphere(60);
これは半径が 60 の球を描いてるんだ。
位置(座標)の指定はない。原点 (0,0,0) に描画されるんだ。
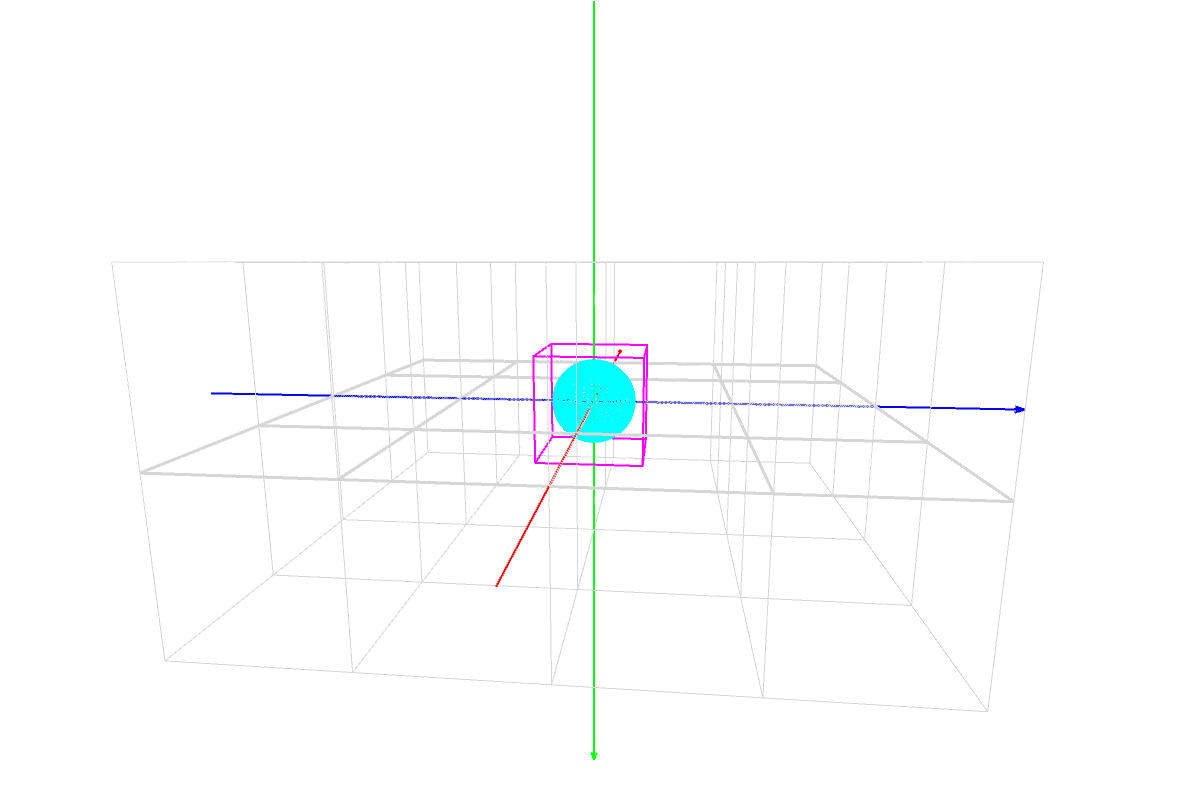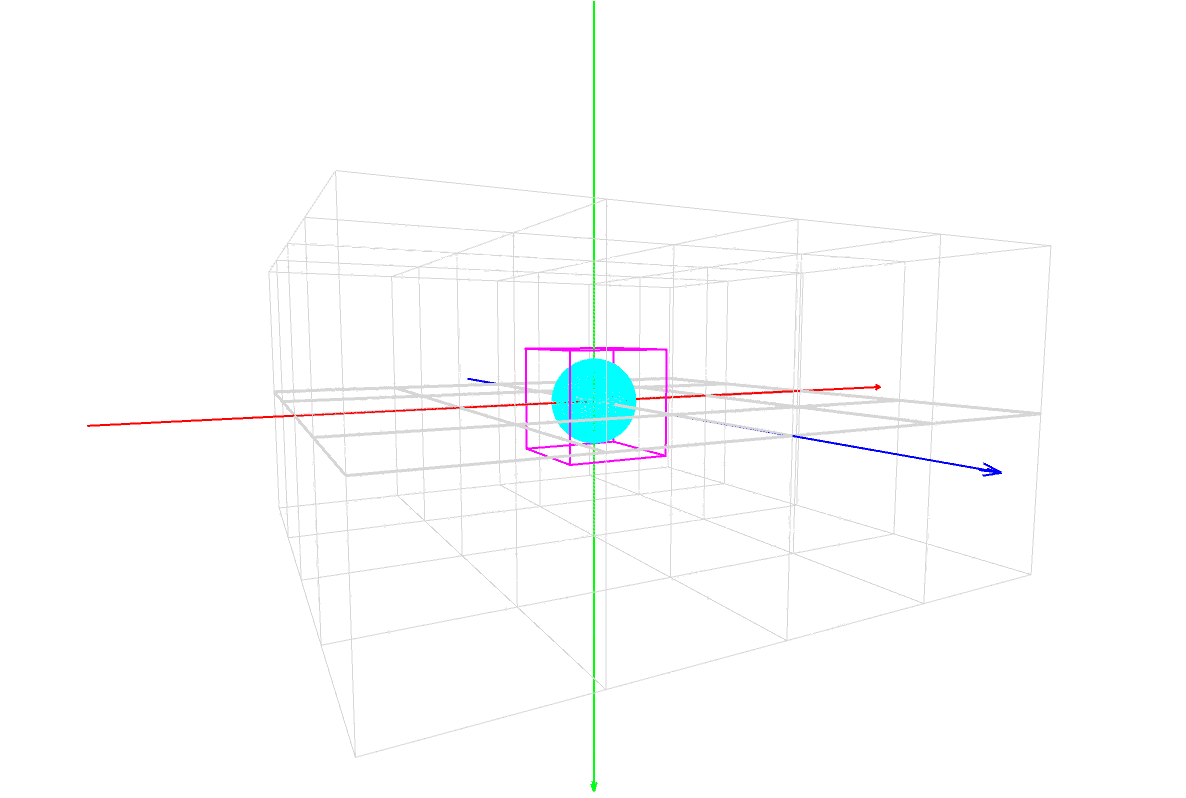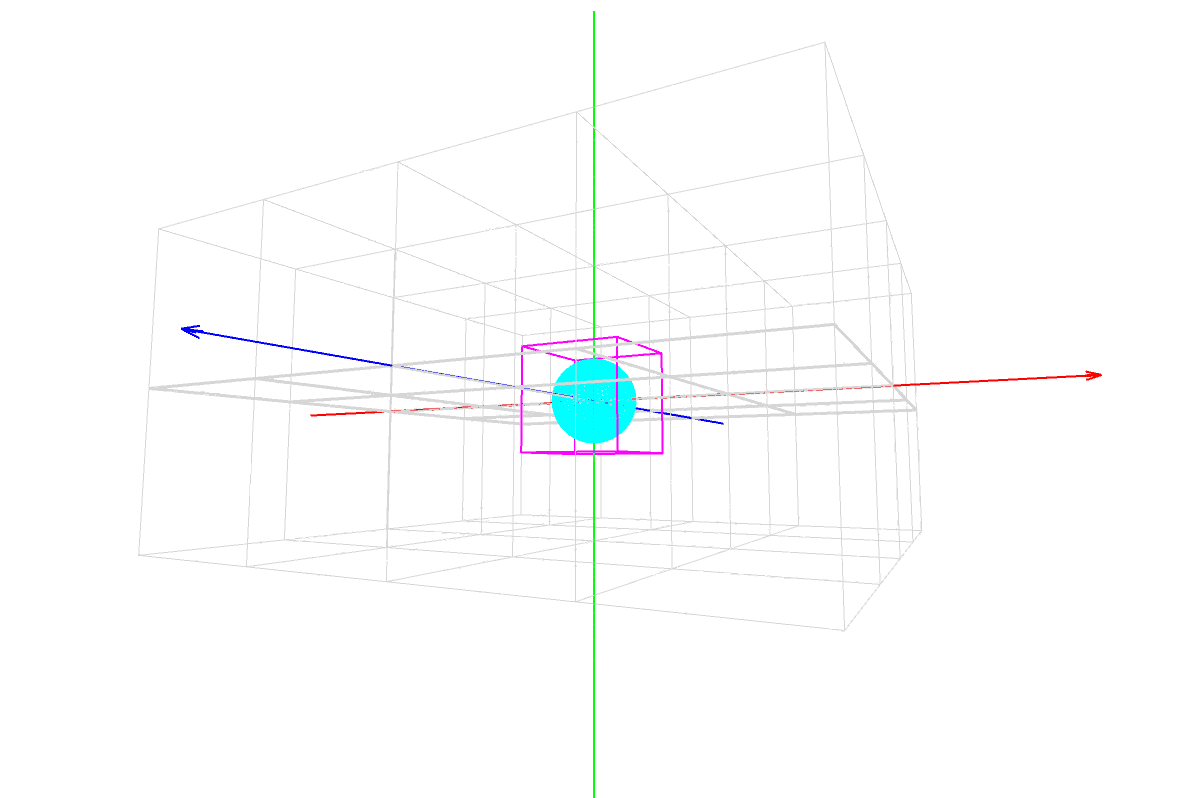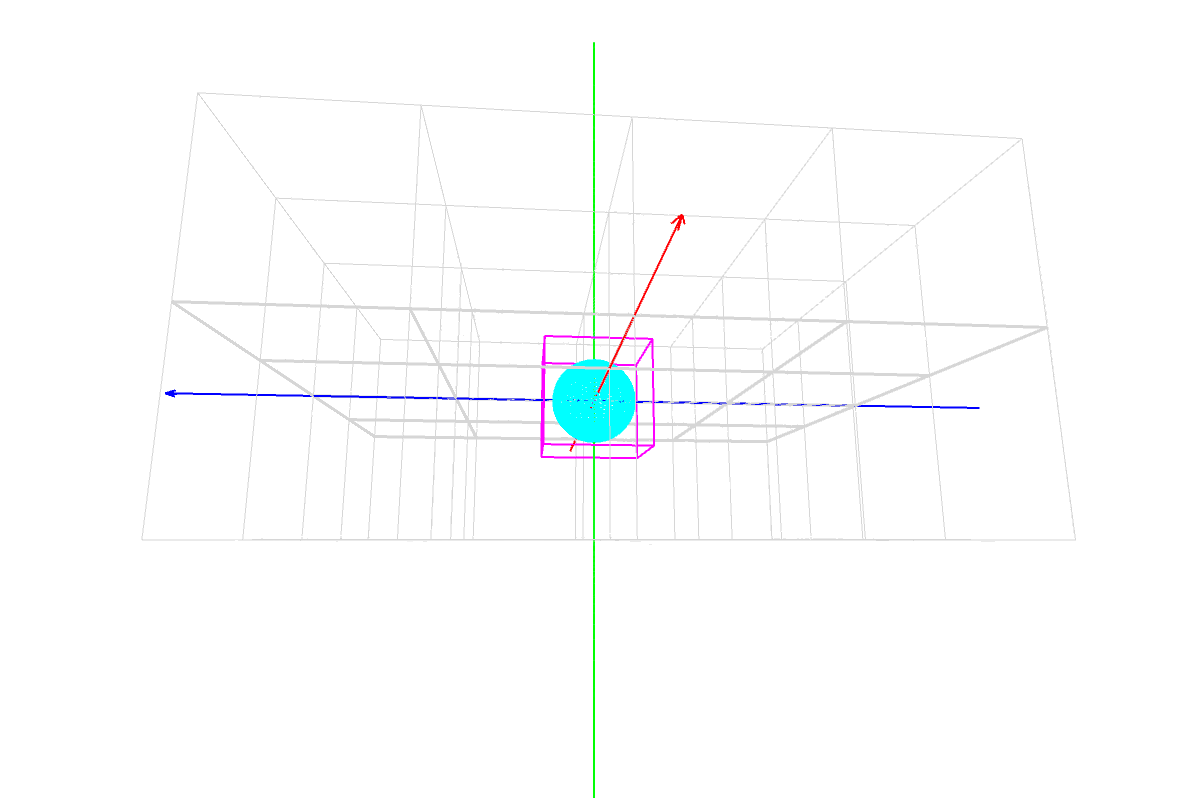
パダワン「あれれ??? noFill() で」
パダワン「塗りつぶし『なし』にしてんのに塗りつぶされてる …」
マスター「これは塗りつぶされているわけではない」
マスター「細かいメッシュで作られてるんだ」
マスター「setup() に setCameraOrbitalRadius(150); と追記してみるんだ」
void setup() {
size(1200, 800, P3D);
setCameraOrbitalRadius(150); // <===== 追記 =====
frameRate(24);
}
...
マスター「これは、DevUtils タブにコピペしたユーティリティの機能で」
マスター「カメラの公転軌道の半径を変えるものだ」
マスター「値を 150 に設定すると、原点 (0,0,0) にかなり近づくことができるぞ」

パダワン「あ、ほんとだ。ホネホネしてる」
マスター「見終わったらコメントアウトしておくのを忘れないように」
void setup() {
size(1200, 800, P3D);
//setCameraOrbitalRadius(150);
frameRate(24);
}
...
マスター「ついでに、ここでユーティリティの機能を説明しておくが、」
マスター「今は、ざっと見ておけばいい」
マスター「あとは、開発中にオブジェクトが見づらいとか、」
マスター「カメラがもっとゆっくり回るといいのにとか、」
マスター「キューブが邪魔だなとか」
マスター「逆にキューブの数増やしたいなとか思ったら」
マスター「その時に詳細を見ればいいだろう」
マスター「また、これは Processing の標準機能ではないから、」
マスター「その点だけ注意してくれ」
ユーティリティの説明
このユーティリティは本稿のために作成したもので、Processing での 3DCG 制作における開発初期の手間を省くことを目的としています。
開発ルーム(キューブや座標軸)を表示し、カメラを自動的に制御する機能を備えています。
メソッド一覧
| メソッド名 | 使う場所 | 概要 |
|---|---|---|
| setupDevRoom() | setup() | 開発ルームのセットアップ。キューブの大きさや数、カメラの諸条件などを設定する。 |
| setDevRoomAutoCameraEnabled() | setup() | カメラの自動制御をするかどうかを設定する。 |
| setDevRoomVisible() | setup() | キューブや座標軸を表示するかどうかを設定する。 なお、動作中に画面をクリックするとこのメソッドが呼び出され、表示のon/offをトグルできる。 |
| setCameraOrbitalRadius() | setup() | 原点(0,0,0)を中心に公転するカメラの軌道半径(ZX 平面)を設定する。 |
| setCameraMaxDepth() | setup() | カメラ位置の垂直方向(Y軸方向)の最大深さを設定する。 |
| setCameraOrbitalPeriod() | setup() | カメラの公転周期(秒数)を設定する。 |
| updateDevRoom() | draw() | 開発ルーム(キューブや座標軸)を描画する。 |
メソッド詳細
(1) void setupDevRoom(float len, int hnum, int vnum)
開発ルームのセットアップ(カメラの設定は自動調整)。
setup() メソッド内から呼び出されることを想定している。
このメソッドを呼び出さなかった場合はデフォルト値が使われる。
| パラメータ | デフォルト値 | 説明 |
|---|---|---|
| len | 200 | ルームに配置するキューブの一辺の長さ。 len==0 : キューブもフロアも座標軸も表示されない。 |
| hnum | 4 | キューブの水平方向(X,Z軸方向)の個数。 hnum<=0 : キューブは表示されないが、vnum>0 なら座標軸が表示される。 |
| vnum | 2 | キューブの垂直方向(Y 軸方向)の個数。 vnum<=0 : キューブは表示されないが、hnum>0 なら座標軸とフロアが表示される。 |
(2) void setupDevRoom(float len, int hnum, int vnum, float radius, float depth, int period)
開発ルームのセットアップ(カメラの設定含む)。
setup() メソッド内から呼び出されることを想定している。
このメソッドを呼び出さなかった場合はデフォルト値が使われる。
| パラメータ | デフォルト値 | 説明 |
|---|---|---|
| len | 200 | ルームに配置するキューブの一辺の長さ。 len==0 : キューブもフロアも座標軸も表示されない。 |
| hnum | 4 | キューブの水平方向(X,Z軸方向)の個数。 hnum<=0 : キューブは表示されないが、vnum>0 なら座標軸が表示される。 |
| vnum | 2 | キューブの垂直方向(Y 軸方向)の個数。 vnum<=0 : キューブは表示されないが、hnum>0 なら座標軸とフロアが表示される。 |
| radius | ルーム横幅の1.25倍 | 原点(0,0,0)を中心に公転するカメラの軌道半径(ZX 平面)。 radius==0.0 : radius==0.1 と同じ。 radius< 0.0 : 動作不定。おそらくabs(radius)と同じ。 |
| depth | ルーム高さの半分 | カメラ位置の垂直方向(Y軸方向)の最大深さ。 -depth ~ +depth の範囲を動く depth==0.0 : 上下動(Y軸方向の移動)なし。 depth< 0.0 : 上下の向きが逆になる(位相が半周分ずれる)。 |
| period | 16秒 | カメラの公転周期(秒)。 period==0 : period==1 と同じ。 period< 0 : カメラの公転方向が逆向きになる |
(3) void setDevRoomAutoCameraEnabled(boolean isEnabled)
カメラの自動制御をするかどうかを指定する。
setup() メソッド内から呼び出されることを想定している。
| パラメータ | デフォルト値 | 説明 |
|---|---|---|
| isEnabled | true | true: カメラを自動制御する。 false: カメラを自動制御しない。 |
(4) void setDevRoomVisible(boolean isVisible)
開発ルーム(キューブや座標軸など)を表示するかどうかを指定する。
setup() メソッド内から呼び出されることを想定しているが、draw() 内で呼び出しても良い。
| パラメータ | デフォルト値 | 説明 |
|---|---|---|
| isVisible | true | true: 開発ルームを表示する。 false: 開発ルームを表示しない。 |
(5) void setCameraOrbitalRadius(float radius)
原点(0,0,0)を中心に公転するカメラの軌道半径(ZX 平面)を設定する。
setup() メソッド内から呼び出されることを想定している。
| パラメータ | デフォルト値 | 説明 |
|---|---|---|
| radius | ルーム横幅の1.25倍 | 原点(0,0,0)を中心に公転するカメラの軌道半径(ZX 平面)。 radius==0.0 : radius==0.1 と同じ。 radius< 0.0 : 動作不定。おそらくabs(radius)と同じ。 |
(6) void setCameraMaxDepth(float depth)
カメラ位置の垂直方向(Y軸方向)の最大深さを設定する。
setup() メソッド内から呼び出されることを想定している。
| パラメータ | デフォルト値 | 説明 |
|---|---|---|
| depth | ルーム高さの半分 | カメラ位置の垂直方向(Y軸方向)の最大深さ。 -depth ~ +depth の範囲を動く depth==0.0 : 上下動(Y軸方向の移動)なし。 depth< 0.0 : 上下動の向きが逆になる(位相が半周分ずれる)。 |
(7) void setCameraOrbitalPeriod(int period)
カメラの公転周期を設定する。
setup() メソッド内から呼び出されることを想定している。
| パラメータ | デフォルト値 | 説明 |
|---|---|---|
| period | 16秒 | カメラの公転周期(秒)。 period==0 : period==1 と同じ。 period< 0 : カメラの公転方向が逆向きになる |
(8) void updateDevRoom()
開発ルームを更新する。
カメラの位置を更新し、開発ルームを描画する。
draw() メソッド内から呼び出されることを想定している。
0 時 20 分~|等速直線運動
パダワン「3D オブジェクト、簡単すぎて笑いがでちゃうけど、、」
パダワン「でもさぁ …」
パダワン「位置が指定できないってことは、」
パダワン「動かせないってことぉ???」
パダワン「なんかダサすぎて哀しい …」
マスター「がはは!ちゃんと動かせるから心配するな」
パダワン「え?ほんとぉ?!」
マスター「次のように入力するんだ!」
...
void draw() {
...
//updateObject5(); // <===== コメントアウト =====
updateObject6(); // <===== 追記 =====
}
...
// (6) 3次元オブジェクト(座標変換で等速直線運動) // <===== これ以降追記↓ =====
// (3) と似た動きを座標変換で実現
void drawEarth() {
fill(224, 224, 255); // 塗りつぶし色(R,G,B)
stroke(0, 0, 255); // 枠線の色(R,G,B)
strokeWeight(2); // 枠線の太さ
box(80);
}
void updateObject6() {
final float START = -600; // 開始時点の位置
final float SPEED = 200; // 秒速
float ms = millis(); // プログラム開始時点からの経過ミリ秒
float d = ms * SPEED / 1000; // 移動距離
float p = START + d; // 現在位置
pushMatrix();
translate(p, -100, 50);
drawEarth();
popMatrix();
}
マスター「説明する」
-
void drawEarth() {...}
まずはオブジェクトの描画をこのメソッドに切り分ける。
今回は地球と見立てて、drawEarth() という名前にする。
メソッドの中で呼び出しているfill()、stroke()、strokeWeight()、box(80)はこれまで習ったとおりだ。 -
void updateObject6() {...}- 定数
START、SPEED、変数ms、d、pもさっき書いた等速直線運動とほぼ同じだ。 -
pushMatrix();
現在のマトリクスをスタックにプッシュして、座標変換の開始を宣言する。 -
translate(p, -100, 50);
現在の座標 (0, 0, 0) から、(p,-100,50) の位置まで並行移動する。
X 座標のみ変数 p を指定し、あとは定数リテラルを指定しているから、時間経過とともに X 座標のみが変化する、つまり X 軸と並行に移動しているのがわかるだろう。 -
drawEarth();
地球に見立てたオブジェクトを描画する。 -
popMatrix();
現在のマトリクスをスタックからポップして、座標変換の終了を宣言する。
- 定数

パダワン「おお!動いた!動いた!」
パダワン「地球って青くて四角い星なんだね?!」
マスター「…」
ローカル座標系
パダワン「でもさぁ」
パダワン「translate() -> drawEarth() の順番ってことは、、」
パダワン「えーと …」
パダワン「動かすときは、描いたやつがないのに、、」
パダワン「なんで描いたやつが動くの???」
マスター「いいところに気づいたな!」
マスター「それでは translate() についてもう少し詳しく説明しよう」
マスター「これは、描いたものを動かしているのではなく、、」
マスター「描く『舞台』を動かしているのだ」
パダワン「へ???」
マスター「分かりやすく、ZX 平面だけで考えてみよう」
マスター「次の図を見るんだ!」

マスター「これまではワールド座標系に直接描いてきたが、、」
マスター「実はローカル座標系というものがあるんだ」
マスター「まあ、あるオブジェクト専用の座標系だと思えばいい」
マスター「図の左側は、これまで描いてきた世界だ」
マスター「2 つの座標軸が重なっているだろう?」
マスター「大きい方がワールド座標系で、小さい方がローカル座標系だ」
マスター「そして、、」
マスター「図の右側が、今回描いている世界だ」
パダワン「あ!バッテンがずれてる …」
マスター「そうだ」
マスター「それをずらしているのが translate() なんだ」
マスター「つまり translate() によって」
マスター「ローカル座標系が平行移動しているということだ」
マスター「そして、オブジェクトの描画はローカル座標系に対して行われるんだ」
パダワン「ほんとだ」
パダワン「小っちゃいバッテンだけ見ると、右も左も」
パダワン「vertex() で描いた四角が同じとこにある」
マスター「そして、さっきはローカル座標系が」
マスター「あるオブジェクト専用の座標系と言ったが、」
マスター「例えば、 translate() した後に、3つのオブジェクトを描画したら」
マスター「3 つのオブジェクトはすべて同じローカル座標系が使われるんだ」
マスター「また、translate() を 2 回続けて実行すると」
マスター「最初の translate() でローカル座標系が移動し、」
マスター「2 回目の呼び出しでは、」
マスター「1 度めに移動した場所から更に移動することになるんだ」
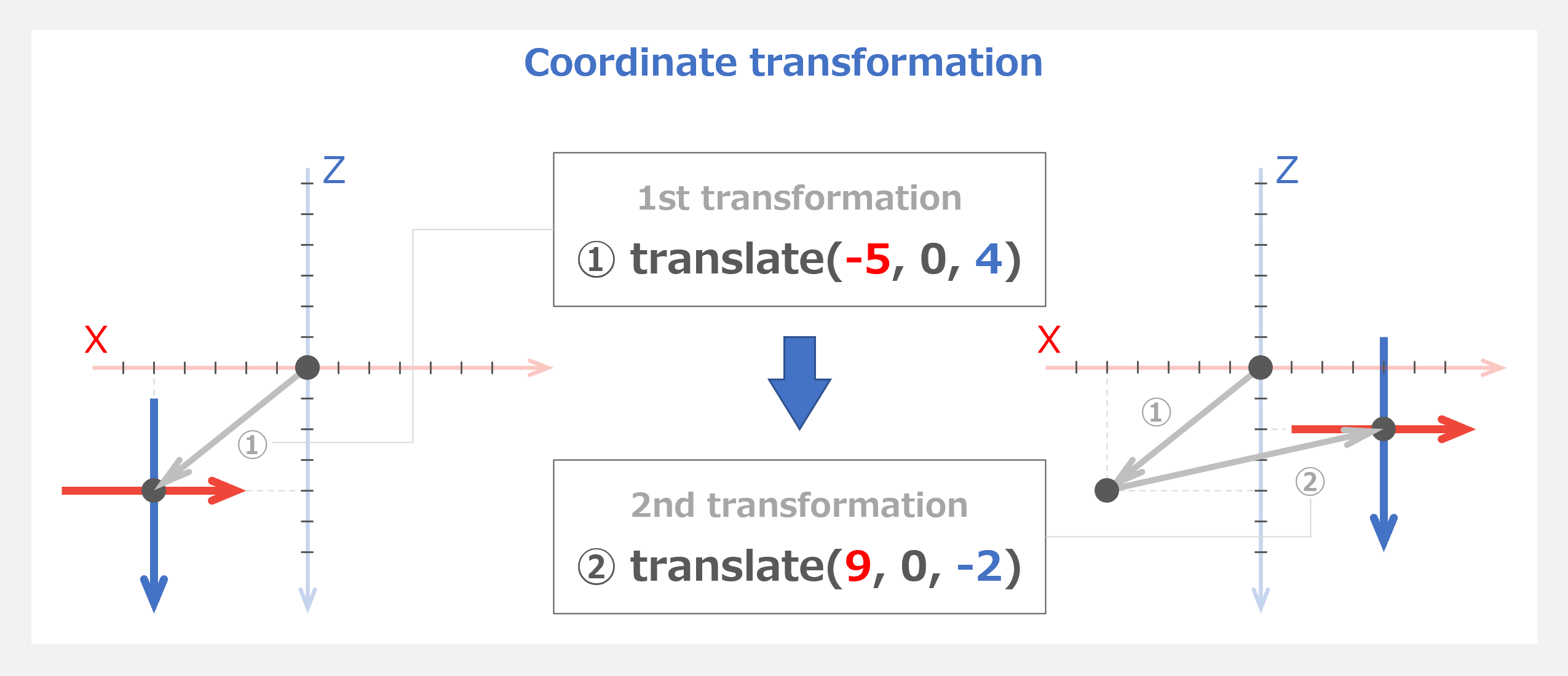
マスター「だから、描画する舞台の開始と終了を宣言する必要があり、」
マスター「それを担うのが pushMatrix() と popMatrix() だ」
マトリクスとスタック
マスター「Matrix というのは、ひとまずローカル座標系とワールド座標系の」
マスター「関係を示す『現在の状態』だと思っておけばいい」
マスター「そしてそれはセーバーの中に 1 つしか存在せず」
マスター「その 1 つをセーバー内のいろんなところから共有して使ってるんだ」
マスター「だから、たとえばあるメソッドが」
マスター「自分が描画するために Matrix を変更したら」
マスター「それを使い終わった後で元に戻しておいてやらないと」
マスター「次のメソッドが困ってしまうんだ」
マスター「でも、毎回毎回」
マスター「translate(5, 0, 10) の後で translate(-5, 0, -10)」
マスター「などと書いて戻していたら大変だろう?」
マスター「だから Processing では、現在の Matrix の状態を」
マスター「スタックに退避させる機能が備わっているんだ」
マスター「スタックは習ったな?」
パダワン「うん。先入れ後出し!」
パダワン「皿洗いのやつ!!!」
マスター「そうだ。つまり、、」
マスター「pushMatrix() は現在の Matrix をスタックに退避し、」
マスター「popMatrix() は最後に退避した Matrix をスタックから取り出して」
マスター「現在の Matrix に復帰させるんだ」
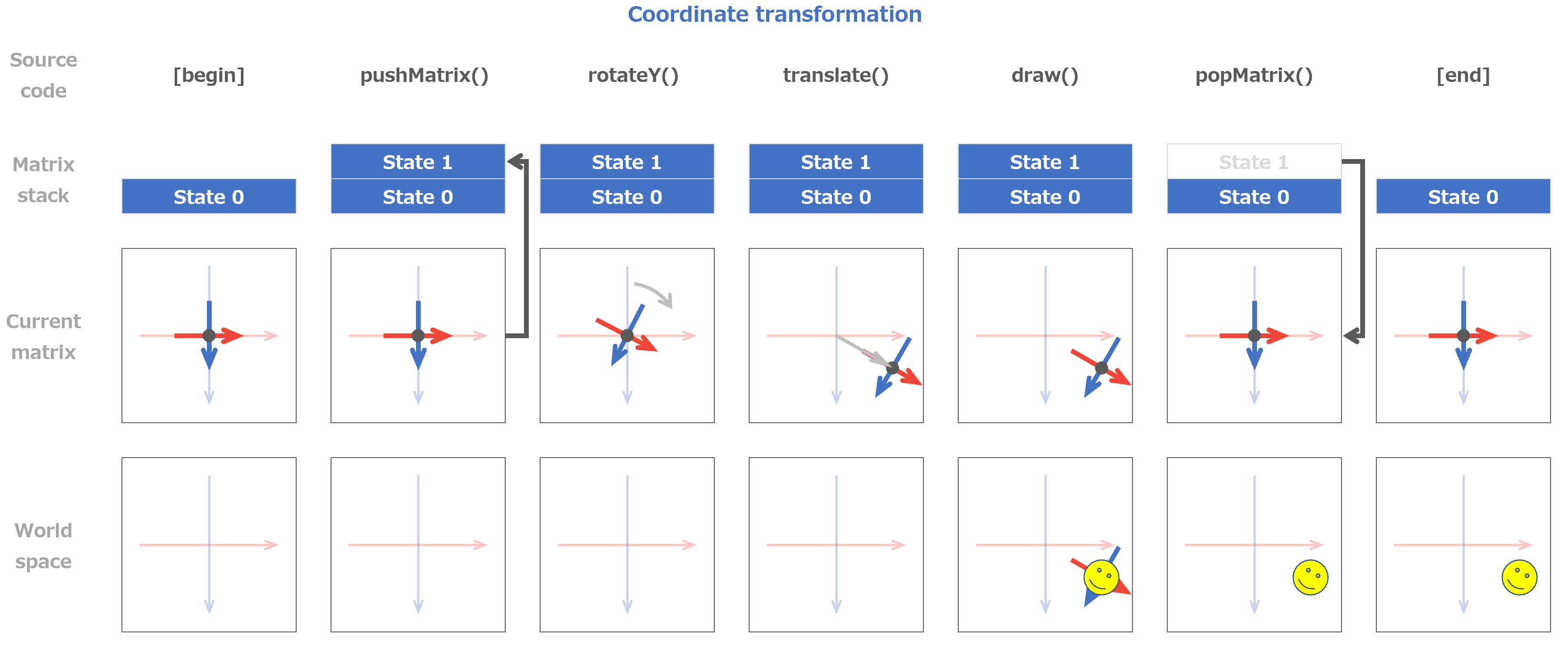
マスター「次の図は、座標変換と描画を行った際に、」
マスター「スタックや Matrix の状態がどのように変化するかを表したものだ」
マスター「分かりやすくするために ZX 平面だけを対象にしており、」
マスター「時系列は左から右へ流れている」
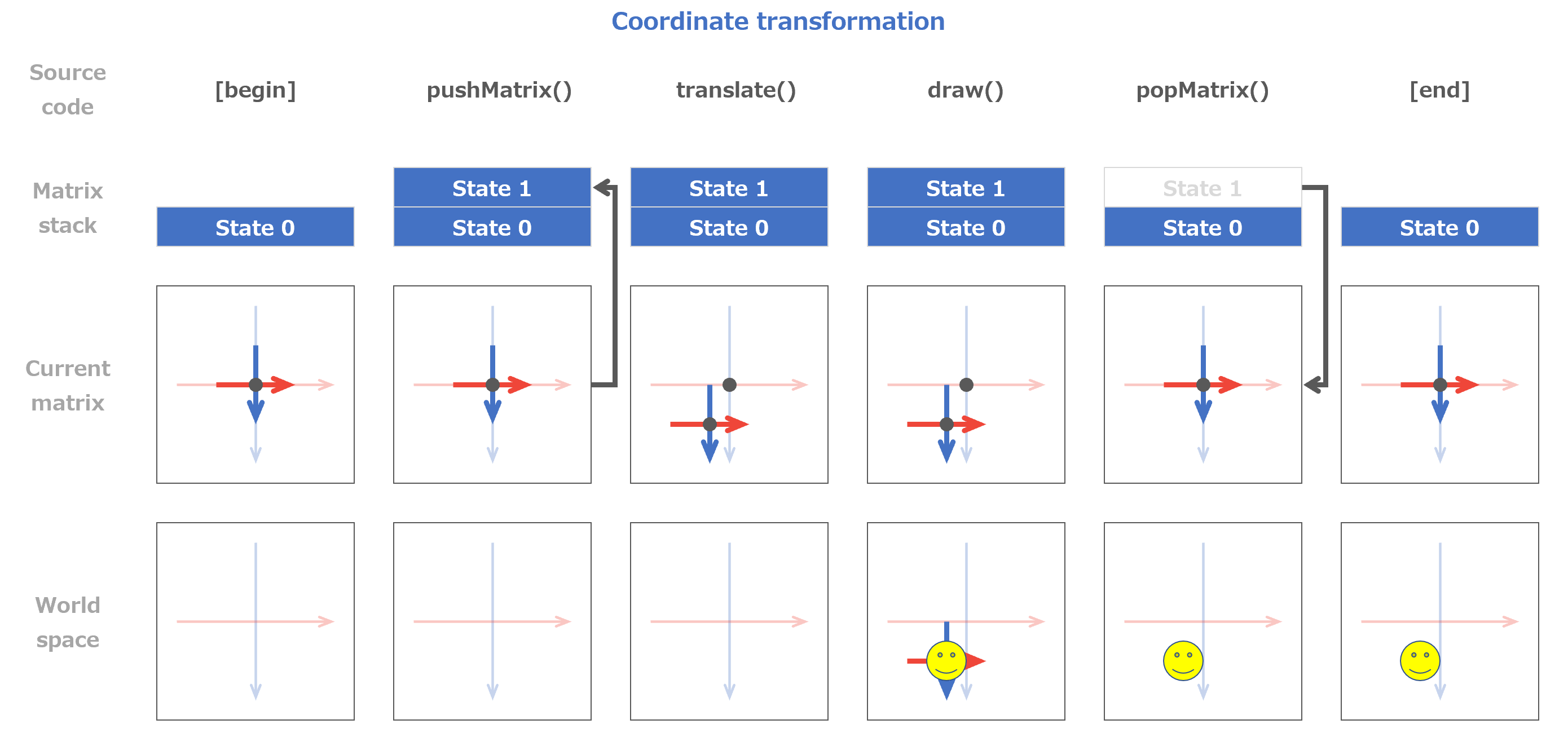
マスター「このイメージを頭に叩き込むんだ」
0 時 40 分|自転
マスター「次のように入力するんだ!」
...
void draw() {
...
//updateObject6(); // <===== コメントアウト =====
updateObject7(); // <===== 追記 =====
}
...
// (7) 3次元オブジェクト(座標変換で自転) // <===== これ以降追記↓ =====
void updateObject7() {
final float SPEED = 60; // 角度(Degree)/秒
float ms = millis(); // プログラム開始時点からの経過ミリ秒
float dd = ms * SPEED / 1000; // 移動角度(Degree)
float dr = radians(dd); // 移動角度(Radian)
pushMatrix();
rotateY(dr);
drawEarth();
popMatrix();
}
マスター「説明する」
-
final float SPEED = 60;
これはオブジェクトを自転させるプログラムなのだが、1秒間に動く角度をここで指定している。 -
float dd = ms * SPEED / 1000;
セーバー起動時点から動いた角度 (度数) だ。 -
float dr = radians(dd);
セーバー起動時点から動いた角度をラジアンに直したものだ。 -
pushMatrix();
さっき教えた通り、現在のマトリクスを退避している。 -
rotateY(dr);
Y 軸を中心にして(ZX 平面に沿って)、ローカル座標系を角度 dr だけ回転させている。rotateY()の他にroateX()、rotateZ()もあるぞ。 -
drawEarth();
ひとつ前に作った drawEarth() を呼び出している。座標変換を使えば、このようにオブジェクトを何度も使いまわせるようになるんだ。 -
popMatrix();
さっき教えた通り、現在のマトリクスを復帰させている。
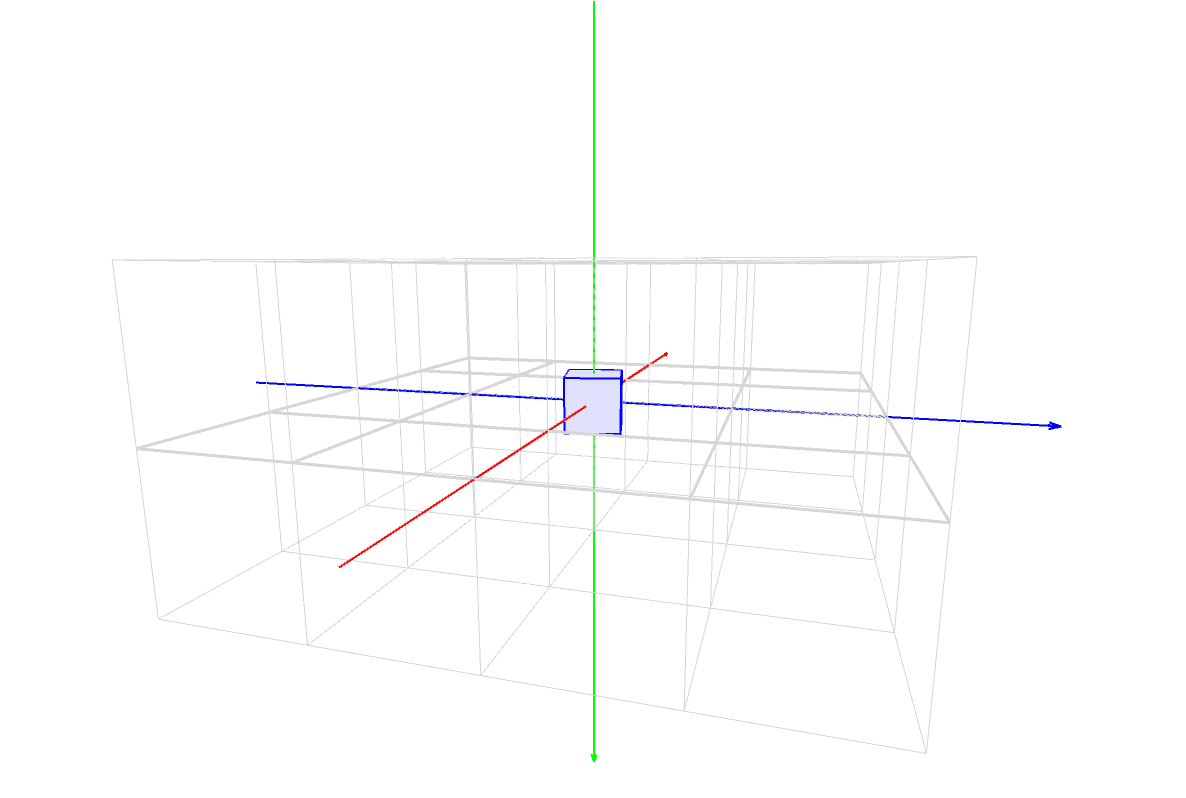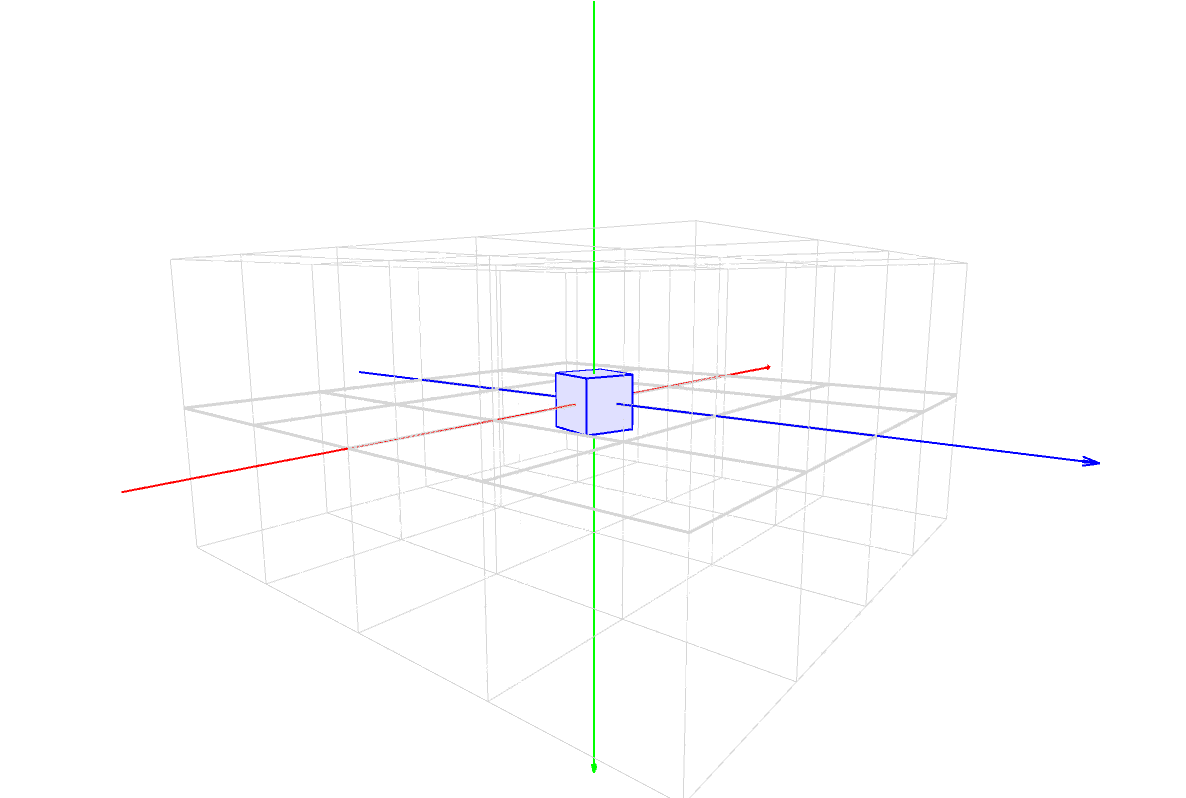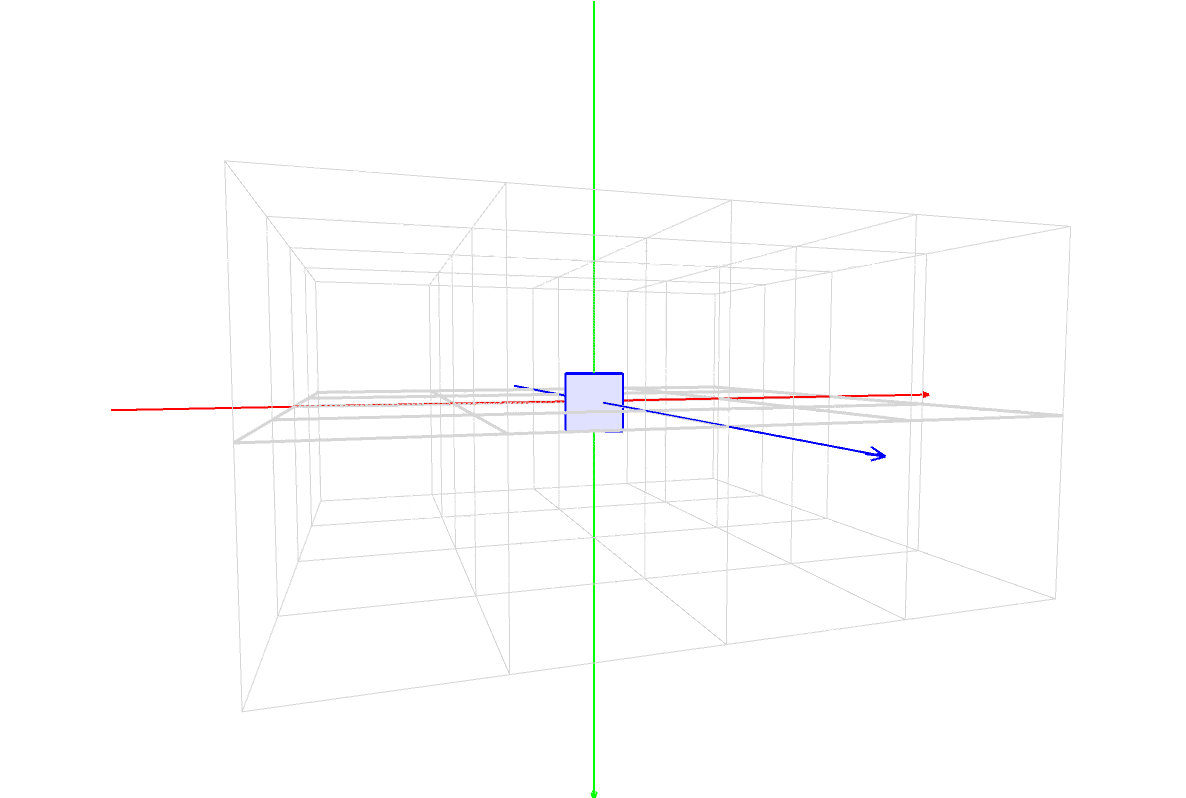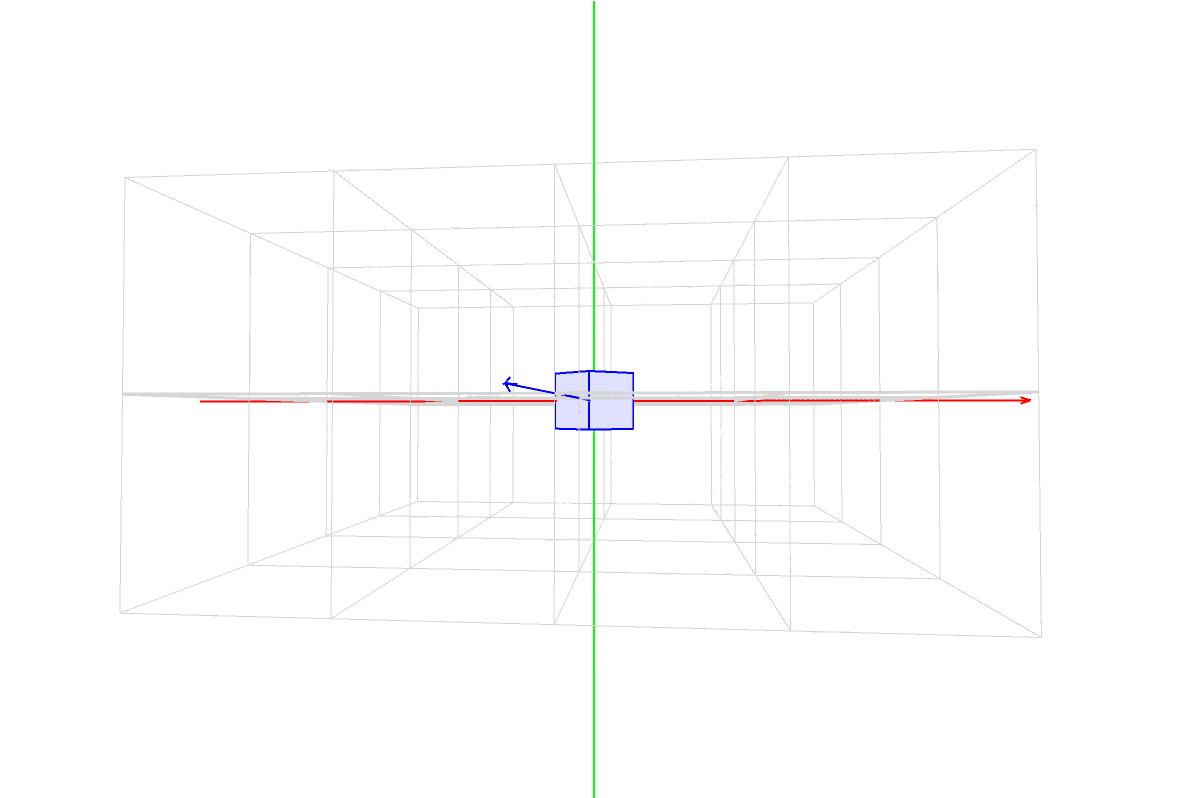
パダワン「ん???」
パダワン「回してんのに、、」
パダワン「三角関数使わなくていいの?」
マスター「ああ、不要だ」
パダワン「げっ!、こんなに楽ちんなのがあるのか!!!」
パダワン(これ先に教えてくれればよかったのに …)
パダワン(なんでマスタはいつも難しいのから始めるんだ?)
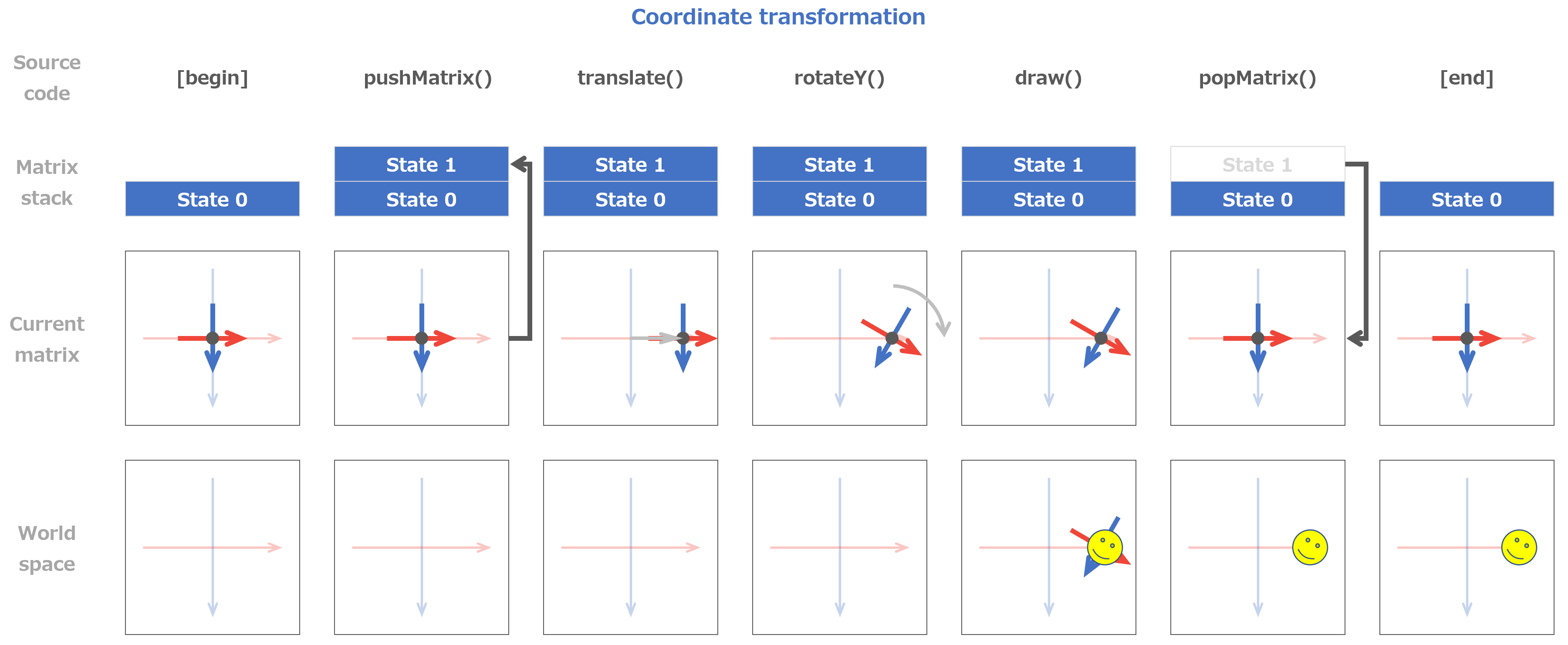
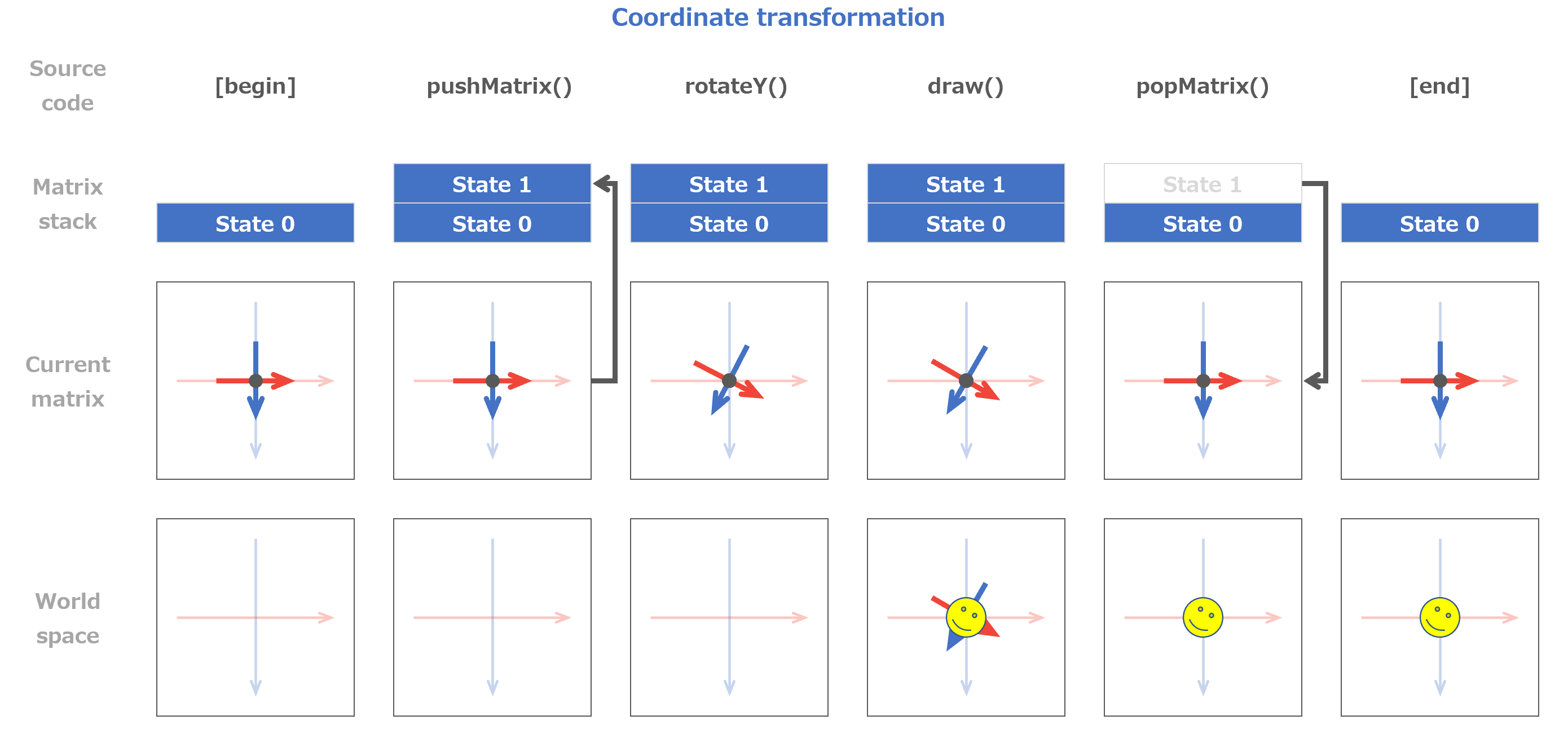
マスター「なお、スタックやマトリクスの状態遷移は次のとおりだ」
午前 1 時|変換を組み合わせる
1 時 00 分|公転(等速円運動)
マスター「平行移動と回転を組み合わせた変換を試してみよう」
マスター「次のように入力するんだ!」
...
void draw() {
...
//updateObject7(); // <===== コメントアウト =====
updateObject8(); // <===== 追記 =====
}
...
// (8) 3次元オブジェクト(座標変換で公転) // <===== これ以降追記↓ =====
// (4) と似た動きを座標変換で実現
void updateObject8() {
final float R = 300; // 公転半径
final float SPEED = 150; // 角度(Degree)/秒
float ms = millis(); // プログラム開始時点からの経過ミリ秒
float dd = ms * SPEED / 1000; // 移動角度(Degree)
float dr = radians(dd); // 移動角度(Radian)
pushMatrix();
rotateY(dr);
translate(R, 0, 0);
drawEarth();
popMatrix();
}
マスター「説明する」
-
final float R = 300;
このセーバーは、ワールド座標系の原点 (0,0,0) を中心にオブジェクトを公転させるものだが、この R はその公転軌道の半径だ。 -
SPEEDmsdddr
説明はもう不要だろう。dr はセーバー起動時点からの回転角度だ。 -
pushMatrix()roateY(dr)drawEarth()popMatrix()
これもさっきと同じだ。 -
translate(R, 0, 0);
さっきと違うのはこれだ。rotateY(dr) の後に X 軸方向に半径 R 分だけ平行移動をさせている。
1 時 20 分|離れた位置で自転
マスター「そうしたら、今後は変換の順序を変えてみる」
マスター「次のように入力するんだ!」
...
void draw() {
...
//updateObject8(); // <===== コメントアウト =====
updateObject9(); // <===== 追記 =====
}
...
// (9) 3次元オブジェクト(座標変換で離れた位置で自転) // <===== これ以降追記↓ =====
// (8) との違いに注目
void updateObject9() {
final float R = 300; // 公転半径
final float SPEED = 150; // 角度(Degree)/秒
float ms = millis(); // プログラム開始時点からの経過ミリ秒
float dd = ms * SPEED / 1000; // 移動角度(Degree)
float dr = radians(dd); // 移動角度(Radian)
pushMatrix();
translate(R, 0, 0); // 順序を入れ替えただけ
rotateY(dr); // 順序を入れ替えただけ
drawEarth();
popMatrix();
}
マスター「これは説明するまでもない」
マスター「さっきとは、rotateY() と translate() の順序を変えただけだ」
パダワン「お、止まったまま、回ってる …」

マスター「カメラも回転しているから、自転の動きがよくわからないかもしれない」
マスター「その場合は、ユーティリティの関数 setCameraOrbitalPeriod() を使って」
マスター「カメラの公転周期を長くすると良いだろう」
...
void setup() {
size(1200, 800, P3D);
//setCameraOrbitalRadius(150);
setCameraOrbitalPeriod(120); // <===== 追記 =====
frameRate(24);
}
...
マスター「見終わったらコメントアウトしておくのを忘れないように」
...
void setup() {
size(1200, 800, P3D);
//setCameraOrbitalRadius(150);
//setCameraOrbitalPeriod(120);
frameRate(24);
}
...
マスター「座標変換の順序で挙動が大きく変わるから注意するんだ」
1 時 40 分|公転体の周りを公転
マスター「そうしたら、今度は太陽、地球、月に見立てたオブジェクトを動かすぞ」
マスター「次のように入力するんだ!」
...
void draw() {
...
//updateObject9(); // <===== コメントアウト =====
updateObject10(); // <===== 追記 =====
}
...
// (10) 3次元オブジェクト(座標変換で公転体の周りを公転) // <===== これ以降追記↓ =====
void drawSun() {
noFill(); // 塗りつぶしなし
stroke(255, 0, 0); // 枠線の色(R,G,B)
strokeWeight(2); // 枠線の太さ
sphere(60);
}
void drawMoon() {
fill(255, 255, 128); // 塗りつぶし色(R,G,B)
stroke(255, 0, 0); // 枠線の色(R,G,B)
strokeWeight(2); // 枠線の太さ
beginShape();
vertex(-20, -20, 0);
vertex( 20, -20, 0);
vertex( 20, 20, 0);
vertex(-20, 20, 0);
endShape(CLOSE);
}
void updateObject10() {
float ms = millis(); // プログラム開始時点からの経過ミリ秒
final float E_R = 400; // 地球の公転半径
final float E_SPEED = 80; // 地球の角度(Degree)/秒
float edd = ms * E_SPEED / 1000; // 地球の移動角度(Degree)
float edr = radians(edd); // 地球の移動角度(Radian)
final float M_R = 100; // 月の公転半径
final float M_SPEED = 200; // 月の角度(Degree)/秒
float mdd = ms * M_SPEED / 1000; // 月の移動角度(Degree)
float mdr = radians(mdd); // 月の移動角度(Radian)
drawSun();
pushMatrix();
{
rotateY(edr);
translate(E_R, 0, 0);
drawEarth();
pushMatrix();
{
rotateY(mdr);
translate(M_R, 0, 0);
drawMoon();
}
popMatrix();
}
popMatrix();
}
マスター「説明する」
- void drawSun() {...}
- これはさっき作った地球オブジェクトを描く drawEarth() と同じように、太陽を模したオブジェクトを描くものだ。太陽は「球」にしている。
- void drawMoon() {...}
- 同様に、月を模したオブジェクトを描くメソッドだ。月は二次元オブジェクトの矩形としている。
- void updateObject10() {...}
-
E_RE_SPEEDeddedr
これは地球の公転半径や公転速度を定めたものだ。
これまで何度も書いたものなので詳細の説明は必要ないだろう。 -
M_RM_SPEEDmddmdr
これは月の公転半径や公転速度を定めたものだ。
これも説明は不要なはずだ。 - ここからが本題だ。
-
drawSun();『太陽』をワールド座標系に直接描画。 -
pushMatrix();『地球』の描画用に現在のマトリクスを退避。 -
{
-
rotateY(edr);ローカル座標系を回転。 -
translate(E_R, 0, 0);ローカル座標系を外側に移動。 -
drawEarth();『地球』を描画。 -
pushMatrix();『月』の描画用にマトリクスを退避。 -
{-
rotateY(mdr);ローカル座標系を回転。 -
translate(M_R, 0, 0);ローカル座標系を外側に移動。 -
drawMoon();『月』の描画。
-
}-
popMatrix();マトリクスを復帰。
-
}-
popMatrix();マトリクスを復帰。
-
マスター「ここで重要なのは、月の描画だ」
マスター「地球を描くための座標変換をした後、」
マスター「月を描画する時点では」
マスター「まだ popMatrix() によるマトリクスの復帰は行っていない」
マスター「だから月のローカル座標座標系は」
マスター「地球用の回転と平行移動に」
マスター「月用の回転と平行移動が合成されているんだ」
なお、ここでは pushMatrix() を 2 重に使っていることを分かりやすくするために、ブロック {} で囲み、インデントを付けているが、これは必要なものではない。
パダワン「おお!回りながら回ってる!」
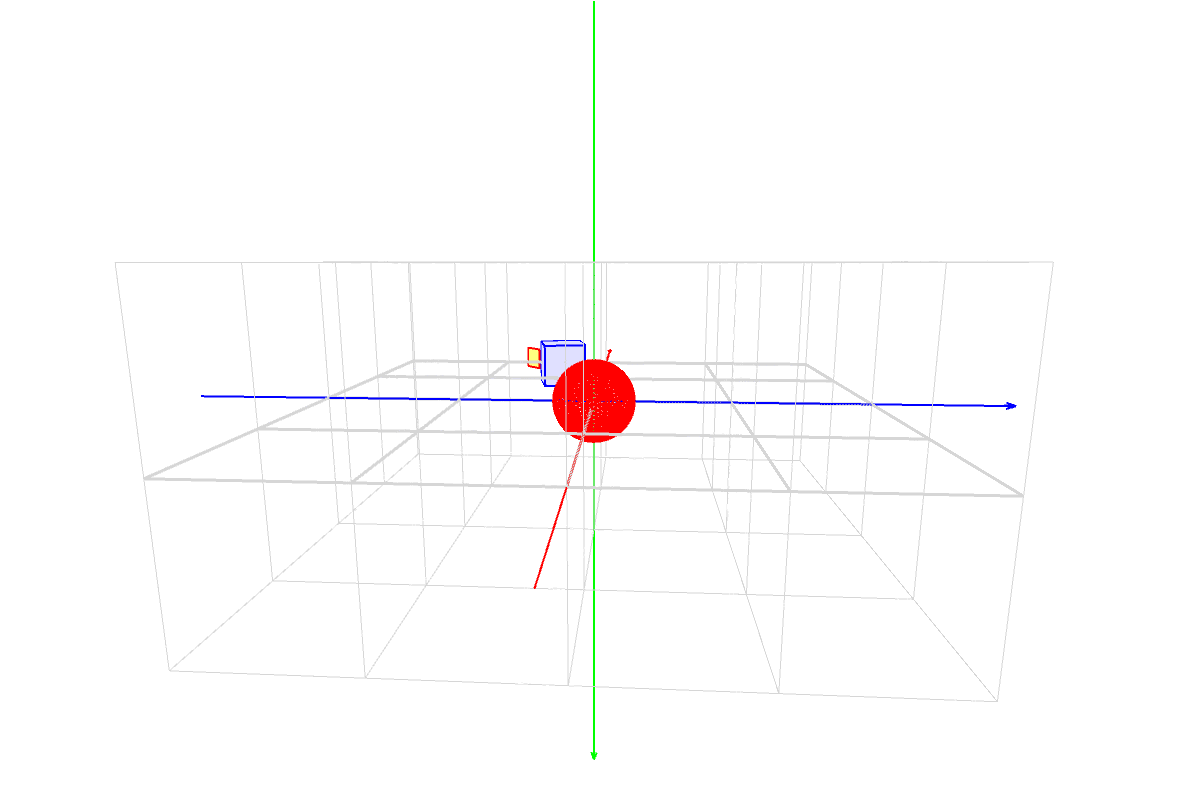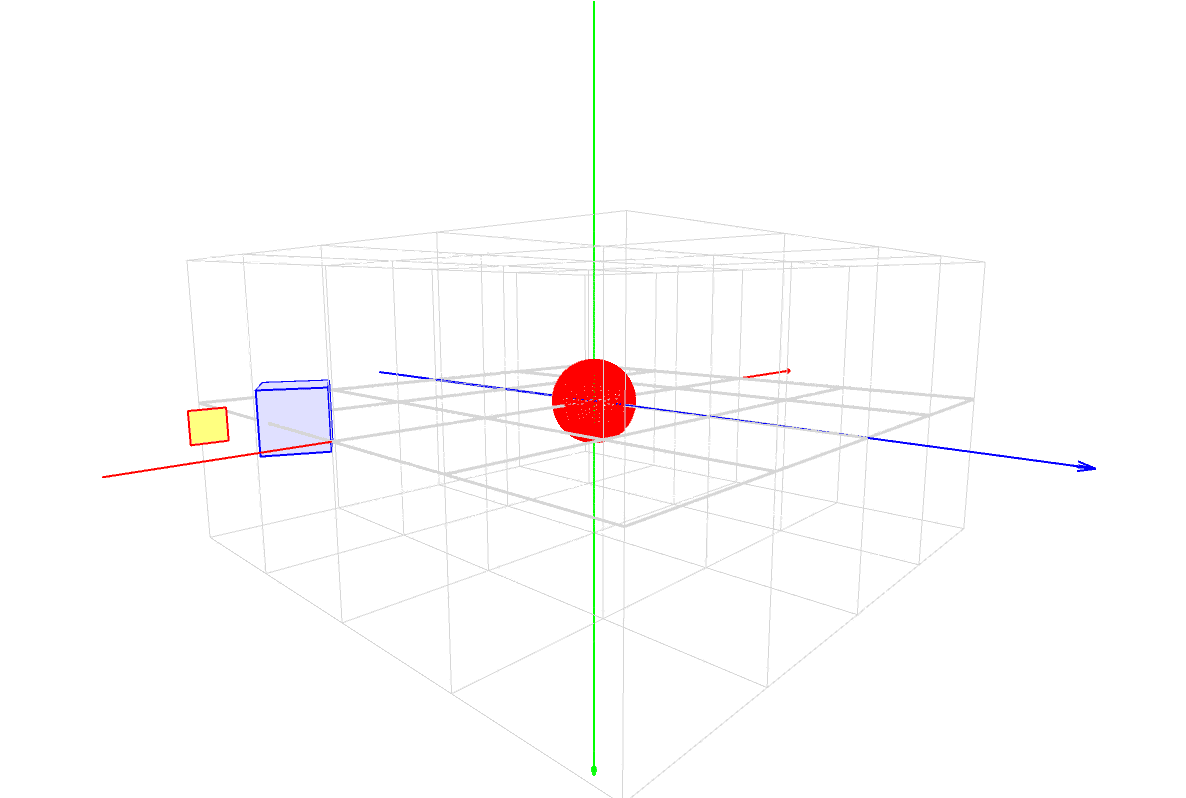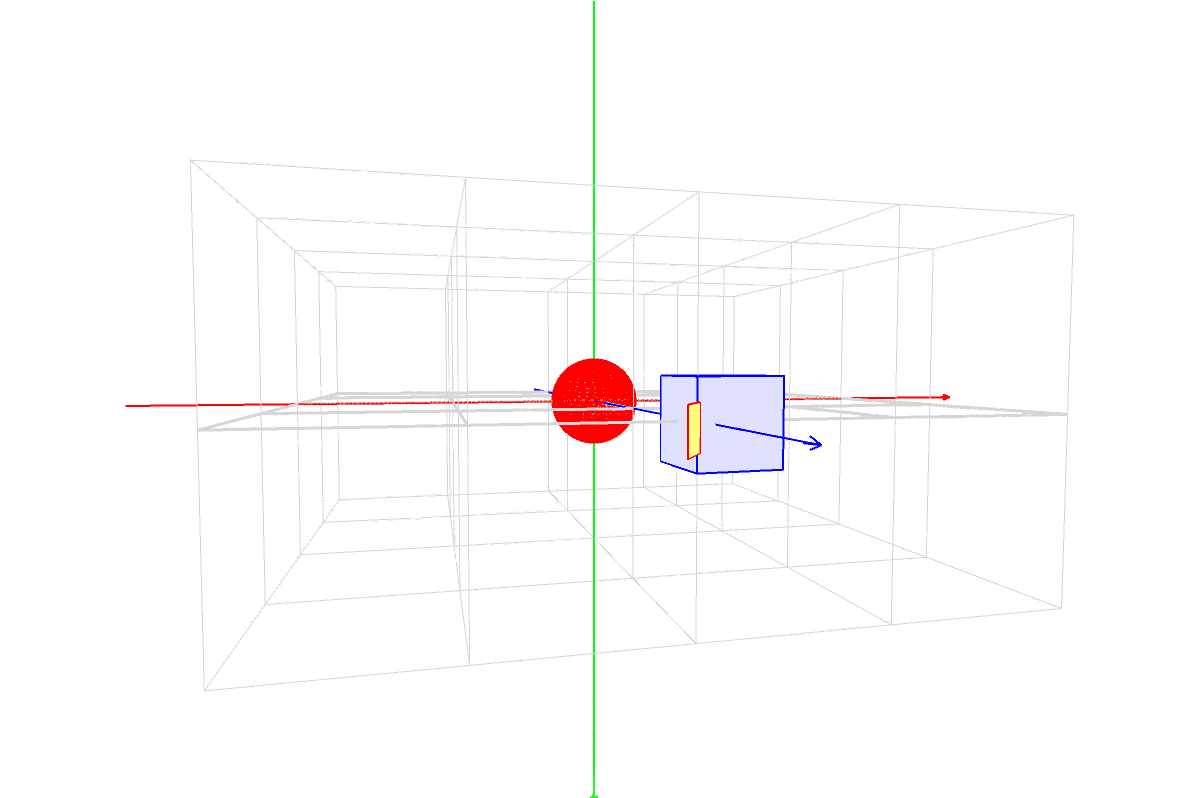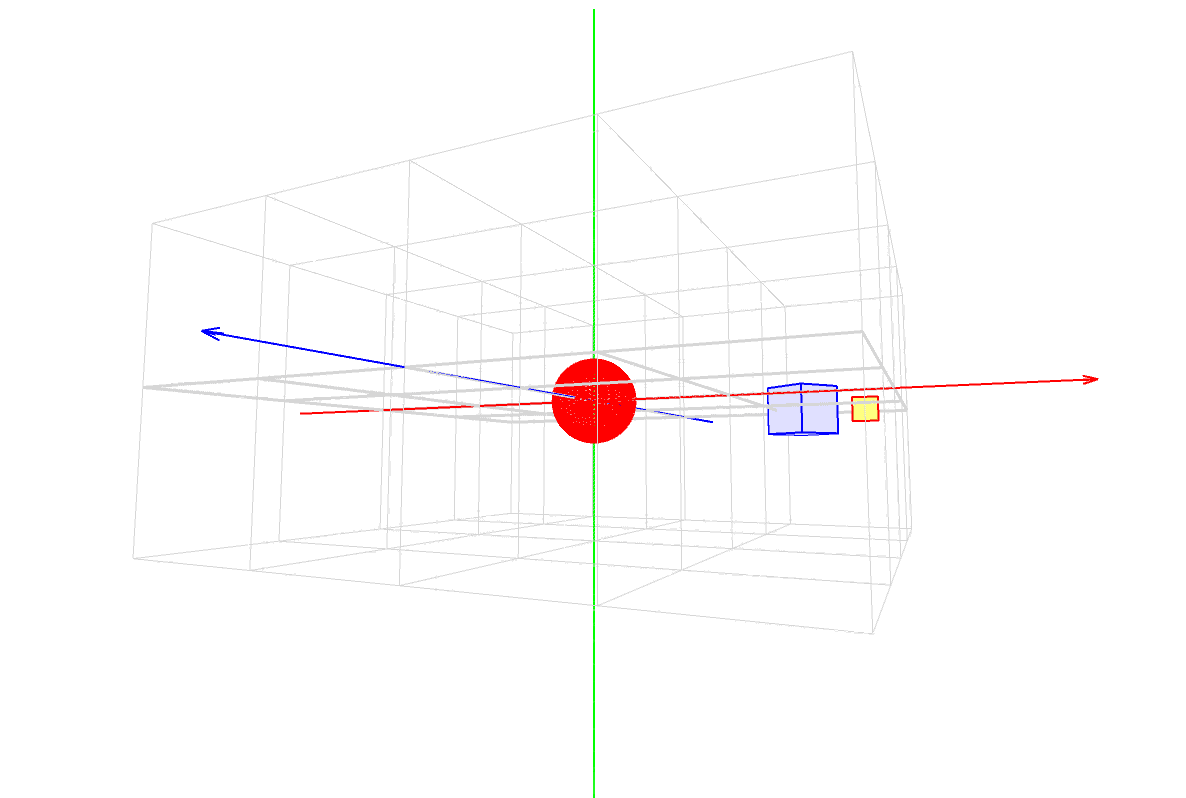
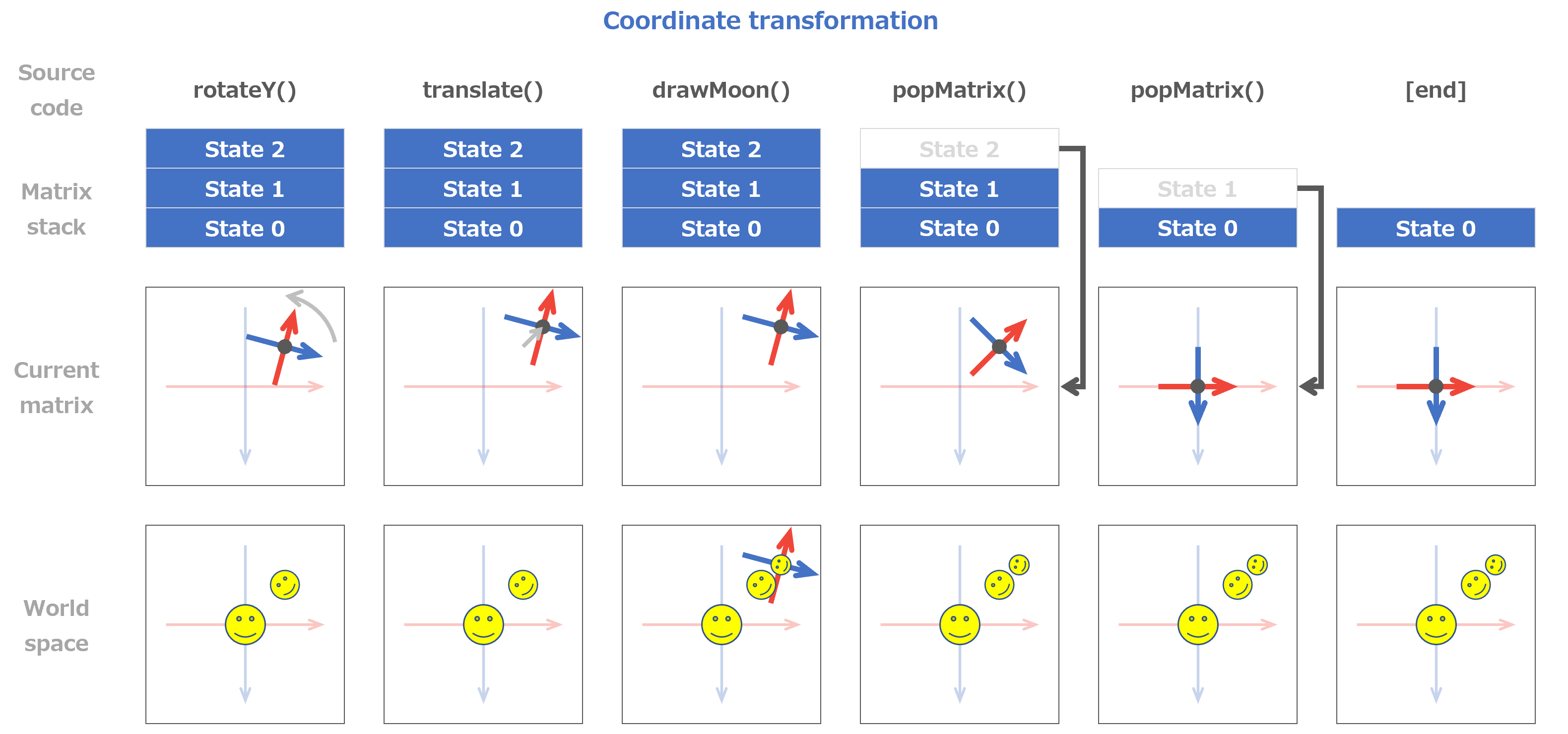
マスター「このセーバーの、スタックやマトリクスの状態遷移だが、」
マスター「今回は、既に太陽が描画された状態から始まっている」
マスター「まずは、地球を描画して、月用の pushmatrix() を実行するまでだ」
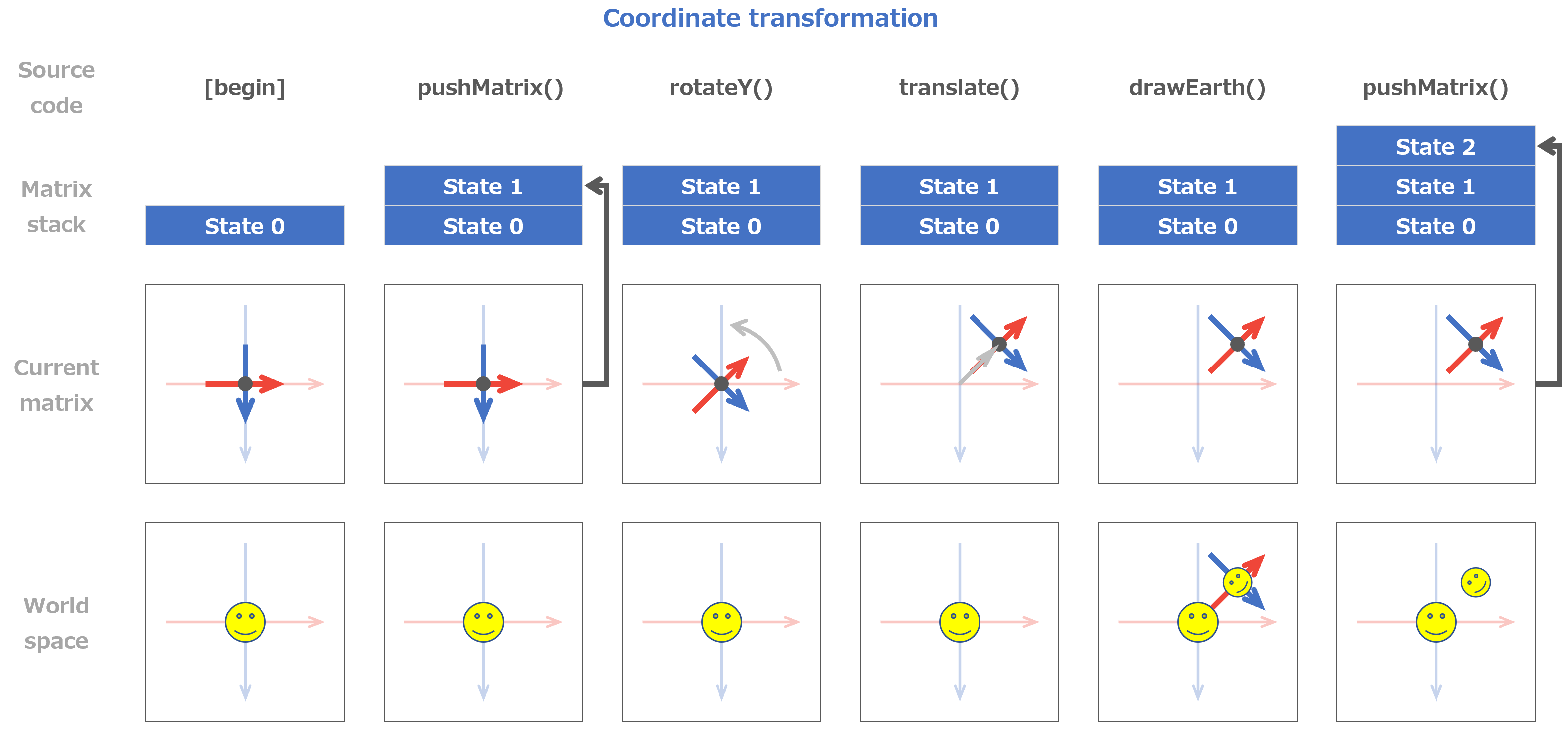
マスター「理解できるか?」
パダワン「うん!楽勝!」
パダワン「だって、これって、、」
パダワン「ポッドレーサーでコーナー回りながら、」
パダワン「目が回ってるみたいなもんでしょ!」
マスター(な、なんと、、)
マスター(まあ体では理解していそうだな)
マスター(少々不安は残るが …)
午前 2 時|テクスチャマッピングとカメラ
2 時 00 分|主役登場
マスター「いかん。もうこんな時間か …」
マスター「パダワンよ」
マスター「朝までに 3D オブジェクトでの実装は難しいかもしれない」
マスター「だから、2D オブジェクトへ」
マスター「テクスチャマッピングをする方法を伝授しておく」
パダワン「テクスチャ???」
マスター「そう。これは『ビルボード』という」
マスター「かつてよく使われていた、古(いにしえ)の技術だ」
マスター「つまり、3 次元空間上へ」
マスター「オブジェクトを『看板』のように配置する」
マスター「疑似 3D のことだ」
パダワン「あ、それって『書き割り』のこと?」
パダワン「それなら、僕、イニシエイト時代に」
パダワン「お楽しみ会の劇でやったよ!」
パダワン「あの時、夢だった『草』の役をゲットしたんだ!」
パダワン「なんでか分かんないけど、」
パダワン「砂漠のタトゥイーンでは大人気だった『草』の役が」
パダワン「コルサントではそれほど人気なかったんだよねえ」
パダワン「だから楽勝で役を勝ち取れたんだ」
パダワン「嬉しかったなあ」
するとそこへ Gopher君が顔を表した。
パダワン「なんだよ! Gopher君!」
パダワン「遅すぎっしょ!!!」
パダワン「困るんだよねぇ!」
パダワン「主役なんだから」
パダワン「入り時間はキッチリと守ってもらわないと!」
マスター「まあそう言うな」
マスター「Gopher君もいろいろと忙しいのだ」
マスター「ちょうどいいところへ来てくれた」
マスター「Gopher君、ポートレートを撮らせてくれないか」
そう言うと、マスターはホロカムのシャッターを切った。
マスター「PNG モードで出力したから、」
マスター「スケッチフォルダーに」
マスター「data という名前のディレクトリを作成して、」
マスター「そこにこれをコピーし」
マスター「 gopher.png という名前で保存するんだ」

キャラクター「Gopher君」 は、Renée French さん がデザインした Go マスコットがベースになっており、CC BY 3.0 のライセンスが付与されています。
マスター「スケッチフォルダーは」」
マスター「 [スケッチ][スケッチフォルダーを開く] で開くことができる」
any-dir
Learning
├── Learning.pde
├── DevUtils.pde
└── data <--- 作成
└── gopher.png <--- コピー
マスター「PNG をコピーしたら、次のように入力するんだ」
...
void draw() {
...
//updateObject10(); // <===== コメントアウト =====
updateObject11(); // <===== 追記 =====
}
...
// (11) テクスチャマッピング(静止) // <===== これ以降追記↓ =====
void drawGopher() {
PImage img = loadImage("gopher.png");
int h = img.height;
int w = img.width;
noStroke(); // 枠線を描画しない
beginShape();
texture(img);
vertex(-150, -150, 0, 0, 0);
vertex( 150, -150, 0, w, 0);
vertex( 150, 150, 0, w, h);
vertex(-150, 150, 0, 0, h);
endShape();
}
void updateObject11() {
drawGopher();
}
マスター「説明する」
-
void drawGopher() {...}
Gopher君を描画するメソッドだ。-
PImage img = loadImage("gopher.png");
スケッチフォルダー配下の data ディレクトリに配置した画像ファイルをこのようにロードすることができる。 int h = img.height;-
int w = img.width;
画像のサイズもこのように簡単に取り出せる。 -
noStroke();
この後で矩形にテクスチャを張り付けるが、枠線は不要なのでこのようにしている。 - beginShape();
シェイプの描画を開始する宣言。 - texture(img);
ここでこのシェイプに張り付けるテクスチャの画像を指定している。 - vertex();
4 つの頂点を指定しているが、これまでの使い方よりもパラメータが 2 つほど多い。詳細はこの後で説明する。 -
endShape();
シェイプの終了を宣言しているが、枠線を表示しないため、パラメータの CLOSE は必要はない。
-
-
void updateObject11() {...}
drawGopher() を呼び出しているだけだ。
マスター「頂点の指定の仕方は次のとおりだ」
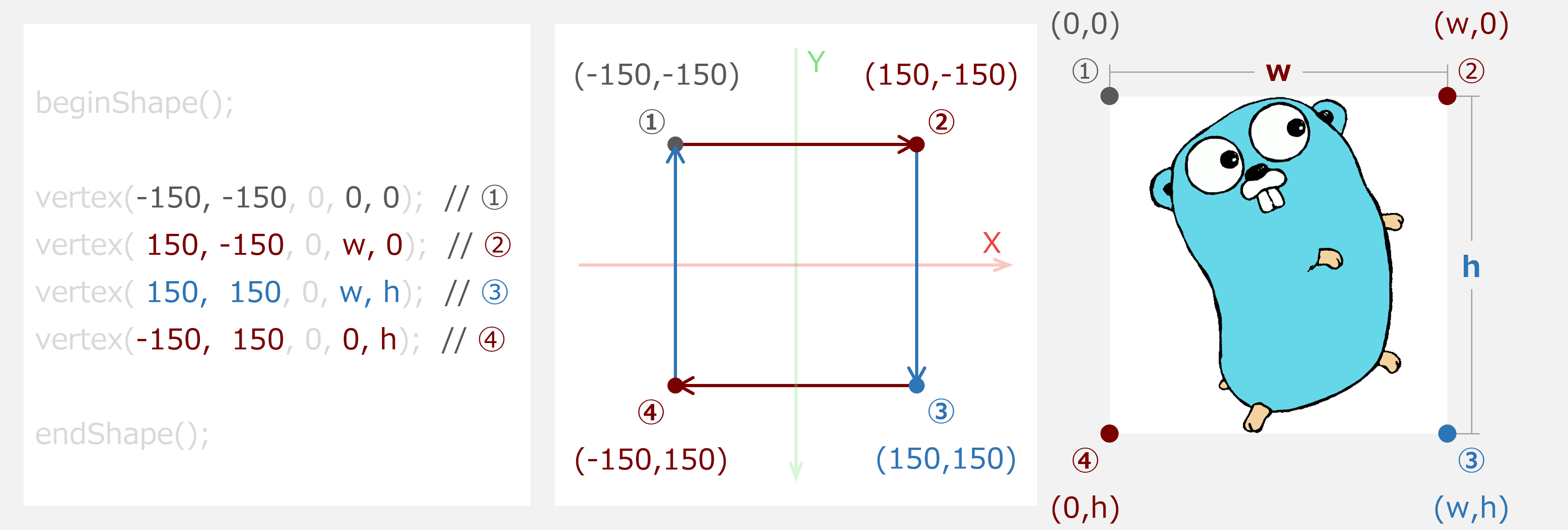
マスター「シェイプ側と画像側でサイズが合わない場合は」
マスター「シェイプ側にフィットするように画像の拡大縮小が行われるんだ」
マスター「そしてシェイプ側と画像側が相似形ではない場合は」
マスター「縦横比が崩れるため注意が必要だ」
マスター「なお、Processing で透明部分を含む画像を表示すると」
マスター「透明であるにも関わらず」
マスター「その背後のオブジェクトが隠れてしまうことがある」
マスター「そのような場合は setup() メソッドに以下の 1 行を追記するんだ」
...
void setup() {
size(1200, 800, P3D);
hint(ENABLE_DEPTH_SORT); // <===== 追記 =====
//setCameraOrbitalRadius(150);
//setCameraOrbitalPeriod(120);
frameRate(24);
}
...
マスター「そうしたら、このメソッドをサイズ指定できるように修正してみよう」
...
// (11) テクスチャマッピング(静止) // <===== これ以降修正↓ =====
void drawGopher(float len) { // <===== 修正 =====
PImage img = loadImage("gopher.png");
int h = img.height;
int w = img.width;
noStroke(); // 枠線を描画しない
beginShape();
texture(img);
vertex(-len/2, -len/2, 0, 0, 0); // <===== 修正 =====
vertex( len/2, -len/2, 0, w, 0); // <===== 修正 =====
vertex( len/2, len/2, 0, w, h); // <===== 修正 =====
vertex(-len/2, len/2, 0, 0, h); // <===== 修正 =====
endShape();
}
void updateObject11() {
drawGopher(100); // <===== 修正 =====
}
マスター「簡単に説明すると」
-
void drawGopher(int len)
表示する矩形(正方形)の 1 辺の長さを指定できるようにしている。 -
vertex(-len/2, -len/2, 0, 0, 0);以降
パラメータの len を使って頂点を指定している。 -
drawGopher(100);
矩形の 1 辺が 100 になるように指定している。
パダワン「お、ぺったんこが、ちっこくなった(笑)」
2 時 10 分|公転体の周りを公転
マスター「次のように入力するんだ」
...
void draw() {
...
//updateObject11(); // <===== コメントアウト =====
updateObject12(); // <===== 追記 =====
}
...
// (12) テクスチャマッピング(座標変換で公転体の周りを公転) // <===== これ以降追記↓ =====
// 動きは (10) とほぼ同じ
void updateObject12() {
float ms = millis(); // プログラム開始時点からの経過ミリ秒
final float S_LEN = 200; // 太陽Gopherの1辺の長さ
final float E_LEN = 100; // 地球Gopherの1辺の長さ
final float E_R = 400; // 地球Gopherの公転半径
final float E_SPEED = 80; // 地球Gopherの角度(Degree)/秒
float edd = ms * E_SPEED / 1000; // 地球Gopherの移動角度(Degree)
float edr = radians(edd); // 地球Gopherの移動角度(Radian)
final float M_LEN = 50; // 月Gopherの1辺の長さ
final float M_R = 100; // 月Gopherの公転半径
final float M_SPEED = 200; // 月Gopherの角度(Degree)/秒
float mdd = ms * M_SPEED / 1000; // 月Gopherの移動角度(Degree)
float mdr = radians(mdd); // 月Gopherの移動角度(Radian)
pushMatrix();
{
translate(0, -S_LEN / 2, 0);
drawGopher(S_LEN); // 太陽Gopher
}
popMatrix();
pushMatrix();
{
rotateY(edr);
translate(E_R, 0, 0);
pushMatrix();
{
translate(0, -E_LEN / 2, 0);
drawGopher(E_LEN); // 地球Gopher
}
popMatrix();
pushMatrix();
{
rotateY(mdr);
translate(M_R, -M_LEN / 2, 0);
drawGopher(M_LEN); // 月Gopher
}
popMatrix();
}
popMatrix();
}
マスター「これはさっきの」
マスター「太陽の周りを地球と月が公転するメソッドを」
マスター「Gopher君用に少し書き変えたものだ」
マスター「ほとんど違いはないが …」
マスター「各 Gopher君の足元が ZX 平面に接するようにしている」
マスター「このため各Gopher君を translate() で」
マスター「垂直方向 (Y 軸方向) に矩形の 1 辺の長さの半分だけずらしている」
マスター「だが、その影響を他のオブジェクトへ与えたくないから」
マスター「前後でマトリクスの退避と復帰を行っているんだ」
pushMatrix(); // マトリクスの退避
{
// このブロック内の座標変換は地球と月の位置や姿勢に影響しない
translate(0, -S_LEN / 2, 0); // 垂直方向に矩形の辺の長さの半分ずらす
drawGopher(S_LEN); // 太陽Gopher
}
popMatrix(); // マトリクスの復帰
マスター「そして、地球Gopher君については」
マスター「垂直方向 (Y 軸方向) と水平方向 (X軸、Z軸方向) の移動成分を分け、」
マスター「回転と水平方向の移動成分だけが月Gopher君に影響するようにしている」
// 地球の公転用の座標変換
// 以下の2行(回転との水平方向の移動)は月の位置や姿勢に影響する
rotateY(edr);
translate(E_R, 0, 0); // 垂直方向の移動成分は含まない
pushMatrix(); // マトリクスの退避
{
// このブロック内の座標変換は月に影響しない
translate(0, -E_LEN / 2, 0); // 垂直方向の移動成分
drawGopher(E_LEN); // 地球Gopher
}
popMatrix(); // マトリクスの復帰
// 以降、月の座標変換と描画
そう言いながらパダワンは [実行] ボタンをクリックした。
パダワン「おお!」
パダワン「すげっ!!!」
2 時 20 分|ビルボード
マスター「でも、これは問題があるんだ」
パダワン「ぺったんこがバレちゃうね(笑)」
マスター「そう。だから、」
マスター「これから、それがバレないようにするぞ!」
マスター「次のように入力するんだ」
...
void draw() {
...
//updateObject12(); // <===== コメントアウト =====
updateObject13(); // <===== 追記 =====
}
...
// (13) ビルボード(座標変換で公転体の周りを公転) // <===== これ以降追記↓ =====
// 動きは (12) とほぼ同じ
void turnToCamera() { // <== +
PMatrix3D m = (PMatrix3D)g.getMatrix(); // <== +
// <== +
//column 0 //column 1 //column 2 // <== +
m.m00 = 1; m.m01 = 0; m.m02 = 0; // row 0 // <== +
m.m10 = 0; m.m11 = 1; m.m12 = 0; // row 1 // <== +
m.m20 = 0; m.m21 = 0; m.m22 = 1; // row 2 // <== +
// <== +
resetMatrix(); // <== +
applyMatrix(m); // <== +
} // <== +
void updateObject13() { // <== +
float ms = millis(); // プログラム開始時点からの経過ミリ秒
final float S_LEN = 200; // 太陽Gopherの1辺の長さ
final float E_LEN = 100; // 地球Gopherの1辺の長さ
final float E_R = 400; // 地球Gopherの公転半径
final float E_SPEED = 80; // 地球Gopherの角度(Degree)/秒
float edd = ms * E_SPEED / 1000; // 地球Gopherの移動角度(Degree)
float edr = radians(edd); // 地球Gopherの移動角度(Radian)
final float M_LEN = 50; // 月Gopherの1辺の長さ
final float M_R = 100; // 月Gopherの公転半径
final float M_SPEED = 200; // 月Gopherの角度(Degree)/秒
float mdd = ms * M_SPEED / 1000; // 月Gopherの移動角度(Degree)
float mdr = radians(mdd); // 月Gopherの移動角度(Radian)
pushMatrix();
{
translate(0, -S_LEN / 2, 0);
turnToCamera(); // <== +
drawGopher(S_LEN); // 太陽Gopher
}
popMatrix();
pushMatrix();
{
rotateY(edr);
translate(E_R, 0, 0);
pushMatrix();
{
translate(0, -E_LEN / 2, 0);
turnToCamera(); // <== +
drawGopher(E_LEN); // 地球Gopher
}
popMatrix();
pushMatrix();
{
rotateY(mdr);
translate(M_R, -M_LEN / 2, 0);
turnToCamera(); // <== +
drawGopher(M_LEN); // 月Gopher
}
popMatrix();
}
popMatrix();
}
マスター「ひとつ前とほとんど同じだが、」
マスター「追記した箇所に // <== + を付けている」
マスター「簡単に説明する」
-
void turnToCamera() {...}
このメソッドの内容については後で詳しく説明するが、描画直前にこれを呼び出せば、矩形に貼り付けたテクスチャが常にカメラの方向を向くように姿勢制御することができる。
だが以下の点に注意が必要だ。- ローカル座標系で XY 平面(またはこれに平行な面)に貼り付けたテクスチャでなければ、このメソッドは機能しない。
- このメソッドをコールすれば、テクスチャが貼りついた面がスクリーンの面と平行になるが、これは厳密な意味でカメラの視点方向に面を向けている訳ではないということを意味している。このため、スクリーンの端に映るオブジェクトは若干の歪みが生ずるはずだ。
-
void updateObject13() {...}
各オブジェクトの描画直前にturnToCamera()を呼び出している。
マスター「ちなみに、ZX 平面だけで考えた場合、」
マスター「下図の左側が「ビルボードの厳密な変換」で
マスター「メソッド turnToCamera() の変換が右側だ」
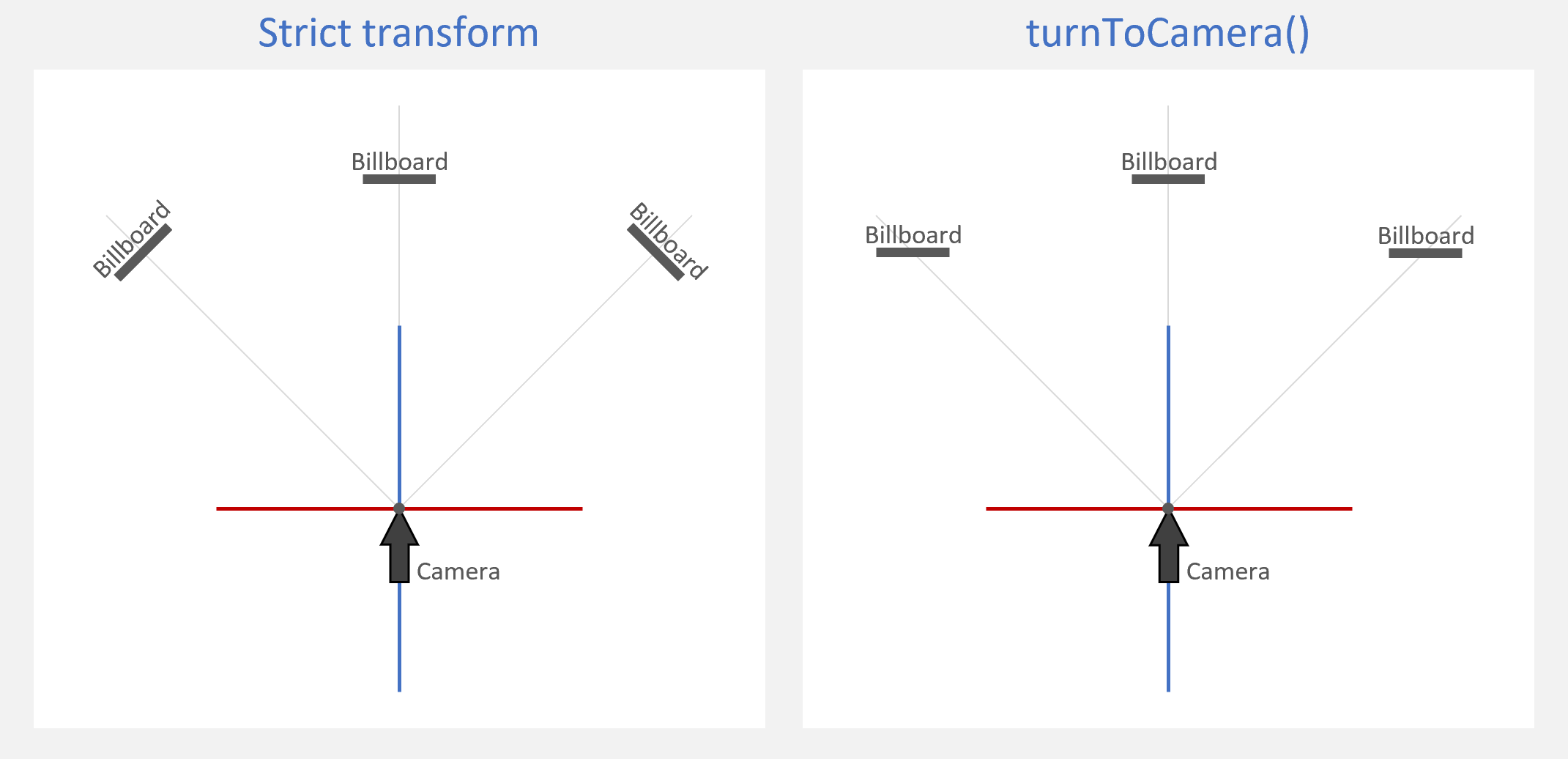
パダワン「バレなきゃなんでもいいっしょ!」
そう言いながらパダワンは [実行] ボタンをクリックした。
パダワン「お、ぺったんこが分かんなくなった!」

マスター「なお、想定通りの円運動になっているかどうかを」
マスター「もっと上方や下方からの視点で確認したいというなら」
マスター「ユーティリティを使って以下のようにすれば良いだろう」
...
void setup() {
size(1200, 800, P3D);
hint(ENABLE_DEPTH_SORT);
//setCameraOrbitalRadius(150);
//setCameraOrbitalPeriod(120);
setCameraMaxDepth(1500); // <===== 追記 =====
frameRate(24);
}
...
2 時 30 分|カメラを制御する(静止)
マスター「これまで」
マスター「ユーティリティの自動制御に任せていたカメラを、」
マスター「自分で制御する方法を伝授する」
マスター「次のように入力するんだ」
...
void setup() {
size(1200, 800, P3D);
hint(ENABLE_DEPTH_SORT);
//setCameraOrbitalRadius(150);
//setCameraOrbitalPeriod(120);
//setCameraMaxDepth(1500);
setDevRoomAutoCameraEnabled(false); // <===== 追記 =====
frameRate(24);
}
...
void draw() {
background(255, 255, 255);
updateCamera1(); // <===== 追記 =====
updateDevRoom();
//updateObject1();
//updateObject2();
//updateObject3();
//updateObject4();
//updateObject5();
//updateObject6();
//updateObject7();
//updateObject8();
//updateObject9();
//updateObject10()
//updateObject11();
//updateObject12();
updateObject13();
}
...
// (14) カメラ制御(静止) // <===== これ以降追記↓ =====
void updateCamera1() {
float x = 25;
float y = -70;
float z = 800;
camera(x, y, z, 0, 0, 0, 0, 1, 0);
}
マスター「説明する」
-
void setup() {...}-
setDevRoomAutoCameraEnabled(false);
ユーティリティのカメラの自動制御機能を off にする設定だ。これはframeRate()より先に呼び出す必要がある。
-
-
void draw() {...}-
updateCamera1();
この後で書く、カメラを制御するメソッドの呼び出しだ。これは各オブジェクトを描画する前に呼び出す必要がある。
-
-
void updateCamera1() {...}-
xyz
カメラの視点を置く座標だ。 -
camera(x, y, z, 0, 0, 0, 0, 1, 0);
カメラを制御するための Processing のメソッドで、引数の順に意味は以下のようになっている。-
eyeX視点(カメラの位置)の X 座標 -
eyeY視点(カメラの位置)の Y 座標 -
eyeZ視点(カメラの位置)の Z 座標 -
centerX視線の先(スクリーン中央に合わせる点の座標)の X 座標 -
centerY視線の先(スクリーン中央に合わせる点の座標)の Y 座標 -
centerZ視線の先(スクリーン中央に合わせる点の座標)の Z 座標 -
upXカメラの上方向を示すベクトル (0 or -1 or 1) -
upYカメラの上方向を示すベクトル (0 or -1 or 1) -
upZカメラの上方向を示すベクトル (0 or -1 or 1)
-
-
マスター「つまり、このカメラ設定は、」
マスター「座標 (25, -75, 800) にカメラを持っていき、」
マスター「座標 (0, 0, 0) にレンズを向け、」
マスター「カメラの頭を Y 軸のダークサイド(負の無限大方向)に向ける」
マスター「という意味だ」
マスター「もう一度次の図とにらめっこしながら」
マスター「カメラを置く座標とスクリーンに映る映像を頭に思い描くんだ」

スクリーンに描く映像を頭に思い描きながら、パダワンは [実行] ボタンをクリックした。
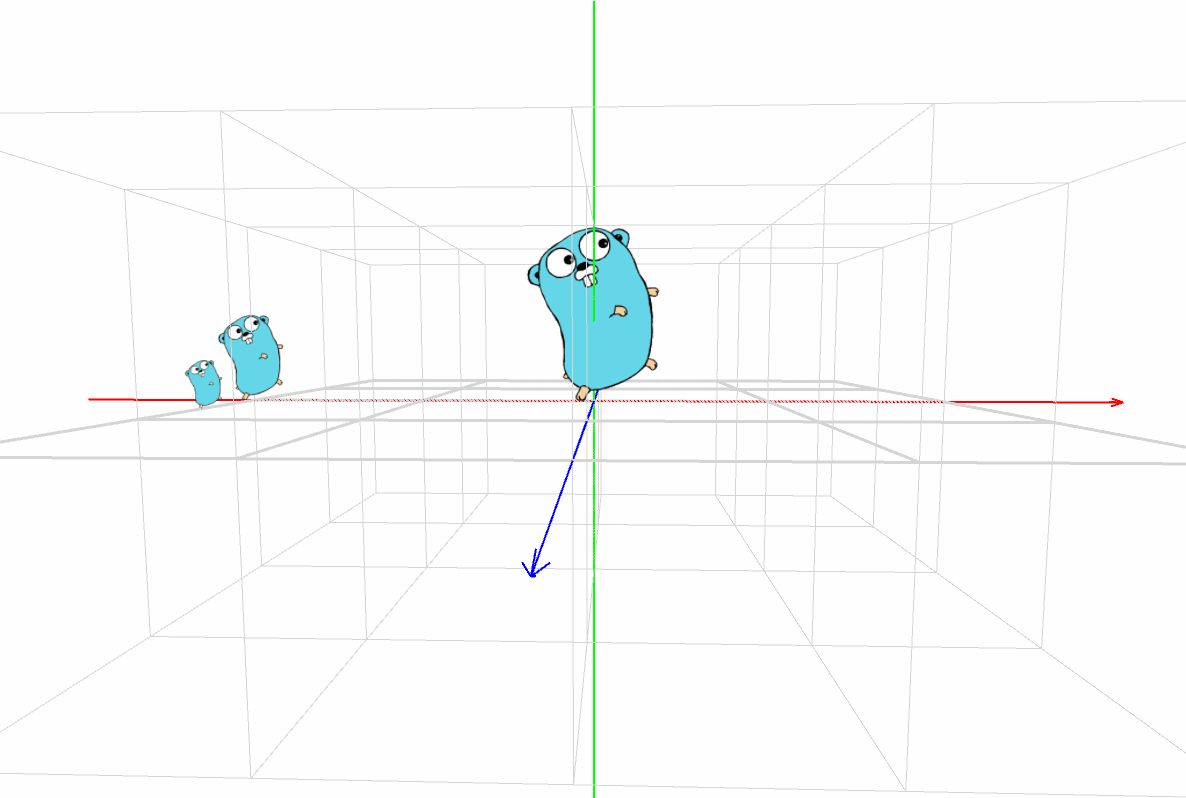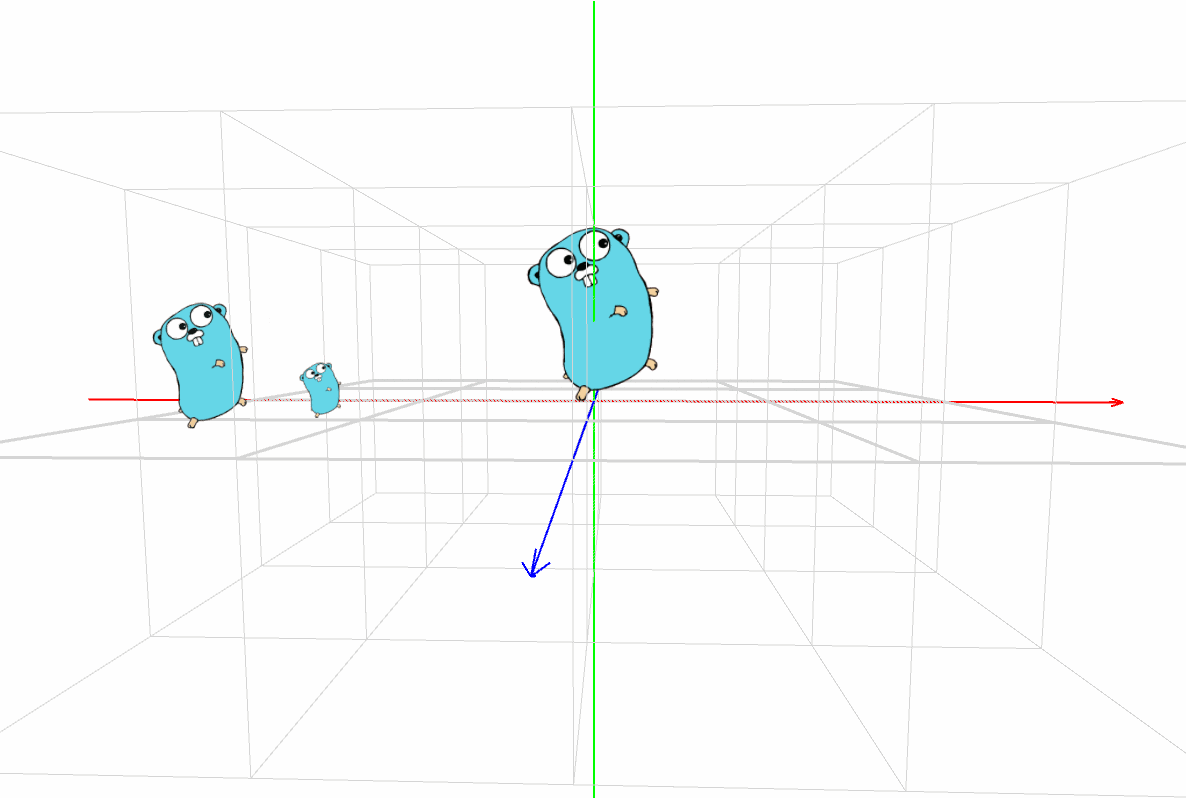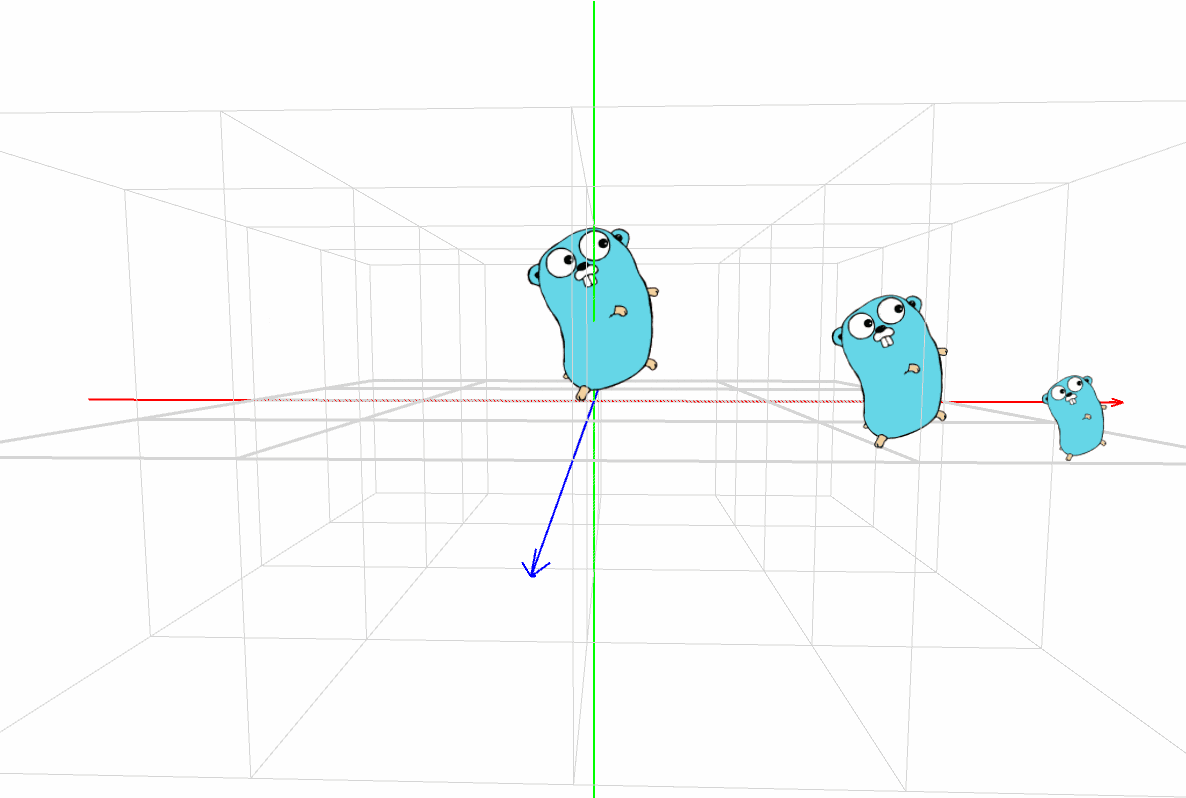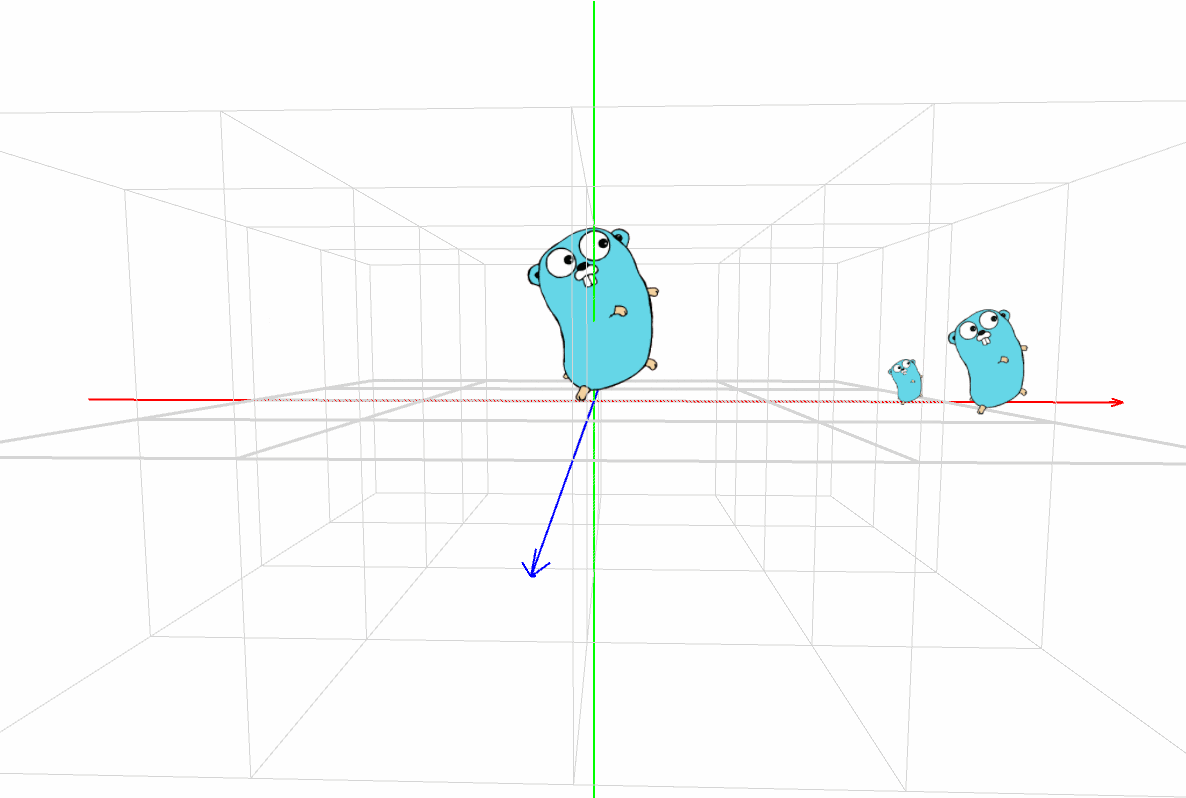
マスター「どうだ?イメージどおりだったか?」
パダワン「うん。Gopher君が3匹!!!」
2 時 40 分|カメラをまっすぐ動かす(等速直線運動)
マスター「それではカメラを動かしてみよう」
マスター「次のように入力するんだ」
...
void draw() {
...
//updateCamera1(); // <===== コメントアウト =====
updateCamera2(); // <===== 追記 =====
...
}
...
// (15)カメラ制御(等速直線運動) // <===== これ以降追記↓ =====
void updateCamera2() {
final float START_Z = 1500; // 開始時点のZ座標
final float SPEED = -300; // 秒速-300
float ms = millis(); // プログラム開始時点からの経過ミリ秒
float dz = ms * SPEED / 1000; // 移動距離(Y座標)
float x = 100;
float y = -50;
float z = START_Z + dz; // 現在位置(Y座標)
camera(x, y, z, x, y, z-1, 0, 1, 0);
//camera(x, y, z, 0, 0, 0, 0, 1, 0);
}
マスター「説明する」
-
START_ZSPEEDmsdz
カメラの開始地点や移動速度を定めている。オブジェクトを移動させた時とほとんど同じだ。 -
xyz
カメラの現在地の座標を表す変数だ。描画の度に z 座標だけが変化するようにしている。 -
camera(x, y, z, x, y, z-1, 0, 1, 0);
カメラの制御だ。座標 (x, y, z) から、座標 (x, y, z-1) を見つめるとどうなるかを想像するんだ。 -
//camera(x, y, z, 0, 0, 0, 0, 1, 0);
コメントアウトしているが、上とは少し異なるカメラ制御になっている。座標 (x, y, z) から、座標 (0, 0, 0) を見つめるとどうなるかを想像するんだ。
パダワンは [実行] ボタンをクリックした。

パダワン「おお!太陽Gopher君にぶつかるかと思った!」
マスター「確認できたら、コメントアウトしている方のカメラ制御も試してみるんだ」
...
//camera(x, y, z, x, y, z-1, 0, 1, 0);
camera(x, y, z, 0, 0, 0, 0, 1, 0);
...
2 時 50 分|カメラを公転させる(等速円運動)
マスター「次はカメラの公転だ」
...
void draw() {
background(255, 255, 255); // 背景色(R,G,B) は白
//updateCamera1();
//updateCamera2(); // <===== コメントアウト =====
updateCamera3(); // <===== 追記 =====
updateDevRoom();
updateObject1(); // <===== コメント外す =====
updateObject2(); // <===== コメント外す =====
updateObject3(); // <===== コメント外す =====
updateObject4(); // <===== コメント外す =====
//updateObject5();
//updateObject6();
//updateObject7();
//updateObject8();
//updateObject9();
//updateObject10()
//updateObject11();
//updateObject12();
//updateObject13(); // <===== コメントアウト =====
}
...
// (16) カメラ制御(公転) // <===== これ以降追記↓ =====
void updateCamera3() {
final float R = 1500; // 公転半径
final float SPEED = 15; // 角度(Degree)/秒
float ms = millis(); // プログラム開始時点からの経過ミリ秒
float dd = ms * SPEED / 1000; // 移動角度(Degree)
float dr = radians(dd); // 移動角度(Radian)
float x = R * cos(dr); // X座標
float z = R * sin(dr); // Z座標
float y = -50;
camera(x, y, z, 0, 0, 0, 0, 1, 0);
}
マスター「説明する」
-
draw() {...}
カメラ制御はupdateCamera3()を使用し、
描画するオブジェクトはupdateObject1()~updateObject4()としている。 -
void updateCamera3() {...}-
RSPEEDmsdddr
公転半径や回る速度など、オブジェクトを公転させた時と同様だ。 -
xyz
三角関数を使ってカメラを配置する座標を求めている。 -
camera(x, y, z, 0, 0, 0, 0, 1, 0);
ワールド座標系の原点 (0, 0, 0) を見つめるようにしている。
-

パダワン「おっ!Gopher君!!!」
パダワン「降板…?」
午前 3 時|モデル変換とビュー変換
3 時 00 分|マトリクスの正体
マスター「さて、ここまで」
マスター「translate() や rotate() を使って」
マスター「オブジェクトを自由に配置し、」
マスター「camera() を使って」
マスター「視点をどこに置き、世界をどう眺めるのか、」
マスター「その方法を学んできたわけだが、」
マスター「実はこれまで座標系と言っていたものは、」
マスター「空間上の点を、3 つの数の組 (x, y, z) で表現する」
マスター「直交座標系と呼ばれるものだ」
マスター「そして、」
マスター「Processing を含む多くの CG ライブラリなどでは、」
マスター「座標変換をする際に、」
マスター「空間上の点を、4 つの数の組で表現する」
マスター「同次座標系と呼ばれるものが使われているんだ」
パダワン「意味不明!!!」
パダワン「なんでわざわざ難しくすんの?」
マスター「がはは!そう思うだろ?」
マスター「ところが、この同次座標系を使うと」
マスター「平行移動や回転などの座標変換を」
マスター「とてもシンプルに表現できるようになるんだ」
マスター「銀河の歴史の中で幾多もの騎士たちが修練に修練を重ね、」
マスター「それを積み上げてきた結果編み出した偉大な技なんだよ」
マスター「[ファイル][新規] で新しいスケッチを開くんだ」
マスター「新しいスケッチを開いたら、[ファイル][名前を付けて保存...] で」
マスター「"Matrix" など、適当な名前を付けて保存しておこう」

マスター「スケッチを保存したら、以下を入力するんだ」
size(500,500,P3D);
// マトリクスの確認
println("----------------------------------");
resetMatrix(); println("resetMatrix();");
printMatrix();
translate(-3, 0, -3); println("translate(-3, 0, -3);");
printMatrix();
rotateY(radians(30)); println("rotateY(radians(30));");
printMatrix();
これを入力した後、パダワンが [実行] ボタンをクリックするとコンソールに以下のように出力された。
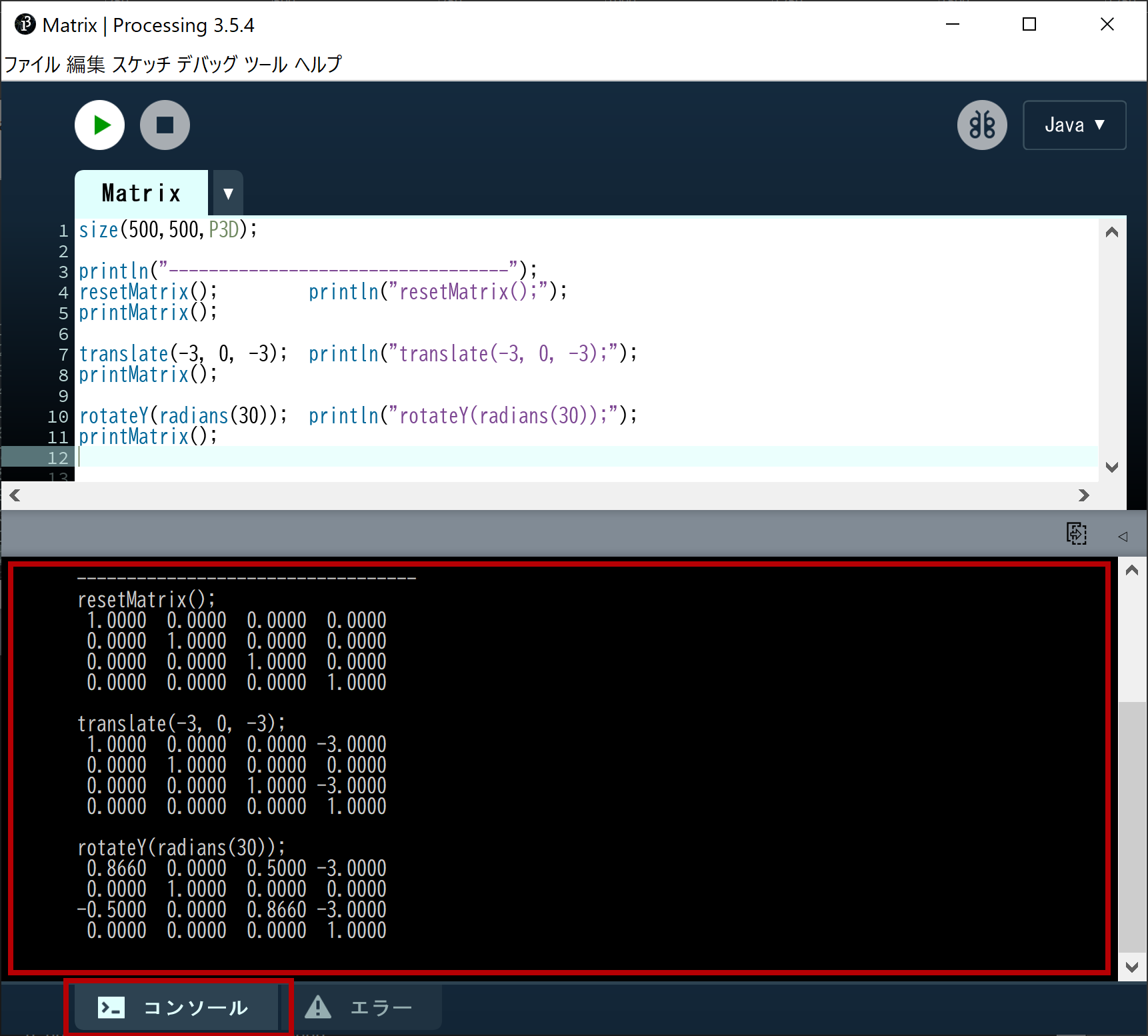
パダワン「なんだこれ???」
マスター「マトリクスの正体だ!」
パダワン「は???」
マスター「これまで退避させたり復帰させたりしていた」
マスター「マトリクスというものは、」
マスター「実は 16 個の数字の集まりで」
マスター「printMatrix() でその内容を表示することができる」
マスター「そして translate() や rotateY() などの座標変換は」
マスター「そのすべてをこの 16 個の値の組み合わせで表現することができるんだ」
パダワン「…」
マスター「イニシエイトで『行列』は習ったな?」
パダワン「うん!習った!」
パダワン「お店の行列とは違うってことは知ってる!」
マスター「コンソールに出力された最初の情報は」
マスター「resetMatrix() で初期化した後の」
マスター「現在のマトリクスの状態だ」
resetMatrix();
1.0000 0.0000 0.0000 0.0000
0.0000 1.0000 0.0000 0.0000
0.0000 0.0000 1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
マスター「座標変換の情報は、」
マスター「このように 4 行 × 4 列 の行列、つまり 4 次正方行列で表せるんだ」
マスター「そして resetMatrix() で初期化すると」
マスター「現在のマトリクスが 単位行列 になるんだ」
パダワン「???」
マスター「単位行列というのは」
マスター「行列の乗法における 単位元 のことで、」
マスター「普通の数で言えば」
マスター「足し算の 0 や、掛け算の 1 のような基本的な値のことだ」
マスター「どんな数字に 0 を足しても値は変わらないだろう?」
マスター「掛け算の場合は?」
パダワン「あ!どんな数字に 1 を掛けても変わらない!」
パダワン「気がする …」
マスター「そう。座標変換は行列の乗算で行われるんだ」
マスター「そして、どんな(行列の)値に掛けても」
マスター「それを変化させないのが 単位行列 だ」
パダワン「えーと、、」
パダワン「カウンターを初期化するときに 0 にするようなもん?」
マスター「まあそれで良いだろう」
マスター「そして translate(-3, 0, -3) を適用したマトリクスがこれで、」
translate(-3, 0, -3);
1.0000 0.0000 0.0000 -3.0000
0.0000 1.0000 0.0000 0.0000
0.0000 0.0000 1.0000 -3.0000
0.0000 0.0000 0.0000 1.0000
マスター「更に rotateY(radians(30)); を適用したマトリクスがこれだ」
rotateY(radians(30));
0.8660 0.0000 0.5000 -3.0000
0.0000 1.0000 0.0000 0.0000
-0.5000 0.0000 0.8660 -3.0000
0.0000 0.0000 0.0000 1.0000
マスター「それぞれの数字の意味は今は気にしなくていい」
マスター「だが、上のマトリクスには、 roatateY() だけではなく」
マスター「ひとつ前の translate() の変換も」
マスター「含まれていることに注意するんだ」
パダワン「えーと、、translate() を」
パダワン「pushMatrix() と popMatrix() で囲めば」
パダワン「回転だけになるの?」
マスター「疑問に思ったら、確かめてみるんだ」
パダワン「えーと、、」
パダワン「ここに push 入れて、、」
size(500,500,P3D);
// マトリクスの確認
println("----------------------------------");
resetMatrix(); println("resetMatrix();");
printMatrix();
pushMatrix(); // <== 追記
translate(-3, 0, -3); println("translate(-3, 0, -3);");
printMatrix();
popMatrix(); // <== 追記
rotateY(radians(30)); println("rotateY(radians(30));");
printMatrix();
パダワン「あ、ほんとだ」
パダワン「細かいことはわかんないけど、」
パダワン「右端の -3.0000 が消えてる!」
...
rotateY(radians(30));
0.8660 0.0000 0.5000 0.0000
0.0000 1.0000 0.0000 0.0000
-0.5000 0.0000 0.8660 0.0000
0.0000 0.0000 0.0000 1.0000
行列の乗法
マスター「ここまでを整理すると、」
マスター「ローカル座標系をワールド座標系に変換するために」
マスター「使ってきたマトリクスというものは」
マスター「16 個の数値の組み合わせでできていて」
マスター「これは 4 行 × 4 列の行列を表している」
マスター「そして、この値の組み合わせで」
マスター「こまでにやったすべての座標変換を表現できるんだ」
マスター「いいか?!」
パダワン「うん!なんとなくわかった!!!」
パダワン「気がしないわけでもない …」
マスター「そうしたら、このマトリクスが Processing の中で」
マスター「どのように計算されているかを少し考えてみよう」
マスター「まずは行列の乗法についておさらいだ」
マスター「基本の 4 行 1 列 と 1 行 4 列 の乗算は次のとおりだ」
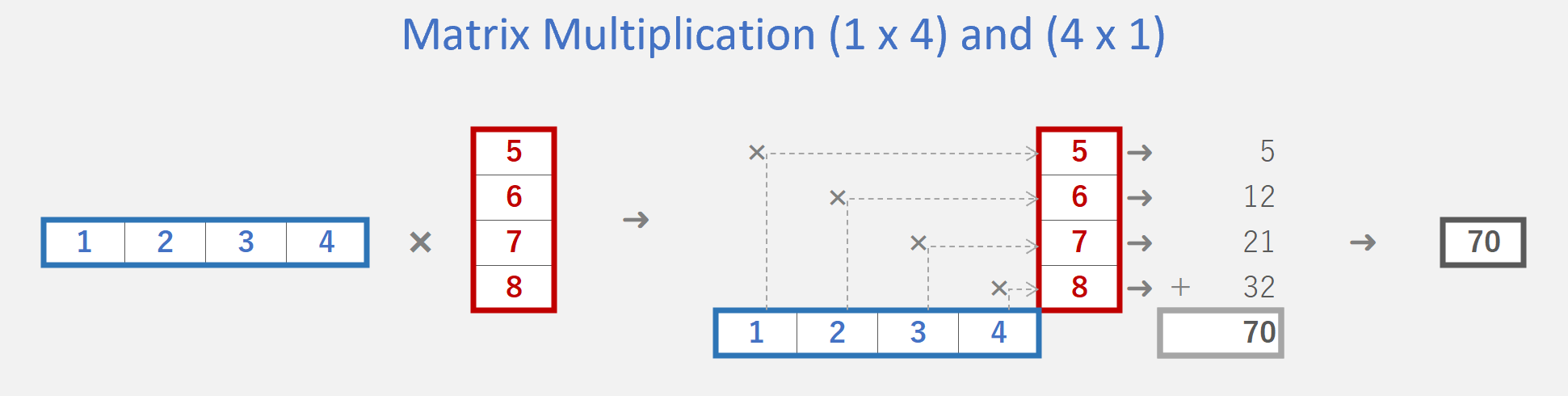
マスター「そして、4 行 4 列 と 4 行 1 列 の乗算は」
マスター「4 行 4 列の方を 1 行づつばらして計算すれば良い」
マスター「例えば」
マスター「 resetMatrix() と」
マスター「translate(-3, 0, -3) を実行した後に」
マスター「 Vertex(5, 0, 4) を実行して描画される」
マスター「ローカル座標上の頂点 P (5, 0, 4) は、」
マスター「(5, 0, 4) の後に 1 を追加して」
マスター「4 行 1 列の行列にしてから」
マスター「以下のように計算すると、」
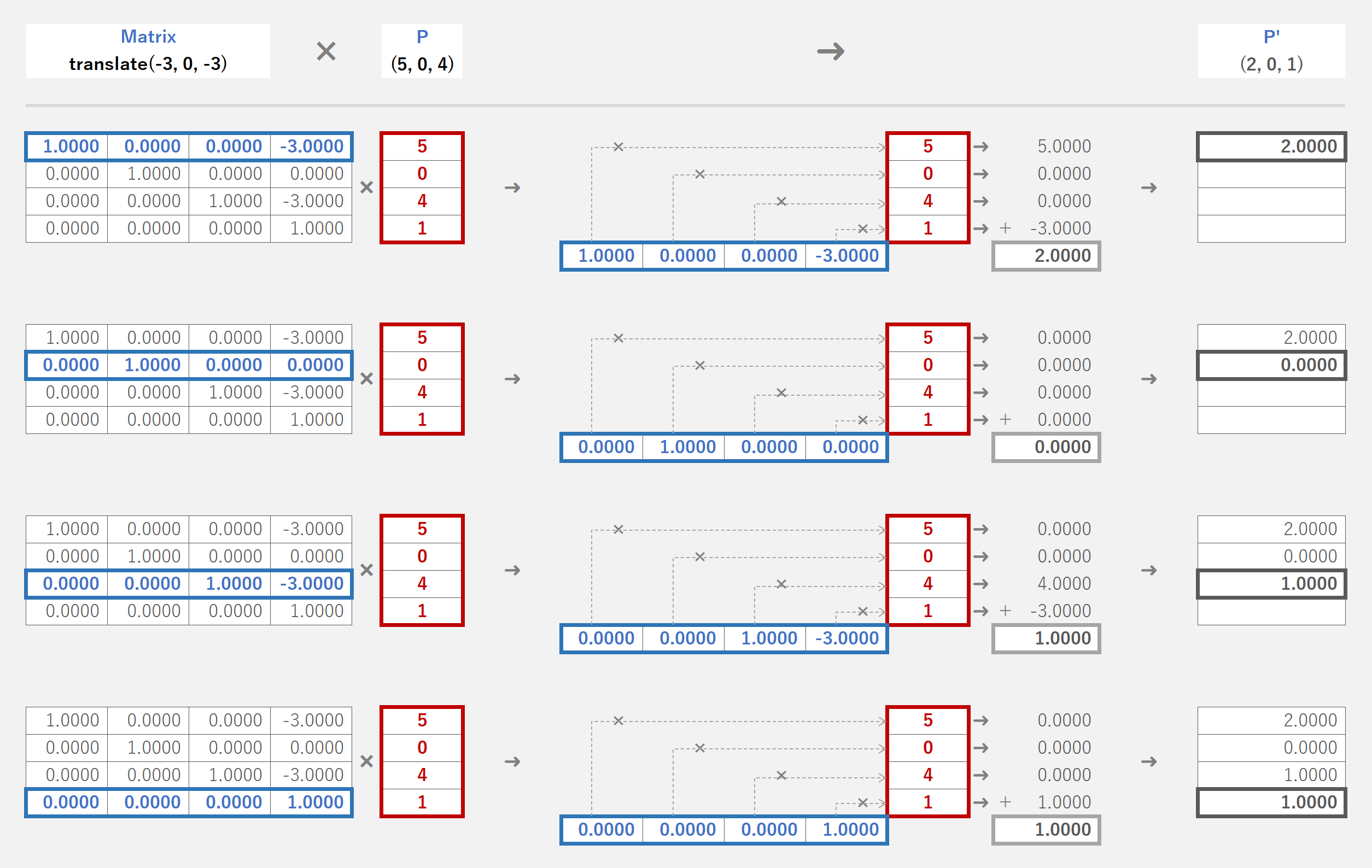
マスター「ワールド座標の 頂点 P' (2, 0, 1) に変換されるんだ」
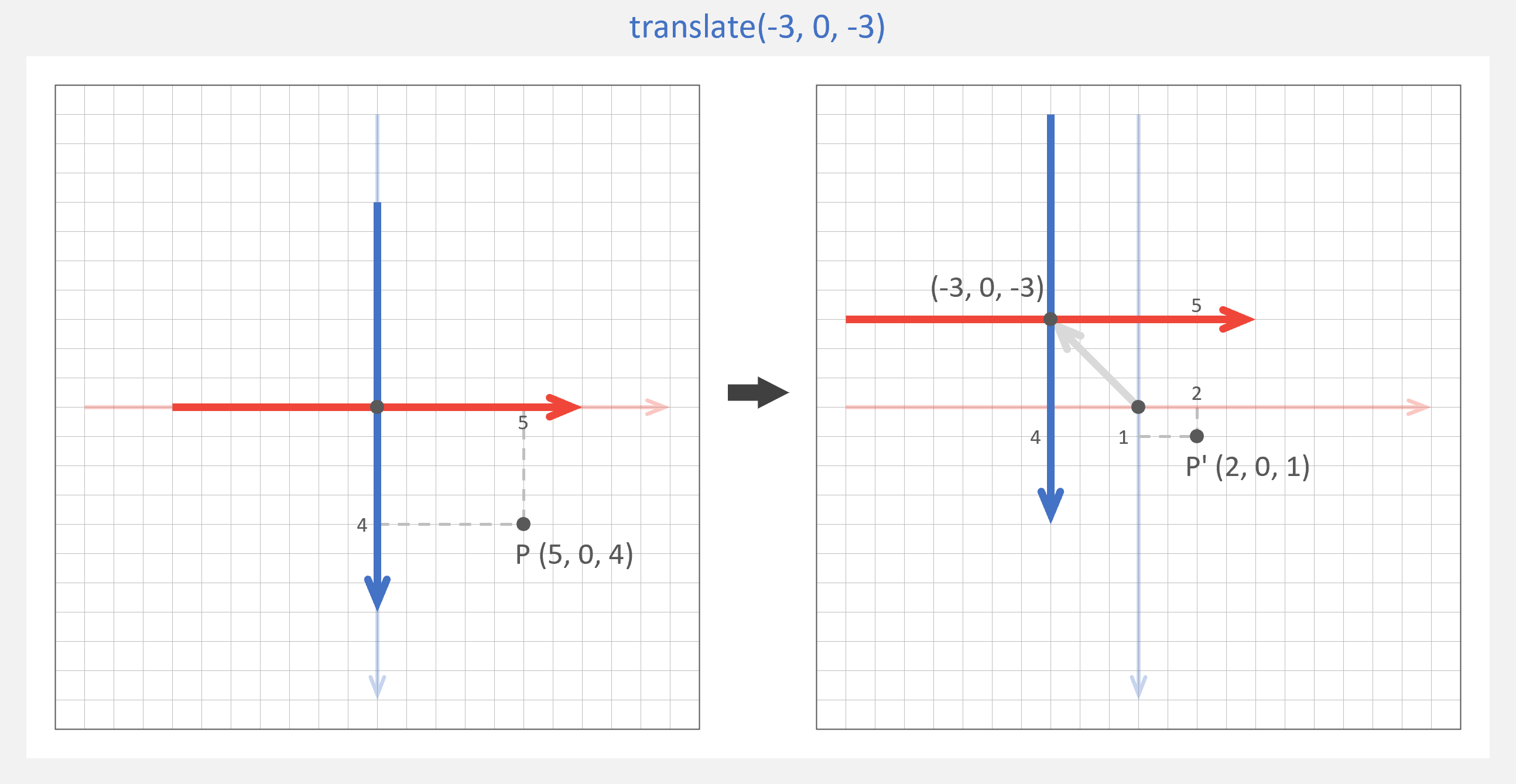
マスター「また、同様に rotateY( radians(30) ) の場合は」
マスター「次のように計算することができ、」
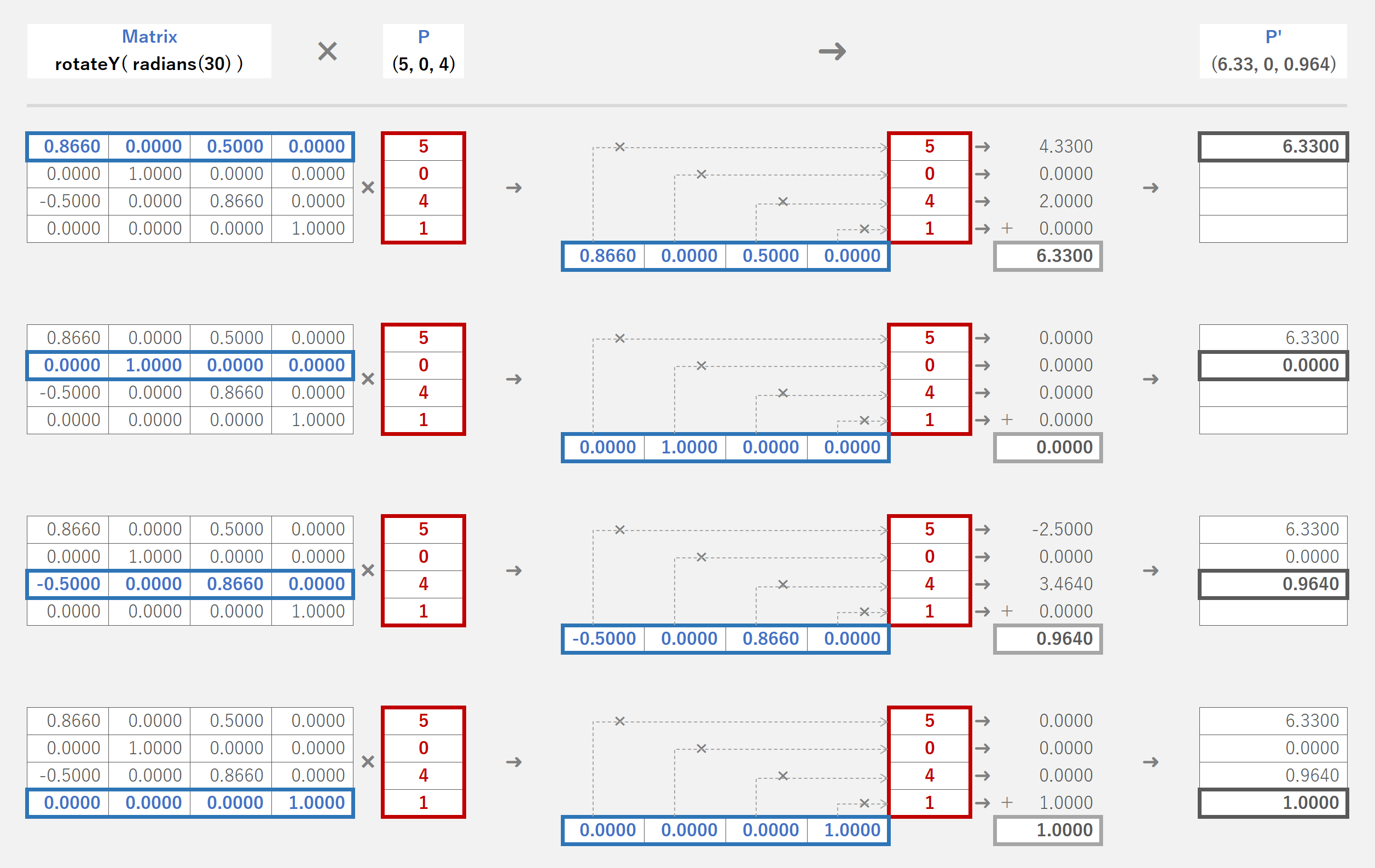
マスター「ワールド座標の 頂点 P' (6.33, 0, 0.964) に変換されるんだ」
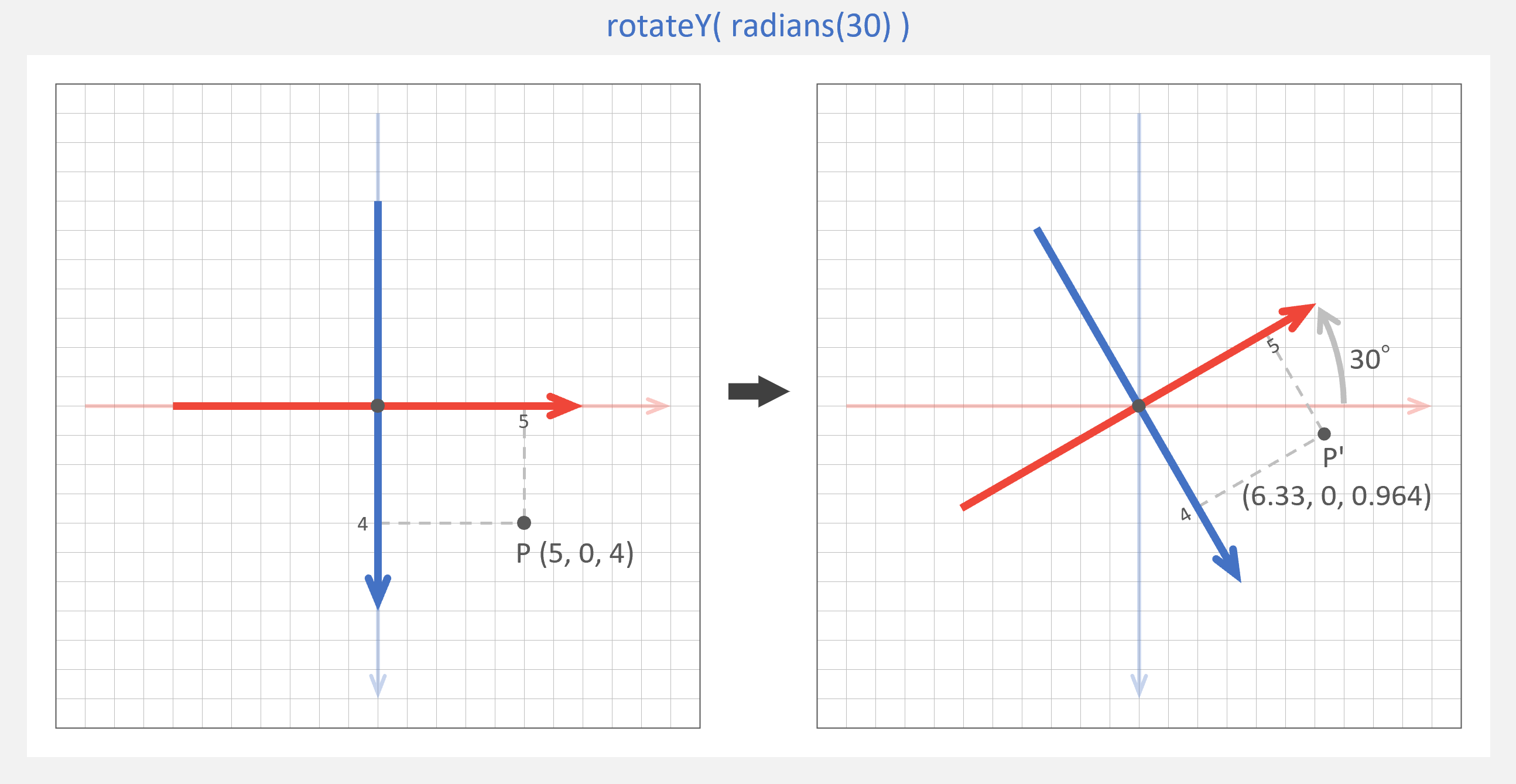
パダワン「あ!思い出した!」
パダワン「『行列』って、掛け算と足し算を鬼のように繰り返す」
パダワン「めんどっちーやつだ!!!」
パダワン「あとはバッチリ忘れた!」
アフィン変換
マスター「回転 (rotate)は、線形変換と呼ばれる変換の一種で、」
マスター「その仲間には 拡大縮小 (scale) やせん断 (shear)があるんだ」
パダワン「せん断???」
マスター「騎士アメ (脚注:金太郎飴)を斜めにカットした時の」
マスター「断面を思い浮かべられるか?」
パダワン「あ!おじさんがカットをミスったときの、」
パダワン「あのダサい顔のヤツ!(笑)」
マスター「あれがせん断だと思えばいい」
マスター「だが、拡大縮小とせん断は今回はやらないぞ」
マスター「興味があれば自分で勉強するんだ」
マスター「そして、」
マスター「線形変換に平行移動 (translate) を加えたものを」
マスター「アフィン変換 と言うんだ」
パダワン「ふーん …」
マスター「そして、このアフィン変換は」
マスター「4 次正方行列で表現することができ、」
マスター「各変換と関連する行列の成分は以下のとおりだ」
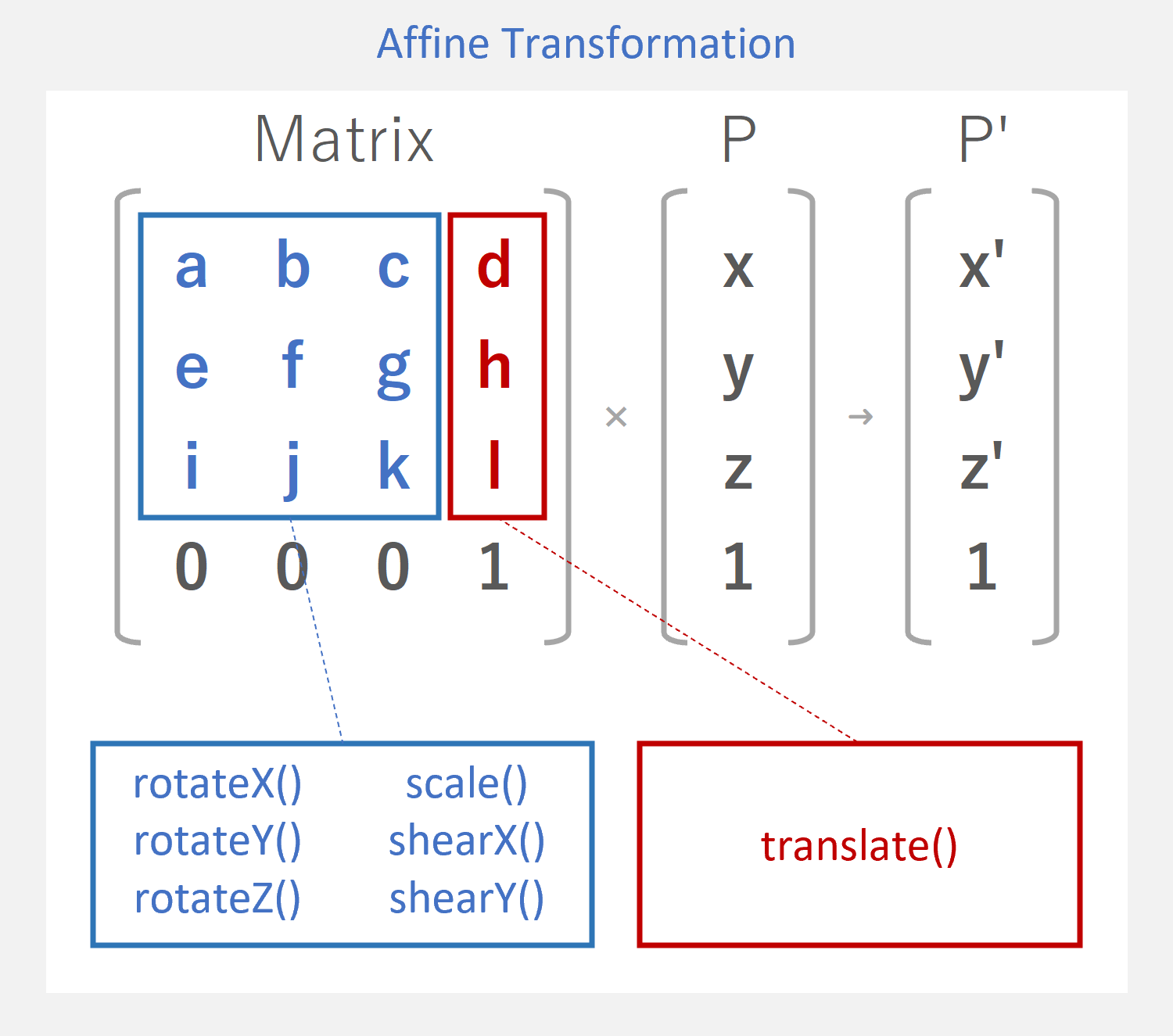
マスター「また、並行移動と回転に関する」
マスター「メソッドとマトリクスの対応は以下のとおりだ」
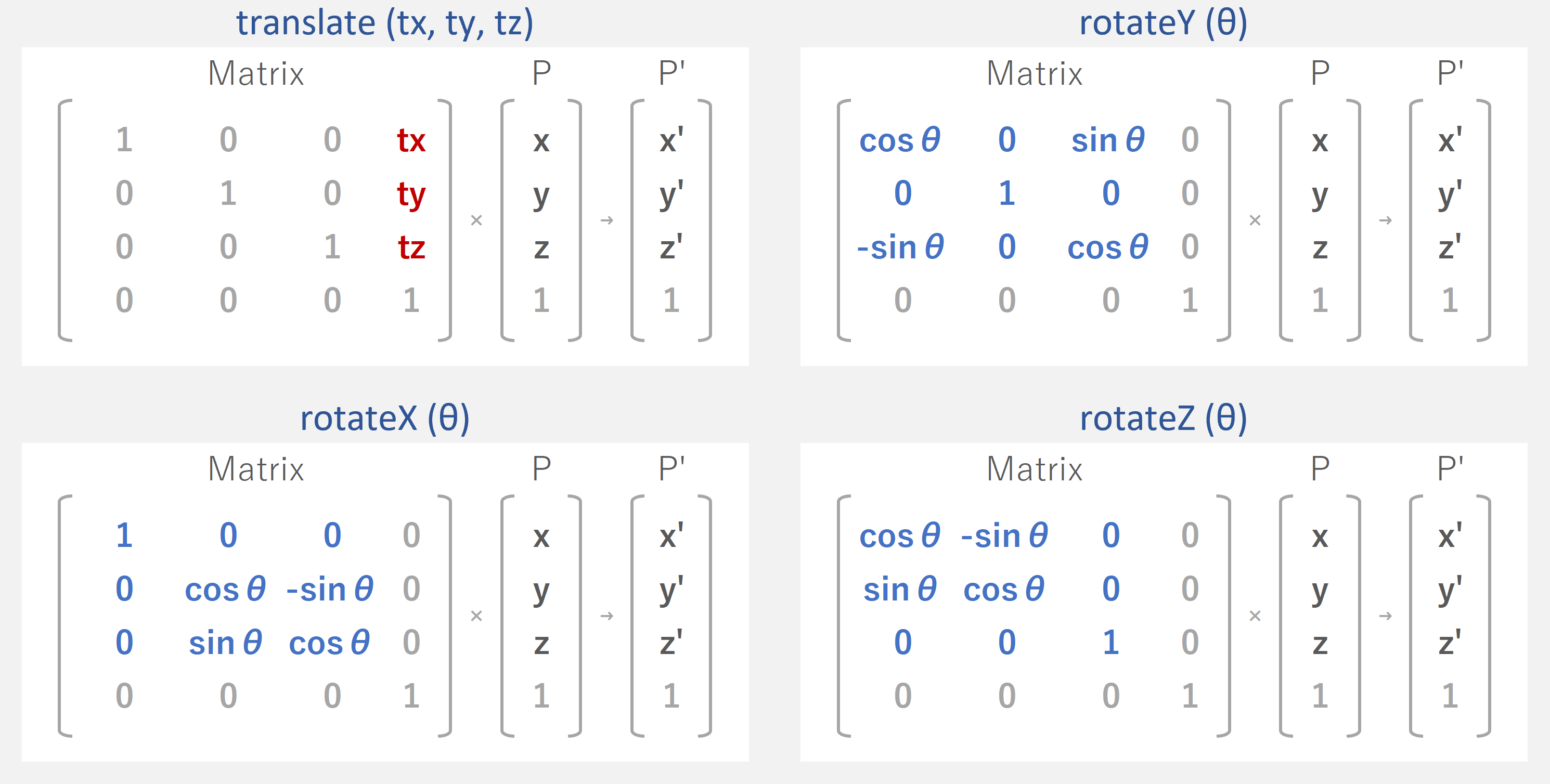
マスター「ちなみに、イニシエイト時代に」
マスター「2 次平面 (XY 平面) 上の任意の点 P (x, y) を」
マスター「原点 (0, 0) を中心に角度 θ だけ回転させた」
マスター「点 P' (x', y') を求める式を習ったと思うが、、」
マスター「覚えてるか?」
x' = x cosθ - y sinθ
y' = x sinθ + y cosθ
パダワン「うん!」
パダワン「もちろん、覚えてない!!!」
マスター「例えば、30°回転の場合は以下のように計算したはずだ」
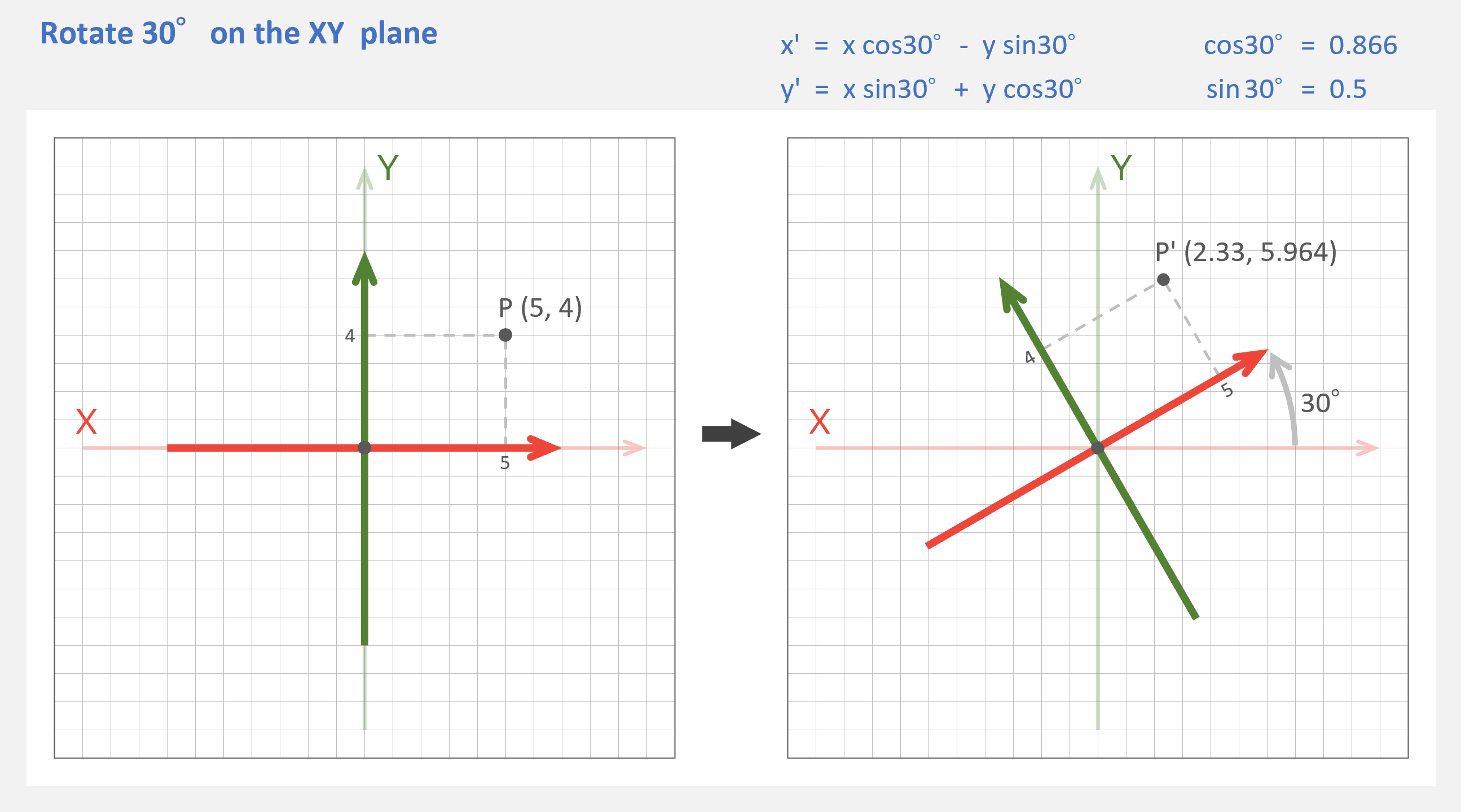
マスター「Z 軸まわりの回転 rotateZ() のマトリクスを計算すると」
マスター「上式と一致することがわかるだろう」
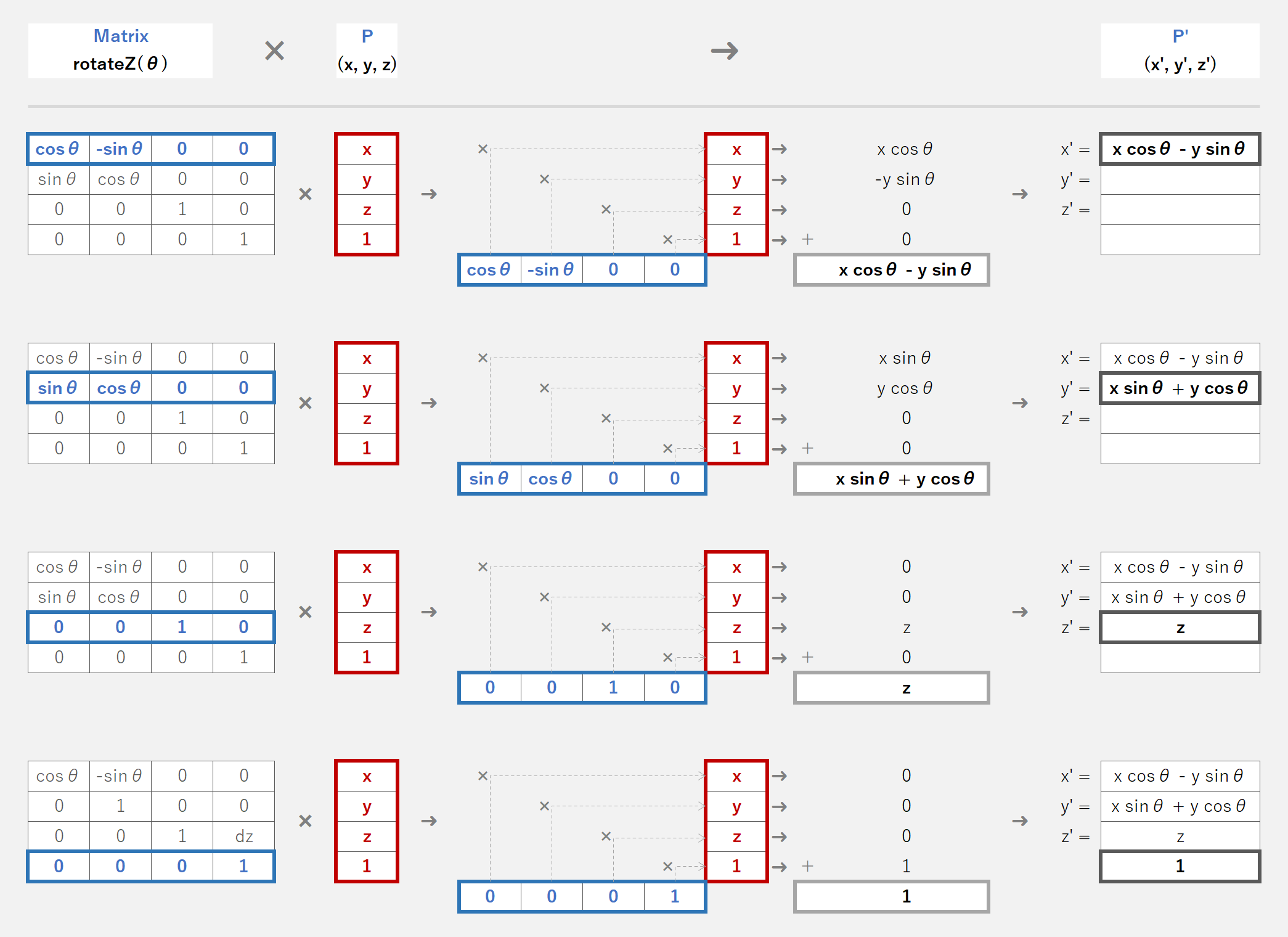
パダワン「一致することは分かったけど、、」
パダワン「えーと、何かが変 …」
パダワン「あっ!さっきのと矢印の向きが違うのに」
パダワン「なんで回る向きは一緒なの???」
パダワンは、頭の中で ZX 平面の図と XY平面の図を比べていた。
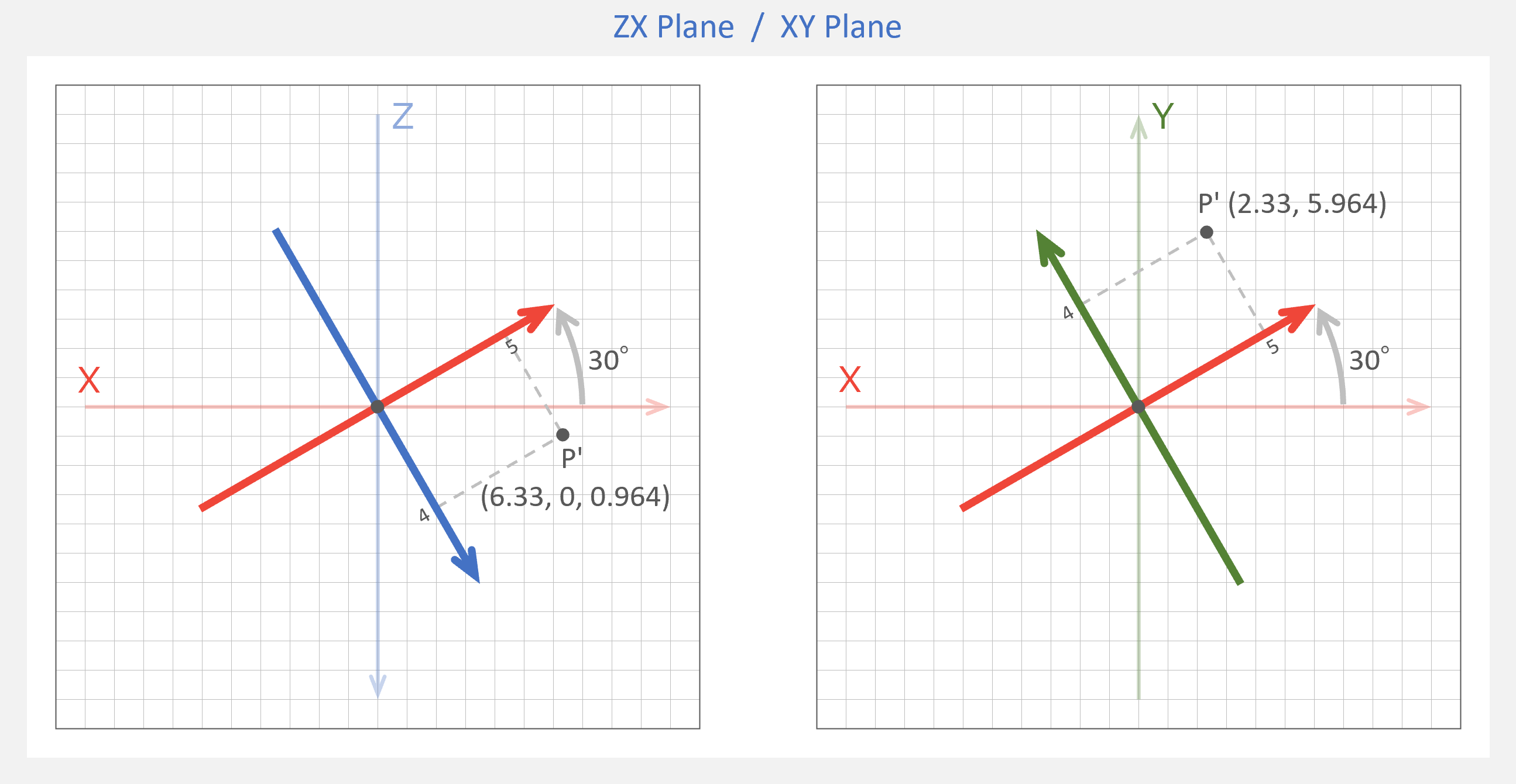
パダワン「矢印が逆だから、、」
パダワン「えーと、裏返すと、回る向きが逆になるはず …」
パダワン「えーと、、あれれ???」
パダワン「頭こんがらがった(笑)」
マスター「パダワンよ …」
パダワン(うぅっ、怒られるのか …)
Rotate (回転) の向き
マスター「いいところに気が付いたな!」
パダワン「へ?」
マスター「縦軸と横軸に何を置くか、」
マスター「ライトサイド(正の無限大方向)がどちら向きか、」
マスター「それによって回転の方向が変わってくるから」
マスター「それらを揃えて見てみるんだ」
マスター「Processing はデフォルトで縦軸が下向き、横軸が右向きだから」
マスター「各平面をそれに合わせて見てみよう」
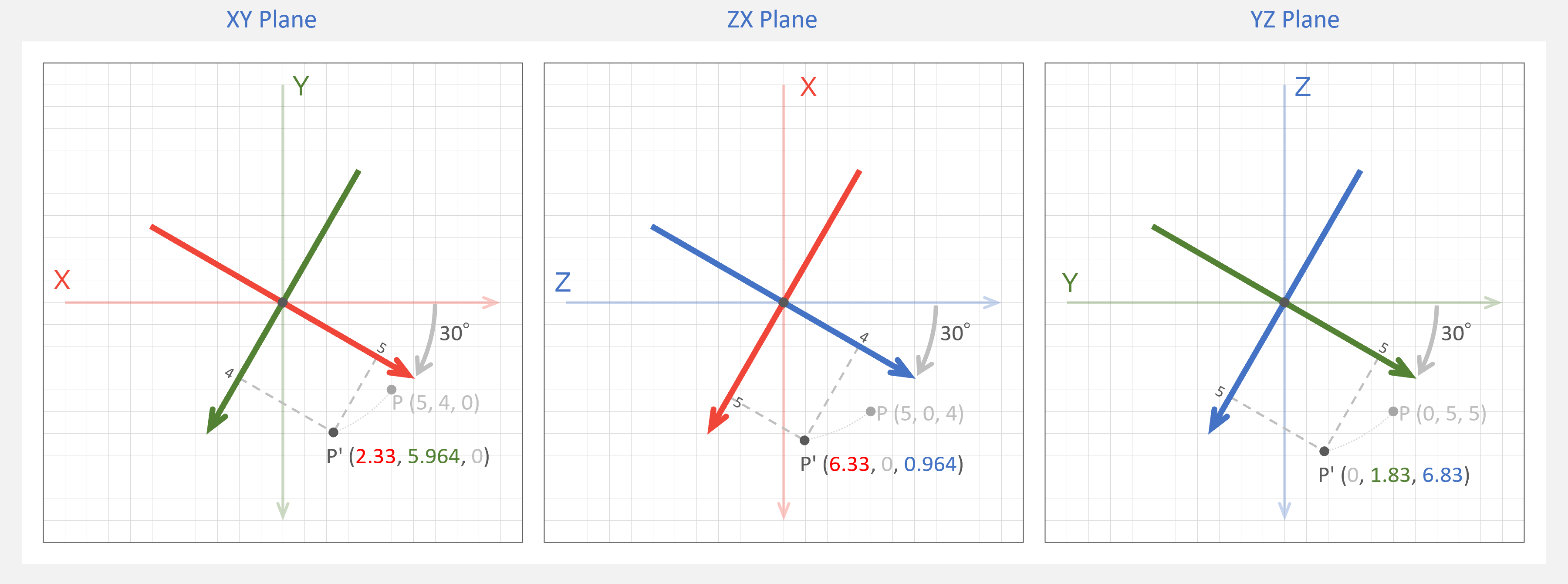
マスター「そうすると、回転の向きは次のようにすべて時計回りになるんだ」
パダワン「あ、ずりぃ!」
パダワン「X が縦になってる!」
マスター「そう。ZX 平面を XY 平面と同じ視点で見るには」
マスター「X を縦軸に、Z を横軸にする必要があるんだ」
マスター「これまでの ZX 平面の図は」
マスター「その方がイメージが掴みやすいだろうと思い」
マスター「X を横軸にしていたんだ」
マスター「Processing が左手系であることを思い出すんだ」
マスター「例えば ZX 平面であれば、」
マスター「人差し指 (Y 軸) を自分の方に向けてから」
マスター「残りの指が右と下を向くようにすると、」
マスター「親指 (X 軸) と中指 (Z 軸) の向きが自然に定まり」
マスター「この図と一致することがわかるだろう」
パダワン「あ、ほんとだ …」
パダワン「親指が下で中指が右だ!」
マスター「そして、」
マスター「rotateX() rotateY() rotateZ() の処理をよく見てみると」
マスター「sin (正弦) が縦軸の成分、cos (余弦) が横軸の成分として」
マスター「計算されていることがわかるだろう」
メソッド|回転軸|影響を
受ける
平面|平面の
横軸|平面の
縦軸|cosθ
(余弦)|sinθ
(正弦)
:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:
rotateZ()|Z 軸|XY 平面|X 軸|Y 軸|X 成分|Y 成分
rotateY()|Y 軸|ZX 平面|Z 軸|X 軸|Z 成分|X 成分
rotateX()|X 軸|YZ 平面|Y 軸|Z 軸|Y 成分|Z 成分
マスター「cosθ が X 成分で、sinθ が Y 成分と覚えてしまうと」
マスター「ZX 平面や YZ 平面で混乱してしまうだろうから、」
マスター「cosθ は横軸成分(幅)で、sinθ が縦軸成分(高さ)と覚えるんだ」
マスター「また、回転の式を整理すると以下のとおりになる」
| メソッド | 回転軸 | 影響を 受ける 平面 |
回転の式 |
|---|---|---|---|
| rotateZ() | Z 軸 | XY 平面 | x' = x cosθ - y sinθ y' = x sinθ + y cosθ |
| rotateY() | Y 軸 | ZX 平面 | z' = z cosθ - x sinθ x' = z sinθ + x cosθ |
| rotateX() | X 軸 | YZ 平面 | y' = y cosθ - z sinθ z' = y sinθ + z cosθ |
パダワン「あ、頭が、、」
パダワン「爆発しそー!!!」
マスター「がはは」
マスター「まあ、式を覚える必要はない」
マスター「変換メソッドがマトリクスを計算してくれるからな」
マスター「ただ、各軸の回転の向きは頭に入れておいた方が良い」
マスター「回転軸を自分に向けた場合、」
マスター「その軸が回転する正の方向は時計回りだ」
マスター「例えば rotateZ() に正数を渡した場合は、」
マスター「Z 軸を自分に向ければ XY 平面は時計回りに回るんだ」
マスター「そして、もちろん rotateZ() に負数を渡した場合は、」
マスター「言うまでもなく反時計回りだ」
マスター「各軸の回転の『正の方向』は次のとおりだ」
マスター「これを体に染み込ませるんだ」
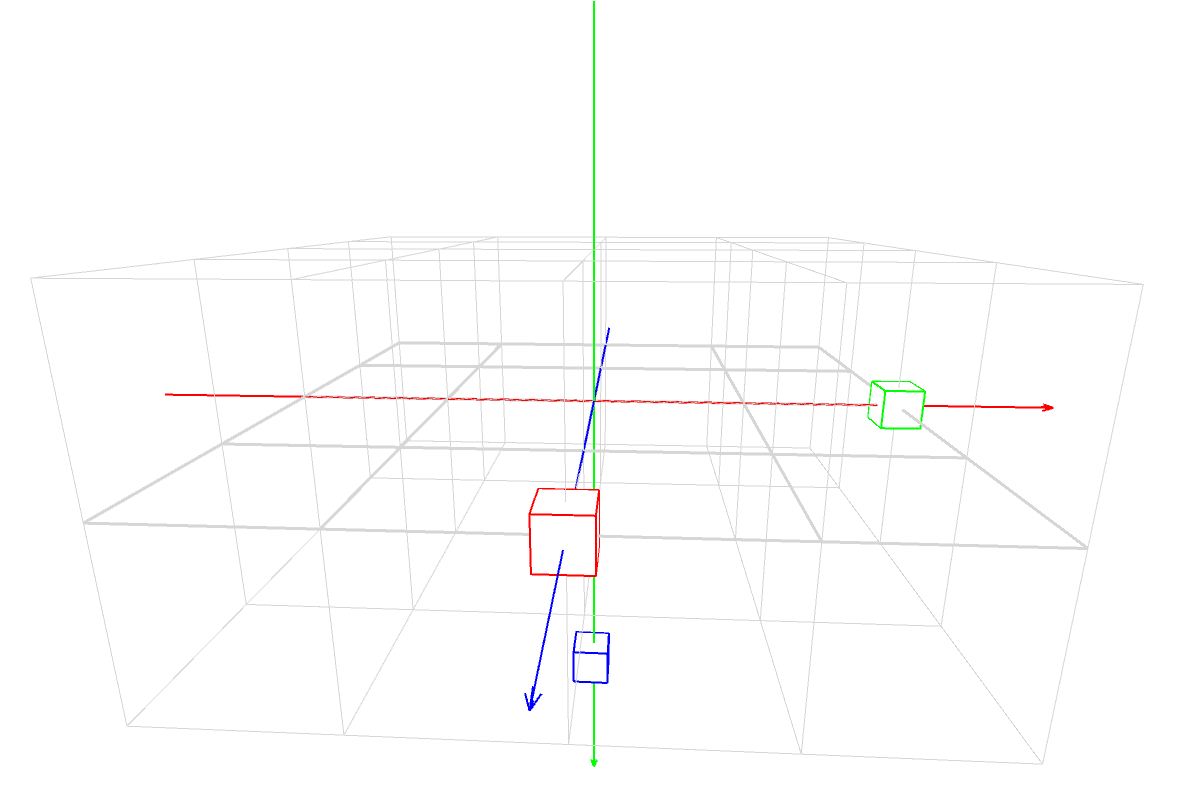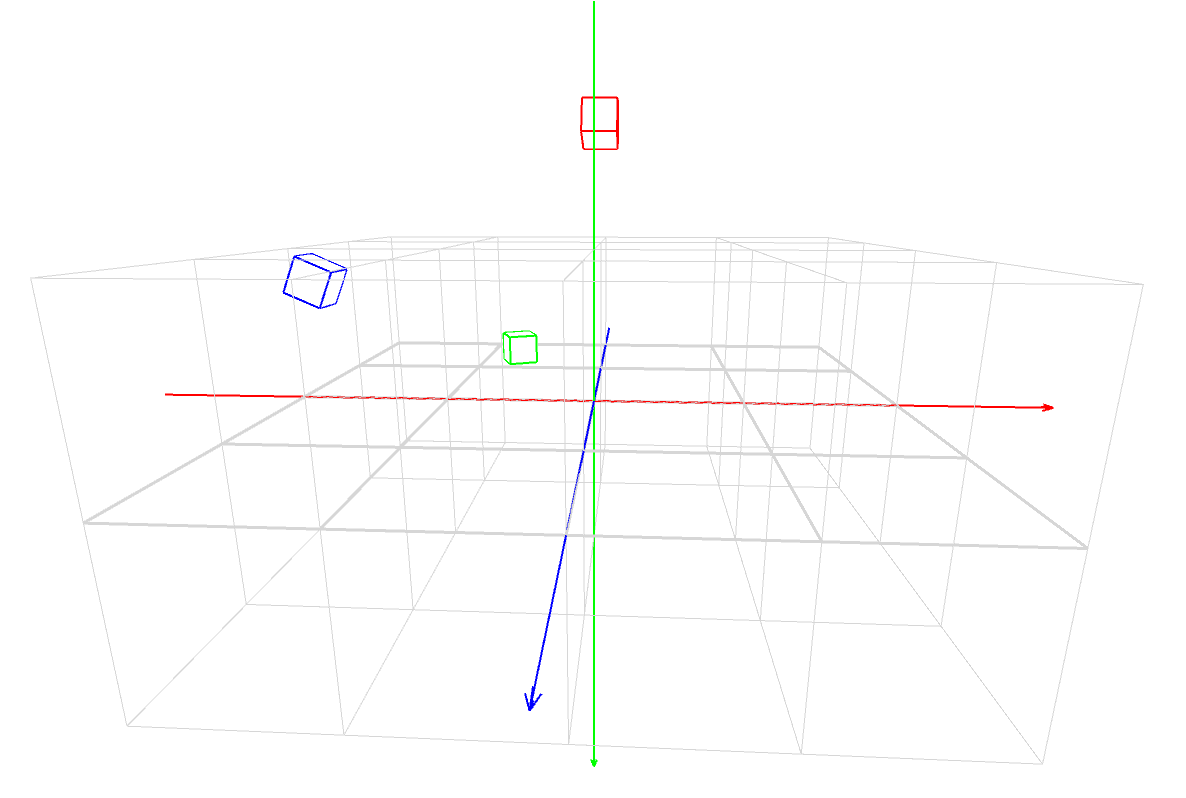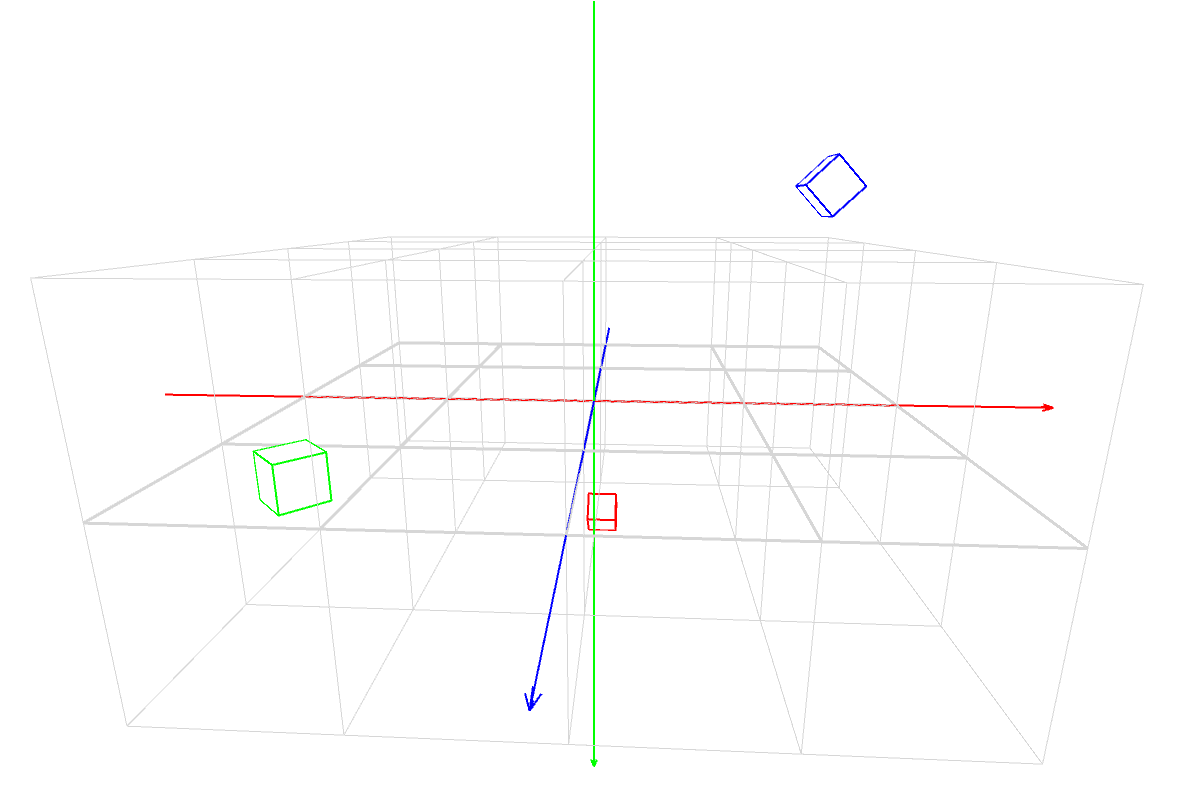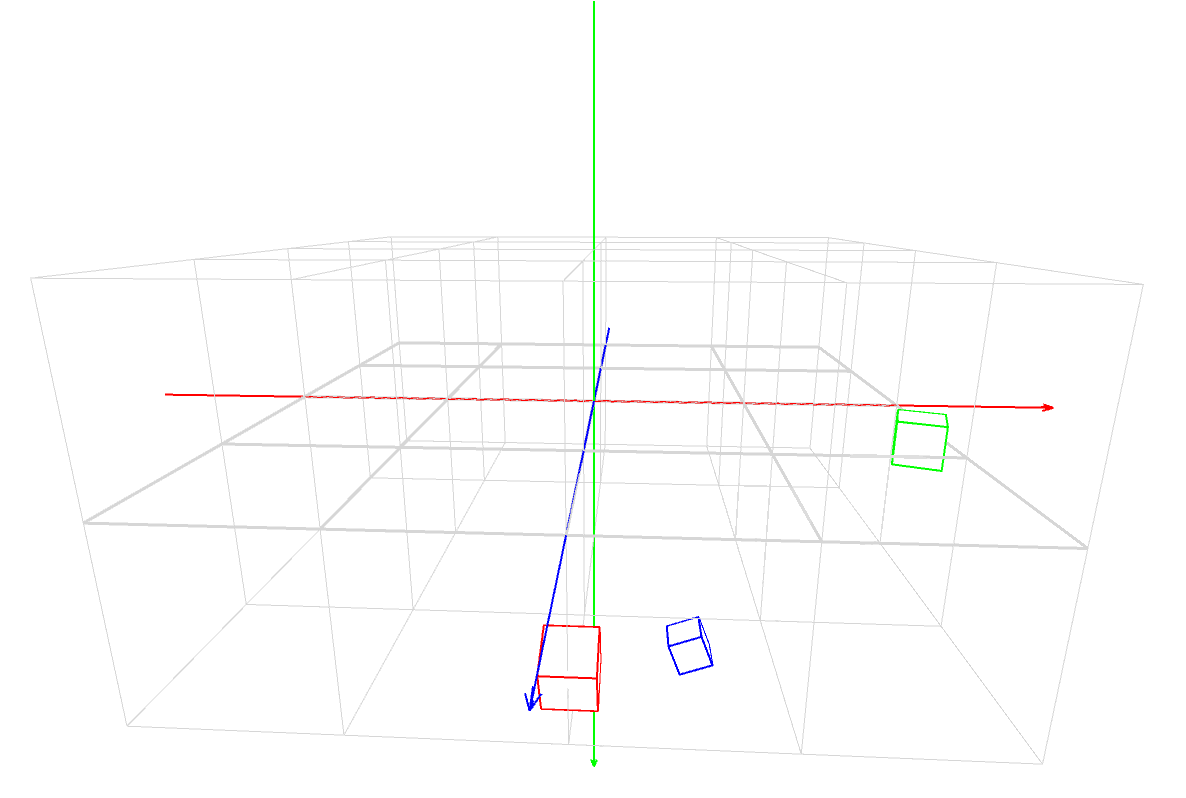
合成変換
マスター「次は、座標変換を組み合わせた場合に」
マスター「マトリクスがどうなっているかを考えてみよう」
マスター「例えば、rotateY() の後に translate() を行ったときも、」
マスター「その両方を組み合わせた変換を 1 つのマトリクスで表現できるんだ」
パダワン「2 つ分しかできないの?」
マスター「いや、変換をいくつ重ねても 1 つのマトリクスで表現できるぞ」
マスター「そして、それをオブジェクトに適用すれば、」
マスター「1 回で変換が完了するんだ」
パダワン「あっ! お小遣い帳と一緒だ!」
マスター「は???」
パダワン「お小遣い帳もさぁ、、」
パダワン「お買い物をいくつ重ねても」
パダワン「その月の『収支』を 1 つの数字で表現できるよ!」
パダワン「で、その収支を、先月末の残高に足すだけで」
パダワン「今月の残高が計算できるでしょ!」
| 座標変換 | お小遣い帳 |
|---|---|
| translate() | 小遣い 10 credit |
| rotateY() | あめ -1 credit |
| translate() | 騎士フィギュア -6 credit |
| rotateZ() | ガム -1 credit |
| rotateX() | 子供セーバー -4 credit |
| 合成マトリクス | 今月の収支 -2 credit |
マスター「今月は赤字のようだな(笑)」
マスター「まあ、そう考えてもいいだろう」
マスター「だが、座標変換の場合は加算じゃなくて乗算だ」
マスター「しかも、各変換は 4 次正方行列だから、」
マスター「4 次正方行列どうしの乗算になるんだ」
マスター「さっき新しく作ったスケッチに以下を追記するんだ」
...
// 合成変換の確認 // これ以降を追記
println("----------------------------------");
resetMatrix();
rotateY(radians(30)); println("rotateY(radians(30));");
printMatrix();
resetMatrix();
rotateX(radians(30)); println("rotateX(radians(30));");
printMatrix();
マスター「コンソールに出力された RotateY() と RotateX() の」
マスター「2 つの変換行列を乗じてみよう」
----------------------------------
rotateY(radians(30));
0.8660 0.0000 0.5000 0.0000
0.0000 1.0000 0.0000 0.0000
-0.5000 0.0000 0.8660 0.0000
0.0000 0.0000 0.0000 1.0000
rotateX(radians(30));
1.0000 0.0000 0.0000 0.0000
0.0000 0.8660 -0.5000 0.0000
0.0000 0.5000 0.8660 0.0000
0.0000 0.0000 0.0000 1.0000
マスター「計算の方法は次のとおりだ」
マスター「まずは 1 行目を次のように計算し、」
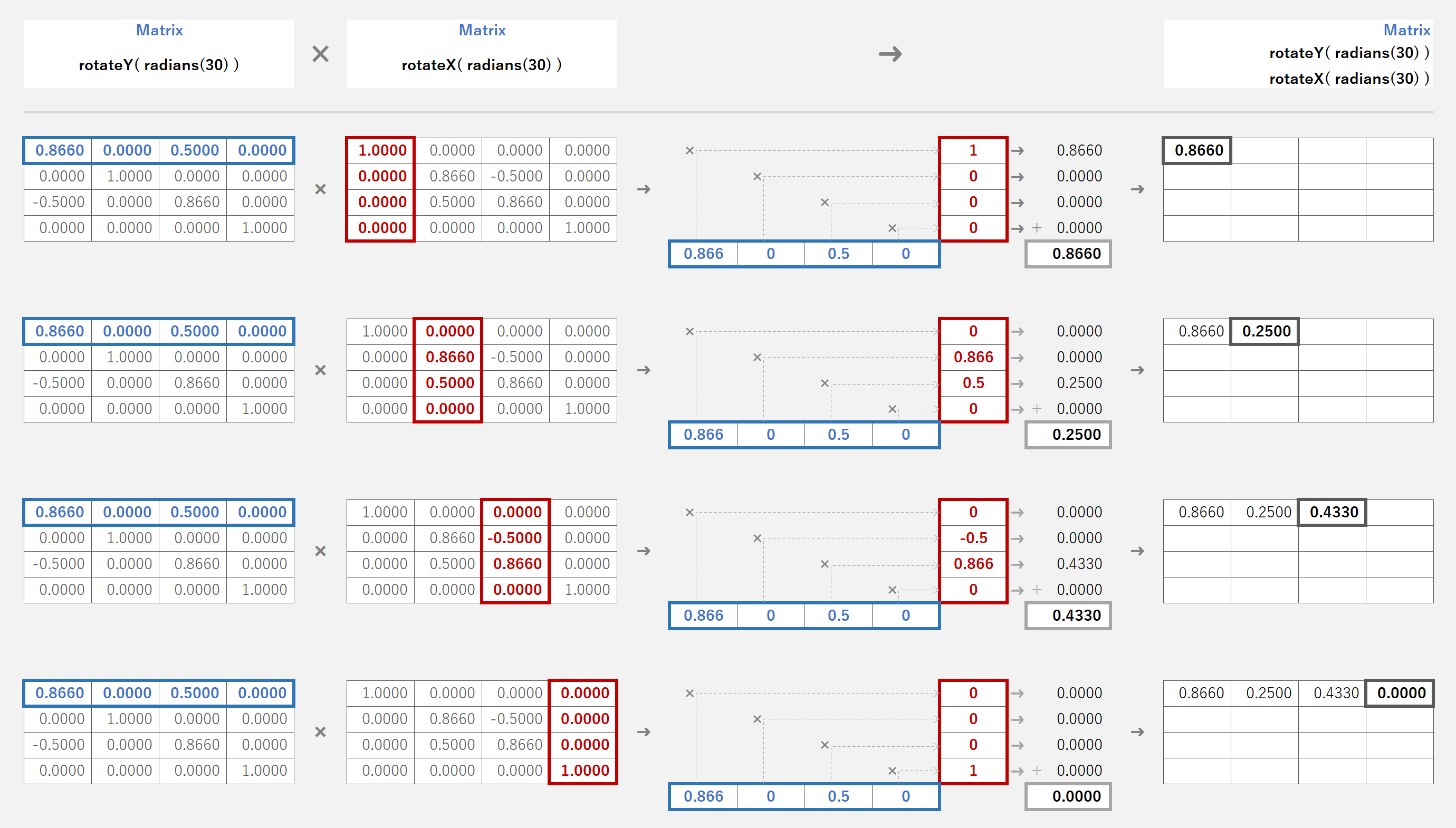
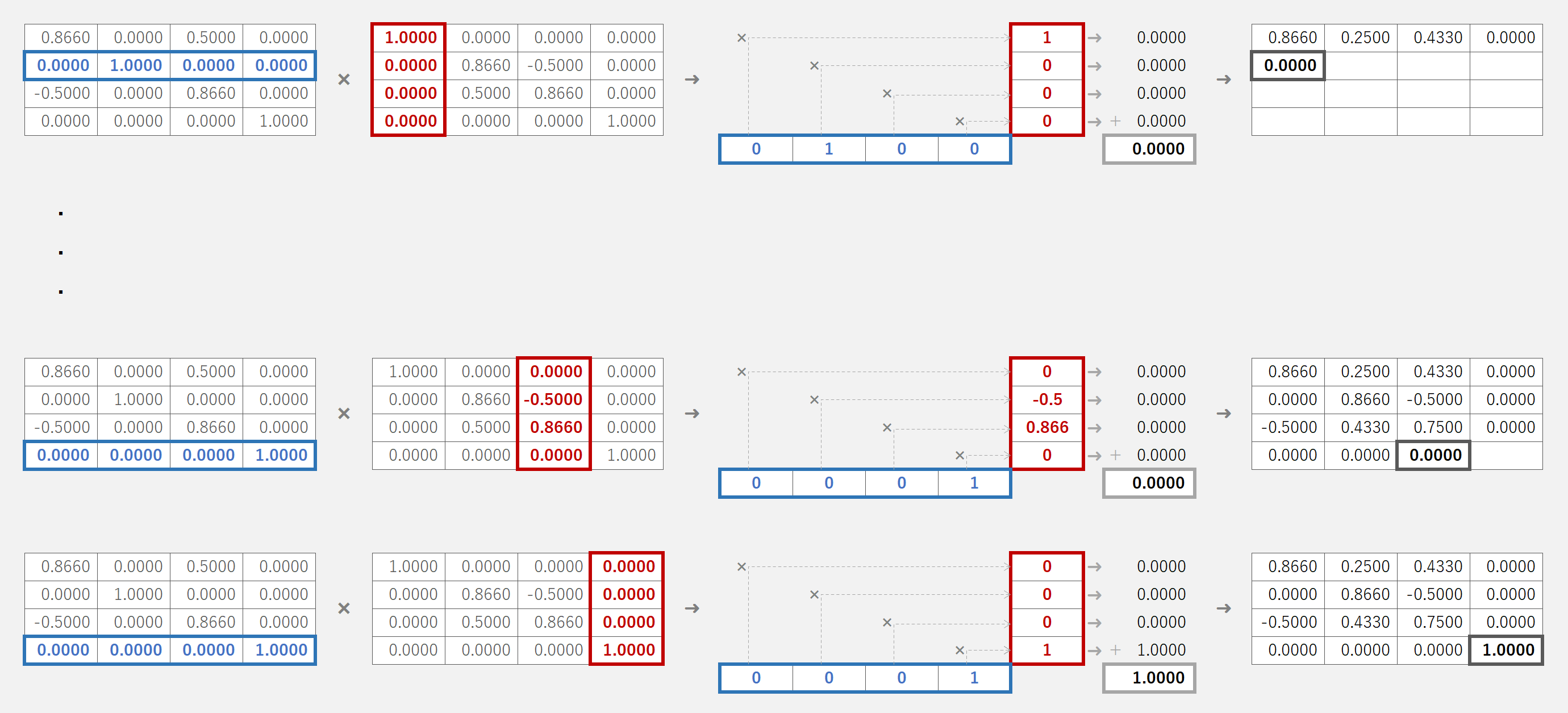
マスター「2 行目以降も同じように計算すれば良い」
パダワン「うあああー!」
パダワン「めんどくせー!!!」
マスター「スケッチに以下を追記し、」
マスター「計算結果が合っているかどうか確認するんだ」
...
resetMatrix(); // これ以降を追記
rotateY(radians(30)); println("rotateY(radians(30));");
rotateX(radians(30)); println("rotateX(radians(30));");
printMatrix();
rotateY(radians(30));
rotateX(radians(30));
0.8660 0.2500 0.4330 0.0000
0.0000 0.8660 -0.5000 0.0000
-0.5000 0.4330 0.7500 0.0000
0.0000 0.0000 0.0000 1.0000
パダワン「おお!合ってる!!!」
パダワン「てか、これセーバー書いた方が早くね?!」
マスター「書いてみるか!?」
マスター「現在のマトリクスを得る方法は」
マスター「さっき turnToCamera() でやったから分かるな?」
マスター「取得した PMatrix インスタンスのメソッド get() に、」
マスター「要素数 16 の float 配列(1次元配列)を渡すと」
マスター「マトリクスを配列で取得できるぞ」
パダワン「えーと、、」
パダワンは Matrix.pde に以下を追記した。
...
// マトリクス同士の乗算 // これ以降を追記
println("----------------------------------");
float[] m1 = new float[16]; // rotateY() の結果
float[] m2 = new float[16]; // rotateX() の結果
float[] m3 = new float[16]; // rotateY() と rotateX() の合成結果
resetMatrix();
rotateY(radians(30));
((PMatrix3D)g.getMatrix()).get(m1);
resetMatrix();
rotateX(radians(30));
((PMatrix3D)g.getMatrix()).get(m2);
for (int i = 0; i < 4; i++)
for (int j = 0; j < 4; j++)
for (int k = 0; k < 4; k++)
m3[i * 4 + j] += m1[i * 4 + k] * m2[k * 4 + j];
println(m3);
パダワン「ふぅ、これで合ってるかな …」
----------------------------------
[0] 0.8660254
[1] 0.25
[2] 0.4330127
[3] 0.0
[4] 0.0
[5] 0.8660254
[6] -0.5
[7] 0.0
[8] -0.5
[9] 0.4330127
[10] 0.75
[11] 0.0
[12] 0.0
[13] 0.0
[14] 0.0
[15] 1.0
パダワン「うん!合ってるみたい!」
パダワン「てか、これって Processing が計算してくれんのに」
パダワン「自分で書く意味あんの???」
マスター「ない(笑)」
パダワン「げっ!また騙された!!!」
パダワン「なんだよ!チクショー!」
マスター「まあ。そう荒れるな(笑)」
マスター「ライブラリの挙動が」
マスター「自分の想定と合っているかどうかを確認したいことも」
マスター「今後きっと出てくるはずだ」
マスター「その時のための練習だと思っておくのだな」
3 時 30 分|カメラの正体
マスター「そうしたら Matrix.pde に以下を追記するんだ」
...
// カメラの挙動 // これ以降を追記
println("----------------------------------");
camera(50, 0, 100, 50, 0, 0, 0, 1, 0);
println("camera(50, 0, 100, 50, 0, 0, 0, 1, 0);");
printMatrix();
camera(0, 0, 0, 250, 0, -433, 0, 1, 0);
println("camera(0, 0, 0, 250, 0, -433, 0, 1, 0);");
printMatrix();
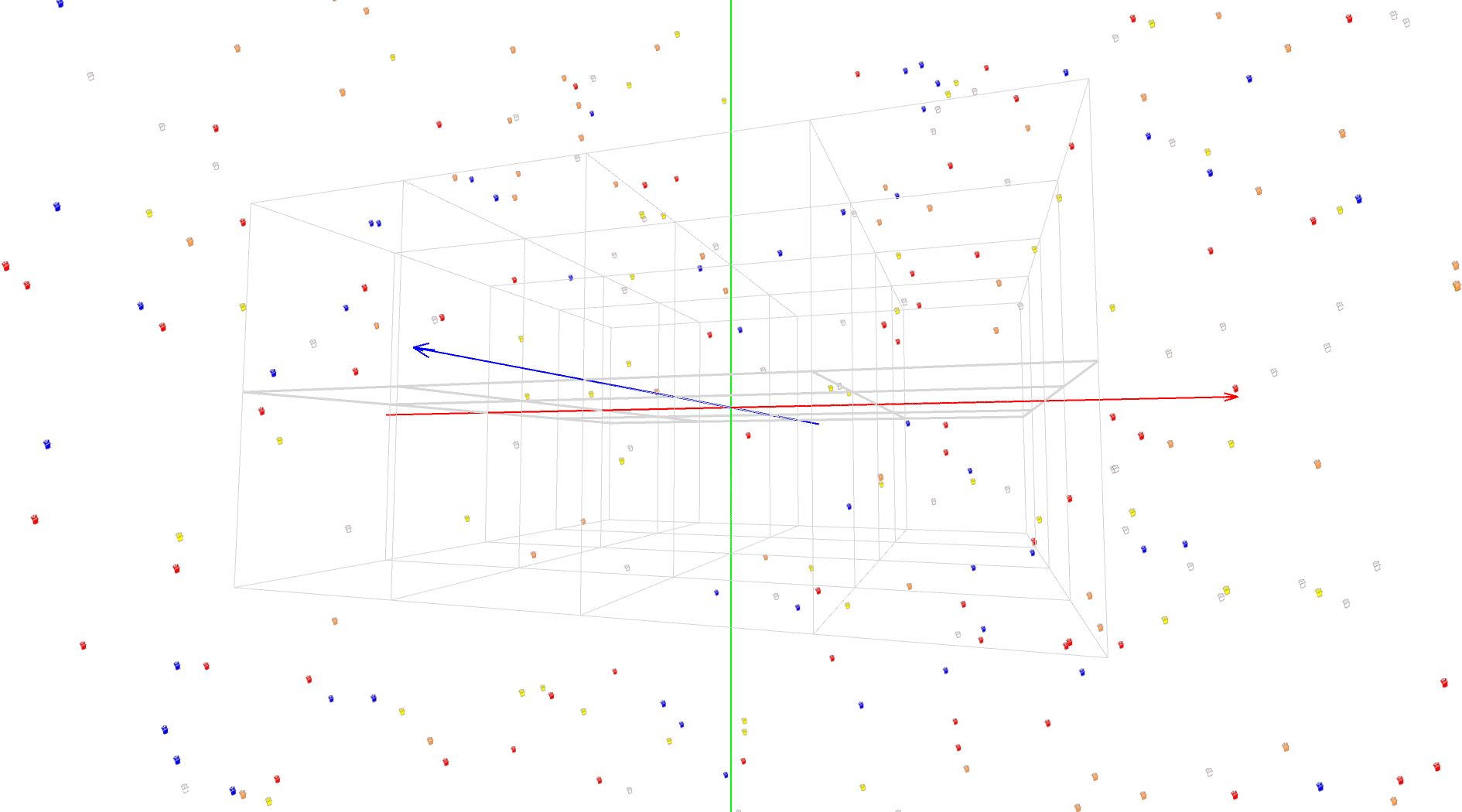
マスター「上記では、ワールド座標系にカメラを配置し(下図)、」
マスター「その直後にマトリクスを確認している」
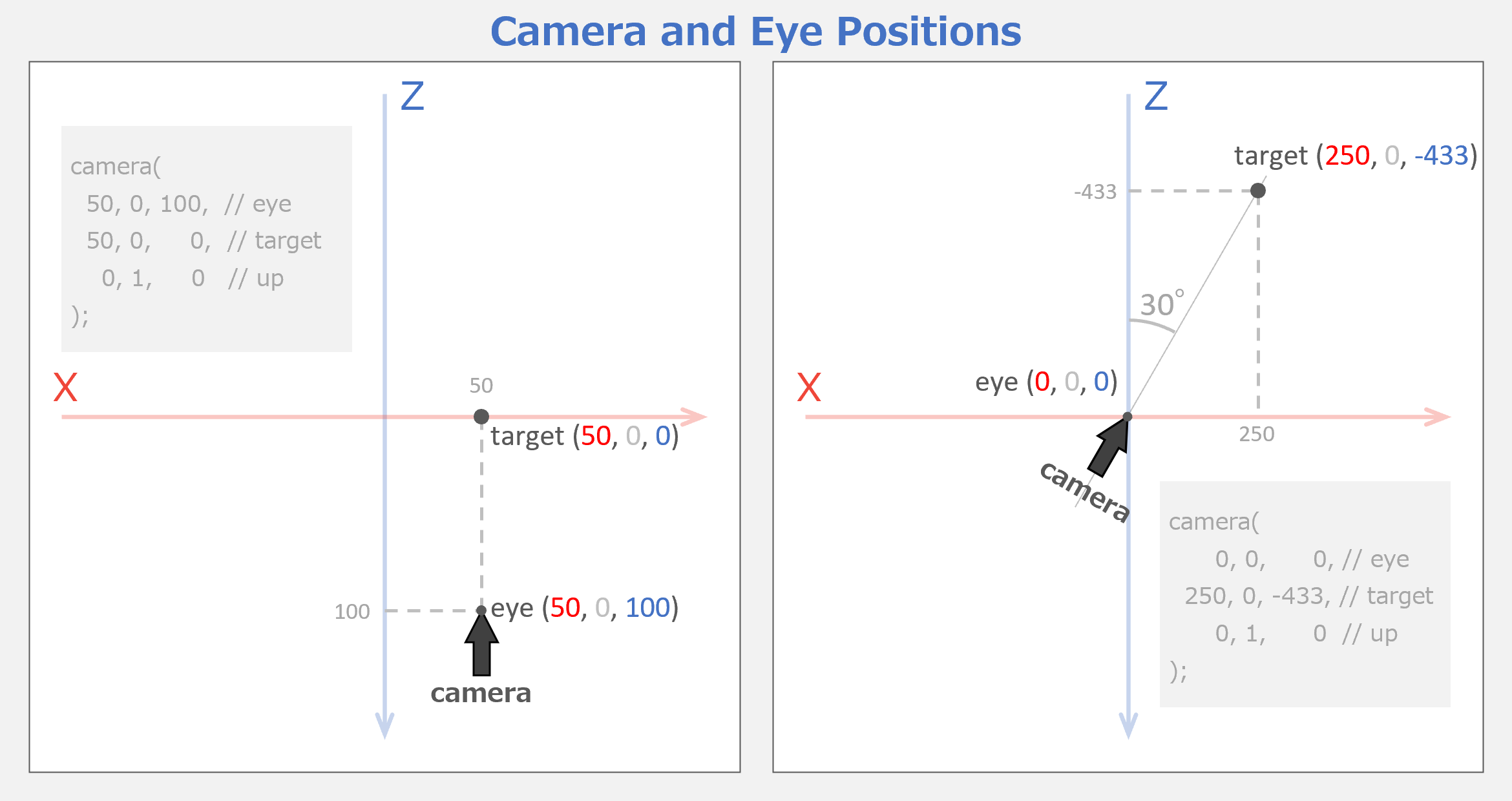
マスター「分かりやすくするために」
マスター「カメラもターゲットも ZX 平面上に配置している」
マスター「そして、左は、視線を Z 軸と平行にし、」
マスター「右は、視線を Z 軸から 30° 傾けている」
パダワン「でも、なんでマトリクスを確認すんの?」
パダワン「あっ!」
----------------------------------
camera(50, 0, 100, 50, 0, 0, 0, 1, 0);
001.0000 000.0000 000.0000 -050.0000
000.0000 001.0000 000.0000 000.0000
000.0000 000.0000 001.0000 -100.0000
000.0000 000.0000 000.0000 001.0000
camera(0, 0, 0, 250, 0, -433, 0, 1, 0);
0.8660 -0.0000 0.5000 0.0000
0.0000 1.0000 0.0000 0.0000
-0.5000 0.0000 0.8660 0.0000
0.0000 0.0000 0.0000 1.0000
パダワン「なんか見覚えのある数が並んでる!」
パダワン「でも、-0.0000 って何だ?」
マスター「それは 銀河標準化機関が第 754 号として定めた」
マスター「浮動小数点数に関する規格(脚注:IEEE754 のこと)に絡む話で、」
マスター「ひとまず今は、通常の 0 と同じだと考えれば良い」
マスター「それ以外はどうだ?」
パダワン「うん。0.866 とか 0.5 とかは、」
パダワン「さっきの鬼みたいな足し算と掛け算の繰り返しで」
パダワン「いっぱい見た数字だよ」
マスター「そうだな」
マスター「では、それを確かめるために次を入力してみよう」
...
// 座標変換との比較 // これ以降を追記
println("----------------------------------");
resetMatrix();
translate(-50, 0, -100);
println("translate(-50, 0, -100);");
printMatrix();
resetMatrix();
rotateY(radians(30));
println("rotateY(radians(30));");
printMatrix();
パダワンが [実行] ボタンをクリックすると、コンソールに以下が出力された。
----------------------------------
translate(-50, 0, -100);
001.0000 000.0000 000.0000 -050.0000
000.0000 001.0000 000.0000 000.0000
000.0000 000.0000 001.0000 -100.0000
000.0000 000.0000 000.0000 001.0000
rotateY(radians(30));
0.8660 0.0000 0.5000 0.0000
0.0000 1.0000 0.0000 0.0000
-0.5000 0.0000 0.8660 0.0000
0.0000 0.0000 0.0000 1.0000
パダワン「げげっ! 同じだ!!!」
マスター「カメラを平行移動させるということは」
マスター「オブジェクトを逆方向に移動させることと同じで、」
マスター「カメラを回転させるということは」
マスター「オブジェクトを逆方向に回転させることと、、」
パダワン「同じだ!!!」
マスター「そう。camera() というメソッドを呼び出すと」
マスター「現在のマトリクスに逆方向の変換が設定されるんだよ」
マスター「つまり、これまでワールド座標系を中心に考えてきたが」
マスター「実はカメラこそが世界の中心だったんだ」
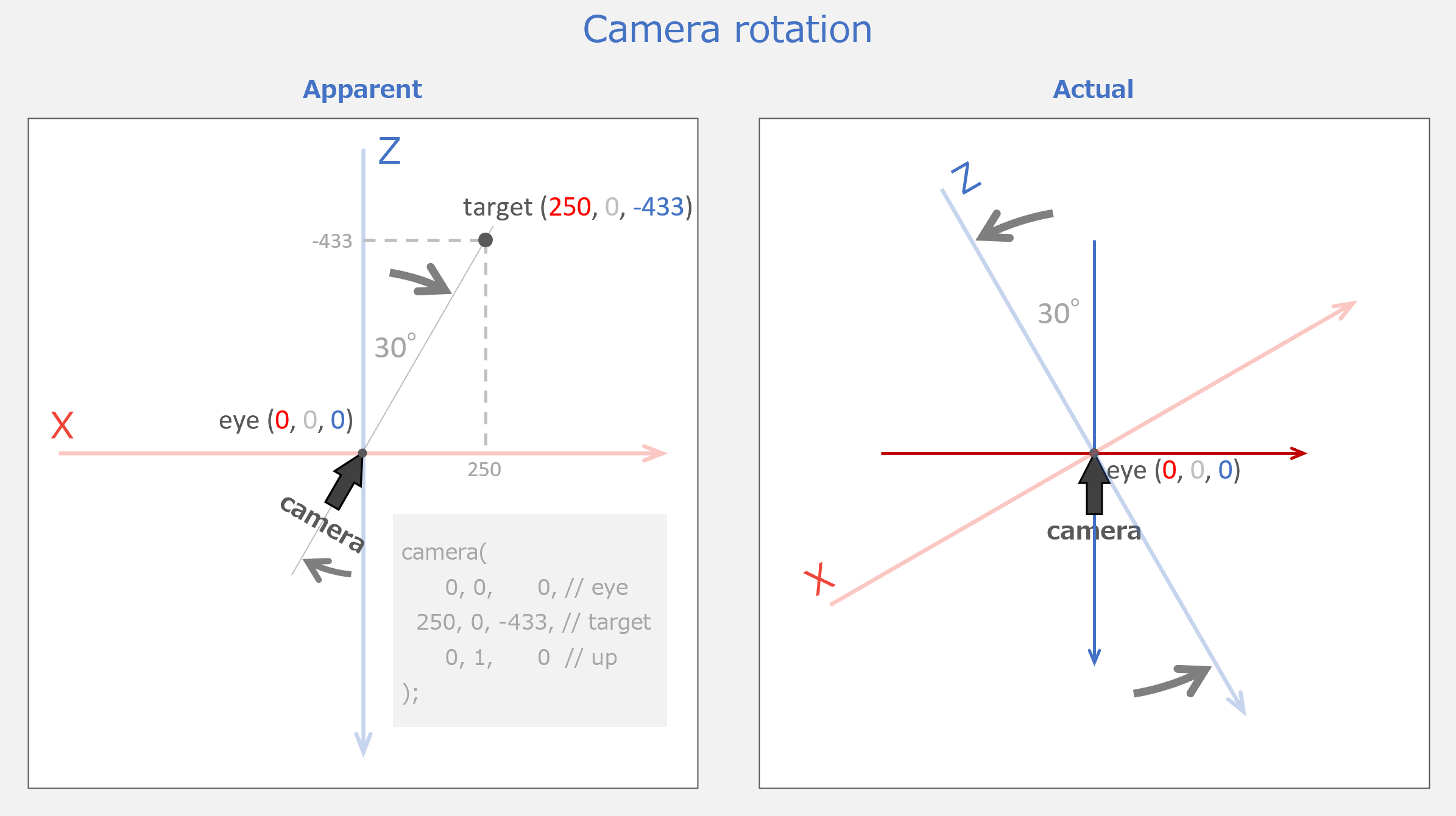
マスター「以下の図の、左側が見かけ上の動きで」
マスター「右側が実際の動きだ」
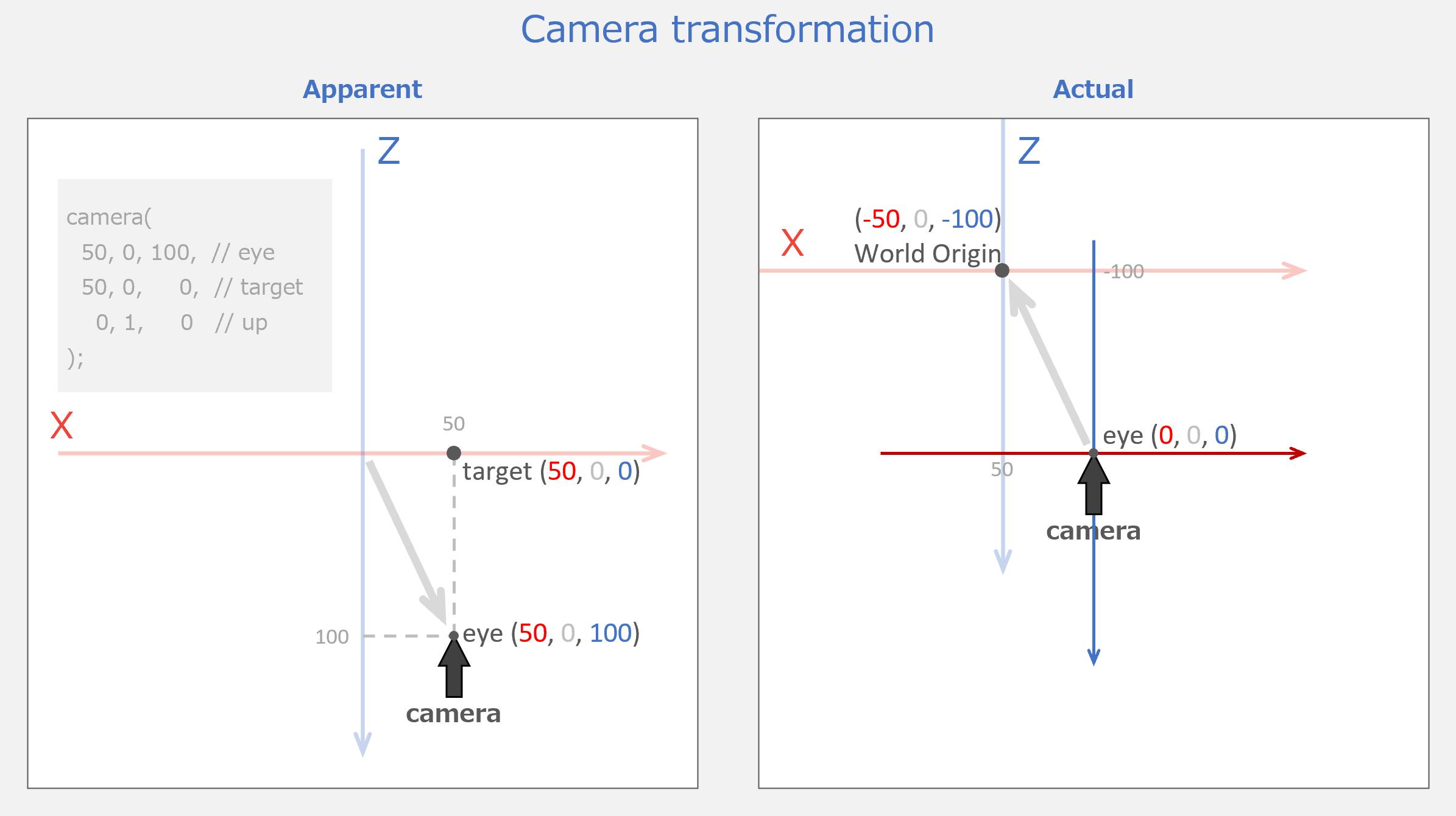
マスター「このように、camera() を呼び出すと」
マスター「世界という『舞台』が動かされた状態で戻ってくるんだ」
マスター「そして、それ以降の座標変換や描画処理は」
マスター「すべてこの舞台上で行われることになる」
マスター「また、世界という舞台を動かしても」
マスター「止まったままじっと動かない座標系のことを」
マスター「カメラ座標系 といい、」
マスター「カメラの視点は、常にその原点 (0, 0, 0) に置かれ、」
マスター「カメラは常に Z 軸のダークサイド(負の無限大方向)に」
マスター「視線を定めているんだ」
マスター「だから、カメラ座標系では、」
マスター「スクリーン平面は、常に XY 平面と平行なんだよ」
マスター「そして、camera() を呼び出すことにより実行される」
マスター「座標変換のことを ビューイング変換 というんだ」
マスター「それに対して translate() や rotateY() など、」
マスター「ローカル座標系からワールド座標系へ座標変換することを」
マスター「モデリング変換 といい、」
マスター「このふたつを合わせて モデルビュー変換 というんだ」
パダワン「ん?」
パダワン「そしたらさあ、」
パダワン「さっきの、このくだり↓↓↓↓↓、、、」
パダワン「お、なんか回ってる …」
マスター「実は、この中の物はどれも静止している」
パダワン「え??? だって回ってんじゃん!」
マスター「回っているのは、カメラなんだ」
マスター「あれは嘘だ(笑)」
パダワン「なんだよ!僕が合ってたんじゃないかー!!!」
パダワン(マスタはなんでいつもいじわるするんだ(怒))
マスター「だが、ワールド座標系を中心に据え、」
マスター「そこにオブジェクトとカメラを配置すると考えながら」
マスター「セーバーを書いてもまったく支障はないんだよ」
マスター「それがこの方法のすばらしいところさ」
ビルボードの姿勢変更の理屈
マスター「ここまで理解できれば」
マスター「さっきのビルボードの姿勢変更について説明できるぞ」
マスター「turnToCamera() をもう一度よく見てみるんだ」
...
void turnToCamera() {
PMatrix3D m = (PMatrix3D)g.getMatrix();
//column 0 //column 1 //column 2
m.m00 = 1; m.m01 = 0; m.m02 = 0; // row 0
m.m10 = 0; m.m11 = 1; m.m12 = 0; // row 1
m.m20 = 0; m.m21 = 0; m.m22 = 1; // row 2
resetMatrix();
applyMatrix(m);
}
...
マスター「g.getMatrix() で現在のマトリクスを取り出した後、」
マスター「m00 ~ m22 のフィールドに値を設定しているだろう?」
マスター「実は、これはマトリクスの要素なんだ」
マスター「そのうち、姿勢変更に関わる要素に単位行列を設定している」

パダワン「あ、掛けても変わんないやつだ!」
マスター「こうすることにより、このまでの過程で」
マスター「ビューイング変換 (camera() のコール) と」
マスター「モデリング変換 (rotateY() や translate() のコール) で変換された」
マスター「『舞台』の位置はそのままに、」
マスター「その姿勢だけを『無かったこと』にできるんだ」
マスター「こうして修正したマトリクス m を」
マスター「現在のマトリクスとして設定し直すのだが、」
マスター「まずは resetMatrix() で」
マスター「現在のマトリクスを単位行列にし、」

マスター「最後に applyMatrix(m) で、」
マスター「現在のマトリクスに m を乗じているんだ」
マスター「改めて実際の動作を確認してみよう」
マスター「新規にスケッチを作成して以下を実行するんだ」
void setup() {
size(1000, 300, P3D);
}
void draw() {
background(255, 255, 255);
stroke(0, 0, 255);
fill(240,240,240);
camera(0, 0, 0, 0, 0, -1, 0, 1, 0); // カメラの視点を原点に置き、視線をZ軸の負の無限大方向に向ける
drawBoard(300, 45); // ローカル座標系を 45°傾けX軸方向に300移動してボードを描画
drawBoard(300, 90); // ローカル座標系を 90°傾けX軸方向に300移動してボードを描画
drawBoard(300, 135); // ローカル座標系を135°傾けX軸方向に300移動してボードを描画
}
void drawBoard(float xpos, float degree) {
pushMatrix();
rotateY(radians(degree)); // Y軸を中心にしてローカル座標系を degree だけ回転
translate(xpos, 0, 0); // ローカル座標系を(ローカル座標系の)x 方向に xpos だけ平行移動
//turnToCamera(); // ローカル座標系のXY平面をカメラ座標系のXY平面と平行にする
beginShape(); // ローカル座標のXY平面に平行なボードを描く
vertex(-50, -50, 0);
vertex( 50, -50, 0);
vertex( 50, 50, 0);
vertex(-50, 50, 0);
endShape(CLOSE);
popMatrix();
}
void turnToCamera() { // ローカル座標系のXY平面をカメラ座標系のXY平面と平行にする
PMatrix3D m = (PMatrix3D)g.getMatrix();
m.m00 = m.m11 = m.m22 = 1;
m.m01 = m.m02 = m.m10 = m.m12 = m.m20 = m.m21 = 0;
resetMatrix();
applyMatrix(m);
}
マスター「実行して確認したら、」
マスター「//turnToCamera(); 部分のコメントを外して」
マスター「改めて実行してみるんだ」
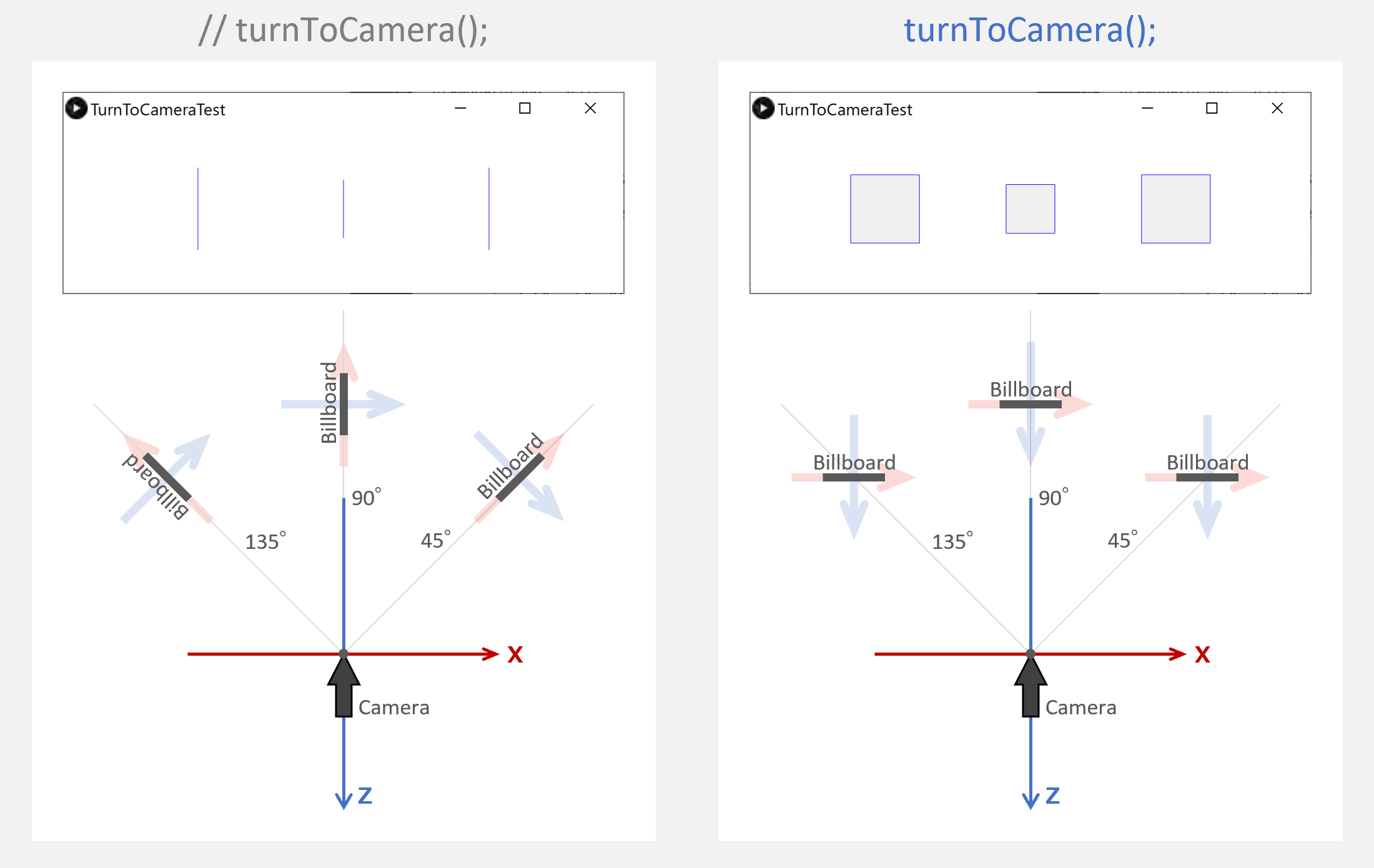
マスター「イメージを掴めたか?」
パダワン「うん!ばっちり!!!」
パダワン(よくわかんないけど、メソッド呼べば振り向いてくれるし!!!)
マスター「なお、1 つだけ補足しておく」
マスター「今回は扱っていないが、」
マスター「scale() や shareX() などの成分も」
マスター「下図の青い部分に含まれるため、」

マスター「例えば、拡大縮小を伴う場合に」
マスター「turnToCamera() は好ましくない挙動をするだろう」
3 時 50 分|ここまでのコード
マスター「ここまでで一区切りついたぞ」
マスター「Learning.pde と Matrix.pde にもう一度目を通しておくんだ」
Learing.pde の全コードを展開
// setup() はプログラム起動直後に一度だけ呼び出される
void setup() {
size(1200, 800, P3D); // ウィンドウサイズと 3DCG の指定
hint(ENABLE_DEPTH_SORT);
//setCameraOrbitalRadius(150);
//setCameraOrbitalPeriod(120);
//setCameraMaxDepth(1500);
setDevRoomAutoCameraEnabled(false);
frameRate(24); // フレームレート (fps)
}
// draw() はプログラムの終了まで何度も呼び出される
// (fps==24 の場合は、1秒間に24回呼び出される)
void draw() {
background(255, 255, 255); // 背景色(R,G,B) は白
//updateCamera1();
//updateCamera2();
updateCamera3();
updateDevRoom();
updateObject1();
updateObject2();
updateObject3();
updateObject4();
//updateObject5();
//updateObject6();
//updateObject7();
//updateObject8();
//updateObject9();
//updateObject10()
//updateObject11();
//updateObject12();
//updateObject13();
}
// (1) 矩形の描画(静止)
void updateObject1() {
fill(240, 240, 240); // 塗りつぶし色(R,G,B)
stroke(255, 0, 255); // 枠線の色(R,G,B)
strokeWeight(2); // 枠線の太さ
beginShape();
vertex(-50, -50, -500);
vertex( 50, -50, -500);
vertex( 50, 50, -500);
vertex(-50, 50, -500);
endShape(CLOSE);
}
// (2) 矩形の描画(疑似等速直線運動)
float gZ = -600;
void updateObject2() {
gZ+=120; // Z座標の更新
fill(255, 255, 255); // 塗りつぶし色(R,G,B)
stroke(0, 255, 255); // 枠線の色(R,G,B)
strokeWeight(2); // 枠線の太さ
beginShape();
vertex(-40, -40, gZ);
vertex( 40, -40, gZ);
vertex( 40, 40, gZ);
vertex(-40, 40, gZ);
endShape(CLOSE);
}
// (3) 矩形の描画(リアル等速直線運動)
void updateObject3() {
final float START_Y = -600; // 開始時点のY座標
final float SPEED = 200; // 秒速
float ms = millis(); // プログラム開始時点からの経過ミリ秒
float dy = ms * SPEED / 1000; // 移動距離(Y座標)
float y = START_Y + dy; // 現在位置(Y座標)
noFill(); // 塗りつぶしなし
stroke(255, 0, 0); // 枠線の色(R,G,B)
strokeWeight(2); // 枠線の太さ
beginShape();
vertex(-30, y, -30);
vertex( 30, y, -30);
vertex( 30, y, 30);
vertex(-30, y, 30);
endShape(CLOSE);
}
// (4) 矩形の描画(円運動)
void updateObject4() {
final float R = 500; // 公転半径
final float SPEED = 60; // 角度(Degree)/秒
float ms = millis(); // プログラム開始時点からの経過ミリ秒
float dd = ms * SPEED / 1000; // 移動角度(Degree)
float dr = radians(dd); // 移動角度(Radian)
float x = R * cos(dr); // X座標
float y = R * sin(dr); // Y座標
fill(255, 255, 255); // 塗りつぶし色(R,G,B)
stroke(0, 0, 255); // 枠線の色(R,G,B)
strokeWeight(2); // 枠線の太さ
beginShape();
vertex(x-30, y, -30);
vertex(x+30, y, -30);
vertex(x+30, y, 30);
vertex(x-30, y, 30);
endShape(CLOSE);
}
// (5) 3次元オブジェクトの描画(静止)
void updateObject5() {
noFill(); // 塗りつぶしなし
strokeWeight(2); // 枠線の太さ
stroke(255, 0, 255); // 枠線の色(R,G,B)
box(150);
stroke(0, 255, 255); // 枠線の色(R,G,B)
sphere(60);
}
// (6) 3次元オブジェクト(座標変換で等速直線運動)
// (3) と似た動きを座標変換で実現
void drawEarth() {
fill(224, 224, 255); // 塗りつぶし色(R,G,B)
stroke(0, 0, 255); // 枠線の色(R,G,B)
strokeWeight(2); // 枠線の太さ
box(80);
}
void updateObject6() {
final float START = -600; // 開始時点の位置
final float SPEED = 200; // 秒速
float ms = millis(); // プログラム開始時点からの経過ミリ秒
float d = ms * SPEED / 1000; // 移動距離
float p = START + d; // 現在位置
pushMatrix();
translate(p, -100, 50);
drawEarth();
popMatrix();
}
// (7) 3次元オブジェクト(座標変換で自転)
void updateObject7() {
final float SPEED = 60; // 角度(Degree)/秒
float ms = millis(); // プログラム開始時点からの経過ミリ秒
float dd = ms * SPEED / 1000; // 移動角度(Degree)
float dr = radians(dd); // 移動角度(Radian)
pushMatrix();
rotateY(dr);
drawEarth();
popMatrix();
}
// (8) 3次元オブジェクト(座標変換で公転)
// (4) と似た動きを座標変換で実現
void updateObject8() {
final float R = 300; // 公転半径
final float SPEED = 150; // 角度(Degree)/秒
float ms = millis(); // プログラム開始時点からの経過ミリ秒
float dd = ms * SPEED / 1000; // 移動角度(Degree)
float dr = radians(dd); // 移動角度(Radian)
pushMatrix();
rotateY(dr);
translate(R, 0, 0);
drawEarth();
popMatrix();
}
// (9) 3次元オブジェクト(座標変換で離れた位置で自転)
// (8) との違いに注目
void updateObject9() {
final float R = 300; // 公転半径
final float SPEED = 150; // 角度(Degree)/秒
float ms = millis(); // プログラム開始時点からの経過ミリ秒
float dd = ms * SPEED / 1000; // 移動角度(Degree)
float dr = radians(dd); // 移動角度(Radian)
pushMatrix();
translate(R, 0, 0); // 順序を入れ替えただけ
rotateY(dr); // 順序を入れ替えただけ
drawEarth();
popMatrix();
}
// (10) 3次元オブジェクト(座標変換で公転体の周りを公転)
void drawSun() {
noFill(); // 塗りつぶしなし
stroke(255, 0, 0); // 枠線の色(R,G,B)
strokeWeight(2); // 枠線の太さ
sphere(60);
}
void drawMoon() {
fill(255, 255, 128); // 塗りつぶし色(R,G,B)
stroke(255, 0, 0); // 枠線の色(R,G,B)
strokeWeight(2); // 枠線の太さ
beginShape();
vertex(-20, -20, 0);
vertex( 20, -20, 0);
vertex( 20, 20, 0);
vertex(-20, 20, 0);
endShape(CLOSE);
}
void updateObject10() {
float ms = millis(); // プログラム開始時点からの経過ミリ秒
final float E_R = 400; // 地球の公転半径
final float E_SPEED = 80; // 地球の角度(Degree)/秒
float edd = ms * E_SPEED / 1000; // 地球の移動角度(Degree)
float edr = radians(edd); // 地球の移動角度(Radian)
final float M_R = 100; // 月の公転半径
final float M_SPEED = 200; // 月の角度(Degree)/秒
float mdd = ms * M_SPEED / 1000; // 月の移動角度(Degree)
float mdr = radians(mdd); // 月の移動角度(Radian)
drawSun();
pushMatrix();
{
rotateY(edr);
translate(E_R, 0, 0);
drawEarth();
pushMatrix();
{
rotateY(mdr);
translate(M_R, 0, 0);
drawMoon();
}
popMatrix();
}
popMatrix();
}
// (11) テクスチャマッピング(静止)
void drawGopher(float len) {
PImage img = loadImage("gopher.png");
int h = img.height;
int w = img.width;
noStroke(); // 枠線を描画しない
beginShape();
texture(img);
vertex(-len/2, -len/2, 0, 0, 0);
vertex( len/2, -len/2, 0, w, 0);
vertex( len/2, len/2, 0, w, h);
vertex(-len/2, len/2, 0, 0, h);
endShape();
}
void updateObject11() {
drawGopher(500);
}
// (12) テクスチャマッピング(座標変換で公転体の周りを公転)
// 動きは (10) とほぼ同じ
void updateObject12() {
float ms = millis(); // プログラム開始時点からの経過ミリ秒
final float S_LEN = 200; // 太陽Gopherの1辺の長さ
final float E_LEN = 100; // 地球Gopherの1辺の長さ
final float E_R = 400; // 地球Gopherの公転半径
final float E_SPEED = 80; // 地球Gopherの角度(Degree)/秒
float edd = ms * E_SPEED / 1000; // 地球Gopherの移動角度(Degree)
float edr = radians(edd); // 地球Gopherの移動角度(Radian)
final float M_LEN = 50; // 月Gopherの1辺の長さ
final float M_R = 100; // 月Gopherの公転半径
final float M_SPEED = 200; // 月Gopherの角度(Degree)/秒
float mdd = ms * M_SPEED / 1000; // 月Gopherの移動角度(Degree)
float mdr = radians(mdd); // 月Gopherの移動角度(Radian)
pushMatrix();
{
translate(0, -S_LEN / 2, 0);
drawGopher(S_LEN); // 太陽Gopher
}
popMatrix();
pushMatrix();
{
rotateY(edr);
translate(E_R, 0, 0);
pushMatrix();
{
translate(0, -E_LEN / 2, 0);
drawGopher(E_LEN); // 地球Gopher
}
popMatrix();
pushMatrix();
{
rotateY(mdr);
translate(M_R, -M_LEN / 2, 0);
drawGopher(M_LEN); // 月Gopher
}
popMatrix();
}
popMatrix();
}
// (13) ビルボード(座標変換で公転体の周りを公転)
// 動きは (12) とほぼ同じ
void turnToCamera() {
PMatrix3D m = (PMatrix3D)g.getMatrix();
//column 0 //column 1 //column 2
m.m00 = 1; m.m01 = 0; m.m02 = 0; // row 0
m.m10 = 0; m.m11 = 1; m.m12 = 0; // row 1
m.m20 = 0; m.m21 = 0; m.m22 = 1; // row 2
resetMatrix();
applyMatrix(m);
}
void updateObject13() {
float ms = millis(); // プログラム開始時点からの経過ミリ秒
final float S_LEN = 200; // 太陽Gopherの1辺の長さ
final float E_LEN = 100; // 地球Gopherの1辺の長さ
final float E_R = 400; // 地球Gopherの公転半径
final float E_SPEED = 80; // 地球Gopherの角度(Degree)/秒
float edd = ms * E_SPEED / 1000; // 地球Gopherの移動角度(Degree)
float edr = radians(edd); // 地球Gopherの移動角度(Radian)
final float M_LEN = 50; // 月Gopherの1辺の長さ
final float M_R = 100; // 月Gopherの公転半径
final float M_SPEED = 200; // 月Gopherの角度(Degree)/秒
float mdd = ms * M_SPEED / 1000; // 月Gopherの移動角度(Degree)
float mdr = radians(mdd); // 月Gopherの移動角度(Radian)
pushMatrix();
{
translate(0, -S_LEN / 2, 0);
turnToCamera();
drawGopher(S_LEN); // 太陽Gopher
}
popMatrix();
pushMatrix();
{
rotateY(edr);
translate(E_R, 0, 0);
pushMatrix();
{
translate(0, -E_LEN / 2, 0);
turnToCamera();
drawGopher(E_LEN); // 地球Gopher
}
popMatrix();
pushMatrix();
{
rotateY(mdr);
translate(M_R, -M_LEN / 2, 0);
turnToCamera();
drawGopher(M_LEN); // 月Gopher
}
popMatrix();
}
popMatrix();
}
// (14) カメラ制御(静止)
void updateCamera1() {
float x = 25;
float y = -70;
float z = 800;
camera(x, y, z, 0, 0, 0, 0, 1, 0);
}
// (15)カメラ制御(等速直線運動)
void updateCamera2() {
final float START_Z = 1500; // 開始時点のZ座標
final float SPEED = -300; // 秒速-300
float ms = millis(); // プログラム開始時点からの経過ミリ秒
float dz = ms * SPEED / 1000; // 移動距離(Y座標)
float x = 100;
float y = -50;
float z = START_Z + dz; // 現在位置(Y座標)
//camera(x, y, z, x, y, z-1, 0, 1, 0);
camera(x, y, z, 0, 0, 0, 0, 1, 0);
}
// (16) カメラ制御(公転)
void updateCamera3() {
final float R = 1500; // 公転半径
final float SPEED = 15; // 角度(Degree)/秒
float ms = millis(); // プログラム開始時点からの経過ミリ秒
float dd = ms * SPEED / 1000; // 移動角度(Degree)
float dr = radians(dd); // 移動角度(Radian)
float x = R * cos(dr); // X座標
float z = R * sin(dr); // Z座標
float y = -50;
camera(x, y, z, 0, 0, 0, 0, 1, 0);
}
Matrix.pde の全コードを展開
size(500,500,P3D);
// マトリクスの確認
println("----------------------------------");
resetMatrix(); println("resetMatrix();");
printMatrix();
pushMatrix();
translate(-3, 0, -3); println("translate(-3, 0, -3);");
printMatrix();
popMatrix();
rotateY(radians(30)); println("rotateY(radians(30));");
printMatrix();
// 合成変換の確認
println("----------------------------------");
resetMatrix();
rotateY(radians(30)); println("rotateY(radians(30));");
printMatrix();
resetMatrix();
rotateX(radians(30)); println("rotateX(radians(30));");
printMatrix();
resetMatrix();
rotateY(radians(30)); println("rotateY(radians(30));");
rotateX(radians(30)); println("rotateX(radians(30));");
printMatrix();
// マトリクス同士の乗算
println("----------------------------------");
float[] m1 = new float[16]; // rotateY() の結果
float[] m2 = new float[16]; // rotateX() の結果
float[] m3 = new float[16]; // rotateY() と rotateX() の合成結果
resetMatrix();
rotateY(radians(30));
((PMatrix3D)g.getMatrix()).get(m1);
resetMatrix();
rotateX(radians(30));
((PMatrix3D)g.getMatrix()).get(m2);
for (int i = 0; i < 4; i++)
for (int j = 0; j < 4; j++)
for (int k = 0; k < 4; k++)
m3[i * 4 + j] += m1[i * 4 + k] * m2[k * 4 + j];
println(m3);
// カメラの挙動
println("----------------------------------");
camera(50, 0, 100, 50, 0, 0, 0, 1, 0);
println("camera(50, 0, 100, 50, 0, 0, 0, 1, 0);");
printMatrix();
camera(0, 0, 0, 250, 0, -433, 0, 1, 0);
println("camera(0, 0, 0, 250, 0, -433, 0, 1, 0);");
printMatrix();
// 座標変換との比較
println("----------------------------------");
resetMatrix();
translate(-50, 0, -100);
println("translate(-50, 0, -100);");
printMatrix();
resetMatrix();
rotateY(radians(30));
println("rotateY(radians(30));");
printMatrix();
午前 4 時|クラス設計と実装
4 時 00 分|実装の準備
マスター「ここからいよいよシミュレーターの製作だ」
パダワン「お!やっと …(笑)」
マスター「だが、その前に、Processing 公式サイトの」
マスター「リファレンスページの URL を教えておこう」
マスター「まだ教えていないメソッドなどがいろいろあるから、」
マスター「調べながら実装を進めるんだ」
マスター「そうしたら開発を進めていくが、」
マスター「まずは [ファイル][新規] で新規スケッチを開いて、」
マスター「Simurator という名前で保存するんだ」
マスター「次に [▼][新規タブ] で DevUtils という名前のタブを作成して」
マスター「ユーティリティのコードを貼り付けるんだ」
マスター「さっきやったから細かい説明は要らないな?」
パダワン「うん。楽勝!」
すると、そこへ Gopher君の集団が姿を現した。
パダワン「あれれ? 消えたと思ったら、いつの間に …」
パダワン「しかも派手な格好で登場(笑)」
| 太陽 Gopher君 | 水星 Gopher君 | 金星 Gopher君 |
|---|---|---|
gp_sun.png
|
gp_mercury.png
|
gp_venus.png
|
| 地球 Gopher君 | 月 Gopher君 | 火星 Gopher君 |
|---|---|---|
gp_earth.png
|
gp_moon.png
|
gp_mars.png
|
| 木星 Gopher君 | 土星 Gopher君 | 天王星 Gopher君 |
|---|---|---|
gp_jupiter.png
|
gp_saturn.png
|
gp_uranus.png
|
| 海王星 Gopher君 | 青星 Gopher君 | 白星 Gopher君 |
|---|---|---|
gp_neptune.png
|
gp_50_blue.png |
gp_50_white.png |
| 黄星 Gopher君 | 橙星 Gopher君 | 赤星 Gopher君 |
|---|---|---|
gp_50_yellow.png |
gp_50_orange.png |
gp_50_red.png |
マスター「太陽系の詳しい資料が揃うまで」
マスター「Gopher君が各天体の代役をやってくれることになったんだ」
パダワン「うげっ! 天王星Gopher君かっけー!!!」
パダワン「青星君とか赤星君はなにもん???」
マスター「恒星の表面温度ごとに、5 種類を準備してもらったんだ」
マスター「ホロカムを PNG にしたから、」
マスター「スケッチフォルダーに data フォルダーを作成して」
マスター「これをそこへコピーするんだ」
マスター「なお、メモリ節約のために」
マスター「青星~赤星君の 5 つのファイルは」
マスター「サイズが 50 x 50 の小さい方をコピーするんだ」
マスター「次のようなディレクトリ構成になったはずだ」
any-dir
Simulator
├── Simulator.pde
├── DevUtils.pde
└── data
├── gp_50_blue.png
├── gp_50_orange.png
├── gp_50_red.png
├── gp_50_white.png
├── gp_50_yellow.png
├── gp_earth.png
├── gp_jupiter.png
├── gp_mars.png
├── gp_mercury.png
├── gp_moon.png
├── gp_neptune.png
├── gp_saturn.png
├── gp_sun.png
├── gp_uranus.png
└── gp_venus.png
マスター「そうしたら、シミュレーターの」
マスター「ざっくりとした設計方針を検討しよう」
マスター「描画するオブジェクトは、」
マスター「中心に位置する太陽、」
マスター「それから惑星とその衛星、」
マスター「そして銀河の星々だ」
パダワン「銀河???」
マスター「そうだ。今回の要求では、銀河の星々は」
マスター「ワールド座標系で静止していると考えて良い」
パダワン「あっ、だから青色Gopher君たちが居るのか!」
マスター「また、太陽はワールド座標系の」
マスター「原点 (0, 0, 0) に静止させた方が作りやすいだろう」
マスター「あとは、母星を中心に公転する惑星と衛星だな」
4 時 10 分|Billboard クラス
マスター「まずは基本となるビルボードのクラスだが、」
マスター「これまでビルボードを表示するときに」
マスター「どんな属性を指定した?」
パダワン「看板の大きさと、貼り付ける画像と …」
パダワン「あっ!表示する場所だ!」
マスター「そうだな。」
マスター「そうするとクラス定義は以下のようになるだろうな」
Billboard クラス
| カテゴリ | 項目 | 説明 |
|---|---|---|
| class | Billboard | カメラ方向への姿勢変更など、ビルボードの基本機能を実装する。 |
| field | mImage | ビルボードに貼り付ける画像。 |
| field | mWidth | ビルボードの幅。 |
| field | mHeight | ビルボードの高さ。 |
| field | mX | ビルボードのX座標。 |
| field | mY | ビルボードのY座標。 |
| field | mZ | ビルボードのZ座標。 |
| method | update() | 座標変換して描画する。継承先がオーバーライドしやすいよう、transform() と drawSelf() を分けておく。 |
| method | transform() | 座標変換する。 |
| method | drawSelf() | 自身を描画する。 |
マスター「よし、そうしたらこれで実装してみよう」
マスター「[▼][新規タブ] で Billboard という名前のタブを作成して」
マスター「そこに書いてみろ」
パダワン「えーと、Learning.pde からコピペしながら …」
パダワンは次のようなセーバーを書いた。
// ビルボードクラス
public class Billboard {
private PImage mImage; // ビルボードに貼り付ける画像
private int mWidth; // ビルボードの幅
private int mHeight; // ビルボードの高さ
private float mX; // ビルボードのX座標
private float mY; // ビルボードのY座標
private float mZ; // ビルボードのZ座標
// コンストラクタ
// param imageName: 貼り付ける画像のファイル名
// param w : ビルボードの幅
// param x : ビルボードのX座標
// param y : ビルボードのY座標
// param z : ビルボードのZ座標
public Billboard(String imageName, int w, float x, float y, float z) {
this( loadImage(imageName), w, x, y, z);
}
// コンストラクタ
// param image: 貼り付ける画像
// param w : ビルボードの幅
// param x : ビルボードのX座標
// param y : ビルボードのY座標
// param z : ビルボードのZ座標
public Billboard(PImage image, int w, float x, float y, float z) {
mImage = image;
mWidth = w;
mHeight = w * mImage.height / mImage.width; // 高さは画像の縦横比から計算
mX = x;
mY = y;
mZ = z;
}
// 座標変換して描画
public void update() {
pushMatrix();
transform();
turnToCamera();
drawSelf();
popMatrix();
}
// 座標変換
protected void transform() {
translate(mX, mY, mZ);
}
// 描画
protected void drawSelf() {
float hw = mWidth / 2;
float hh = mHeight / 2;
float iw = mImage.width;
float ih = mImage.height;
pushStyle();
noStroke();
beginShape();
texture(mImage);
vertex(-hw, -hh, 0, 0, 0);
vertex( hw, -hh, 0, iw, 0);
vertex( hw, hh, 0, iw, ih);
vertex(-hw, hh, 0, 0, ih);
endShape();
popStyle();
}
// カメラ方向に姿勢変更
protected void turnToCamera() {
PMatrix3D m = (PMatrix3D)g.getMatrix();
m.m00 = m.m11 = m.m22 = 1;
m.m01 = m.m02 = m.m10 = m.m12 = m.m20 = m.m21 = 0;
resetMatrix();
applyMatrix(m);
}
}
パダワン「コンストラクタは 2 つ用意したよ!」
パダワン「ファイル名を指定するやつと、」
パダワン「画像オブジェクトを指定するやつ」
マスター「そうだな。必要になってからでも良いが、」
マスター「その 2 つは先に用意しておいてもいいだろう」
パダワン「あと、 update() は誰でも呼び出せるように」
パダワン「public にして、」
パダワン「それ以外はサブクラスから使えるように」
パダワン「protected にしといた」
マスター「まあ、そうだな」
マスター「実は Processing で作成したクラスは、」
マスター「Processing の内部で生成されるクラスの」
マスター「インナークラスとしてビルドされるから、」
マスター「プライベートメンバーなども」
マスター「見えるところからは見えてしまうんだが、」
マスター「まあ、それで良いだろう」
マスター「ん? pushStyle() と popStyle() を使ったのか?」
パダワン「うん。さっきリファレンスページで見た」
パダワン「マトリクスのときみたいに、」
パダワン「プッシュしたら色とか線の太さとかを」
パダワン「取っとけるのかなと思って試しに書いてみた(笑)」
マスター「そうだ。それでいい!」
マスター(やはりこの子は直観で動くタイプだな)
マスター「そうしたら、」
マスター「Billboard クラスを使って描画してみよう」
マスター「Simurator タブにそれを書くんだ」
パダワン「えーと、、」
パダワン「そしたら、青星君と赤星君使うー!」
Billboard gStarBlue;
Billboard gStarRed;
void setup() {
gStarBlue = new Billboard("gp_50_blue.png", 50, 400, -25, 400);
gStarRed = new Billboard("gp_50_red.png" , 30, 400, -15, 200);
size(1920, 1080, P3D);
hint(ENABLE_DEPTH_SORT);
frameRate(24);
}
void draw() {
background(255, 255, 255);
updateDevRoom();
gStarBlue.update();
gStarRed.update();
}
セーバーを書き終えると、パダワンは [実行] ボタンをクリックした。
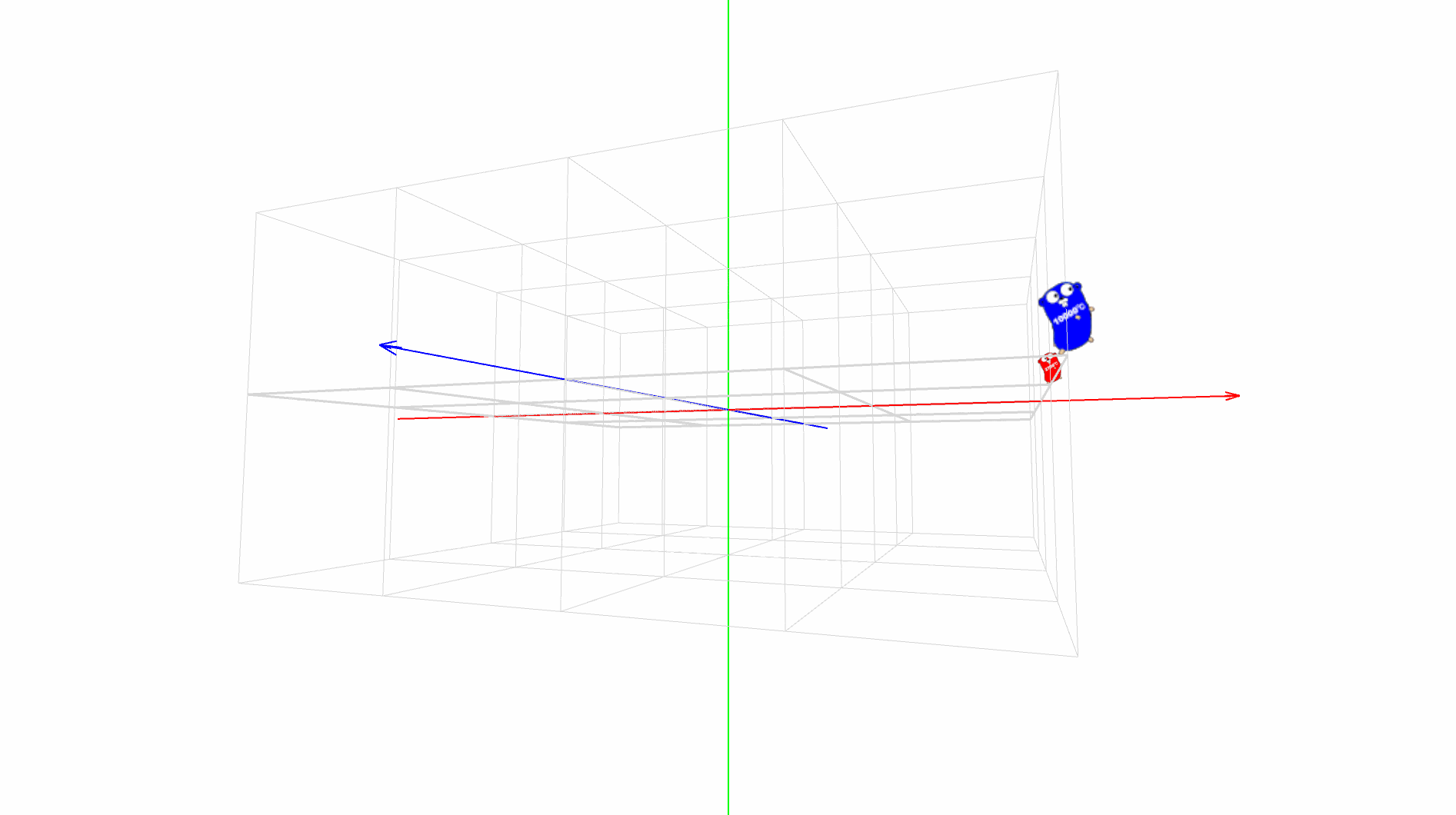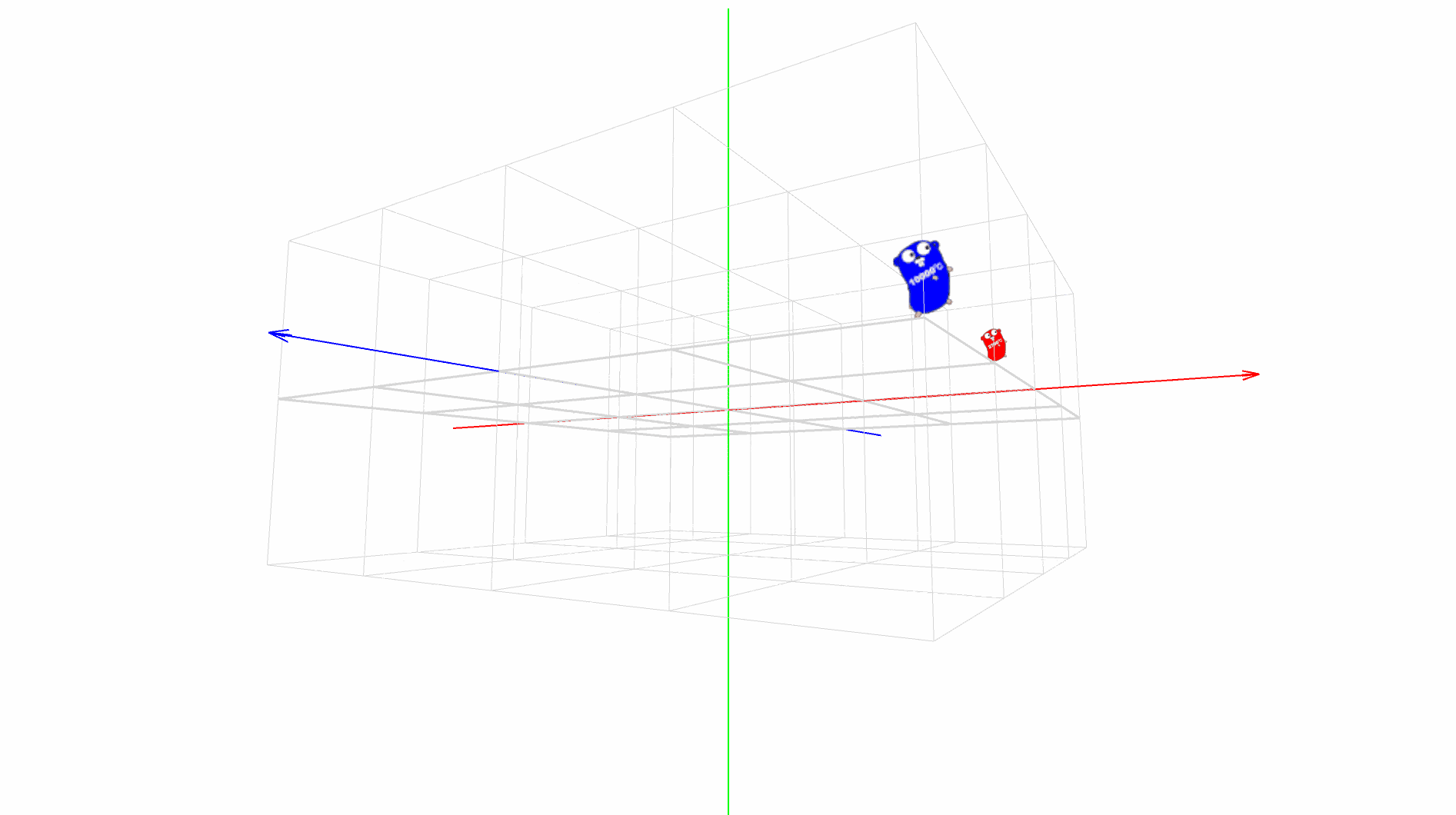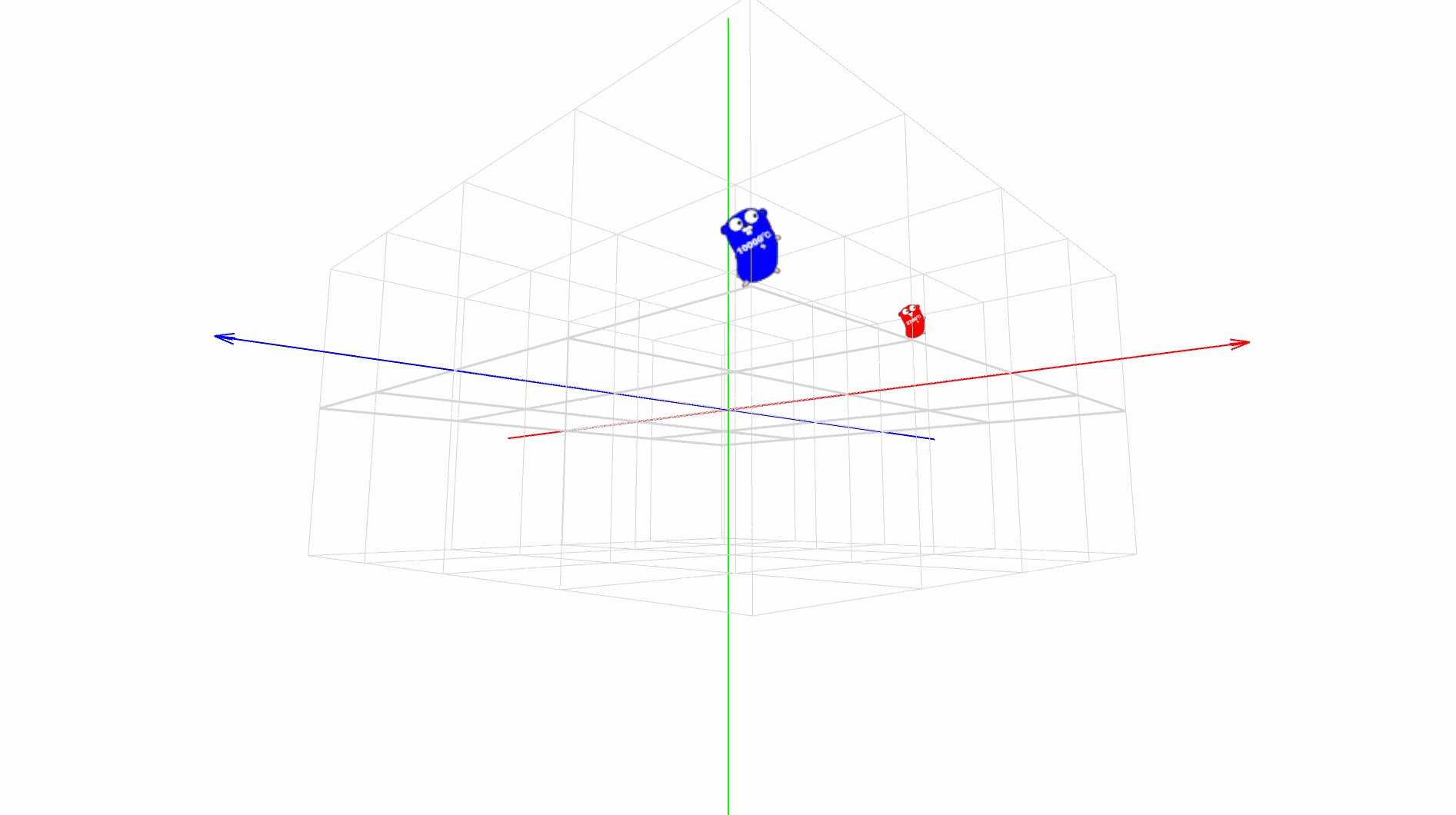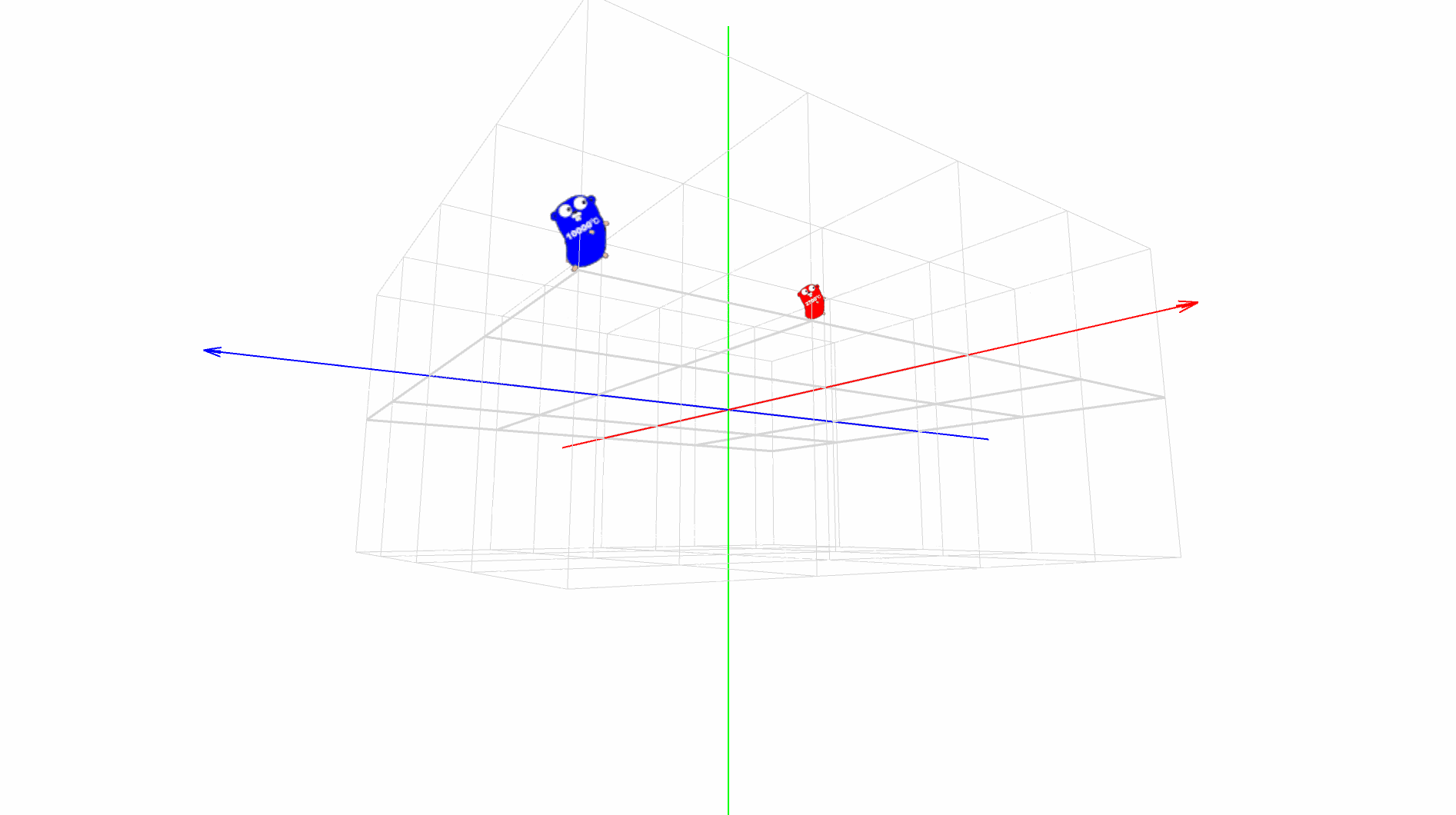
マスター「どうだ?」
パダワン「うん。指定した位置にバッチリ表示されてる」
パダワン「楽勝すぎて泣けてくる!!!(笑)」
4 時 20 分|Galaxy クラス
マスター「よし。そうしたら、Billboard クラスを使って」
マスター「銀河の星々を描くぞ」
マスター「少なくとも 1000 個程度は描画する必要があるから …」
パダワン「ひぇっ! 1000 個も?!」
マスター「ああ、そうだ」
マスター「だから位置指定に乱数を使おう」
マスター「random() というメソッドが」
マスター「乱数を返してくれるから少し説明しよう」
- このメソッドは、例えば、
random(100)とすれば、0 <= result < 100 の範囲で浮動小数点数を返してくれて、 -
random(3, 10)とすれば、3 <= result < 10 の範囲で浮動小数点数をかえしてくれるんだ。
マスター「これらを考慮すると、」
マスター「Galaxy クラスは次のようになるだろう」
Galaxy クラス
| カテゴリ | 項目 | 説明 |
|---|---|---|
| class | Galaxy | 銀河系クラス。1000個程度の銀河の星々を表示する。各星は Billboard クラスで実装する。ビルボードに貼り付ける画像や座標は乱数で決定する。 |
| field | mStars | Billboard の配列。 |
| method | update | すべての星を描画する。 |
なお、星々を描画する仕様は次の通りとする。
-
ZX 方向
原点 (0, 0, 0) からの距離を 4000 ~ 5000 の範囲とする。つまり原点を中心とする半径4000の円と半径5000の円の間に収まるようにする。 -
Y 方向
-3000 ~ 3000 の範囲とする。 - 恒星の表面温度が高い順から、青、白、黄、オレンジ、赤の5種類をランダムに表示する。
マスター「そうしたら新規タブで Galaxy を作成し、」
マスター「そこに実装するんだ」
パダワン「えーと、、2π は 180° …」
パダワン「あは! 覚えたかも(笑)」
// 銀河を構成する星々
public class Galaxy {
private Billboard[] mStars = new Billboard[1000]; // 星の数だけのビルボード
// コンストラクタ
public Galaxy() {
// 画像配列の初期化
PImage[] images = new PImage[] {
loadImage("gp_50_blue.png"),
loadImage("gp_50_white.png"),
loadImage("gp_50_yellow.png"),
loadImage("gp_50_orange.png"),
loadImage("gp_50_red.png"),
};
// 星の数だけループ
for (int i = 0; i < mStars.length; i++) {
float angle = random(TWO_PI); // ZX平面上の角度は0~360°(2π)の範囲でランダムに
float radius = random(4000, 5000); // ZX平面上の原点からの距離は4000~5000の範囲でランダムに
float x = sin(angle) * radius; // 星のX座標
float z = cos(angle) * radius; // 星のZ座標
float y = random(-3000, 3000); // 星のY座標は-3000~3000の範囲でランダムに
int n = (int)random(5); // ビルボードに貼り付ける画像は5種類からランダムに
mStars[i] = new Billboard(images[n], 50, x, y, z); // ビルボードを生成して配列に格納
}
}
// すべての星を座標変換して描画する
public void update() {
for (Billboard star: mStars) {
star.update();
}
}
}
パダワン「えーと、、」
パダワン「5 つの画像を配列に入れてランダムに選ぶ場合は」
パダワン「int 型にダウンキャストしちゃったけど、、」
パダワン(正の数なら、切り捨て怖くねー!)
(脚注:Episode I を参照のこと)
パダワン「でも、これでいいのかなぁ?」
マスター「それなら実際に動かして確かめてみるんだ」
パダワン「えーと、Simulator タブを開いてっと、、」
パダワン「これはオブジェクト作って呼び出すだけだから」
パダワン「楽勝!楽勝!(笑)」
//Billboard gStarBlue; // ---
//Billboard gStarRed; // ---
Galaxy gGalaxy; // +++
void setup() {
//gStarBlue = new Billboard("gp_50_blue.png" , 50, 400, -25, 400); // ---
//gStarRed = new Billboard("gp_50_red.png" , 30, 400, -15, 200); // ---
gGalaxy = new Galaxy(); // +++
size(1920, 1080, P3D);
hint(ENABLE_DEPTH_SORT);
frameRate(24);
}
void draw() {
background(255, 255, 255);
updateDevRoom();
//gStarBlue.update(); // ---
//gStarRed.update(); // ---
gGalaxy.update(); // +++
}
パダワン「// --- は削除したとこで、」
パダワン「// +++ は追記したとこね!」
パダワン「あ、でも、ぜんぶの色が表示されてるよ」
パダワン「ダウンキャストで良かったみたい!」
4 時 30 分|CelestialObject クラス
マスター「そうしたら、次に作るのは」
マスター「かるがもビルボードだな」
パダワン「え?かるがも???」
マスター「そうだ。かるがもの親子のように」
マスター「子を引き連れることができるビルボードだ」
パダワン(いいなぁ、かるがも …)
パダワン(僕にはパパもママも居ないから羨ましいや)
マスター「さっき、Learning.pde を作ったときに」
マスター「地球のローカル座標を月に反映させたのを覚えてるか?」
パダワン「あ、月が自分の場所だけ考えて回ってるのに」
パダワン「勝手に地球についてくやつでしょ?」
マスター「そうだ。惑星を引き連れる太陽や、」
マスター「衛星を引き連れる惑星に共通する振舞いを」
マスター「ビルボードに実装するんだ」
パダワン「ビルボードに追記するの?」
パダワン「でも、銀河の星さんたちは子供連れてないよ!」
マスター「そうだな」
マスター「まあ、Billboard クラスに直接実装してもいいし、」
マスター「Billboard を継承するクラスを新たに作ってもいいぞ」
パダワン「じゃー、新しく作る!」
マスター「そうしたら、CelestialObject とでも名付けて」
マスター「次のような機能を実装しよう」
CelestialObject クラス
| カテゴリ | 項目 | 説明 |
|---|---|---|
| class | CelestialObject | 公転体の親クラス。自身のローカル座標系の影響を受ける、複数の子(ビルボード)を持つことができる。 |
| extends | Billboard | |
| field | mChildren | 子のリスト。 |
| method | addChild() | 子を追加する。 |
| method | update() | オーバーライド。自身の座標変換と描画を終えたら、すべての子の update() を呼び出す。 |
マスター「新規タブで CelestialObject を作成し、」
マスター「そこに実装してみろ」
パダワン「えーと、リファレンス、リファレンス …」
パダワン「おっ!ArrayList が使えるぞ!」
パダワン「るるる~♪」
パダワン「リストとクスリはジェネリック~♪」
パダワン「スピーカーはジェネレック~♪」
パダワン「っと …」
// 天体クラス(子がいれば一緒に描画)
public class CelestialObject extends Billboard {
private ArrayList<Billboard> mChildren = null; // 子供リスト
// コンストラクタ
// param imageName 画像ファイル名
// param w 天体(ビルボード)の幅
// param x 天体(ビルボード)のX座標
// param y 天体(ビルボード)のY座標
// param z 天体(ビルボード)のZ座標
public CelestialObject(String imageName, int w, float x, float y, float z) {
super(imageName, w, x, y, z);
}
// 子供を追加する
public void addChild(Billboard child) {
if (mChildren == null) {
mChildren = new ArrayList<Billboard>();
}
mChildren.add(child);
}
public void update() {
pushMatrix();
transform();
turnToCamera();
drawSelf(); // 自分を描画
updateChildren(); // すべての子供を描画
popMatrix();
}
private void updateChildren() {
if (mChildren != null) {
for (Billboard child : mChildren) {
child.update();
}
}
}
}
パダワン「えーと、」
パダワン「ArrayList はコンストラクタで作らないで、」
パダワン「addChild() で最初の子供を追加するときだけ」
パダワン「作るようにしたよ」
パダワン「で、update() はオーバーライドして、」
パダワン「popMatrix() を呼ぶ前に子どもたちを」
パダワン「アップデートするようにした」
パダワン「あと、子供たちは updateChildren() に切り分けたけど、」
パダワン「これは他から使わないだろうから private にした!」
パダワン「あ、でも updateChildren() を呼ぶ前に、」
パダワン「turnToCamera() と drawSelf() を」
パダワン「pushMatrix() と popMatrix() で」
パダワン「括った方が良かったのかなぁ?」
マスター「そうしたら、」
マスター「実際に動かしてみて確かめてみよう」
マスター「Simulator.pde に追記して」
マスター「太陽とその子を作ってテストしてみるんだ」
マスター「太陽だけ update() すれば」
マスター「他の惑星も描画されるってところが重要だ」
パダワン「うん。それなら …」
パダワン「太陽の前後左右を最強の布陣で固めよう(笑)」
Galaxy gGalaxy;
CelestialObject gSun; // +++
void setup() {
gGalaxy = new Galaxy();
gSun = new CelestialObject("gp_sun.png", 300, 0, 0, 0); // +++
CelestialObject earth = new CelestialObject("gp_earth.png", 100, -200, 0, 0); // +++
CelestialObject jupiter = new CelestialObject("gp_jupiter.png", 100, 200, 0, 0); // +++
CelestialObject saturn = new CelestialObject("gp_saturn.png", 100, 0, 0, -200); // +++
CelestialObject uranus = new CelestialObject("gp_uranus.png", 100, 0, 0, 200); // +++
gSun.addChild(earth); // +++
gSun.addChild(jupiter); // +++
gSun.addChild(saturn); // +++
gSun.addChild(uranus); // +++
size(1920, 1080, P3D);
hint(ENABLE_DEPTH_SORT);
frameRate(2);
}
void draw() {
background(255, 255, 255);
updateDevRoom();
gGalaxy.update();
gSun.update(); // +++
}
パダワン「あれれ???」
パダワン「なんか変 …」
パダワン「止まってる?」

パダワン「あ!止まってるってことは、、」
パダワン「カメラと一緒に動いてるんだ!!!」
パダワン「太陽君の前にいる天王星君の雄姿がずっと見える(笑)」
パダワン「そっか、、」
パダワン「turnToCamera() か …」
パダワンは CelestialObject.pde を次のように書き換えてみた。
...
public void update() {
pushMatrix();
transform();
pushMatrix(); // +++
turnToCamera();
drawSelf(); // 自分を描画
popMatrix(); // +++
updateChildren(); // すべての子供を描画
popMatrix();
}
...

マスター「そうだな。turnToCamera() は、」
マスター「ローカル座標系とワールド座標系の回転成分をリセットして」
マスター「カメラ座標系に合わせてしまうから、」
マスター「ワールド座標系を中心に考えると」
マスター「そこに静止しているはずのオブジェクトが」
マスター「カメラと一緒に動いてしまうんだ」
4 時 40 分|OrbitalObject クラス
マスター「よし。そうしたら、」
マスター「あとは惑星や衛星の振舞いをするクラスの作成だな」
マスター「公転体に必要なのはどんな属性だ?」
パダワン「えーと、半径と、、」
パダワン「あっ!回る速さだ!!!」
マスター「そうだな。仕様は次のような感じになるだろう」
OrbitalObject クラス
| カテゴリ | 項目 | 説明 |
|---|---|---|
| class | OrbitalObject | 公転体クラス。親となる天体を中心に円運動をする。天体の軌道を描画する。 |
| extends | CelestialObject | |
| field | mRadius | 公転半径 |
| field | mPeriod | 公転周期 |
| mehtod | transform() | オーバーライド。公転半径と公転周期に従って座標変換する。 |
パダワン「うん!これができれば大体できあがりだね!」
マスター「そうなんだが、、」
マスター「まだシミュレートに必要なデータが揃っていないんだ」
マスター「だから、これから私はテンプルにある共和騎士図書館で」
マスター「太陽系の情報を収集してくる」
マスター「その間、お前は Gopher君と実装を進めなさい」
マスター「そして、できれば天体の軌道を表示するところまでを」
マスター「1 人でやってみろ」
パダワン「うん!楽勝(笑)」
マスター「じゃあ私は図書館に行ってくるぞ!」
マスター「収集した情報は随時送信する」
パダワン(マスタはなんでいつも僕をひとりにするのかな …)
パダワン(僕のことが嫌いなのかな …)
パダワン(でも今日は Gopher君が一緒だから寂しくないし)
パダワン(ま、いっか)
パダワン「さてと、、」
パダワン「回すのはさっきやったからいいとして、、」
パダワン「軌道を丸く描くのはどうすればいいんだろ?」
パダワン「お! circle() ってメソッドがあんじゃん!」
パダワン「でも、これ x と y しか指定できないや …」
パダワン「P3D に描いたらどうなるんだろ?」
パダワンは Simulator.pde に以下のように追記し実行してみた。
...
void draw() {
background(255, 255, 255);
updateDevRoom();
gGalaxy.update();
gSun.update();
fill(192, 192, 255); // +++
circle(0, 0, 500); // +++
}
パダワン「そしたら、このマルを倒せばいいから …」
パダワン「えーと、親指が X で、人差し指が Y で、、」
パダワン「あっ!親指で回せばいいんだ!」
...
void draw() {
background(255, 255, 255);
updateDevRoom();
gGalaxy.update();
gSun.update();
rotateX(HALF_PI); // +++
fill(192, 192, 255);
circle(0, 0, 500);
}

パダワン「あは!簡単すぎて泣けてくる(笑)」
パダワン「そしたらあとはクラスを作るだけ!」
パダワン「えーと、」
パダワン「新規タブで OrbitalObject を作って、、」
// 円軌道を公転する天体
public class OrbitalObject extends CelestialObject {
private float mRadius; // 公転半径
private int mPeriod; // 公転周期(ミリ秒)
// コンストラクタ
// param parent 公転体の母星
// param imageName 画像のファイル名
// param w 公転体(ビルボード)の幅
// param radius 公転半径
// param period 公転周期(秒)
public OrbitalObject(CelestialObject parent, String imageName, int w, float radius, int period) {
super(imageName, w, 0, 0, 0);
mRadius = radius;
mPeriod = period * 1000;
parent.addChild(this); // 母星に自分を追加
}
// 座標変換して描画
public void update() {
updateOrbit();
super.update();
}
// 座標変換
protected void transform() {
int ms = millis();
float rd = TWO_PI * ms / mPeriod;
rotateY(rd);
translate(mRadius, 0, 0);
}
// 軌道を描画
protected void updateOrbit() {
pushMatrix();
rotateX(HALF_PI);
pushStyle();
noFill();
stroke(48, 48, 48);
strokeWeight(1);
circle(0, 0, mRadius * 2);
popStyle();
popMatrix();
}
}
パダワン「えーと、」
-
public OrbitalObject(...) {...}
コンストラクタの引数で、ママと半径と速さを指定できるようにしたった。-
super(imageName, w, 0, 0, 0);
とりあえず、場所は (0, 0, 0) でごまかして、、 -
mPeriod = period * 1000;
あとで計算めんどいから中では「ミリ秒」で持っとくけど、寛大な僕は引数では「秒」で指定するようにしたった。 -
parent.addChild(this);
めんどいから、ここでママに追加しちゃおっと。
フィールドにママ持っとく必要ないし!
-
-
public void update() {...}
スーパーさんを上書きしたった-
updateOrbit();
マルだけ自分で描いといて、、 -
super.update();
あとはスーパーさんにお任せっ!
-
-
protected void updateOrbit() {...}
マルを描くよん!-
rotateX(HALF_PI);
パイの半分 90 度~♪ もう完璧に覚えたわ(笑) -
circle(0, 0, mRadius * 2);
マルは直径が必要だから、2 倍したった!
-
4 時 50 分|SolarSystem クラス
パダワン「そしたら、太陽一家のクラスもあった方がいいよなぁ …」
パダワン「こんな感じかな?」
SolarSystem クラス
| カテゴリ | 項目 | 説明 |
|---|---|---|
| class | SolarSystem | 太陽系クラス。太陽系の星々を表示する。太陽は CelestialObject、惑星と衛星は OrbitalObject クラスで実装する。 |
| method | update | すべての星を描画する。 |
パダワン「えーと、」
パダワン「新規タブで SolarSystem を作って、」
パダワン「星の大きさと回り方はわかんないから」
パダワン「パラメータはひとまず適当に、、」
// 太陽系クラス
public class SolarSystem {
private CelestialObject mSun; // 太陽
// コンストラクタ
public SolarSystem() {
mSun = new CelestialObject("gp_sun.png", 200, 0, 0, 0);
OrbitalObject earth =
new OrbitalObject(mSun, "gp_earth.png", 50, 333, 16); // 地球
new OrbitalObject(earth,"gp_moon.png", 25, 77, 7); // 月
new OrbitalObject(mSun, "gp_mercury.png", 30, 111, 8); // 水星
new OrbitalObject(mSun, "gp_venus.png", 40, 222, 12); // 金星
new OrbitalObject(mSun, "gp_mars.png", 40, 444, 20); // 火星
new OrbitalObject(mSun, "gp_jupiter.png",170, 555, 24); // 木星
new OrbitalObject(mSun, "gp_saturn.png", 160, 666, 28); // 土星
new OrbitalObject(mSun, "gp_uranus.png", 80, 777, 32); // 天王星
new OrbitalObject(mSun, "gp_neptune.png", 70, 888, 36); // 海王星
}
// すべての星を座標変換して描画
public void update() {
mSun.update();
}
}
パダワン「お、こんだけでいいのか …」
パダワン「月から下は、変数いらねーし(笑)」
パダワン「あとは、Simulator タブの書き直しだっ …」
Galaxy gGalaxy;
//CelestialObject gSun; // ---
SolarSystem gSolarSystem; // +++
void setup() {
gGalaxy = new Galaxy();
gSolarSystem = new SolarSystem(); // +++
//gSun = new CelestialObject("gp_sun.png", 300, 0, 0, 0); // ---
//CelestialObject earth = new CelestialObject("gp_earth.png", 100, -200, 0, 0); // ---
//CelestialObject jupiter = new CelestialObject("gp_jupiter.png", 100, 200, 0, 0); // ---
//CelestialObject saturn = new CelestialObject("gp_saturn.png", 100, 0, 0, -200); // ---
//CelestialObject uranus = new CelestialObject("gp_uranus.png", 100, 0, 0, 200); // ---
//gSun.addChild(earth); // ---
//gSun.addChild(jupiter); // ---
//gSun.addChild(saturn); // ---
//gSun.addChild(uranus); // ---
size(1920, 1080, P3D);
hint(ENABLE_DEPTH_SORT);
frameRate(24);
}
void draw() {
background(255, 255, 255);
updateDevRoom();
gGalaxy.update();
gSolarSystem.update(); // +++
//gSun.update(); // ---
//rotateX(HALF_PI); // ---
//fill(192, 192, 255); // ---
//circle(0, 0, 500); // ---
}
パダワン「あは!簡単すぎて、鳥肌(笑)」

午前 5 時|実装を進める
5 時 00 分|惑星系の情報を整理する
パダワン「あっ! マスタからデータが届いてる!」
その情報をしばらく眺めたあと、パダワンは太陽系に所属する天体のうち、大きいものから順に 18 個の星を並べてみた。
| 天体 | 母星 | 平均直径 | 平均公転半径 | 公転周期 |
|---|---|---|---|---|
| 太陽 | 1,392,000 km | |||
| 木星 | 太陽 | 139,822 km | 778,412,010 km | 4,332.43 日 |
| 土星 | 太陽 | 116,464 km | 1,426,725,400 km | 10,786.62 日 |
| 天王星 | 太陽 | 50,724 km | 2,870,990,000 km | 30,773.41 日 |
| 海王星 | 太陽 | 49,244 km | 4,495,060,000 km | 60,189.55 日 |
| 地球 | 太陽 | 12,742 km | 149,597,871 km | 365.25 日 |
| 金星 | 太陽 | 12,104 km | 108,208,930 km | 224.70 日 |
| 火星 | 太陽 | 6,780 km | 227,920,000 km | 686.98 日 |
| ガニメデ | 木星 | 5,262 km | 1,070,400 km | 7.16 日 |
| タイタン | 土星 | 5,152 km | 1,221,865 km | 15.95 日 |
| 水星 | 太陽 | 4,879 km | 57,910,000 km | 87.97 日 |
| カリスト | 木星 | 4,821 km | 1,882,700 km | 16.69 日 |
| イオ | 木星 | 3,643 km | 421,700 km | 1.77 日 |
| 月 | 地球 | 3,474 km | 384,400 km | 27.33 日 |
| エウロパ | 木星 | 3,122 km | 671,100 km | 3.55 日 |
| トリトン | 海王星 | 2,707 km | 354,759 km | (逆行) 5.88 日 |
| 冥王星 | 太陽 | 2,370 km | 5,900,898,441 km | 90,487.28 日 |
| エリス | 太陽 | 2,326 km | 10,139,893,274 km | 203,824.11 日 |
パダワン「げっ! 数がおっきすぎて全然ピンとこない …」
そこでパダワンは、地球の直径を 50 px、公転周期を 60 秒とした場合の換算値を計算し、各天体と母星との関係を整理してみた。
| 恒星 | 惑星等 | 衛星 | 直径 | 公転半径 | 公転周期 |
|---|---|---|---|---|---|
| 太陽 | 5,462.25 px | ||||
| 水星 | 19.15 px | 227,240.62 px | 14.45 s | ||
| 金星 | 47.49 px | 424,615.17 px | 36.91 s | ||
| 地球 | 50.00 px | 587,026.65 px | 60.00 s | ||
| 月 | 13.63 px | 1,508.40 px | 4.49 s | ||
| 火星 | 26.60 px | 894,365.09 px | 112.85 s | ||
| 木星 | 548.67 px | 3,054,512.67 px | 711.69 s | ||
| イオ | 14.30 px | 1,654.76 px | 0.29 s | ||
| エウロパ | 12.25 px | 2,633.42 px | 0.58 s | ||
| ガニメデ | 20.65 px | 4,200.28 px | 1.18 s | ||
| カリスト | 18.92 px | 7,387.77 px | 2.74 s | ||
| 土星 | 457.01 px | 5,598,514.36 px | 1,771.93 s | ||
| タイタン | 20.22 px | 4,794.64 px | 2.62 s | ||
| 天王星 | 199.04 px | 11,265,853.08 px | 5,055.18 s | ||
| 海王星 | 193.23 px | 17,638,753.73 px | 9,887.40 s | ||
| トリトン | 10.62 px | 1,392.09 px | (逆行) 0.97 s | ||
| 冥王星 | 9.30 px | 23,155,307.02 px | 14,864.44 s | ||
| エリス | 9.13 px | 39,789,253.15 px | 33,482.40 s |
パダワン「これでも、でっかすぎる、、」
パダワン「でも、マスタの言ってたとおり」
パダワン「月って星は 4 個分で地球と同じくらいになるのか …」
パダワン「ママに比べて、でかいんだなぁ」
パダワン(僕もおっきくなりたいし、、)
パダワン(ママがほしい …)
パダワン「あとは …」
パダワン「イオって星が めちゃっ速なのと、」
パダワン「トリトンって星は逆回りなのか、、」
パダワン「かっけー!」
5 時 10 分|バグを直す
天体のパラメータをどうするかでパダワンが頭を悩ませていると、そこにひとりの老紳士が姿を現した。
最高議長「やあ!パダワン君!」
最高議長「君の噂はかねがね、グランド・マスターから聞いているよ」
最高議長「どうだね? 順調かね?」
パダワン「あ? ん? おじさん誰???」
最高議長「おお!これは申し遅れてすまなかった …」
最高議長「私は元老院の最高議長を務めているただの老いぼれだよ(笑)」
パダワン「げっ!最高議長???」
パダワン「それってグランド・マスタより偉い人じゃね?!」
パダワン「ん? おじさん、今、偉い人達会議じゃないの?」
最高議長「議会はついさっき、無事に閉会したんだ」
パダワン「そっか …」
パダワン「戦争が始まっちゃうの?」
最高議長「できれば戦争はすべきではない」
最高議長「だが、時として」
最高議長「命より大切なものを守らねばならないことがある」
最高議長「そういう時代に戦争は必要になるのだよ」
パダワン「ふーん …」
パダワン「僕にはよくわかんないや(笑)」
最高議長「ところで、シミュレーターの進捗状況はどうだね?」
パダワン「余裕! あとは画像を差し替えるくらいかな …」
最高議長「おお!すばらしい!」
最高議長「それならパダワン君お手製のセーバーを」
最高議長「是非見せてもらえないか?」
パダワン「お安い御用さ!」
パダワン「でも、おじさん殺陣できんの???」
最高議長はしばらくセーバーを眺めたあとで、ゆっくりと口を開いた。
最高議長「なるほど、よく書けているが、、」
最高議長「2 つほど修正した方が良さそうだ」
パダワン「え?バグ見つけたの? おじさんすげー!」
最高議長「ひとつは、開始時点の各惑星や衛星の座標だ」
最高議長「みな角度 0 からスタートしているから」
最高議長「惑星直列の状態から始まってしまうね」
最高議長「それは少し不自然だから、」
最高議長「乱数で開始地点を散らした方が良いだろうね」
パダワン「なるほど …」
最高議長「もうひとつの問題は、」
最高議長「公転体の座標を決める式だ」
...
float rd = TWO_PI * ms / mPeriod;
...
パダワン「ええっ???」
パダワン「これのどこがいけないんだろ?」
パダワン「えーと、、」
パダワン「mPeriod は1周にかかる時間(ミリ秒)で」
パダワン「ms は過ぎた時間(ミリ秒)だから、」
パダワン「例えば、一周に 100 かかるところを」
パダワン「50 かかったら一周のちょうど半分 (0.5) だから、」
パダワン「一周 360°(TWO_PI) の半分は 180°(PI) で合ってるし、」
パダワン「一周に 100 かかるところを」
パダワン「150 かかったら一周半 (1.5) だから、」
パダワン「一周 360°(TWO_PI) に半分足して、540°、、」
パダワン「合ってんじゃん!!!」
パダワン「360°超えても大丈夫ってマスタ言ってたし …」
パダワン「えー?! 完璧なはず、、」
最高議長「パダワン君」
最高議長「考え方はそれで間違っていないのだよ」
最高議長「問題は浮動小数点数を使っているところなんだ」
パダワン「えー???」
パダワン「でも Processing は普通に float 使ってるし」
パダワン「int とかよりおっきい数でもへっちゃらじゃん!!」
最高議長「確かに、取り扱える範囲は float の方が広いが、」
最高議長「その分、精度が犠牲になってしまうんだよ」
最高議長「360 とか 720 とか、数が小さなうちは」
最高議長「(有効数字が少なくても済むうちは)それでもいいんだ」
最高議長「だが、仮数部が扱える有効数字は 7 桁程度だから」
最高議長「それを超える厳密な表現はできないのだよ」
最高議長「角度を求める式では、」
最高議長「結局は 360°(もしくは 2π)で割ったときの余り、」
最高議長「つまり精度が大事になるのだ」
最高議長「そして浮動小数点数は、、」
最高議長「国家と似ている …」
最高議長「人口が少ないうちはいい …」
最高議長「だが、人口がある程度増えてしまったら、、」
最高議長「少数の犠牲はやむを得ないのだよ!!!」
最高議長「わかるかね? パダワン君 …」
最高議長「わ・か・る・か・ね?!!」
最高議長「パ・ダ・ワ・ン・君!!!」
パダワン「お、おじさん、、」
パダワン「ちょっと怖い …」
最高議長「おお、すまない、すまない、、」
最高議長「議会が終わったばかりで」
最高議長「まだ興奮が冷めていないようだ(笑)」
最高議長「OrbitalObject.pde に次のように追記してみなさい」
...
protected void transform() {
//int ms = millis(); // --- コメントアウト
int ms = millis() + 1000000000; // +++ 追記
float rd = TWO_PI * ms / mPeriod;
rotateY(rd);
translate(mRadius, 0, 0);
}
...
最高議長「これはセーバーを起動してから 10 億ミリ秒後、」
最高議長「つまり約 11 日半経過したときの状態を」
最高議長「意図的に作り出すものだ」
パダワンは実行ボタンをクリックした。
パダワン「げげげっ!!!」
パダワン「動きがカクカクしてる!!!」
最高議長「 [ファイル][新規] を選択し、」
最高議長「新しいスケッチを開いて次のように入力してみなさい」
int period = 3600; // 周期は3600ミリ秒(10ミリ秒ごとに1°進む)
int[] startingTimes = { // 開始時のミリ秒値を格納する配列
0, // 状況 a. 1周目
36000000, // 状況 b. 10,001周目
1000000800, // 状況 c. 277,779周目
};
println("a.\tb.\tc.");
println("---\t---\t---");
//3種類の時間経過状況で、10ミリ秒刻みで角度がどのように増えていくか
for (int n = 0; n < 300; n += 10) {
for (int start: startingTimes) {
int ms = start + n;
int rd = round(degrees(TWO_PI * ms / period)) % 360;
print(rd + "°\t");
}
println();
}
最高議長「これは、今のロジックで」
最高議長「3600 ミリ秒周期の公転体の計算をすると、」
最高議長「状況 a. → セーバー開始直後(つまり 1 周目)、」
最高議長「状況 b. → ちょうど 10,001 周目、」
最高議長「状況 c. → ちょうど 277,779 周目の」
最高議長「3 種類の状況で 10 ミリ秒づつ刻んだ時に」
最高議長「角度がどのように増えていくかを表示するものだよ」
パダワン「3600 ミリ秒で 1 周だから、」
パダワン「10 ミリ秒ごとに 1° づつ増えていくはずだよ!」
最高議長「では結果を見てみよう」
パダワン「うわっ、状況 c. が!!!」
a. b. c.
--- --- ---
0° 0° 352°
1° 1° 0°
2° 2° 0°
3° 3° 0°
4° 4° 0°
5° 5° 0°
6° 6° 0°
7° 7° 8°
8° 8° 8°
9° 9° 8°
10° 10° 8°
11° 11° 8°
12° 12° 8°
13° 13° 8°
14° 14° 8°
15° 15° 8°
16° 16° 8°
17° 17° 8°
18° 18° 8°
19° 19° 8°
20° 20° 16°
21° 21° 16°
22° 22° 16°
23° 23° 16°
24° 24° 16°
25° 25° 16°
26° 26° 32°
27° 27° 32°
28° 28° 32°
29° 29° 32°
パダワン「数字が飛び飛びじゃん!」
パダワン「げげっ!どーすりゃいーんだ???」
最高議長「変数 ms には、ms / PERIOD の」
最高議長「商と剰余が含まれているのはわかるかな?」
パダワン「えーと、例えば3 周半回った時は、」
パダワン「割り算の答えが3 周にかかった時間で」
パダワン「割り算の余りが半分にかかった時間になるけど …」
最高議長「そうだな」
最高議長「ms には3 周半分の時間が含まれている」
最高議長「だが角度を算出するときに大事なのは、」
最高議長「3 周分の時間ではなく」
最高議長「残りの半周分の時間なのだよ」
最高議長「だから、この半周分の剰余を」
最高議長「浮動小数点数の演算で精度が犠牲になる前に、」
最高議長「精度が保たれる整数型で求めておいた方が良いであろうな」
パダワン「あ!そっか!」
パダワンは以下のようにセーバーを書き換えた。
...
//int rd = round(degrees(TWO_PI * ms / period)) % 360; // 修正前
int rd = round(degrees(TWO_PI * (ms % period) / period)); // 修正後
...
パダワン「おお! 完璧!!!」
a. b. c.
--- --- ---
0° 0° 0°
1° 1° 1°
2° 2° 2°
3° 3° 3°
4° 4° 4°
5° 5° 5°
6° 6° 6°
7° 7° 7°
8° 8° 8°
9° 9° 9°
10° 10° 10°
11° 11° 11°
12° 12° 12°
13° 13° 13°
14° 14° 14°
15° 15° 15°
16° 16° 16°
17° 17° 17°
18° 18° 18°
19° 19° 19°
20° 20° 20°
21° 21° 21°
22° 22° 22°
23° 23° 23°
24° 24° 24°
25° 25° 25°
26° 26° 26°
27° 27° 27°
28° 28° 28°
29° 29° 29°
最高議長「あとは、millis() の戻り値が int 型だから」
最高議長「セーバー開始から 2,147,483,648 ミリ秒経過後、」
最高議長「つまり約 25 日経過した時点で」
最高議長「オーバーフローが発生することが予想できるが、」
最高議長「今回はそこまで考慮しなくて良いよ!」
パダワン「うわっ! おじさん優しい!!!」
パダワン「そしたら、OrbitalObject を直して、」
パダワン「最初からばらばらになるようにするのと、」
パダワン「カクカクしないようにするぞ!」
...
public class OrbitalObject extends CelestialObject {
private float mRadius; // 公転半径
private int mPeriod; // 公転周期(ミリ秒)
private float mStart; // +++ 追記
...
public OrbitalObject(CelestialObject parent, String imageName, int w, float radius, int period) {
...
mPeriod = period * 1000;
mStart = random(TWO_PI); // +++ 追記
parent.addChild(this); // 母星に自分を追加
}
...
protected void transform() {
//int ms = millis(); // 後で戻す
int ms = millis() + 1000000000; // 後で消す
//float rd = TWO_PI * ms / mPeriod; // --- 削除
float rd = mStart + TWO_PI * (ms % mPeriod) / mPeriod; // +++ 追記
...
}
...
}
パダワン「最初からバラバラになったし」
パダワン「カクカクしなくなった!」
パダワンは最終的に transform() メソッドを以下のように整理して、OrbitalObject の殺陣を終えた。
...
// 座標変換
protected void transform() {
int ms = millis();
float rd = mStart + TWO_PI * (ms % mPeriod) / mPeriod;
rotateY(rd);
translate(mRadius, 0, 0);
}
...
パダワン「おじさんすげー!」
パダワン「ありがとー!」
5 時 20 分|画像を加工する
パダワン「おっ!マスタがなんか送ってきた!」
パダワンへ
太陽系の天体の画像を集めたから送付する
私はこれからグランド・マスターと話があるから、ひとりで次の作業をしておきなさい
・銀河系の星々は Gimp を使って自分でパーティクルを作る
・太陽系の天体は、画像のライセンスを確認した上で Gimp で加工する。
・できあがった画像をセーバーへ取り込む
最高議長「私は後ろで見ているから、気にせず作業を続けなさい」
Gimp でパーティクルを作る
パダワンはパーティクル画像を作成するために Gimp を立ち上げた。
パダワン「えーと、まずは背景が黒い画像を作って、」
パダワン「ライト効果でやってみっか!」
パダワン「色を選んだり、位置を調整して [OK] 押したら、、」
パダワン「ん? でもこれ、、」
パダワン「後ろを透明にするのはどーすんだ???」
最高議長「その場合は、、」
最高議長「色を透明度に...で加工すれば良いであろう」
最高議長「ただし、もしアルファチャンネルがない画像であれば」
最高議長「先に、2 つ上のメニューアイテムである」
最高議長「アルファチャンネルの追加を選んでおく必要があるぞ」
パダワン「おおっ!!!」
パダワン「おじさんすげー!!!」
パダワン「じゃあ、あとは残りの 4 色も」
パダワン「おんなじように作って、、」
パダワン「銀河は星がいっぱいだから」
パダワン「画像サイズをちっちゃくしてから保存するのを」
パダワン「忘れずに! っと …」
ライセンスに気を付ける
パダワン「えーと、次はライセンスかぁ …」
パダワン「ええっ???」
パダワン「画像って勝手に使っちゃいけないの???」
画像等のライセンスの分類
| 記号 | 主張 | 説明 |
|---|---|---|
| PDM | public domain | Public Domain Mark 原作者が権利を放棄したか、保護期間が終了していることを明示するマーク。 ただし、パブリックドメインとなった作品でも以下の点に注意。 ・著作者人格権が存在しているため、作者の人格を中傷するような作品の改変は禁止されている。 ・商標権が存在しているものは、それを侵害する可能性がある。 ・人物などの写真の場合は、肖像権侵害やパブリシティ権侵害となる恐れがある。 |
| CC0 | public domain | いかなる権利も保有しないことを宣言するマーク。 PDM との違い |
| CC | Some rights reserved | 限定された権利を主張するもの。 クリエイティブ・コモンズ・ライセンス |
| Ⓒ | All rights reserved | 著作権を主張するもの。 |
パダワン「public domain ってのが使いやすいのかと思ったけど、、」
パダワン「いろいろ気を付けなきゃならないんだなぁ …」
パダワン「それで、CC ってのを更に詳しくみてみると、」
パダワン「4 種類の条件ってのがあって、、」
CCライセンスの種類
| マーク | 意味 |
|---|---|
| BY | 作品のクレジットを表示すること |
| SA | 元の作品と同じ組み合わせのCCライセンスで公開すること |
| ND | 元の作品を改変しないこと |
| NC | 営利目的での利用をしないこと |
パダワン「で、これを組み合わせた 6 種類のライセンスがある、、」
パダワン「うげっ! ややこしい!!!」
パダワン「あ、でも今回関係あるのはこの 2 種類なのか!」
CCライセンスの組み合わせ
| マーク | 意味 |
|---|---|
| CC BY | 原作者のクレジットを表示することを条件に、改変および、営利目的での二次利用が許されるライセンス。 |
| CC BY-SA | 原作者のクレジットを表示し、改変した場合は CC BY-SA で公開することを条件に、営利目的での二次利用も許可されるライセンス。 |
| その他 | CC BY-ND、CC BY-NC、CC BY-NC-SA、CC BY-NC-ND などがある。 |
パダワン「で、マスタが送ってくれた画像のライセンスは、、」
加工前の画像リスト
| 天体 | 画像 | ライセンス | 出典 |
|---|---|---|---|
| 太陽 |  |
Created by NASA (public domain) |
Wikimedia Commons |
| 水星 |  |
Created by NASA (public domain) |
Wikimedia Commons |
| 金星 |  |
Created by NASA (public domain) |
Wikimedia Commons |
| 地球 |  |
Created by NASA (public domain) |
Wikimedia Commons |
| 月 |  |
Luc Viatour (CC BY-SA 3.0) |
Wikimedia Commons |
| 火星 |  |
ESA & MPS for OSIRIS Team MPS/UPD/LAM/IAA/RSSD/ INTA/UPM/DASP/IDA (CC BY-SA IGO 3.0) |
Wikimedia Commons |
| 木星 |  |
Created by NASA (public domain) |
Wikimedia Commons |
| イオ |  |
Created by NASA (public domain) |
Wikimedia Commons |
| エウロパ | 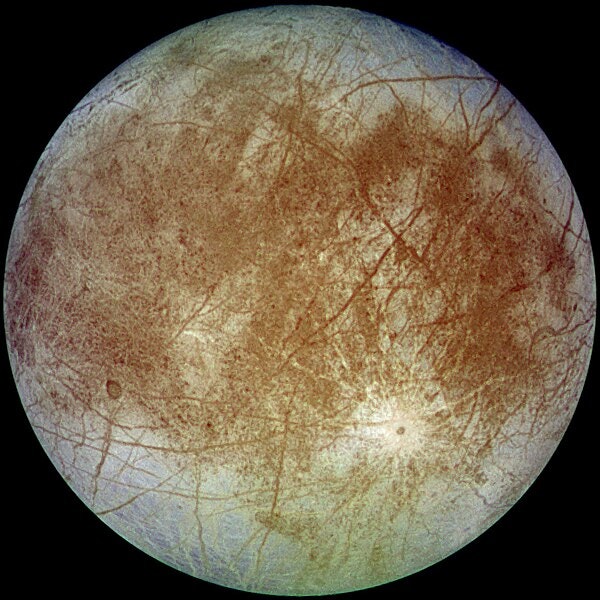 |
Created by NASA (public domain) |
Wikimedia Commons |
| ガニメデ |  |
Created by NASA (public domain) |
Wikimedia Commons |
| カリスト |  |
Created by NASA (public domain) |
Wikimedia Commons |
| 土星 |  |
Created by NASA (public domain) |
Wikimedia Commons |
| タイタン |  |
Created by NASA (public domain) |
Wikimedia Commons |
| 天王星 |  |
Created by NASA (public domain) |
Wikimedia Commons |
| 海王星 |  |
WolfmanSF (CC BY 2.0) |
Wikimedia Commons |
| トリトン |  |
Created by NASA (public domain) |
Wikimedia Commons |
| 冥王星 |  |
Created by NASA (public domain) |
Wikimedia Commons |
| エリス |  |
Created by NASA (public domain) |
Wikimedia Commons |
パダワン「なるほど、注意しなきゃ!」
Gimp で背景を透明にする
パダワン「そしたら、お星さまの背景を透明にするぞ」
パダワン「画像を開いたら、アルファチャンネルを追加して、、」
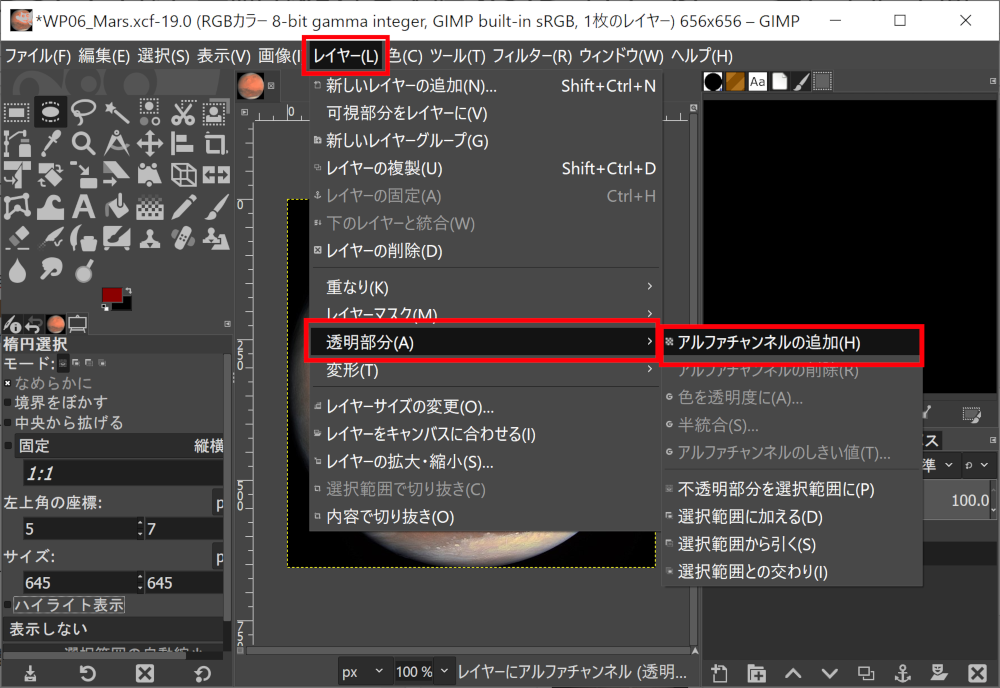
パダワン「楕円選択ツールを選んで、」
パダワン「ドラッグドロップで範囲を指定したら、、」
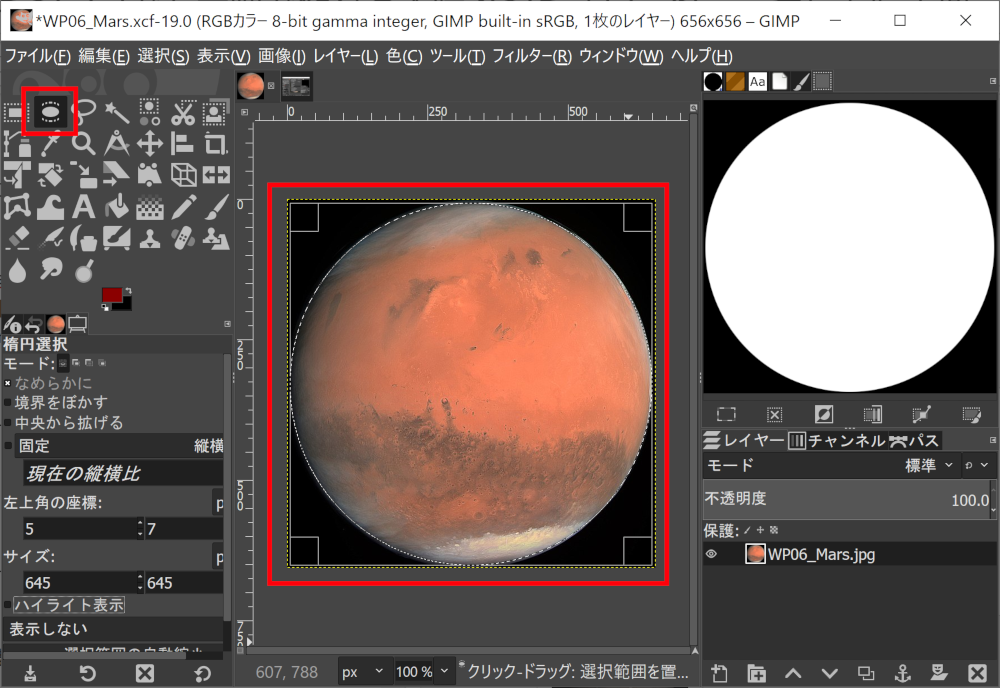
パダワン「消去する」
パダワン「で、これは DELETE キーでも消えますよ!っと …」
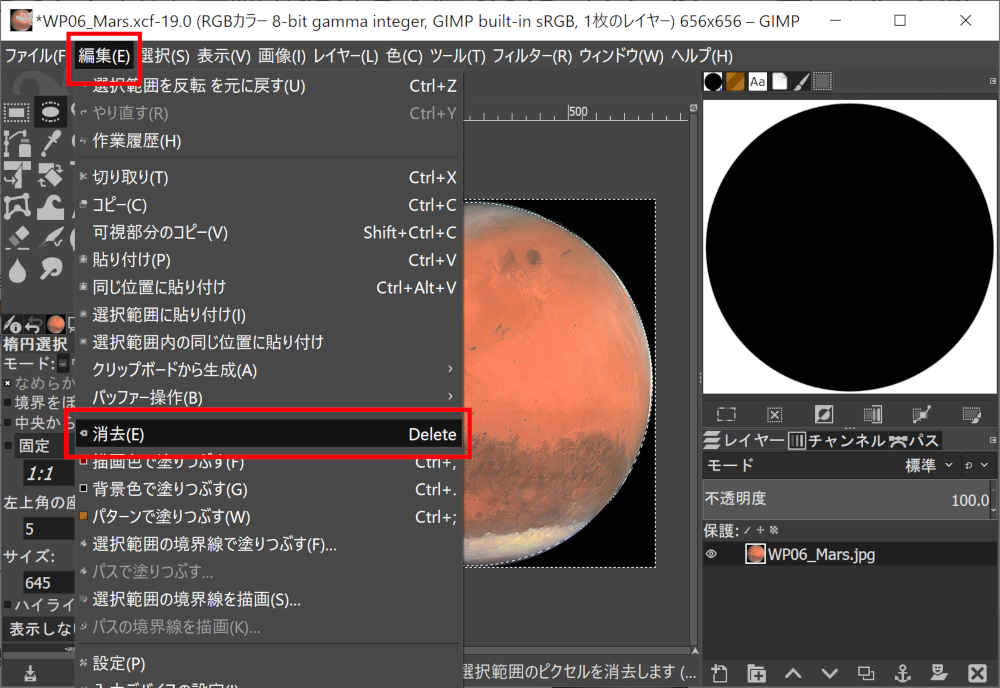
パダワン「あとは、名前を付けてエクスポートで、」
パダワン「拡張子を .png で保存すればオッケーですよ!っと …」
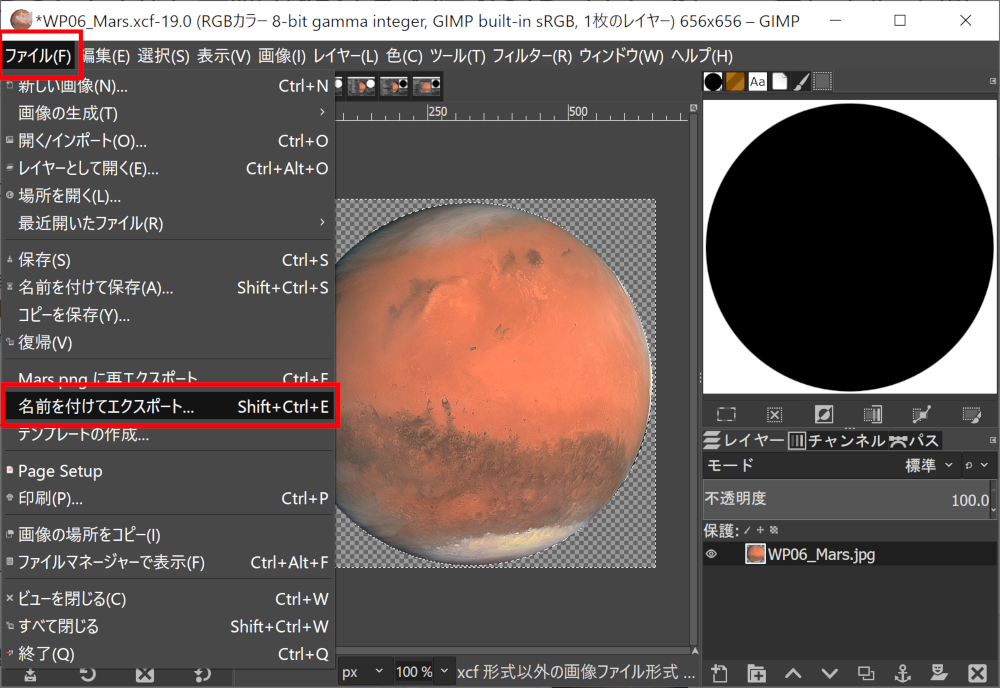
最高議長「おお!ひとつ言い忘れていた …」
最高議長「さっきのパーティクルの画像もそうであるが、」
最高議長「Gimp で作成した画像を Processing で開こうとすると」
最高議長「エラーになることがあるから、その場合は、」
最高議長「エクスポートのオプションで」
最高議長「赤枠のあたりを調整してみるといいだろう」
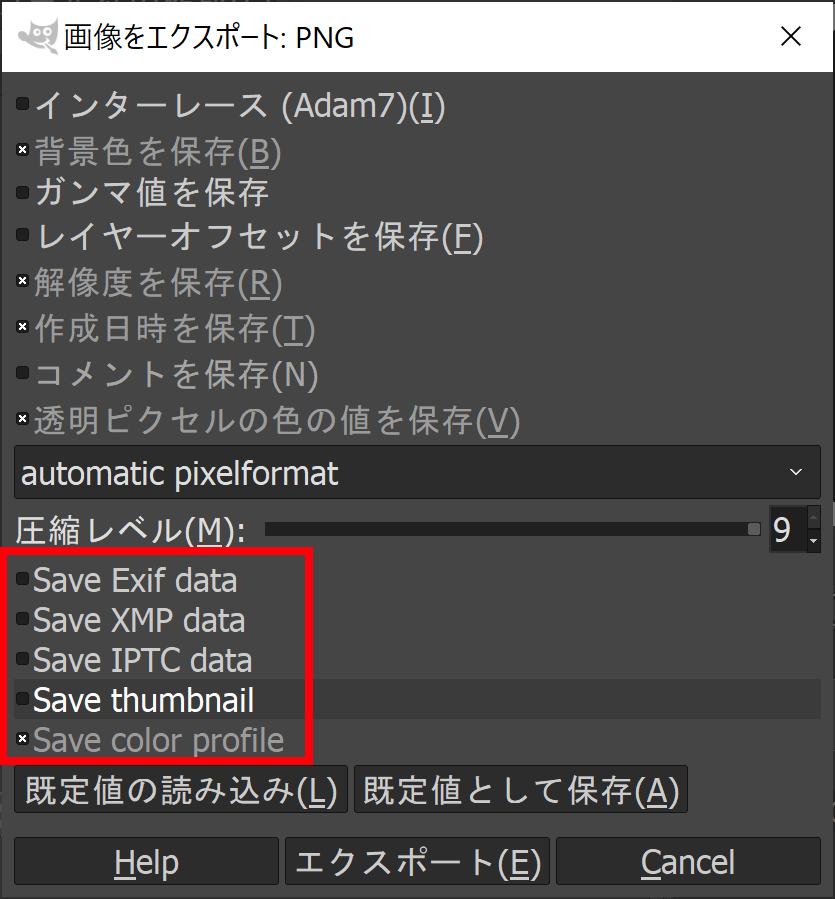
パダワンは最終的に以下の画像を作成した。
加工後の画像リスト
|天体|加工画像|オリジナル画像
のライセンス|オリジナル
画像の出典
|:-:|:-:|:-:|:-:|:-:
|太陽|Sun.png |Created by NASA
|Created by NASA
(public domain) |Wikimedia
Commons
|水星|Mercury.png |Created by NASA
|Created by NASA
(public domain) |Wikimedia
Commons
|金星|Venus.png |Created by NASA
|Created by NASA
(public domain) |Wikimedia
Commons
|地球|Earth.png |Created by NASA
|Created by NASA
(public domain) |Wikimedia
Commons
|月|Moon.png |Luc Viatour
|Luc Viatour
(CC BY-SA 3.0)|Wikimedia
Commons
|火星|Mars.png |ESA & MPS for OSIRIS Team
|ESA & MPS for OSIRIS Team
MPS/UPD/LAM/IAA/RSSD/
INTA/UPM/DASP/IDA
(CC BY-SA IGO 3.0)|Wikimedia
Commons
|木星|Jupiter.png |Created by NASA
|Created by NASA
(public domain) |Wikimedia
Commons
|イオ|Io.png |Created by NASA
|Created by NASA
(public domain) |Wikimedia
Commons
|エウロパ|Europa.png |Created by NASA
|Created by NASA
(public domain) |Wikimedia
Commons
|ガニメデ|Ganymede.png |Created by NASA
|Created by NASA
(public domain) |Wikimedia
Commons
|カリスト|Callisto.png |Created by NASA
|Created by NASA
(public domain) |Wikimedia
Commons
|土星|Saturn.png |Created by NASA
|Created by NASA
(public domain) |Wikimedia
Commons
|タイタン|Titan.png |Created by NASA
|Created by NASA
(public domain) |Wikimedia
Commons
|天王星|Uranus.png |Created by NASA
|Created by NASA
(public domain) |Wikimedia
Commons
|海王星|Neptune.png |WolfmanSF
|WolfmanSF
(CC BY 2.0)|Wikimedia
Commons
|トリトン|Triton.png |Created by NASA
|Created by NASA
(public domain) |Wikimedia
Commons
|冥王星|Pluto.png |Created by NASA
|Created by NASA
(public domain) |Wikimedia
Commons
|エリス|Eris.png |Created by NASA
|Created by NASA
(public domain) |Wikimedia
Commons
|白い恒星|WhiteStar50.png |Created by y-bash|本稿|
|Created by y-bash|本稿|
|青い恒星|BlueStar50.png |Created by y-bash|本稿|
|Created by y-bash|本稿|
|黄色い恒星|YellowStar50.png |Created by y-bash|本稿|
|Created by y-bash|本稿|
|オレンジの恒星|OrangeStar50.png |Created by y-bash|本稿|
|Created by y-bash|本稿|
|赤い恒星|RedStar50.png |Created by y-bash|本稿|
|Created by y-bash|本稿|
筆者は、ここに掲載した画像の貢献部分(画像加工)に関して権利を主張しません。
しかしながら、加工前のオリジナル作品には、改変を含む二次利用に関して条件が付与されているものがあります。例えば CC BY であればクレジットを表示する義務が生じ、CC BY-SA であれば加工作品にも同じライセンスで公開する義務が生じます。これらの利用に際してはオリジナル作品の条件に従うようにしてください。
また、パブリックドメインを謳っているものも含め、オリジナル作品の許諾者がその作品に関するすべての権利を有していることが必ずしも保証されている訳ではありません。
ここに掲載した画像をご利用になる場合は、これらの点を踏まえた上で、ご自身の責任において行ってください。
パダワン「ふぇっ、すげえ集中した!」
パダワン「疲れた …」
午前 6 時|完成させる
6 時 00 分|加工した画像を組み込む
パダワンは加工した画像を data フォルダに取り込み、IDE を開いた。
パダワン「さて、まずは銀河ちゃん、っと」
...
public Galaxy() {
// 画像配列の初期化
PImage[] images = new PImage[] {
//loadImage("gp_50_blue.png"), // ---
//loadImage("gp_50_white.png"), // ---
//loadImage("gp_50_yellow.png"), // ---
//loadImage("gp_50_orange.png"), // ---
//loadImage("gp_50_red.png"), // ---
loadImage("BlueStar50.png"), // +++
loadImage("WhiteStar50.png"), // +++
loadImage("YellowStar50.png"), // +++
loadImage("OrangeStar50.png"), // +++
loadImage("RedStar50.png"), // +++
};
...
パダワン「次は太陽一家さん、っと …」
public SolarSystem() {
//mSun = new CelestialObject("gp_sun.png", 200, 0, 0, 0); // 太陽 // ---
//OrbitalObject earth = // ---
// new OrbitalObject(mSun, "gp_earth.png", 50, 333, 16); // 地球 // ---
// new OrbitalObject(earth,"gp_moon.png", 25, 77, 7); // 月 // ---
//new OrbitalObject(mSun, "gp_mercury.png", 30, 111, 8); // 水星 // ---
//new OrbitalObject(mSun, "gp_venus.png", 40, 222, 12); // 金星 // ---
//new OrbitalObject(mSun, "gp_mars.png", 40, 444, 20); // 火星 // ---
//new OrbitalObject(mSun, "gp_jupiter.png",170, 555, 24); // 木星 // ---
//new OrbitalObject(mSun, "gp_saturn.png", 160, 666, 28); // 土星 // ---
//new OrbitalObject(mSun, "gp_uranus.png", 80, 777, 32); // 天王星 // ---
//new OrbitalObject(mSun, "gp_neptune.png", 70, 888, 36); // 海王星 // ---
mSun = new CelestialObject("Sun.png", 50, 0, 0, 0); // +++
OrbitalObject mercury = new OrbitalObject(mSun, "Mercury.png", 19, 227, 14); // +++
OrbitalObject venus = new OrbitalObject(mSun, "Venus.png", 47, 425, 37); // +++
OrbitalObject earth = new OrbitalObject(mSun, "Earth.png", 50, 587, 60); // +++
/* moon */new OrbitalObject(earth, "Moon.png", 13, 130, 4); // +++
OrbitalObject mars = new OrbitalObject(mSun, "Mars.png", 26, 894, 112); // +++
OrbitalObject jupiter = new OrbitalObject(mSun, "Jupiter.png",100,1527, 711); // +++
/* io */new OrbitalObject(jupiter, "Io.png", 14, 165, 1); // +++
/* europa */new OrbitalObject(jupiter, "Europa.png", 12, 263, 2); // +++
/* ganymede */new OrbitalObject(jupiter, "Ganymede.png",21, 420, 3); // +++
/* callisto */new OrbitalObject(jupiter, "Callisto.png",19, 590, 4); // +++
OrbitalObject saturn = new OrbitalObject(mSun, "Saturn.png", 100,2800, 886); // +++
/* titan */new OrbitalObject(saturn, "Titan.png", 20, 479, 3); // +++
OrbitalObject uranus = new OrbitalObject(mSun, "Uranus.png", 50,3755,1685); // +++
OrbitalObject neptune = new OrbitalObject(mSun, "Neptune.png", 50,4410,2472); // +++
/* triton */new OrbitalObject(neptune, "Triton.png", 11, 139, -1); // +++
OrbitalObject pluto = new OrbitalObject(mSun, "Pluto.png", 9,5789,3716); // +++
OrbitalObject eris = new OrbitalObject(mSun, "Eris.png", 9,6632,5580); // +++
}
パダワン「太陽系広すぎるから、」
パダワン「パラメタ適当にしたった(笑)」
パダワン「あとは、、」
パダワン「ユーティリティ邪魔だから見えないようにして、、」
パダワン「自動カメラも無効にして」
パダワン「自分で上から見下ろしますよ、っと …」
パダワン「あっ! 真っ暗にするのもお忘れなく …」
...
void setup() {
gGalaxy = new Galaxy();
gSolarSystem = new SolarSystem();
setDevRoomAutoCameraEnabled(false); // +++
setDevRoomVisible(false); // +++
size(1920, 1080, P3D);
hint(ENABLE_DEPTH_SORT);
frameRate(24);
}
void draw() {
camera( 100, -4000, 100, 0, 0, 0, 0, 1, 0);
//background(255, 255, 255); // ---
background(0, 0, 0); // +++
updateDevRoom();
gGalaxy.update();
gSolarSystem.update();
}
パダワン「だいたい動いてるみたい(笑)」
6 時 10 分|カメラを制御する
パダワン「でも、じっと見てるだけは寂しいなぁ …」
最高議長「それなら、、」
最高議長「自分で操作できるようにしてみたらどうだい?」
パダワン「ええっ? できんの!?」
最高議長「キーイベントを取り込むだけだから」
最高議長「難しくなんかないさ」
パダワン「おじさんすげー!!!」
パダワン「マスタなんて地味な技しか教えてくれないもん」
最高議長「そうなのかい?」
パダワン「うん。基礎が大事なんだって!」
パダワン「あとケチだし!」
最高議長「ははは」
最高議長「それなら私のところに来るかね?」
最高議長「私は銀河一のお金持ちだし、」
最高議長「君なら優秀な秘書官になってくれそうだからな(笑)」
パダワン「えーっ??? ほんとー?」
パダワン「すげーなぁ、おじさん」
パダワン「優しいし、かっこいい技、教えてくれるし、」
パダワン「しかもお金持ち!!!」
最高議長「なあパダワン君、、」
最高議長「君はもっと感情をストレートに表現した方が良い!」
パダワン「でも …」
パダワン「マスタはいつもいつも」
パダワン「感情を抑えろって …」
最高議長「それは古い考え方なのだよ …」
最高議長「今、時代は変わろうとしている」
最高議長「悲しい時は泣き叫び、」
最高議長「怒りたいときは、、」
最高議長「怒りを爆発させた方が良い!」
最高議長「その方が人間らしいとは思わんかね?!」
パダワン「うーん」
パダワン「難しいことはわなんないや!」
パダワン「あっ!キーイベントってどーやるんだっけ?」
最高議長「keyPressed() というメソッドを書いておけば」
最高議長「キーが押されたときに呼び出してくれるのだよ」
最高議長「あとは key と keyCode という変数を調べるだけなんだ」
Processing 公式サイト - リファレンス
keyPressed
key
keyCode
パダワン「なるほど!」
パダワン「文字を押したら、key にその文字が入ってきて、」
パダワン「→ とか押した場合は、keyCode に入ってくるんだね!」
パダワン「うぅ…」
パダワン「簡単すぎて泣けてくる(笑)」
パダワン「そしたら、新しいクラス作る!」
CameraController クラス
| カテゴリ | 項目 | 説明 |
|---|---|---|
| class | CameraController | カメラ制御クラス。キーボードでカメラの位置を制御する。カメラはワールド座標系の Y 軸を中心に、ZX 平面に平行な面の上で回転するものとし、常に原点(0,0,0)に視線を向けることとする。 |
| field | mRadius | 現在のカメラの軌道半径(ZX平面と平行な面) |
| field | mAngle | 現在のカメラの水平位置(軌道平面上の角度:deg) |
| field | mYCoord | 現在のカメラの垂直位置(Y座標:px) |
| field | mRadiusSpeed | カメラから見た前後方向の速度(mRadiusの変化量: px/sec) |
| field | mRotationalSpeed | カメラから見た左右方向の速度(mAngle の変化量:deg/sec) |
| field | mVerticalSpeed | カメラから見た上下方向の速度(mYCoordの変化量: px/sec) |
| field | mPrevMillis | 前回の millis() の値を保持 |
| method | left() | カメラ視点で見た場合に、 ・右へ移動中なら、右方向への変化量を下げ、 ・左へ移動中なら、左方向への変化量を上げる |
| method | right() | カメラ視点で見た場合に、 ・右へ移動中なら、右方向への変化量を上げ、 ・左へ移動中なら、左方向への変化量を下げる |
| method | up() | カメラ視点で見た場合に、 ・上昇中なら、上昇速度を上げ、 ・下降中なら、下降速度を下げる |
| method | down() | カメラ視点で見た場合に、 ・上昇中なら、上昇速度を下げ、 ・下降中なら、下降速度を上げる |
| method | forward() | カメラ視点で見た場合に、 ・前進中なら、前進速度を上げ、 ・後退中なら、後退速度を下げる |
| method | backward() | カメラ視点で見た場合に、 ・前進中なら、前進速度を下げ、 ・後退中なら、後退速度を上げる |
| method | printStatus() | カメラの現在の状態(現在位置やその変化量)をコンソールへ出力する |
| method | update() | カメラの位置を更新する |
パダワン「そしたら、新しいタブ作って (CameraController)、」
パダワン「セーバーを書きますよ、っと …」
// カメラ制御クラス
public class CameraController {
private float mRadius = 1000; // 現在のカメラの軌道半径(ZX平面と平行な面)
private float mAngle = 0; // 現在のカメラの水平位置(軌道平面上の角度:deg)
private float mYCoord = 0; // 現在のカメラの垂直位置(Y座標:px)
private int mRadiusSpeed = 0; // カメラから見た前後方向の速度(mRadiusの変化量: px/sec)
private int mRotationalSpeed = 0; // カメラから見た左右方向の速度(mAngle の変化量:deg/sec)
private int mVerticalSpeed = 0; // カメラから見た上下方向の速度(mYCoordの変化量: px/sec)
private int mPrevMillis = 0; // 前回の経過時間
// カメラの回転速度を下げる
// カメラ視点で見た場合、
// 右へ移動中なら、右方向への変化量を下げ、
// 左へ移動中なら、左方向への変化量を上げる
public void left() {
mRotationalSpeed -= 5;
printStatus();
}
// カメラの回転速度を上げる
// カメラ視点で見た場合、
// 右へ移動中なら、右方向への変化量を上げ、
// 左へ移動中なら、左方向への変化量を下げる
public void right() {
mRotationalSpeed += 5;
printStatus();
}
// カメラの上昇速度を上げる
// カメラ視点で見た場合、
// 上昇中なら、上昇速度を上げ、
// 下降中なら、下降速度を下げる
public void up() {
mVerticalSpeed -= 25;
printStatus();
}
// カメラの上昇速度を下げる
// カメラ視点で見た場合、
// 上昇中なら、上昇速度を下げ、
// 下降中なら、下降速度を上げる
public void down() {
mVerticalSpeed +=25;
printStatus();
}
// カメラの軌道半径の変化量を下げる
// カメラ視点で見た場合、
// 前進中なら、前進速度を上げ、
// 後退中なら、後退速度を下げる
public void forward() {
mRadiusSpeed -= 10;
printStatus();
}
// カメラの軌道半径の変化量を上げる
// カメラ視点で見た場合、
// 前進中なら、前進速度を下げ、
// 後退中なら、後退速度を上げる
public void backward() {
mRadiusSpeed += 10;
printStatus();
}
// カメラの現在の状態をコンソールへ出力する
public void printStatus() {
print("(R,A,V)=(");
print((int)mRadius + "px, " + (int)mAngle + "deg, " + (int)mYCoord + "px");
print(") (dR,dA,dV)=(");
print(mRadiusSpeed + "px/s, " + mRotationalSpeed + "deg/s, " + mVerticalSpeed + "px/s");
println(")");
}
// カメラの位置を更新する
public void update() {
int ms = millis();
if (ms/1000 != mPrevMillis/1000) printStatus(); // 1秒ごとにステータス表示
int dt = ms - mPrevMillis; // 時刻の変化量
mPrevMillis = ms; // 現在時刻を退避
// 軌道半径の更新
mRadius += mRadiusSpeed * dt / 1000.0;
mRadius = max(mRadius, 100.0); // 太陽にぶつかりそうになったら止める
if (mRadius==100.0) mRadiusSpeed = 0;
// 回転角の更新
mAngle += mRotationalSpeed * dt / 1000.0;
mAngle = mAngle % 360; // 0~360に収まるように正規化
if (mAngle < 0) mAngle += 360;
// 垂直位置の更新
mYCoord += mVerticalSpeed * dt / 1000.0;
float z = mRadius * cos(radians(mAngle));
float x = mRadius * sin(radians(mAngle));
float y = mYCoord;
camera(x, y, z, 0, 0, 0, 0, 1, 0);
}
}
パダワン「なんか、思ったより簡単に書けた!」
パダワン「あっ!でも、どのキー押したら」
パダワン「どう動くのか考えるの忘れてた(笑)」
キーアサイン
| キー | 右旋回中 | 左旋回中 |
|---|---|---|
| → | 速度を上げる | 速度を下げる |
| ← | 速度を下げる | 速度を上げる |
| キー | 上昇中 | 下降中 |
|---|---|---|
| ↑ | 速度を上げる | 速度を下げる |
| ↓ | 速度を下げる | 速度を上げる |
| キー | 前進中 | 後退中 |
|---|---|---|
| PgUp | 速度を上げる | 速度を下げる |
| PgDn | 速度を下げる | 速度を上げる |
パダワン「おっ! キーの定数が用意されてんじゃん!」
パダワン「→ は RIGHT で、」
パダワン「← は LEFT」
パダワン「↑ は UP で、」
パダワン「↓ は DOWN」
パダワン「あはは! 簡単すぎて泣けてく …」
パダワン「ん???」
パダワン「あれ? どんなにリファレンス見ても」
パダワン「PgUp と PgDn の定数が見つからねー」
最高議長「残念なことに、、」
最高議長「Processing では」
最高議長「それらの定数は用意されていないのだよ」
パダワン「えー???」
パダワン「でも定数が用意されてなきゃ」
パダワン「どんな値が入ってくるのか僕わかんないよ!」
最高議長「新規スケッチを開いて、」
最高議長「次のように書いてみなさい」
void setup() {
size(100, 100, P3D);
}
void draw() {
}
void keyPressed() {
println("key: " + key + ", keyCode: " + keyCode);
}
最高議長「動かしたら、何か入力してみるのだ!」
パダワン「おお! おじさん天才か?!」
key: a, keyCode: 65 # 'a' キーをプレス
key: b, keyCode: 66 # 'b' キーをプレス
key: c, keyCode: 67 # 'c' キーをプレス
key: d, keyCode: 68 # 'd' キーをプレス
key: e, keyCode: 69 # 'e' キーをプレス
key: f, keyCode: 70 # 'f' キーをプレス
key: g, keyCode: 71 # 'g' キーをプレス
key: ?, keyCode: 37 # [←] キーをプレス
key: ?, keyCode: 39 # [→] キーをプレス
key: ?, keyCode: 38 # [↑] キーをプレス
key: ?, keyCode: 40 # [↓] キーをプレス
key: , keyCode: 16 # [PgUp] キーをプレス
key: , keyCode: 11 # [PgDn] キーをプレス
...
パダワン「16 が PgUp で、11 が PgDn だー!」
パダワン「そしたら Simulator タブを書き換えよう!」
パダワン「それから、、」
パダワン「もうユーティリティも要らなそうだから」
パダワン「消しちゃおっと!」
Galaxy gGalaxy;
SolarSystem gSolarSystem;
CameraController gCameraController = new CameraController(); // +++
void setup() {
gGalaxy = new Galaxy();
gSolarSystem = new SolarSystem();
//setDevRoomAutoCameraEnabled(false); // ---
//setDevRoomVisible(false); // ---
size(1920, 1080, P3D);
hint(ENABLE_DEPTH_SORT);
frameRate(24);
}
void draw() {
//camera( 100, -4000, 100, 0, 0, 0, 0, 1, 0); // ---
background(0, 0, 0);
//updateDevRoom(); // ---
gCameraController.update(); // +++
gGalaxy.update();
gSolarSystem.update();
}
void keyPressed() { // +++
final int PAGE_UP = 16; // +++
final int PAGE_DOWN = 11; // +++
switch (keyCode) { // +++
case LEFT : gCameraController.left(); break; // +++
case RIGHT : gCameraController.right(); break; // +++
case UP : gCameraController.up(); break; // +++
case DOWN : gCameraController.down(); break; // +++
case PAGE_UP : gCameraController.forward(); break; // +++
case PAGE_DOWN : gCameraController.backward();break; // +++
} // +++
}
パダワン「よし!じゃー動かしてみよー!」
パダワン「おおっ!」
パダワン「完成かな???」
パダワン「完成じゃね!???」
パダワン「完成っしょー! これっ!!!」
最高議長「おめでとう。パダワン君!」
最高議長「あとは、テストをパスすれば良さそうだね」
最高議長「あ!あと、、」
最高議長「ひとつお願いがあるんだが、、」
最高議長「特別仕様の Gopher君を用意したから、」
最高議長「彼を月の周回軌道に乗せて」
最高議長「テストしておいてもらえるかな?」

パダワン「おおっ!かっけー!!!」
パダワン「てか、Gopher君どうしちゃったのぉ?!」
パダワン「目、充血しちゃったのぉ?!」
最高議長「じゃあ、私はそろそろ行かねばならないから、、」
最高議長「D.S.Gopher 君のことはみんなには内緒だよ」
最高議長「おじさんとパダワン君、2 人だけの秘密だ!」
パダワン「うん!わかった(笑)」
最高議長「ああ、それから、、」
最高議長「私の元へと、誘った件だが、、」
最高議長「本気で考えてみないか?!」
パダワン「おぉ!!!」
パダワン「おじさん、ありがとー!」
パダワン「おじさん、大好きー!!!」
パダワン「でも、今はやめとく …」
パダワン「マスタと、」
パダワン「銀河イチのセーバー使いになるって」
パダワン「約束したから!!!」
パダワン「じゃーね、おじさん!」
パダワン「優しくしてくれてありがとー!」
パダワン「あと、かっけー技も教えてくれて」
パダワン「ほんとにありがとー!」
6 時 50 分|シミュレーターの全コード
しばらくして、マスターはパダワンの元へ戻ってきた。
マスター「おお、寝てしまったのか、、」
マスター「でも、シミュレーターは無事完成したようだ!」
マスター「よく頑張ったな!」
マスター「さぞかし疲れただろう …」
マスター「今はゆっくり眠るんだ」
そう言って優しく微笑みながら、マスターはセーバーのレビューを始めた。
フォルダ構成
any-dir
Simulator
├── Simulator.pde
├── Billboard.pde
├── CelestialObject.pde
├── OrbitalObject.pde
├── Galaxy.pde
├── SolarSystem.pde
├── CameraController.pde
└── data
├── WhiteStar50.png
├── BlueStar50.png
├── YellowStar50.png
├── OrangeStar50.png
├── RedStar50.png
├── Sun.png
├── Mercury.png
├── Venus.png
├── Earth.png
├── Moon.png
├── Mars.png
├── Jupiter.png
├── Io.png
├── Europa.png
├── Ganymede.png
├── Callisto.png
├── Saturn.png
├── Titan.png
├── Uranus.png
├── Neptune.png
├── Triton.png
├── Pluto.png
└── Eris.png
ソースコード
Simulator.pde の全コードを展開
// 太陽系シミュレーター
Galaxy gGalaxy; // 銀河の星々
SolarSystem gSolarSystem; // 太陽系の星々
CameraController gCameraController =
new CameraController(); // カメラ制御
void setup() {
gGalaxy = new Galaxy();
gSolarSystem = new SolarSystem();
size(1920, 1080, P3D);
hint(ENABLE_DEPTH_SORT);
frameRate(24);
}
void draw() {
background(0, 0, 0);
gCameraController.update();
gGalaxy.update();
gSolarSystem.update();
}
void keyPressed() {
final int PAGE_UP = 16; // PgUp キー
final int PAGE_DOWN = 11; // PgDn キー
switch (keyCode) {
case LEFT : gCameraController.left(); break;
case RIGHT : gCameraController.right(); break;
case UP : gCameraController.up(); break;
case DOWN : gCameraController.down(); break;
case PAGE_UP : gCameraController.forward(); break;
case PAGE_DOWN : gCameraController.backward();break;
}
}
Billboard.pde の全コードを展開
// ビルボードクラス
public class Billboard {
private PImage mImage; // ビルボードに貼り付ける画像
private int mWidth; // ビルボードの幅
private int mHeight; // ビルボードの高さ
private float mX; // ビルボードのX座標
private float mY; // ビルボードのY座標
private float mZ; // ビルボードのZ座標
// コンストラクタ
// param imageName: 貼り付ける画像のファイル名
// param w : ビルボードの幅
// param x : ビルボードのX座標
// param y : ビルボードのY座標
// param z : ビルボードのZ座標
public Billboard(String imageName, int w, float x, float y, float z) {
this( loadImage(imageName), w, x, y, z);
}
// コンストラクタ
// param image: 貼り付ける画像
// param w : ビルボードの幅
// param x : ビルボードのX座標
// param y : ビルボードのY座標
// param z : ビルボードのZ座標
public Billboard(PImage image, int w, float x, float y, float z) {
mImage = image;
mWidth = w;
mHeight = w * mImage.height / mImage.width; // 高さは画像の縦横比から計算
mX = x;
mY = y;
mZ = z;
}
// 座標変換して描画
public void update() {
pushMatrix();
transform();
turnToCamera();
drawSelf();
popMatrix();
}
// 座標変換
protected void transform() {
translate(mX, mY, mZ);
}
// 描画
protected void drawSelf() {
float hw = mWidth / 2;
float hh = mHeight / 2;
float iw = mImage.width;
float ih = mImage.height;
pushStyle();
noStroke();
beginShape();
texture(mImage);
vertex(-hw, -hh, 0, 0, 0);
vertex( hw, -hh, 0, iw, 0);
vertex( hw, hh, 0, iw, ih);
vertex(-hw, hh, 0, 0, ih);
endShape();
popStyle();
}
// カメラ方向に姿勢変更
protected void turnToCamera() {
PMatrix3D m = (PMatrix3D)g.getMatrix();
m.m00 = m.m11 = m.m22 = 1;
m.m01 = m.m02 = m.m10 = m.m12 = m.m20 = m.m21 = 0;
resetMatrix();
applyMatrix(m);
}
}
CelestialObject.pde の全コードを展開
// 天体クラス(子がいれば一緒に描画)
public class CelestialObject extends Billboard {
private ArrayList<Billboard> mChildren = null; // 子供リスト
// コンストラクタ
// param imageName 画像ファイル名
// param w 天体(ビルボード)の幅
// param x 天体(ビルボード)のX座標
// param y 天体(ビルボード)のY座標
// param z 天体(ビルボード)のZ座標
public CelestialObject(String imageName,
int w, float x, float y, float z) {
super(imageName, w, x, y, z);
}
// 子供を追加する
public void addChild(Billboard child) {
if (mChildren == null) {
mChildren = new ArrayList<Billboard>();
}
mChildren.add(child);
}
// 座標変換して描画(オーバーライド)
public void update() {
pushMatrix();
transform();
pushMatrix();
turnToCamera();
drawSelf(); // 自分を描画
popMatrix();
updateChildren(); // すべての子供を描画
popMatrix();
}
// すべての子供を描画
private void updateChildren() {
if (mChildren != null) {
for (Billboard child : mChildren) {
child.update();
}
}
}
}
OrbitalObject.pde の全コードを展開
// 円軌道を公転する天体
public class OrbitalObject extends CelestialObject {
private float mRadius; // 公転半径
private int mPeriod; // 公転周期(ミリ秒)
private float mStart; // 開始時点の角度(radians)
// コンストラクタ
// param parent 公転体の母星
// param imageName 画像のファイル名
// param w 公転体(ビルボード)の幅
// param radius 公転半径
// param period 公転周期(秒)
public OrbitalObject(CelestialObject parent,
String imageName, int w,
float radius, int period) {
super(imageName, w, 0, 0, 0);
mRadius = radius;
mPeriod = period * 1000;
mStart = random(TWO_PI);
parent.addChild(this); // 母星に自分を追加
}
// 座標変換して描画(オーバーライド)
public void update() {
updateOrbit();
super.update();
}
// 座標変換(オーバーライド)
protected void transform() {
int ms = millis();
float rd = mStart + TWO_PI * (ms % mPeriod) / mPeriod;
rotateY(rd);
translate(mRadius, 0, 0);
}
// 軌道を描画
protected void updateOrbit() {
pushMatrix();
rotateX(HALF_PI);
pushStyle();
noFill();
stroke(48, 48, 48);
strokeWeight(1);
circle(0, 0, mRadius*2);
popStyle();
popMatrix();
}
}
Galaxy.pde の全コードを展開
// 銀河を構成する星々
public class Galaxy {
private Billboard[] mStars = new Billboard[1000]; // 星の数だけのビルボード
// コンストラクタ
public Galaxy() {
// 画像配列の初期化
PImage[] images = new PImage[] {
loadImage("BlueStar50.png"),
loadImage("WhiteStar50.png"),
loadImage("YellowStar50.png"),
loadImage("OrangeStar50.png"),
loadImage("RedStar50.png"),
};
// 星の数だけループ
for (int i = 0; i < mStars.length; i++) {
float angle = random(TWO_PI); // ZX平面上の角度は0~360°(2π)の範囲でランダムに
float radius = random(4000, 5000); // ZX平面上の原点からの距離は4000~5000の範囲でランダムに
float x = sin(angle) * radius; // 星のX座標
float z = cos(angle) * radius; // 星のZ座標
float y = random(-3000, 3000); // 星のY座標は-3000~3000の範囲でランダムに
int n = (int)random(5); // ビルボードに貼り付ける画像は5種類からランダムに
mStars[i] = new Billboard(images[n], 50, x, y, z); // ビルボードを生成して配列に格納
}
}
// すべての星を座標変換して描画する
public void update() {
for (Billboard star: mStars) {
star.update();
}
}
}
SolarSystem.pde の全コードを展開
// 太陽系クラス
public class SolarSystem {
private CelestialObject mSun; // 太陽
// コンストラクタ
public SolarSystem() {
mSun = new CelestialObject("Sun.png", 50, 0, 0, 0);
OrbitalObject mercury = new OrbitalObject(mSun, "Mercury.png", 19, 227, 14);
OrbitalObject venus = new OrbitalObject(mSun, "Venus.png", 47, 425, 37);
OrbitalObject earth = new OrbitalObject(mSun, "Earth.png", 50, 587, 60);
/* moon */new OrbitalObject(earth, "Moon.png", 13, 130, 4);
OrbitalObject mars = new OrbitalObject(mSun, "Mars.png", 26, 894, 112);
OrbitalObject jupiter = new OrbitalObject(mSun, "Jupiter.png",100,1527, 711);
/* io */new OrbitalObject(jupiter, "Io.png", 14, 165, 1);
/* europa */new OrbitalObject(jupiter, "Europa.png", 12, 263, 2);
/* ganymede */new OrbitalObject(jupiter, "Ganymede.png",21, 420, 3);
/* callisto */new OrbitalObject(jupiter, "Callisto.png",19, 590, 4);
OrbitalObject saturn = new OrbitalObject(mSun, "Saturn.png", 100,2800, 886);
/* titan */new OrbitalObject(saturn, "Titan.png", 20, 479, 3);
OrbitalObject uranus = new OrbitalObject(mSun, "Uranus.png", 50,3755,1685);
OrbitalObject neptune = new OrbitalObject(mSun, "Neptune.png", 50,4410,2472);
/* triton */new OrbitalObject(neptune, "Triton.png", 11, 139, -1);
OrbitalObject pluto = new OrbitalObject(mSun, "Pluto.png", 9,5789,3716);
OrbitalObject eris = new OrbitalObject(mSun, "Eris.png", 9,6632,5580);
}
// すべての星を座標変換して描画
public void update() {
mSun.update();
}
}
CameraController.pde の全コードを展開
// カメラ制御クラス
public class CameraController {
private float mRadius = 1000; // 現在のカメラの軌道半径(ZX平面と平行な面)
private float mAngle = 0; // 現在のカメラの水平位置(軌道平面上の角度:deg)
private float mYCoord = 0; // 現在のカメラの垂直位置(Y座標:px)
private int mRadiusSpeed = 0; // カメラから見た前後方向の速度(mRadiusの変化量: px/sec)
private int mRotationalSpeed = 0; // カメラから見た左右方向の速度(mAngle の変化量:deg/sec)
private int mVerticalSpeed = 0; // カメラから見た上下方向の速度(mYCoordの変化量: px/sec)
private int mPrevMillis = 0; // 前回の経過時間
// カメラの回転速度を下げる
// カメラ視点で見た場合、
// 右へ移動中なら、右方向への変化量を下げ、
// 左へ移動中なら、左方向への変化量を上げる
public void left() {
mRotationalSpeed -= 5;
printStatus();
}
// カメラの回転速度を上げる
// カメラ視点で見た場合、
// 右へ移動中なら、右方向への変化量を上げ、
// 左へ移動中なら、左方向への変化量を下げる
public void right() {
mRotationalSpeed += 5;
printStatus();
}
// カメラの上昇速度を上げる
// カメラ視点で見た場合、
// 上昇中なら、上昇速度を上げ、
// 下降中なら、下降速度を下げる
public void up() {
mVerticalSpeed -= 25;
printStatus();
}
// カメラの上昇速度を下げる
// カメラ視点で見た場合、
// 上昇中なら、上昇速度を下げ、
// 下降中なら、下降速度を上げる
public void down() {
mVerticalSpeed +=25;
printStatus();
}
// カメラの軌道半径の変化量を下げる
// カメラ視点で見た場合、
// 前進中なら、前進速度を上げ、
// 後退中なら、後退速度を下げる
public void forward() {
mRadiusSpeed -= 10;
printStatus();
}
// カメラの軌道半径の変化量を上げる
// カメラ視点で見た場合、
// 前進中なら、前進速度を下げ、
// 後退中なら、後退速度を上げる
public void backward() {
mRadiusSpeed += 10;
printStatus();
}
// カメラの現在の状態をコンソールへ出力する
public void printStatus() {
print("(R,A,V)=(");
print((int)mRadius + "px, " + (int)mAngle + "deg, " + (int)mYCoord + "px");
print(") (dR,dA,dV)=(");
print(mRadiusSpeed + "px/s, " + mRotationalSpeed + "deg/s, " + mVerticalSpeed + "px/s");
println(")");
}
// カメラの位置を更新する
public void update() {
int ms = millis();
if (ms/1000 != mPrevMillis/1000) printStatus(); // 1秒ごとにステータス表示
int dt = ms - mPrevMillis; // 時刻の変化量
mPrevMillis = ms; // 現在時刻を退避
// 軌道半径の更新
mRadius += mRadiusSpeed * dt / 1000.0;
mRadius = max(mRadius, 100.0); // 太陽にぶつかりそうになったら止める
if (mRadius==100.0) mRadiusSpeed = 0;
// 回転角の更新
mAngle += mRotationalSpeed * dt / 1000.0;
mAngle = mAngle % 360; // 0~360に収まるように正規化
if (mAngle < 0) mAngle += 360;
// 垂直位置の更新
mYCoord += mVerticalSpeed * dt / 1000.0;
float z = mRadius * cos(radians(mAngle));
float x = mRadius * sin(radians(mAngle));
float y = mYCoord;
camera(x, y, z, 0, 0, 0, 0, 1, 0);
}
}
午前 7 時|エピローグ
惑星コルサント・共和騎士テンプル屋上にて …
若きナイト「いよいよ、軍の創設ですね」
グランド・マスター「ああ、いよいよじゃな」
若きナイト「私は昨夜の元老院議会で」
若きナイト「最高議長が行政特権を得たことが気になっています」
グランド・マスター「共和国市民の彼への支持は厚いからのぉ …」
グランド・マスター「これもまた民主主義というものじゃ」
若きナイト「実は昨夜、最高議長室から、、」
若きナイト「D.S.マークの Gopher君が出てくるところを」
若きナイト「見てしまったんです」
グランド・マスター「なに?!」
若きナイト「グランド・マスター!」
若きナイト「D.S. というのは、、」
若きナイト「ダーク・サイドの略ではないでしょうか!?」
グランド・マスター「…」
グランド・マスター「それはないじゃろう …」
グランド・マスター「もし仮に、」
グランド・マスター「彼が何らかの野心を持っていたとしても、」
グランド・マスター「誰でも気づいてしまうような」
グランド・マスター「そんなヘマはせんじゃろ …」
若きナイト「マスター …」
若きナイト「戦争になると思われますか?」
グランド・マスター「うむ、」
グランド・マスター「未来を読むのは …」
グランド・マスター「難しい …」
そう言いながら彼が目をやったとき、朝陽に照らされた巨大都市のビル群は、その煌めきを一層増していた。
あとがき
いかがでしたか?
はじめて CG プログラミングを経験した方も、意外に簡単だったと感じてもらえたのではないでしょうか。
ちょっと物足りないと思った方は、次のような改良をしてみるのも良いかもしれません。
太陽系時計
太陽を「時」、地球を「分」、月を「秒」に見立てた時計です。

次のようなことを行うことで、このような表現ができるようになります。
・ビルボードにテキストを書き込む
・ブレンディング・モードを「加算合成」にする
・太陽、地球、月が常に画角に入るようにカメラを制御する
探査機シミュレーター
探査機シミュレーター風ゲームです。
次のようなことを行うことで、このような表現ができるようになります。
・カメラを更に自由に制御する
・コントロールパネルに見立てたビルボードを常にカメラの正面に置く
ビルボードという手法は時代遅れかもしれませんが、アイデア次第では、まだまだ面白いものを作ることができそうです。
また、ちょっとだけ高校数学が必要ですが、お子さんがいらっしゃる方で、まだ夏休みの自由研究テーマが決まっていないのであれば、題材として提案してみるのも楽しそうです。
あ、画像素材などのライセンスにはくれぐれも注意してくださいね。
それでは
May the Force be with you!
(フォースと共にあらんことを!)
エンドロール後の とあるシーン
惑星コルサント 銀河共和国 最高議長室にて …
最高議長「ぐぁっはっはぁ~っ!」
最高議長「市民とは、、」
最高議長「愚かな者よのう …」
最高議長「いとも簡単に権限を引き渡しおったわ!」
最高議長「共和騎士どもも、」
最高議長「D.S. はダーク・サイドのことだと勘違いしているようだ」
最高議長「惑星系シミュレーターも手に入ったことであるし …」
最高議長「この銀河を掌握するために」
最高議長「たとえ何十年かかったとしても、、」
最高議長「私はこの D.S. を作り上げるぞ!」

この画像のビルボード素材として利用した画面中央の人口天体は adnylangager さんの作品であり、CC BY-NC 2.0 のライセンスが付与されています。
(出典: fiickr)