運営がサクラを使った場合・悪意ある参加者による妨害があった場合にも公平な抽選を可能にする面白いプロトコルを見つけましたので、ここに示します。
4行でまとめると
- 抽選を行う際に、運営がサクラを使って、実際の参加者が当選する確率を下げる可能性があります。
- 運営がサクラを使っていても、公平になる抽選のプロトコルを、コミットメントを使用することで簡単に構成できます。
- 悪意ある参加者がいた場合、適切な通信を行わず、抽選全体を妨害しえます。しかし、簡単なプロトコルでこの妨害への単純な対応をしてしまうと、運営の不正を許してしまいます。
- 悪意ある参加者がいた場合にも適切に動作するプロトコルを示します。
背景
通信プロトコルの技術を使用した、検証可能な公平なガチャの研究が行われており、先稿の「公平なガチャの私考と、コミットメントを用いた、確率に範囲を持たせることでより射幸心を煽る公平なガチャ」ではそこに用いられている技術とプロトコルの拡張を紹介しました。
さて、ガチャはユーザと運営の2人だけが参加するゲームでしたが、宝くじなどのように、多人数が参加するゲームに拡張するにはどうすればいいでしょうか?
簡単のため、N人が参加し、運営がN人の中から1人を選ぶ抽選を考えてみましょう。疑似的な方式としては、運営がN人の各人と公平なガチャのプロトコルで$\frac{1}{N}$の確率で当たりとするという方法が考えられますが、Nが大きい時、およそ$\frac{1}{e}$の確率で全く当たりが出ず、およそ$1-\frac{1}{e}-\frac{1}{eN}$の確率で当たりが2人以上に出てしまいます。当たりの景品が世界に一つしかないものだとすれば、困ったことが起きてしまうでしょう。
あるいは、N人を(先着順などで)順序付けし、実物のくじ引きのように、各人の順序通りに1人目が$\frac{1}{N}$、2人目が$\frac{1}{N-1}$、3人目が$\frac{1}{N-2}$の確率で当たるようにするという方式も考えられます。しかし、もし参加者の中に運営がサクラ(偽客)を参加させることができた場合、運営はそのサクラに秘密の情報を与えることで、不正をすることができるようになります。
本稿では、「運営がサクラを複数動員できる状態」、最悪の場合は「参加者が1人だけで、残り全員が参加者から金を巻き上げようとしている運営のサクラという状態」でも、運営が不正を行えない(サクラ耐性)プロトコルを考えます。
先行研究
暗号プロトコル技術による公平な抽選の先行研究には以下のようなものが挙げられます。
電子抽選
- D. Eastlake (2000) RFC 2777: Publicly Verifiable Nomcom Random Selection
- AgusFanarSyukri et al. (2004) ハッシュ関数を用いた公平な電子抽選方法
- 乱数発生は外部機関による
- Chin-Ling Chen et al. (2014) A Secure and Fair Joint E-Lottery Protocol
- ハッシュ値で乱数を生成
- Nasrollah Pakniat and Ziba Eslami (2011) A Proxy E-Raffle Protocol Based on Proxy Signatures
以下の先行研究はネット上にないため検証できていません。
- 佐古 和恵 (1998) 公平性保証メカニズム--電子抽選,電子投票 (セキュリティ特集) -- (基盤技術)
- 佐古 和恵 (2000) 2.事例 公平性保証とプライバシー保護
- Chun-I Fan et al. (2009) Anonymous Electronic Lottery Protocol
- 山本 雅晴、真鍋 義文 (2016) 仲介人を用いた仮想通貨のための宝くじプロトコル
ブロックチェーンを使用したもの
- Ethereumで賭博場ルールを考えてみた
- ブロックチェーンとスマートコントラクトで、抽選の公正性を証明する
- 以下の記事には、ブロックチェーンで検証可能な乱数を生成する議論へのリンクがあります。
最近はブロックチェーンを用いたプロトコルや、量子コンピュータを用いた研究の方が隆盛のようですが、ここではもっとシンプルに、コミットメントという古典的手法を用いたプロトコルを考えます。個人的には、ブロックチェーンに運営や参加者が介入可能な状態では、単に予測の難しい値を当選者を選ぶのに使用するのは危険1な気がするのですが、どうなのでしょうか?
要素技術
詳細に関しては、先稿の要素技術の章もご参照下さい。
電子署名
RSA公開鍵暗号方式やDSA署名などで実現される電子署名です。通信の否認防止に使用できます。情報の送信時に、今までの通信履歴(のハッシュ値)を付けて電子署名付きで送信することで、今までの通信の否認防止が実現でき、一つのプロトコルの中で一貫性を持たせることができます。
コミットメント
「コミット」と「公開」の2つのフェーズから構成される通信で、送信者は、送信したい値$m$を暗号化、$C$として「コミット」のフェーズで送信し、その後送信したい値$m$と検証用のデータ$v$を「公開」フェーズで送信します。受信者は「公開」フェーズで受信したデータ$m$, $v$を使用して値が正しいか検証します。コミットメントの方式によっては、最初にコミットを生成するための値の受け渡しをする「前準備」フェーズを持つ場合があります。
送信者は一度「コミット」した後に「公開」のフェーズで送信したい値$m$を改ざんすることはできず(拘束性)、受信者は「コミット」された段階では送信したい値$m$を知ることはできません(秘匿性)。
常に拘束性が成立するコミットメントを「完全拘束」、計算量的に困難である場合を「計算量拘束」、同様に常に秘匿性が成立するものを「完全秘匿」、計算量によるものを「計算量秘匿」といいます。
完全拘束で完全秘匿なコミットメントは存在しませんが、完全拘束・計算量秘匿なコミットメントか、完全秘匿・計算量拘束なコミットメントが構成可能です。
コミットメントの転送
以下のような、AliceがBobに送ったコミットメントを、BobがCharlieに転送するという通信を考えます。
- (前準備が必要な場合)BobがAliceに前準備の通信を行う
- AliceがBobに値$m$のコミットメントのコミット$C$を送信
- BobがCharlieに、Aliceのコミットメントと称して$C$を転送
- AliceがBobにコミットメントの公開として値$m$と検証用データ$v$を送信、Bobが検証
- BobがCharlieに、Aliceのコミットメントの公開と称して値$m$と検証用データ$v$を転送、Charlieが検証
このような通信においては、当然、ステップ3とステップ5において、BobがCharlieに偽物の値を転送することが考えられます。
ここで、BobがCharlieに送信したコミットメントが、BobとCharlieの間のコミットメントとみなせるかどうかを考えます。
前準備が必要なコミットメントの方式で、秘匿性や拘束性が前準備に依存しているような方式では、BobとCharlieの間で前準備を行っていないため、秘匿性や拘束性を満たせないと言えます。
逆に、前準備が不要なコミットメントの場合、BobとCharlieの間の通信は通常のコミットメントと同様であるため、BobとCharlieの間のコミットメントとみなせると言えます。
先稿のコミットメントの方式では、離散対数問題を利用したコミットメントは前準備が必要なため、コミットメントとみなせませんが、公開鍵暗号方式やハッシュ値を利用したコミットメントは前準備が不要のため、コミットメントとみなせると言えます。
前準備が必要なコミットメントの方式でも、ステップ1でBobがAliceに転送を行うという名目で、ステップ1の前に、CharlieがBobに前準備の通信を行う場合は、BobとCharlieの間のコミットメントとみなせると言えます。ただし、上記の通信ではCharlieが複数でもBobによる転送が可能ですが、CharlieがBobに前準備の通信を行う場合は、Charlieが事前にわかっており、Charlieが1人の場合にしか適用できないと言えます。
総和の剰余
m人のユーザが0以上N未満の整数を乱数として生成するには、各ユーザに0以上N未満の整数を送信させ、その総和をNで割った数を乱数とするという手法がよく用いられます。Nが2の場合は、この操作は排他的論理和xorと同じ操作となります。
m人のユーザの内、少なくとも1人でも他のユーザと非協力関係にあり、そのユーザは他ユーザの送信する整数を知らず、他ユーザもそのユーザの送信する整数を知らない場合、この操作の結果は1/Nの等確率で0以上N未満の整数を一様乱数として生成できるとみなすことができます。
問題の定義
N人の参加者の中から、1人の当選者を選ぶプロトコルを考えます。
登場人物
- 運営: 抽選を主宰。すべての参加者は運営と通信を行うものとします。参加者にサクラを紛れ込ませることができ、不正ができるならば、なるべくサクラを当選者にしようとします。
-
参加者: N人の参加者。先着順などの順序で、$0$番目の参加者から$N-1$番目の参加者までと順序付けられています。
- 実際の参加者: 最低1人いるものとします。
- サクラ: この中には複数人(最大N-1人)の運営のサクラが含まれており、運営の秘匿している情報を知ることができます。
- グループ: 実際の参加者も、複数人がグループを形成し、互いに秘匿している情報を共有することが可能です(通常のくじ引きで、1人が複数口申し込む場合に相当)。
参加者に運営のサクラが含まれている前提であるため、参加者が運営を兼任することも考えられます。また、運営が、だれがサクラかを公表して、その人が当選した場合を、通常の抽選における「全員はずれ」という扱いにすることも考えられます。
実際の参加者がグループを形成できると、運営が不正をした場合に見つけられる可能性がありますが、最悪の場合の「実際の参加者が1人だけで、残り全員がサクラ」にも対応できるように、これについては考えないものとします。
信頼できる第三者
- 公開鍵基盤: 各参加者と運営の公開鍵を公開し、それが各参加者と運営の公開鍵であることを証明します。
- 司法機関: 各参加者や運営からの訴えを受け、訴えた人がその主張を証明した時、然るべき処置をします。
行いたいこと
- 各参加者は、$\frac{1}{N}$の確率で当選者になります。
満たすべき性質
- 各参加者の当選率が$\frac{1}{N}$であることを保証・検証できる
- 運営にとって、プロトコルが正しく実行された時、当選者は0人になることも、複数人になることもない
- 各参加者は、少なくとも運営と自分自身の間のプロトコルが正しく実行された時、自分の通信履歴を提示することで、プロトコルが正しく実行されたことと、自分が当選したかどうかを司法機関に証明できる
- 運営は、プロトコルが正しく実行された時、自分の通信履歴を提示することで、プロトコルが正しく実行されたことと、誰が当選したかを司法機関に証明できる
- 各参加者は、少なくとも運営と自分自身の間のプロトコルが正しく実行されなかったとき、自分の通信履歴を提示することで、正しく実行されなかったことを司法機関に証明できる
- 運営は、プロトコルが正しく実行されなかったとき、自分の通信履歴を提示することで、正しく実行されなかったことを司法機関に証明できる
- プロトコルが途中で中断された場合は、各参加者は、司法機関の立会いの下、運営に対してプロトコルを継続させるものとする
簡単な抽選のプロトコル
このような公平な抽選のプロトコルとして、以下のようなプロトコルを誰でも簡単に思いつくと思います。
以下のプロトコルの通信は、今までの通信履歴(のハッシュ値)を付けて電子署名付きで送信が行われるものとします。また、コミットメントには前準備不要のコミットメントを使用するものとします(複数人に転送するため)。
- 運営は、
- 0以上N未満の整数mをランダムに生成し、
- mのコミットメントのコミットの情報を全参加者に送信する
- 全参加者は(参加者の番号を$k$として)、
- 0以上N未満の整数$n_k$をランダムに生成し、
- $n_k$のコミットメントのコミットの情報を運営に送信する
- 運営は、全参加者から受信した$n_k$のコミットメントを、その参加者以外の全参加者に転送する
- 全参加者は、運営に$n_k$のコミットメントの公開を送信する
- 運営は、
- 全参加者から受信した$n_k$の公開を、その参加者以外の全参加者に転送し、
- mのコミットメントの公開を全参加者に転送し、
- $m$と各$n_k$の総和の剰余($(m + \sum_{k=0}^{N-1} n_k) \bmod{N}$)に対応する参加者を当選とする
- 全参加者は、運営から受信したコミットメントの公開を検証し、自分が当選したかどうかを検証する
簡単な抽選のプロトコルの性質
ステップ1で運営が$m$のコミットメントを送信しましたが、全参加者がグループを形成している場合に、誰が当選するかを調整できてしまう問題に対処するために送信しているため、そのような問題の対処が不要な場合は省略が可能です。
ステップ3・ステップ5で、運営は全参加者にコミットメントを転送していますが、参加者にとってはこの際に運営が本当に他参加者のコミットメントを送信していなくても問題ありません。前準備不要のコミットメントを使用しているため、自分が運営に送信した$n_k$がコミットの段階では運営に分からず、運営が自分に送信したコミットメントの値を変更できなければ、ステップ5で自分が当選する確率は$\frac{1}{N}$になるためです。
ステップ3と5で運営が全参加者にコミットメントを転送していますが、上記の理由により個別には参加者と運営のやり取りとみなせるため、誰のコミットメントかは公表する必要はありません。公表しないことにより、参加者の番号をランダムにするなどの方法で、参加者同士では誰が当選したかを知らないという匿名性を実現することができます。
しかし、この簡単な抽選のプロトコルには、悪意ある参加者がいた場合、以下のような問題が発生する可能性があります。
簡単な抽選のプロトコルの問題点
妨害攻撃
公平なガチャのプロトコルでは、運営が通信を中止しない限りは、ユーザが途中で通信を放棄してもユーザ自身が損をするか、通信が無駄になったという損失だけで済みました。しかし抽選では、参加者の内誰か1人でも通信を放棄してしまうと、他の参加者全員に迷惑が掛かってしまいます。
よって、運営のライバル会社などが、抽選を妨害してやろうと思って参加者を送り込み、コミットメントの公開の通信を行わないなどの妨害を行うと、その抽選がダメになってしまいます。そのような抽選を妨害する攻撃を、ここでは妨害攻撃と呼ぶこととします。
妨害攻撃を逆手に取った運営による不正
このような妨害攻撃に対して、「制限時間を設けて、時間内にコミットメントを公開しなかった参加者は無視すればいいじゃないか・その参加者を除外して抽選をやり直せばいいじゃないか」と思う方も少なくないかもしれません。しかし、このような単純な対応だと、運営の不正を許してしまうことになります。
妨害攻撃にあったら抽選をやり直す場合
制限時間内にコミットメントを公開しない参加者がいた場合、その参加者を除外して抽選をやり直す場合を考えます。
この場合、運営はサクラ以外の全参加者の公開が済んだ段階で誰が当選したかが分かりますので、サクラが当選しなかった場合にサクラの内誰かを制限時間超えさせることで、抽選をやり直させることができてしまい、結果として実際の参加者が当選する確率が下がってしまいます。
妨害攻撃にあったら無視する場合
制限時間内にコミットメントを公開しない参加者がいた場合、その参加者のコミットメントを無視する場合を考えます。
この場合、運営は$N/2$人のサクラを用意し、実際の参加者とサクラが交互になるように番号を調整し、サクラ全員に1をコミットさせます。運営はサクラ以外の全参加者の公開が済んだ段階で誰が当選したかが分かりますので、サクラが当選しなかった場合に、サクラの内誰かを制限時間超えさせることで、当選者の番号を1ずらし、サクラを当選させます。
問題の再定義
妨害攻撃がある前提で、問題の再定義を行います。
N人の参加者の中から、1人の当選者を選ぶプロトコルを考えます。
登場人物
- 運営: 抽選を主宰。すべての参加者は運営と通信を行うものとします。参加者にサクラを紛れ込ませることができ、不正ができるならば、なるべくサクラを当選者にしようとします。
-
参加者: N人の参加者。先着順などの順序で、$0$番目の参加者から$N-1$番目の参加者までと順序付けられています。
- 実際の参加者: 最低1人いるものとします。
- サクラ: この中には複数人(最大N-1人)の運営のサクラが含まれており、運営の秘匿している情報を知ることができます。妨害攻撃者のふりをすることもできます。
- グループ: 実際の参加者も、複数人がグループを形成し、互いに秘匿している情報を共有することが可能です(通常のくじ引きで、1人が複数口申し込む場合に相当)。
- 妨害攻撃者: 制限時間内にするべき通信をしないなどの方法で抽選を妨害します。最大N-1人です。
信頼できる第三者
- 公開鍵基盤: 各参加者と運営の公開鍵を公開し、それが各参加者と運営の公開鍵であることを証明します。
- 司法機関: 各参加者や運営からの訴えを受け、訴えた人がその主張を証明した時、然るべき処置をします。
- タイムスタンプ証明機関: かなり強い仮定ですが、参加者・運営が制限時間内に通信を行ったことを証明します。
制限時間内に通信をしたという証明のために、タイムスタンプ証明機関というかなり強い仮定をしましたが、信頼できる機関が配達証明のようなものを行っていると想定してください。実現方法に関する議論はあるとは思いますが、本稿ではこれ以上は立ち入らないものとします。
行いたいこと
- 実際の参加者は、最低$\frac{1}{N}$の確率で当選者になります
- すべての通信には制限時間がついています
- 運営は必ず制限時間内に通信を行うものとします(制限時間内に行わなかった場合は参加者が司法機関に訴えるものとします)
- 妨害攻撃者が通信を行わなかった場合、妨害攻撃者は当選しないものとします
- 妨害攻撃者が当選しなくなったことで、実際の参加者の当選率が均等に上がる必要はないものとします
満たすべき性質
- 各参加者の当選率が$\frac{1}{N}$であることを保証・検証できる
- 運営にとって、プロトコルが正しく実行された時、当選者は0人になることも、複数人になることもない
- 各参加者は、少なくとも運営と自分自身の間のプロトコルが正しく実行された時、自分の通信履歴を提示することで、プロトコルが正しく実行されたことと、自分が当選したかどうかを司法機関に証明できる
- 運営は、プロトコルが正しく実行された時、自分の通信履歴を提示することで、プロトコルが正しく実行されたことと、誰が当選したかを司法機関に証明できる
- 各参加者は、少なくとも運営と自分自身の間のプロトコルが正しく実行されなかったとき、自分の通信履歴を提示することで、正しく実行されなかったことを司法機関に証明できる
- 運営は、プロトコルが正しく実行されなかったとき、自分の通信履歴を提示することで、正しく実行されなかったことを司法機関に証明できる
- 妨害攻撃者が制限時間内に通信を行わなくても、プロトコルが実行可能で、実際の参加者の当選率が保証される
妨害攻撃耐性のある抽選プロトコルの概念
妨害攻撃耐性を考える際は、参加者がコミットメントを公開した後のタイミングなどで、運営が他参加者が正しく通信を行っても正しく通信を行わなかったと偽る、あるいはサクラにわざと制限時間超えをさせうるということに注意します。
まずは、中心となる考えを示すために、概念的なプロトコルを示します。
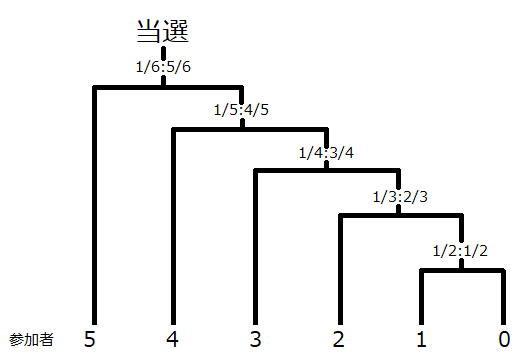
確率付きトーナメント
以下の性質を利用したトーナメントを考えます。
\frac{1}{2}\frac{2}{3}\frac{3}{4}\dots\frac{(N-2)}{(N-1)}\frac{(N-1)}{N} = \frac{1}{N}
0番目の参加者と、1番目の参加者が$\frac{1}{2}$と$\frac{1}{2}$の確率で勝つコイントスを行い、続いてその勝者と2番目の参加者が$\frac{2}{3}$と$\frac{1}{3}$の確率で勝つコイントスを行い(2番目の参加者の勝率が$\frac{1}{3}$)、さらにその勝者と3番目の参加者が$\frac{3}{4}$と$\frac{1}{4}$の確率で勝つコイントスを行います。これを、今までの勝者と$N-1$番目の参加者が$\frac{N-1}{N}$と$\frac{1}{N}$の確率で勝つコイントスを行うまで繰り返し、最後の勝者を当選者とします。このようなトーナメントを行うと、全ての参加者の当選率は、上記の等式により、全て$\frac{1}{N}$となります。
もしこのトーナメントの参加者に妨害攻撃者がいて、コイントスで適切な通信を行わなかった場合は不戦敗とします。これにより、実際の参加者は、運良く相手が不戦勝になって自分の当選率が上がることがあっても、当選率が$\frac{1}{N}$以上になることは保証されます。
妨害攻撃耐性のある抽選プロトコルのベース
以下のプロトコルの通信は、今までの通信履歴(のハッシュ値)を付けて電子署名付きで送信が行われるものとします。全ての通信には制限時間がついており、タイムスタンプ証明機関が制限時間内に通信を行ったことを証明するものとします。コミットメントの転送は1人に対して行うため、前準備が必要なコミットメントでも可です。
- 以下のコイントスを、$i=1$から$i=N-1$まで繰り返す。繰り返し中の「勝者」の初期値は、0番目の参加者とする
- 勝者は、0以上$i+1$未満の整数$n$をランダムに生成し、$n$のコミットメントのコミットを運営に送信する
- i番目の参加者は、0以上$i+1$未満の整数$m$をランダムに生成し、$m$のコミットメントのコミットを運営に送信する
- 運営は、$m$のコミットメントのコミットを勝者に転送する
- 運営は、$n$のコミットメントのコミットをi番目の参加者に転送する
- 勝者は、$n$のコミットメントの公開を運営に送信する
- i番目の参加者は、$m$のコミットメントの公開を運営に送信する
- 運営は、$m$のコミットメントの公開を勝者に転送する
- 運営は、$n$のコミットメントの公開をi番目の参加者に転送する
- $n$と$m$の総和の剰余 $(n+m) \bmod{i+1}$ が0の時、i番目の参加者を次の繰り返しの勝者とし、0以外の場合は現在の勝者を次の繰り返しの勝者とする
- 上記の繰り返しが終了したときの勝者を当選者とする
ステップ1の繰り返しで、参加者が制限時間内に正しい値を送信しない場合は対戦相手の不戦勝、2人とも送信しない場合は次の繰り返しの参加者を不戦勝とします。
各回のコイントスでは、参加者は本質的に運営とコイントスを行うのと同様の通信になります。このため、参加者は相手の参加者が誰かを知る必要はなく、匿名性をより高めることができます。
ステップ1-9では、総和の剰余の代わりに、$n=m$かどうかで判定することが可能です。
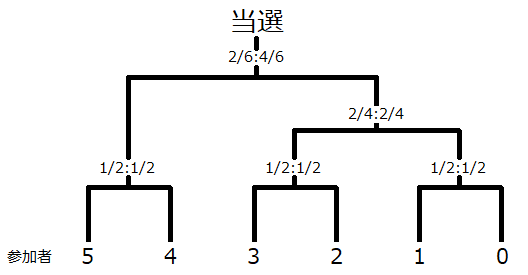
さらに、ここでは簡単のために線形のトーナメントで記述しましたが、その結果0番目の参加者が当選するにはN回の通信が必要になりました。通常のトーナメントのように二分させることで、この通信を$\log_2(N)$回に抑えることができるようになります。
妨害攻撃耐性のある抽選プロトコル
上記のプロトコルのコイントスの通信を工夫することで、幾通りかのプロトコルを書くことができます。
簡易化したコイントスを逐次行うプロトコル
以下のプロトコルの通信は、今までの通信履歴(のハッシュ値)を付けて電子署名付きで送信が行われるものとします。全ての通信には制限時間がついており、タイムスタンプ証明機関が制限時間内に通信を行ったことを証明するものとします。コミットメントの転送は1人に対して行うため、前準備が必要なコミットメントでも可です。
- 以下を、初期値$U=0$として、$i=1$から$i=N-1$まで繰り返す。
- U番目の参加者(勝者)は、0以上$i+1$未満の整数$n$をランダムに生成し、$n$のコミットメントのコミットを運営に送信する
- 運営は、$n$のコミットメントのコミットをi番目の参加者に転送する
- i番目の参加者は、0以上$i+1$未満の整数$m$をランダムに生成し、$m$を運営に送信する
- 運営は、$m$をU番目の参加者に転送する
- U番目の参加者は、$n$のコミットメントの公開を運営に送信する
- 運営は、$n$のコミットメントの公開をi番目の参加者に転送する
- $n$と$m$の総和の剰余 $(n+m) \bmod{i+1}$ が0の時、次の繰り返しの$U$を$i$とし、0以外の場合は現在の$U$とする
- 上記の繰り返しが終了したとき、U番目の参加者を当選者とする
ステップ1の繰り返し中で、U番目の参加者が正しい通信を制限時間に行わなかった場合はその回の繰り返しを終了し、次の繰り返しの$U$を$i$、i番目の参加者が行わなかった場合は次の繰り返しの$U$を現在の$U$とします。
コミットをすべて先に送信するプロトコル
以下のプロトコルの通信は、今までの通信履歴(のハッシュ値)を付けて電子署名付きで送信が行われるものとします。全ての通信には制限時間がついており、タイムスタンプ証明機関が制限時間内に通信を行ったことを証明するものとします。コミットメントの転送先が事前にわからないため、前準備不要なコミットメントを使用するものとします。
- 全参加者は、参加者の番号を$k$として、以下の配列$A_k$をランダムに生成し、$A_k$の各要素をそれぞれコミットメントに入れ、それらのコミットを運営に送信する
- $A_k$の添字はkから$N-1$
- 添字$i(k < i < N)$に対して、$A_k[i]$は0以上$i+1$未満のランダムな整数
- 以下を、初期値$U=0$として、$i=1$から$i=N-1$まで繰り返す。
- 運営は、$A_U[i]$のコミットメントのコミットをi番目の参加者に転送する
- 運営は、$A_i[i]$のコミットメントのコミットをU番目の参加者に転送する
- i番目の参加者は$A_i[i]$のコミットメントの公開を運営に送信する
- U番目の参加者は$A_U[i]$のコミットメントの公開を運営に送信する
- 運営は、$A_i[i]$のコミットメントの公開をU番目の参加者に転送する
- 運営は、$A_U[i]$のコミットメントの公開をi番目の参加者に転送する
- $A_U[i]$と$A_i[i]$の総和の剰余 $(A_U[i]+A_i[i]) \bmod{i+1}$ が0の時、次の繰り返しの$U$を$i$とし、0以外の場合は現在の$U$とする
- 上記の繰り返しが終了したとき、U番目の参加者を当選者とする
ステップ1の繰り返し中で、U番目の参加者が正しい通信を制限時間に行わなかった場合はその回の繰り返しを終了し、次の繰り返しの$U$を$i$、i番目の参加者が行わなかった場合は次の繰り返しの$U$を現在の$U$とします。
参加者がコミットと公開の2回しか送信をしないプロトコル
以下のプロトコルの通信は、今までの通信履歴(のハッシュ値)を付けて電子署名付きで送信が行われるものとします。全ての通信には制限時間がついており、タイムスタンプ証明機関が制限時間内に通信を行ったことを証明するものとします。コミットメントを複数の転送先に転送するため、前準備不要なコミットメントを使用するものとします。
- 全参加者は、参加者の番号を$k$として、以下の配列$A_k$をランダムに生成し、$A_k$の各要素をそれぞれコミットメントに入れ、それらのコミットを運営に送信する
- $A_k$の添字はkから$N-1$
- 添字$i(k < i < N)$に対して、$A_k[i]$は0以上$i+1$未満のランダムな整数
- 以下を、$i=0$から$i=N-1$まで繰り返す。
- 運営は、$A_{i+1}[i+1], A_{i+2}[i+2], \dots A_{N-1}[N-1]$のコミットメントのコミットをi番目の参加者に転送する
- 0番目の参加者は、$A_0$の全てのコミットメントの公開を運営に送信する
- 以下を、初期値$U=0$として、$i=1$から$i=N-1$まで繰り返す。
- 運営は、$A_U[i]$の平文をi番目の参加者に送信する
- i番目の参加者は、$A_i[i]$の全てのコミットメントの公開を運営に送信する
- 運営は、$A_i[i]$のコミットメントの公開をU番目の参加者に転送する
- $A_U[i]$と$A_i[i]$の総和の剰余 $(A_U[i]+A_i[i]) \bmod{i+1}$ が0の時、次の繰り返しの$U$を$i$とし、0以外の場合は現在の$U$とする
- 上記の繰り返しが終了したとき、U番目の参加者を当選者とする
ステップ3で0番目の参加者が正しい通信を制限時間に行わなかった場合は、1番目の参加者が$A_1$、1番目の参加者も正しい通信を行わなかった場合は更に2番目の参加者にと通信を求めていき、最初に正しい通信を行った$l$番目の参加者に対して、$A_l$のコミットメントの公開を運営に送信し、ステップ4の繰り返しを、初期値$U=l$、iの繰り返しの範囲を$i=l+1$からとして実行します。
ステップ4の繰り返し中で、i番目の参加者が正しい通信を制限時間に行わなかった場合はその回の繰り返しを終了し、次の繰り返しの$U$を現在の$U$とします。
このプロトコルでは、参加者はステップ3もしくは4で1回のみコミットメントの公開を運営に送信します。これにより送信の回数は2回だけで済ませることができます。ただ、このプロトコルは線形のトーナメントの、対戦相手が事前に分かるという性質を使用しており、公開の送信までに最悪で$O(N)$の待ち時間が発生します。
抽選プロトコルの性質
全参加者は、直接には運営としか通信を行っていません。このため、参加者にとっては、最終的には自分の当選率が$\frac{1}{N}$以上になるようなコイントスを複数回やっているように見えます。よって、たとえ運営が不正をしていて、他の参加者のコミットメントを転送せずに運営が勝手に生成したコミットメントを送信していたとしても、自分とのコイントスさえ正しく行っていれば、自分の当選率は保証されていると言えます。
また、この理由により、参加者は自分が実際には誰とコイントスをしているのかを知る必要はなく、これにより参加者同士には誰が当選したかが分からないという匿名性を実現することができます。
正しい情報を制限時間内に送信しない参加者がいた場合には、残りの全参加者の当選率が均一に上昇するのではなく、いずれかの参加者1人だけの当選率が上昇します。しかし、実際の参加者がこれを狙おうとしても、送信しない参加者を用意するよりも、自分が複数口参加したほうが当選率が高いため、メリットが無いということになります。
まとめ
公平な抽選のプロトコルを考える際に、運営がサクラを使った場合にも対応できる簡単な公平な抽選のプロトコルを紹介しました。そして、そのプロトコルは悪意ある参加者が妨害攻撃を行いえることと、妨害攻撃への単純な対策を行うと運営の不正を許してしまうことを示しました。
最終的に、運営がサクラを使いえて、妨害攻撃にも対応できるプロトコルを、トーナメントの形で構成できることを示しました。
先行研究との比較
乱数をオラクル的に外部に依存する先行研究に比べ、本稿のプロトコルは、プロトコル自体によって抽選の当選確率を保証します。
このため、運営や参加者が乱数生成に影響を与えることを心配する必要が生じません。
先行研究では、参加者に対する要件として、参加者の通信の最小化、特に1回参加を表明するだけで正しく動作することを目指すものがありますが、本稿はコミットメントを動作の主軸にしているために、必然的に参加者に複数回の動作を要求してしまいます。
まだ先行研究を十分に読み込めていないため、機会があればまた比較を書いてみたいと思います。また、もし電子抽選プロトコルに関する先行研究をご存知の方は教えてください。
今後の課題
運営にもわからない匿名性
本稿のプロトコルでは、参加者同士には誰が当選者かが分からない匿名性を持ちましたが、運営には誰が当選したかが分かります。これをさらに、運営にも当選者がわからないという匿名性を実現することは可能でしょうか?
平等な当選率の上昇
本稿のプロトコルでは、制限時間内に正しい通信を行わなかった参加者がいても、全員の当選率が平等に上昇するわけではなく、ランダムに特定のユーザの当選率が上昇していました。これを、全員平等に当選率を上昇させることは可能でしょうか?
参加者の送信回数の削減と通信時間の削減の両立は可能か?
本稿のプロトコルでは、「コミットをすべて先に送信するプロトコル」などのトーナメントを並列化することで$O(\log_2(N))$まで通信時間を抑えることができますが、参加者の送信回数も$\log_2(N)$回必要になりました。一方「参加者がコミットと公開の2回しか送信をしないプロトコル」では、参加者の送信回数は2回になりますが、通信時間は$O(N)$かかってしまいました。参加者の送信回数の削減と通信時間の削減の両立は可能でしょうか?
-
例えば、どこかの企業の株価をもとに当選を決める場合、参加者や運営がその株を買って操作してしまうことが考えられるのではないかと思います。ブロックチェーンの特定の期日の最終ブロック番号をもとに当選を決める場合は、参加者や運営が自分の都合のいい値になるように操作できないというのはProof-of-Workで証明できるのでしょか? ↩