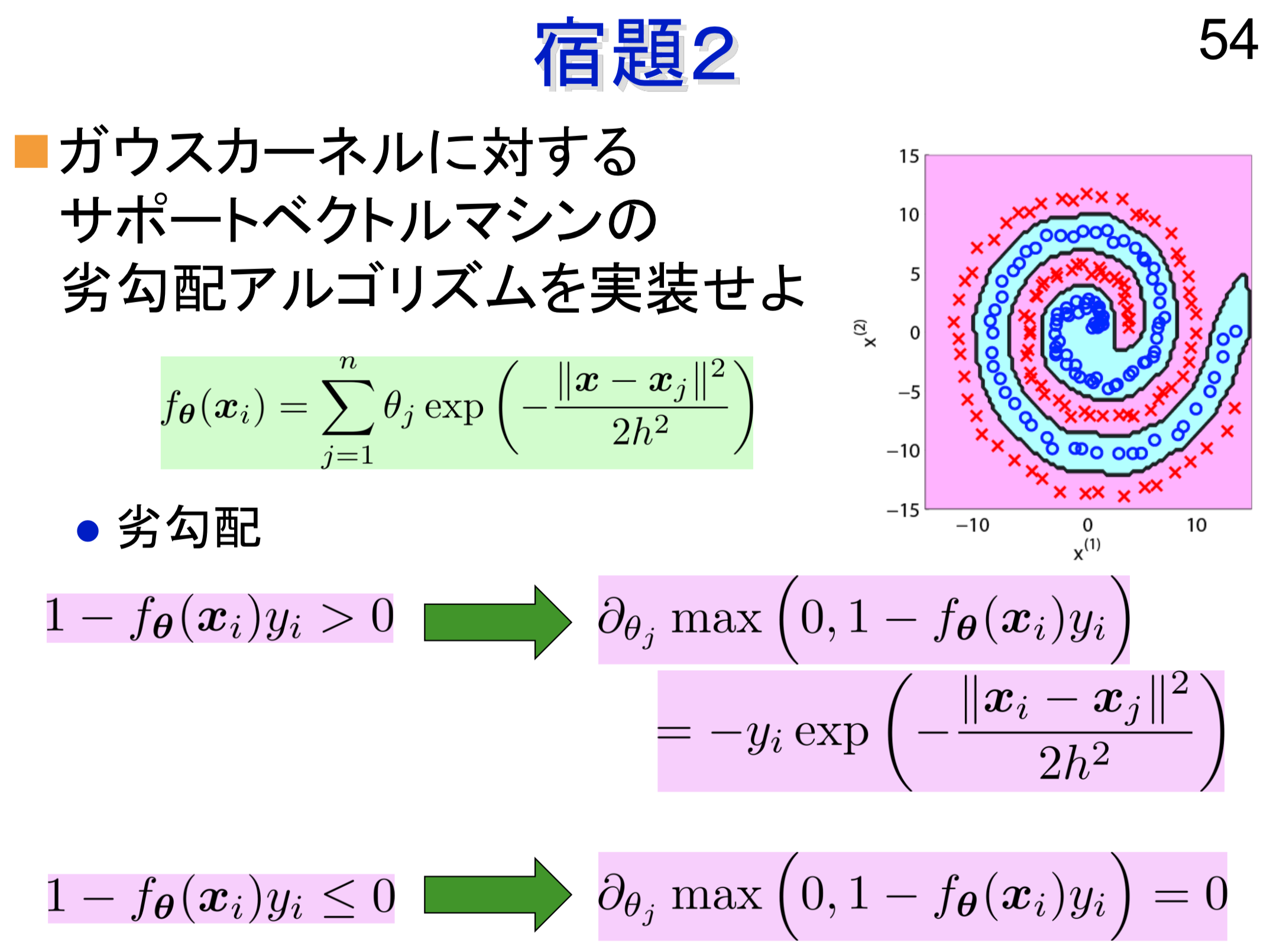
ワンライナーでSVMを書く
この記事はIS17erアドベントカレンダー11日目の記事です。
経緯
まじでネタがなかった
SVM
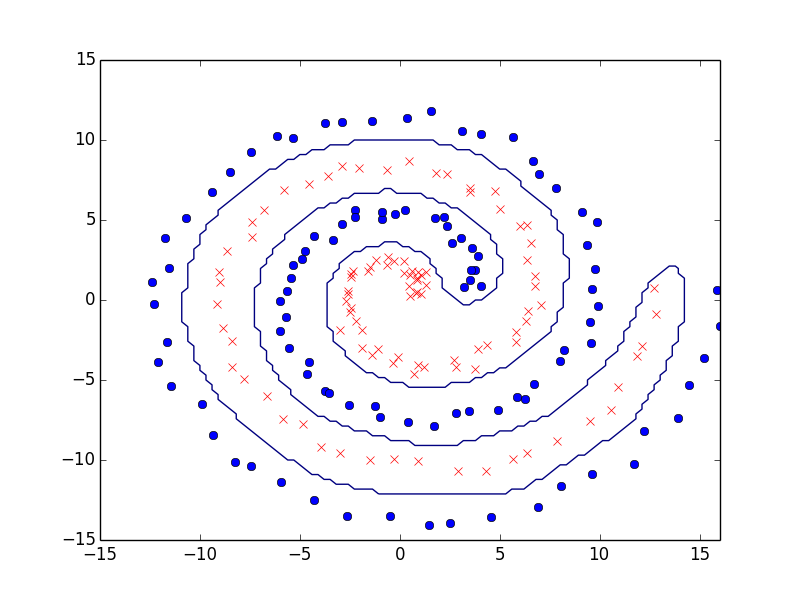
結果
svm-oneliner.py
import numpy as np; import matplotlib.pyplot as plt; kernel=lambda p,q,hh=2:np.exp(-np.linalg.norm(p-q)**2/2/hh**2); svm=lambda x,y:[globals().update({'C':1,'eps':0.1,'t':np.matrix(np.zeros(y.size)),'K':np.matrix([[kernel(x[i],x[j]) for i in range(y.size)] for j in range(y.size)])}),[(globals().update({'sd':np.zeros(y.size)}),[1-K[i].dot(t.T)*y[i]>0 and globals().update({'sd':sd-K[i]*y[i]}) for i in range(y.size)],globals().update({'t':t-eps*(C*sd+2*K.dot(t.T).T),'eps':eps*0.95})) for _ in range(100)],globals().update({'svm_ret':lambda p:-1 if t.dot(np.matrix([kernel(p,x[i]) for i in range(y.size)]).T)[0,0] < 0 else 1})]; n=100; xp=np.linspace(0,4*np.pi,n); d=lambda: np.random.uniform(0,1); x1=[[p*np.cos(p)+d(),p*np.sin(p)+d()] for p in xp]; x2=[[(p+np.pi)*np.cos(p)+d(),(p+np.pi)*np.sin(p)+d()] for p in xp]; y1=[1 for _ in range(n)]; y2=[-1 for _ in range(n)]; xs=np.array(x1+x2); ys=np.array(y1+y2); svm(xs,ys); dn=100; dh=np.linspace(-15,15,dn); mx,my=np.meshgrid(dh,dh); mz=map(lambda v:map(svm_ret,v),np.array([my,mx]).T); plt.contour(mx,my,mz,levels=[0]); fst=lambda x:x[0]; snd=lambda x:x[1]; plt.plot(map(fst,x1),map(snd,x1),'xr'); plt.plot(map(fst,x2),map(snd,x2),'ob'); plt.show()
ショートコーディングは意識していないので、比較的読みやすい(?)と思います。
元のコード
svm.py
import numpy as np
import matplotlib.pyplot as plt
hh = 2
def kernel(p, q):
d = np.linalg.norm(p - q)
return np.exp(-d ** 2 / 2 / hh ** 2)
def svm(x, y):
n = y.size
C, eps = 1, 0.1
t = np.matrix(np.zeros(n))
K = np.matrix([[kernel(x[i], x[j]) for i in range(n)] for j in range(n)])
for _ in range(100):
sd = np.zeros(n)
for i in range(n):
if 1 - K[i].dot(t.T) * y[i] > 0:
sd = sd - K[i] * y[i]
t -= eps * (C * sd + 2 * K.dot(t.T).T)
eps *= 0.95
def f(p):
a = t.dot(np.matrix([kernel(p, x[i]) for i in range(n)]).T)
return -1 if a[0, 0] < 0 else 1
return f
n = 100
xp = np.linspace(0, 4 * np.pi, n)
d = lambda: np.random.uniform(0, 1)
x1 = [[p * np.cos(p) + d(), p * np.sin(p) + d()] for p in xp]
x2 = [[(p + np.pi) * np.cos(p) + d(), (p + np.pi) * np.sin(p) + d()] for p in xp]
y1 = [1 for _ in range(n)]
y2 = [-1 for _ in range(n)]
xs = np.array(x1 + x2)
ys = np.array(y1 + y2)
f = svm(xs, ys)
dn = 100
dh = np.linspace(-15, 15, dn)
mx, my = np.meshgrid(dh, dh)
mz = map(lambda v: map(f, v), np.array([my, mx]).T)
plt.contour(mx, my, mz, levels=[0])
fst = lambda x: x[0]
snd = lambda x: x[1]
plt.plot(map(fst, x1), map(snd, x1), 'xr')
plt.plot(map(fst, x2), map(snd, x2), 'ob')
plt.show()