線形回帰分析をする時、誤差項が同じ分布に従うという条件があります。分散不均一の場合、一般線形モデル(GLM、General linear model)で分析することが知られています。分散不均一性を検出する方法は、いくつあります。今日は、例を挙げて、Breusch–Pagan検定を紹介します。
Breusch–Pagan検定は、下記URLに参考してください。ここで説明しません。
https://en.wikipedia.org/wiki/Breusch%E2%80%93Pagan_test
簡単に説明します。図Total、A、B、C、D、Eは豆腐の生産量を表しています。生産量を目的関数と、気温、気温差、降水量を説明変数とし、モデル構築します。
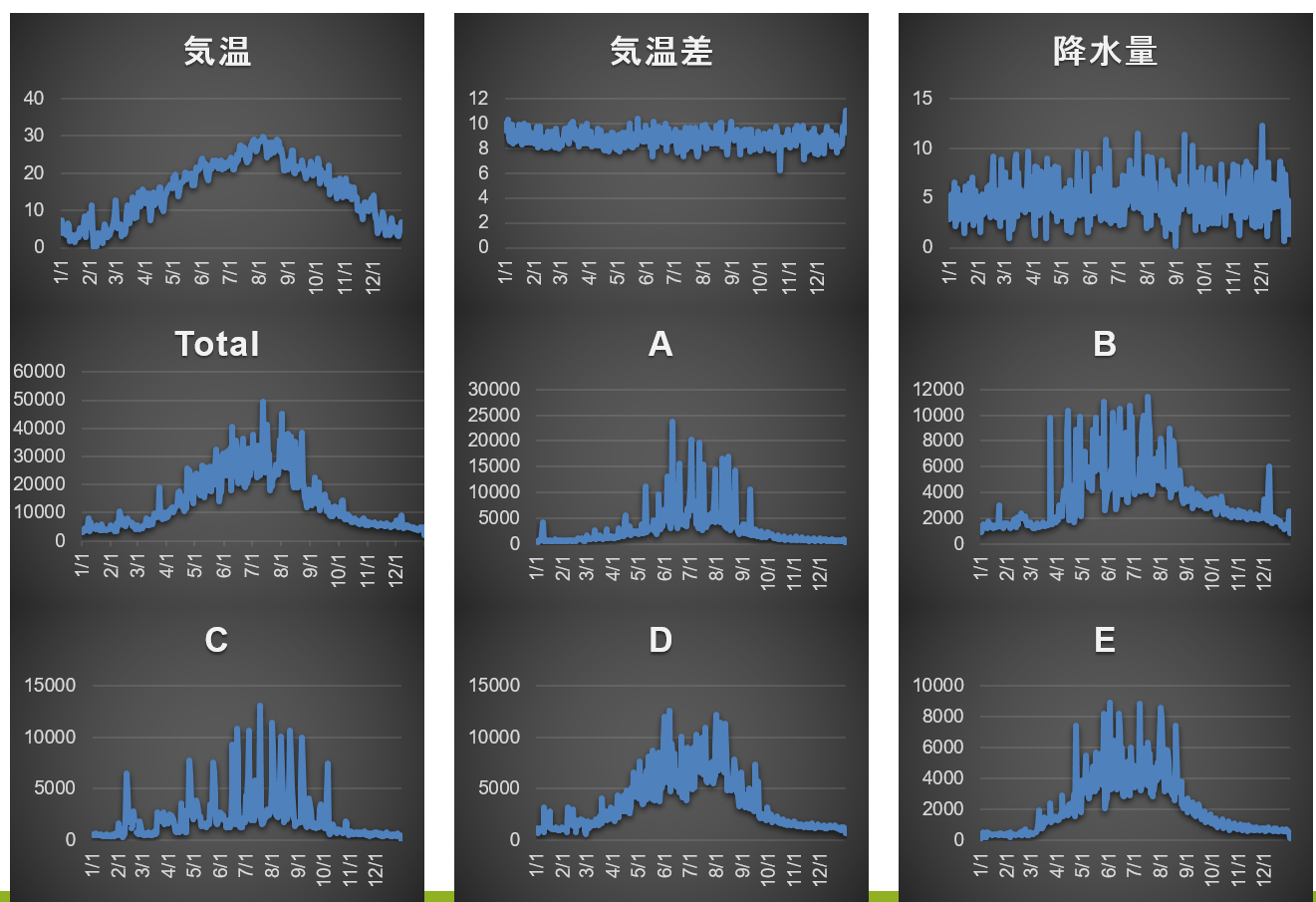
図Total、A、B、C、D、Eの真ん中部分の変動は激しい。一方、気温、気温差、降水量の変動はそんなに差はない。直観に、誤差項の分散は同じではないと判断します。では、検定してみましょう。
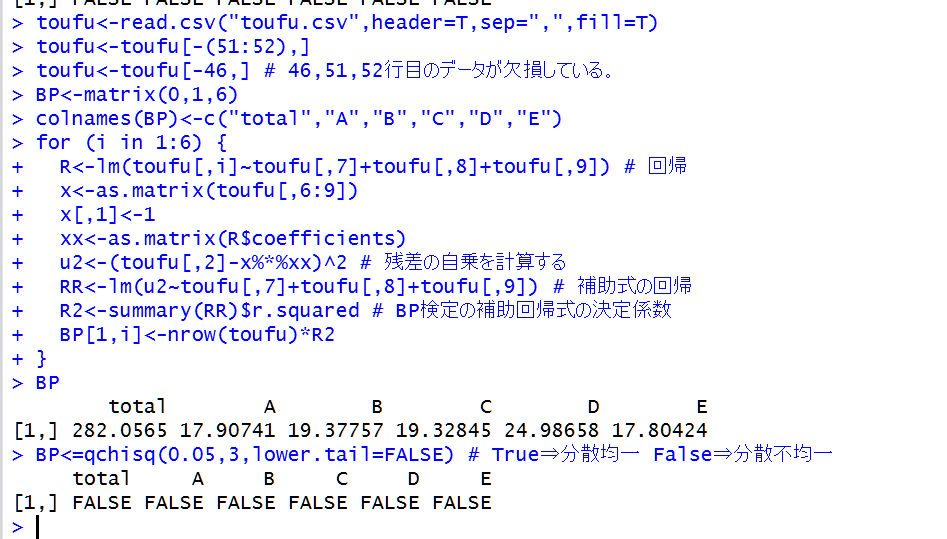
検定の結果は、分散不均一であることが分かりました。
コードを添付します。
BP.rb
# データの読み取り
tofu<-read.csv("tofu.csv",header=T,sep=",",fill=T)
# 欠損値の処理
tofu<-tofu[-(51:52),]
tofu<-tofu[-46,]
BP<-matrix(0,1,6)
colnames(BP)<-c("total","A","B","C","D","E")
for (i in 1:6) {
# 回帰
R<-lm(tofu[,i]~tofu[,7]+tofu[,8]+tofu[,9])
x<-as.matrix(tofu[,6:9])
x[,1]<-1
xx<-as.matrix(R$coefficients)
# 残差の自乗を計算する
u2<-(tofu[,2]-x%*%xx)^2
# 補助式の回帰
RR<-lm(u2~tofu[,7]+tofu[,8]+tofu[,9])
# BP検定の補助回帰式の決定係数
R2<-summary(RR)$r.squared
BP[1,i]<-nrow(tofu)*R2
}
# True⇒分散均一 False⇒分散不均一
BP<=qchisq(0.05,3,lower.tail=FALSE)