Union-Find木を利用した無向グラフの閉路検出

本記事でしたいこと

下図のように無向グラフが与えられた時にその中に閉路があるかどうか判定します．

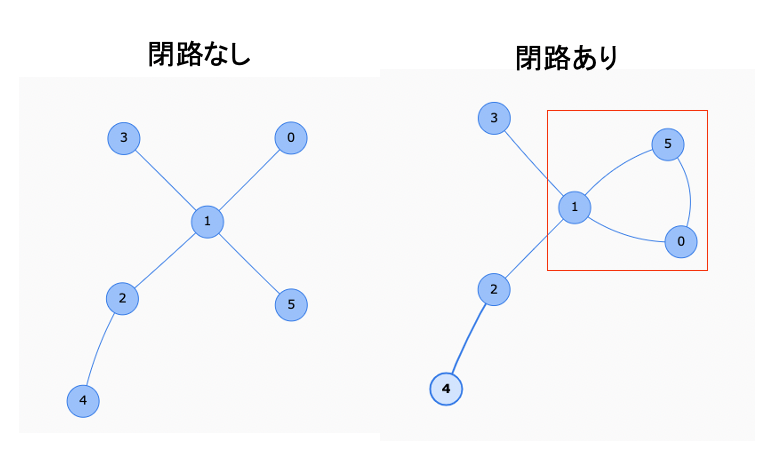
(画像はgenerate DOTを利用し作成しました)

方法１ : DFS(深さ優先探索)で解く

このようなルールで解けます．

1. 今いるノードからつながっているノードへ移動する．ただし，一つ前にいたノードへは戻らない．
2. 今いるノードに過去一度でも通っていたら閉路である．
3. 閉路があると判定できなかったら閉路はない．

DFSのソースコード

vector<int> isPassed(101010, false);
vector<vector<int>> graph(101010);

// dfs(今いるノード, 一つ前にいたノード)
bool dfs(const int current, const int before) {
    isPassed[current] = true;
    for(int i = 0; i < graph[current].size(); i++) {
        if(graph[current][i] == before) {
            // 前のノードに戻る場合
            continue;
        }
        if(isPassed[ graph[current][i] ]) {
            // 次に行くノードがかこに通ったことがある場合
            return true;
        }
        if(dfs(graph[current][i], current)) {
            return true;
        }
    }
    return false;
}
 
int main() {
    
    int n, m;
    cin >> n >> m;

    rep(i, m){
        int a, b;
        cin >> a >> b;
        graph[a].push_back(b);
        graph[b].push_back(a);
    }

    bool hasLoop = dfs(0, -1);
    if(hasLoop) {
        cout << "閉路があります" << endl;
    } else {
        cout << "閉路はありません" << endl;
    }
}

これでもいいのですが，個人的には課題があります．

1. もっと楽にできないか？
2. 以下のような問題の場合は同じ時間で解けない．

N個のノードがあります．このノードにM個の辺を張ります．各辺を張った時点で閉路があるか判定し，結果を出力してください(同じ辺はないものとします)．

入力
N M
A_0 B_0
A_1 B_1
...
A_M B_M

入力例
6 6
0 1
1 2
1 5
1 3
0 5
2 4

出力例
No
No
No
No
Yes
Yes

そこで，Union-Find木を使います．

方法２ : Union-Find木で解く

Union-Find木の場合，以下のルールで解くことができます．

1. 入力される辺を($A_i$, $B_i$)とします．
2. Union-Find木を利用して$A_i$, $B_i$の親(グループ番号)を調べます．これを$G_A$, $G_B$とします．
3. $G_A=G_B$の時，この辺($A_i$, $B_i$)を張った時点で閉路が発生します．

Union-Find木は長いのでスニペットにでも登録しておくと一瞬で呼び出せます．(参考:【競プロ】AtCoder早解きテクニック10選 (灰 ~ 緑コーダー向け))

Union-Find木のソースコード

class UnionFind {
public:
    // 親の番号を格納する。親だった場合は-(その集合のサイズ)
    vector<int> Parent;

    UnionFind(int N) {
        Parent = vector<int>(N, -1);
    }

    // Aがどのグループに属しているか調べる
    int root(int A) {
        if (Parent[A] < 0) return A;
        return Parent[A] = root(Parent[A]);
    }

    // 自分のいるグループの頂点数を調べる
    int size(int A) {
        return -Parent[root(A)];//親をとってきたい]
    }

    // AとBをくっ付ける
    bool connect(int A, int B) {
        // AとBを直接つなぐのではなく、root(A)にroot(B)をくっつける
        A = root(A);
        B = root(B);
        if (A == B) {
            //すでにくっついてるからくっ付けない
            return false;
        }

        // 大きい方(A)に小さいほう(B)をくっ付ける
        // 大小が逆だったらひっくり返す
        if (size(A) < size(B)) {
            swap(A, B);
        }

        // Aのサイズを更新する
        Parent[A] += Parent[B];
        // Bの親をAに変更する
        Parent[B] = A;

        return true;
    }
};

int main() {
    int n, m;
    cin >> n >> m;

    UnionFind uni(n);

    bool hasLoop = false;

    rep(i, m) {
        int a, b;
        cin >> a >> b;
        if(uni.root(a) == uni.root(b)) {
            hasLoop = true;
        }
        if(hasLoop) {
            cout << "Yes" << endl;
        } else {
            cout << "No" << endl;
        }
        uni.connect(a, b);
    }
}

いかがでしょう．これならすっきりしててミス無く書けそうです．

まずはこの計算量を考えてみましょう．
DFSは全ての頂点を探索するので$O(N + M)$です．
Union-Find木は$M$個の辺に対してconnect処理を行うので$O(N + Mα(N))$です．ただし，$α$はアッカーマン関数の逆関数で，詳しくはこちらの記事を参照してください．ほとんど$O(1)$と近似して問題ありません．

つまり，ほぼ同じ計算量で動きます．

Union-Find木でできる証明

また，Union-Find木でできる正当性を証明します．

1.二頂点が同じ親(グループ)の時

ここで，繋ぎたい辺を($A_0$, $A_1$)，$A_0$の親を$A_2$，$A_1$の親を$A_3$とします．
$A_0$, $A_1$は必ずどこかの頂点と結ばれています．ここでは$A_0=A_3$，$A_1=A_2$，$A_2=A_3$の可能性もあります．

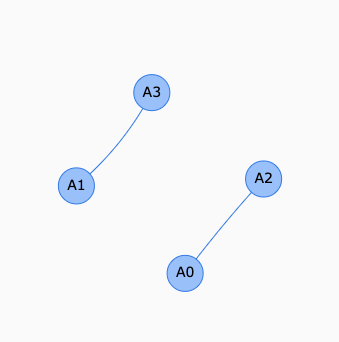
仮定上$A_2$, $A_3$間は同じ親(グループ)なのでなんらかの経路を辿って行くことができます．

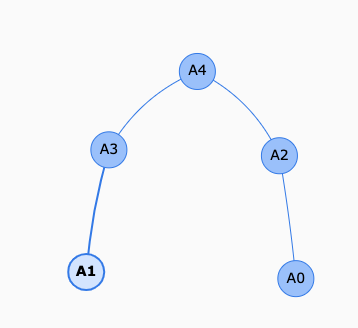
つまり，辺($A_0$, $A_1$)を貼ると閉路ができます．

2.二頂点が違う親(グループ)の時

ここで，繋ぎたい辺を($A_0$, $B_0$)とします．

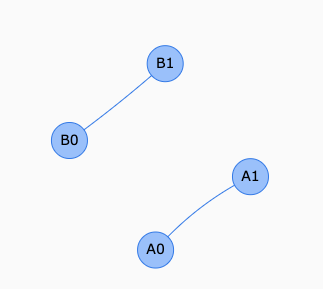
このように二つの親(グループ)が違う$=$二つのグループ間の経路がないので，辺($A_0$, $B_0$)を張っても閉路ができません．

例題

ARC-B バウムテスト
閉路検出+グラフの数も答えなければいけません．DFSだと面倒ですが，Union-Find木を使えば簡単だと思います．