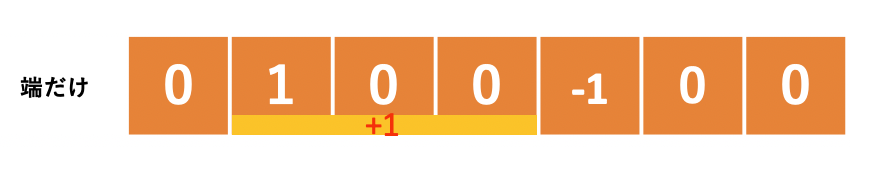問題概要
配列Aに対して次の二つのクエリを処理してください
- $add(s,t,x)$: $A_s,A_{s+1},...,A_t$に$x$を加算する。
- $get(i)$: $A_i$の値を出力する。
※最初にAの要素は0で初期化します.
入力
n q
query
queryはaddの場合0 s t x,getの場合1 iと入力されます.
制約
n < 100000
q < 100000
x < 1000
1 <= s <= t <= n
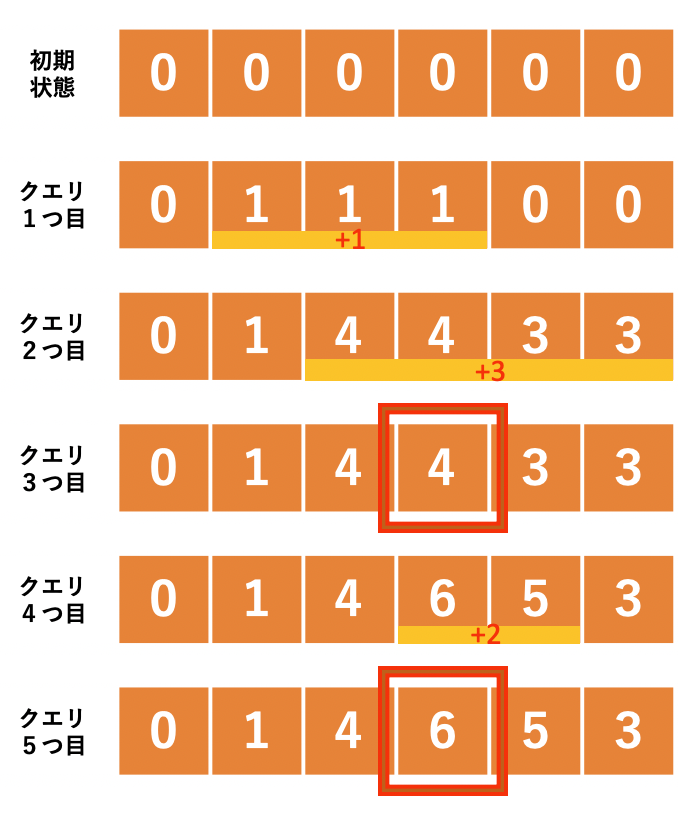
大体このような感じです.例えば入力が以下のような場合,下図のように処理します.
入力例
6 5
0 2 4 1
0 3 6 3
1 4
0 4 5 2
1 4
出力例
4
6
赤枠が出力するものです.
解説
例えば配列の2番目から4番目を1足すという処理は1を3回代入するのではなく,配列の2箇所に1と-1を代入します.(配列のサイズが1つ多い事に関しては後述します.)
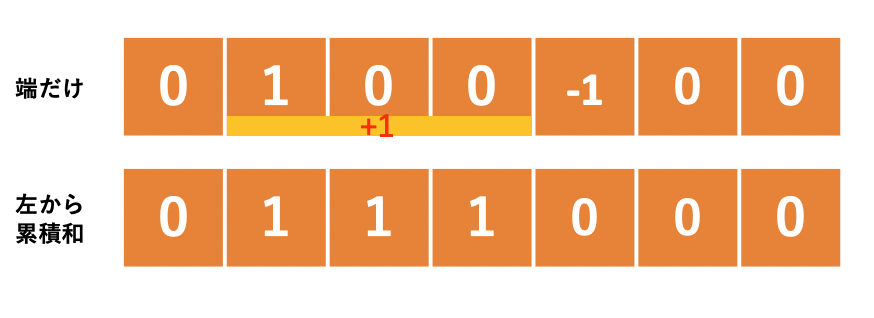
このようにした後,左から累積和をとると嬉しいことがわかります.(累積和は左から順番に足していくアルゴリズムですが,詳しくはこの記事を参照してください.)
この累積和をとる処理が定数時間でできれば解けそうです.
ここで,セグメント木を使います.セグメント木の詳細な解説に関しては割愛します.(私の簡潔な説明ならこちらの記事や,北海道大学さんのこちらの記事を参照してください.)
セグメント木のできることとして,以下のものがあります.
- サイズ$N$の配列の区間[$s$, $t$)の和を$O(\log{N})$で計算する
ここで,$s=1$とすると左から$t$個の累積和が取得できます.よってこの問題が解けそうです.そこで先ほどの
配列の2箇所に1と-1を代入します.
をもっと一般化します.
- 区間[$s$,$t$)に$x$を足したい時 : $A_s=A_s+x$ と $A_t=A_t-x$ をします.
- $A_i$の値が知りたい時 : セグメント木で区間[1, $i$)の和を求めます.
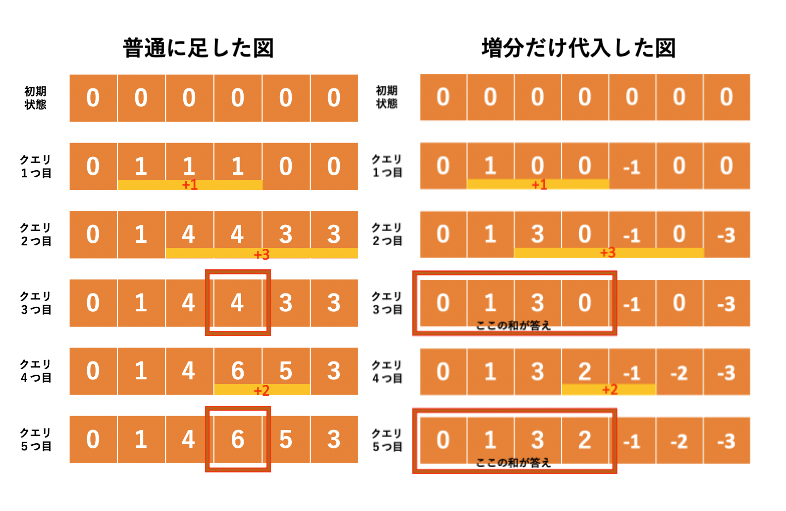
これを先ほどの入力例でやってみます.
左の図の赤枠が右の図の赤枠の合計と一致しています.ここでわかるのですが,$A_t=A_t-x$の処理をする際,$t$は$N$より1つ大きくなることがあります.よって配列のサイズは$N+1$以上にすべきです.
結論
- $add(s,t,x)$: $A_s,A_{s+1},...,A_t$に$x$を加算する。
が来た時は以下の処理を実行します.(※このクエリの右端は閉区間です.)
A[s] += x;
A[t + 1] -= x;
- $get(i)$: $A_i$の値を出力する。
このクエリが来た時はセグメント木の機能を使います.
SegmentTree st;
printf("%d\n", st.query(0, i));
実装
コードはこのようになります.セグメント木のコードは長いので隠します.
セグメント木のコード
template <typename T>
class Sum {
public:
// 単位元
T unit;
Sum(void) {
// 単位元
unit = 0;
}
// 演算関数
T calc(T a, T b) {
return a + b;
}
};
template <typename T, class MONOID>
class SegmentTree {
public:
// セグメント木の葉の要素数
int n;
// セグメント木
vector<T> tree;
// モノイド
MONOID mono;
SegmentTree(vector<T> &v) : n(1 << (int)ceil(log2(v.size()))), tree(vector<T>(n << 1)) {
for(int i = 0; i < v.size(); ++i) {
update(i, v[i]);
}
for(int i = v.size(); i < n; ++i) {
update(i, mono.unit);
}
}
// k番目の値(0-indexed)をxに変更
void update(int k, T x) {
k += n;
tree[k] = x;
for(k = k >> 1; k > 0; k >>= 1){
tree[k] = mono.calc(tree[k << 1 | 0], tree[k << 1 | 1]);
}
}
// [s, t)の最小値(0-indexed)を求める.
T query(int s, int t) {
T res = mono.unit;
s += n;
t += n;
while(s < t) {
if(s & 1) {
res = mono.calc(res, tree[s++]);
}
if(r & 1) {
res = mono.calc(res, tree[--t]);
}
s >>= 1;
t >>= 1;
}
return res;
}
T operator[](int k) {
// st[i]で添字iの要素の値を返す
if(k - n >= 0 || k < 0) {
return -INF;
}
return tree[tree.size() - n + k];
}
};
int main() {
int n, q;
int query, s, t, x, i;
cin >> n >> q;
// セグメント木の作成
vi v(n + 1);
SegmentTree<int, Sum<int> > st(v);
while(q--) {
scanf("%d", &query);
if(query) {
// クエリget(i)の時
scanf("%d", &i);
printf("%d\n", st.query(0, i));
} else {
// クエリadd(s, t, x)の時
scanf("%d %d %d", &s, &t, &x);
// 私のセグメント木の更新処理は加算ではなく代入なので,
// これはs - 1番目の値をx足しているのと同義です.
st.update(s - 1, st[s - 1] + x);
st.update(t, st[t] - x);
}
}
}
例題
ほとんど一緒です.最後までご覧いただきありがとうございました.
AOJ-データの集合とクエリ処理2_E-Range Add Query