発端
twitter を眺めていたら以下のツイートを発見しました.
3時間に及ぶ試行錯誤の末,たった1つの数式で3Dの「ポン・デ・リング」を表示することに成功.(2Dのもあるよ) pic.twitter.com/r23phIA4hp
— CHARTMAN (@CHARTMANq) December 27, 2017
@CHARTMANq さんによる「ポン・デ・リング関数」です.球体が 8 つつながった形状をしていますが,ひとつの数式で表現されています.とても美しいです.
$$
\left(\sqrt{x^2+y^2} - 8 - \left| \left(\frac{x^2-y^2}{x^2+y^2}\right)^2 - \frac{1}{2} \right|\right)^2
- z^2 =
\left(2 + 3\left| \left(\frac{x^2-y^2}{x^2+y^2}\right)^2 - \frac{1}{2} \right| \right)^2
$$
せっかくなので「ポン・デ・リング関数」を gnuplot で再現してみたいと思います.
陰関数表示からパラメタ表示への変換
先ほどの方程式は陰関数表示1になっています.gnuplot で 3 次元プロットをするときに使う splot という命令は以下のように使うため基本的には陽関数しか表現できません.
splot Z(x,y) t "Z は座標 (x,y) での z 座標を返す関数"
そのため閉曲面のような多価関数を表現することには向いていません.gnuplot で球体のような曲面を表現するためにはパラメタ表示を使います.詳しい使い方は gnuplot の公式のデモページやヘルプ参照してください.
set parametric
set xrange [-1.5:1.5]
set yrange [-1.5:1.5]
set zrange [-1.5:1.5]
set urange [0:2*pi]
set vrange [0:2*pi]
set isosample 30 # 3D plot で使用するメッシュの細かさを指定する
set ticslevel 0 # 3D plot で z 軸の余計なスペースを消す
set view equal xyz # 3D plot で軸の縮尺を同一にする
splot cos(u)*cos(v),sin(u)*cos(v),sin(v) \
t "(u,v) を引数にとって x,y,z 座標を返す関数をそれぞれ与える"
ここではこの set parametric を利用してプロットを作成していきます.
「ポン・デ・リング関数」は z 軸まわりに 8 回対象2です.このためまずは z 軸まわりに極座標で表現すると簡単に表現できそうです.$x = r\cos\theta$, $y = r\sin\theta$ と置いて代入します.
$$
\left(r - 8 - \left| \left(\cos^2\theta - \sin^2\theta\right)^2 - \frac{1}{2} \right|\right)^2
- z^2 =
\left(2 + 3\left| \left(\cos^2\theta - \sin^2\theta\right)^2 - \frac{1}{2} \right| \right)^2
$$
もう少し変形します.
$$
\left(r - 8 - \frac{1}{2}\left| \cos{4\theta} \right|\right)^2 + z^2 =
\left(2 + \frac{3}{2}\left| \cos{4\theta} \right| \right)^2
$$
関数を定義してもう少しシンプルな見た目なにします.
$$
\bigl(r - C(\theta) \bigr)^2 + z^2 = R(\theta)^2
$$
$\theta$ を無視して $r$, $z$ だけに注目するとこれは中心が $(r,z) = \bigl(C(\theta),0\bigr)$ で半径が $R(\theta)$ の円を表しています.「ポン・デ・リング関数」で表される図形を $\theta$ 方向に切った断面は常に円になっているということです.今回はこのことを利用して「ポン・デ・リング関数」を可視化します.
gnuplot によるポン・デ・リングの可視化
まずは $R(\theta)$ を定義します.以下の式を実行するとポン・デ・リングの芯をプロットすることができます.
C(u,v) = 8 + 0.5*abs(cos(4*u))
X(u,v) = C(u,v)*cos(u)
Y(u,v) = C(u,v)*sin(u)
Z(u,v) = 0
set xrange [-15:15]
set yrange [-15:15]
set zrange [-4.5:4.5]
set grid x y
set isosample 30 # 3D plot で使用するメッシュの細かさを指定する
set ticslevel 0 # 3D plot で z 軸の余計なスペースを消す
set view equal xyz # 3D plot で軸の縮尺を同一にする
set hidden3d # 3D plot で陰線処理を有効に(重たくなるので注意)
splot X(u,v),Y(u,v),Z(u,v) t "ポン・デ・リングの芯だけをプロット"
あとはこの芯にポン・デ・リングの肉をつけていきます.
R(u,v) = 2 + 1.5*abs(cos(4*u))
C(u,v) = 8 + 0.5*abs(cos(4*u))
X(u,v) = (C(u,v)+R(u,v)*cos(v))*cos(u)
Y(u,v) = (C(u,v)+R(u,v)*cos(v))*sin(u)
Z(u,v) = R(u,v)*sin(v)
set xrange [-15:15]
set yrange [-15:15]
set zrange [-4.5:4.5]
set grid x y
set isosample 50 # 3D plot で使用するメッシュの細かさを指定する
set ticslevel 0 # 3D plot で z 軸の余計なスペースを消す
set view equal xyz # 3D plot で軸の縮尺を同一にする
set hidden3d # 3D plot で陰線処理を有効に(重たくなるので注意)
splot X(u,v),Y(u,v),Z(u,v) t "ポン・デ・リングをプロット"
あとは適当に見た目を整えます.満足のいく結果が出たら isosample の値を大きくしてメッシュを細かくして完成です.
R(u,v) = 2 + 1.5*abs(cos(4*u))
C(u,v) = 8 + 0.5*abs(cos(4*u))
X(u,v) = (C(u,v)+R(u,v)*cos(v))*cos(u)
Y(u,v) = (C(u,v)+R(u,v)*cos(v))*sin(u)
Z(u,v) = R(u,v)*sin(v)
set xtics format ""; set ytics format ""; set ztics format ""
set xrange [-15:15]; set yrange [-15:15]; set zrange [-4.5:4.5]
set cbr [-3.5:3.5]
set grid x y
set contour; set cntrparam levels discrete 0
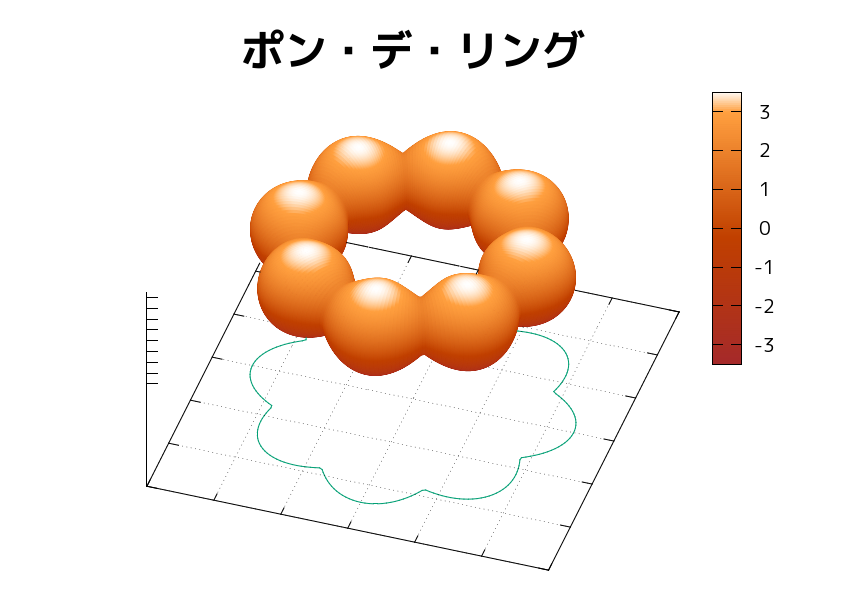
set title "ポン・デ・リング" font "M+ 1c Bold, 32" offset 0,-5
set isosample 250 # 3D plot で使用するメッシュの細かさを指定する
set ticslevel 1.0 # 3D plot で z 軸のスペースを調整
set view equal xyz # 3D plot で軸の縮尺を同一にする
set hidden3d # 3D plot で陰線処理を有効に(重たくなるので注意)
set pm3d depthorder # 3D plot (pm3d) で視線方向の奥行を考慮
set palette define (-3.5 'brown', -0.5 'dark-orange', 2.5 'tan1', 3 'white')
splot X(u,v),Y(u,v),Z(u,v) w pm3d not