はじめに
gnuplot はサイエンスでも使われる有名なプロットソフトウェアです.最近では Python+matplotlib などが主流になりつつありますが,gnuplot 単体でも多少がんばればそれなりにのプロットを作成することもできるものです.そこで,今回は gnuplot 初心者に向けて,gnuplot がちょっと便利になる基本的なテクニックを紹介します.
目標
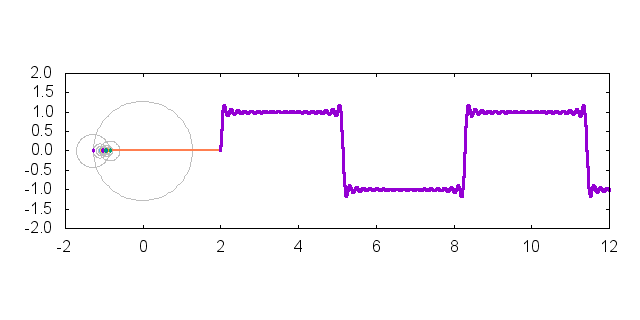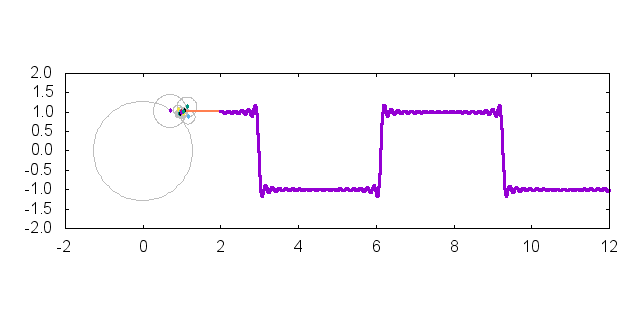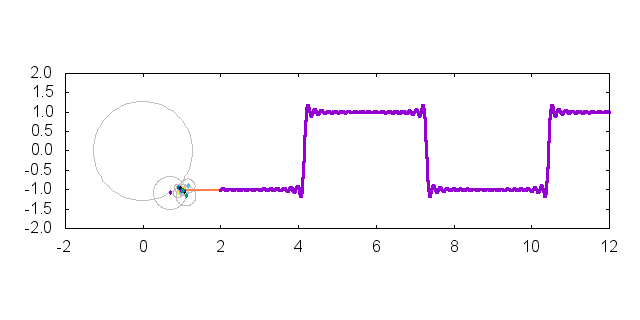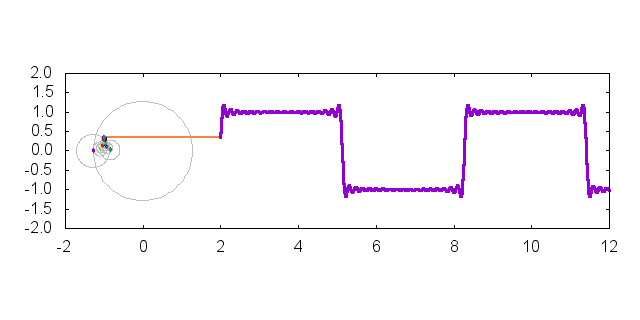
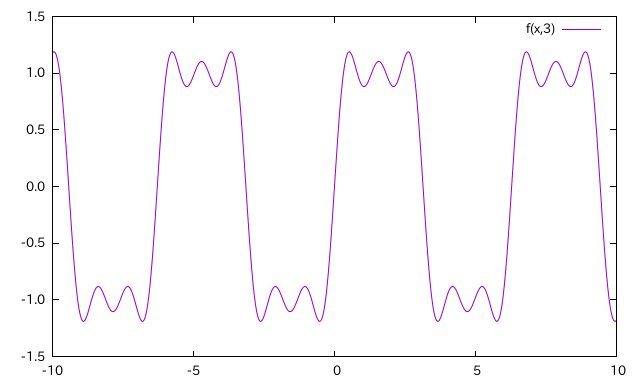
今回はこんな感じのプロット作成するためのテクニックを紹介します.元ネタは Twitter で見た"これ"です.矩形波をフーリエ級数展開して可視化しています.使用したバージョンは gnuplot-5.0.0 です.ただし,本稿で使用しているほとんどの機能は gnuplot-4.6.x でも使用可能です.
再帰関数 or sum 記法
矩形波をフーリエ級数展開すると以下の式で表現できます.
f(x) = \sum_{n=1}^\infty \frac{4}{\pi(2n-1)}\sin\left((2n-1)x\right)
無限大まで足すわけにはいかないので,これを適当なところまで足した関数 $f_N(x)$ を作成することにします.
f_N(x) = \sum_{n=1}^N \frac{4}{\pi(2n-1)}\sin\left((2n-1)x\right)
このように和の形式で定義されている関数を gnuplot で用いるためには,まず再帰を利用する手法が考えられます.関数 f(x,n) は以下のように定義できます.
f(x,n) = (n==0)?0:4.0/pi/(2*n-1)*sin((2*n-1)*x)+f(x,n-1)
この定義では n に非負整数以外を入れると再帰が止まらずに stack overflow を起こしてしまうことに注意してください.同様の関数は sum 記法を用いても定義できます.sum 記法は最近導入された手法ですが,現在比較的広く利用されている gnuplot-4.6 にはすでに導入されています. sum 記法を使った場合には以下の表記をします.
f(x,n) = sum [m=1:n] 4.0/pi/(2*m-1)*sin((2*m-1)*x)
数学的な定義とかなり近い表記になりました.どちらを使用してもいいと思います.なお,この sum 記法は関数定義以外でも用いることができます.以下は $\pi$ の近似値を計算したものです.
print sum [i=1:1000] 4.0*(-1)**(i+1)/(2*i-1)
# 3.14059265383979
これで矩形波のフーリエ級数展開を表現した関数の定義ができました.次は回転する円の部分に注目しましょう.
set parametric
円周上を移動する点を表現するにはどうしても二価関数を使うことになります.parametric を設定して $x,y$ 座標を別々に与えましょう.
set parametric # dummy 変数が t になる
parametric を設定するとダミー変数が t になります.プロットでは $x,y$ 座標を表す関数(数値)を独立に与えます.$x$ 座標は何でもいいのですが元ネタに合わせて位相を $\pi/2$ だけずらした関数にすることにしました.
# わかりやすくするために関数を定義
y(t,n) = f(t,n)
x(t,n) = f(t-pi/2.0,n)
set size ratio -1 # x,y 座標を同じスケールにする
set sample 1e3 # サンプル点を 1000 個にする
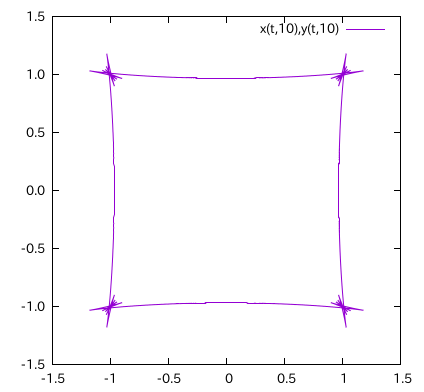
plot x(t,10),y(t,10) w line
以下のような正方形に近い図形がプロットされるはずです.正方形の上を動点が等速で移動することを考えると,動点の $x,y$ 座標が矩形波に対応していることが分かります.
do 記法による繰り返し
それでは動点を動かしてみましょう.そのためには do 記法を使うと便利です.do 記法も gnuplot-4.6 以降であれば問題なく利用できます.
# 1 点だけプロットするので範囲を明示する必要がある
set xrange [-1.5:1.5]
set yrange [-1.5:1.5]
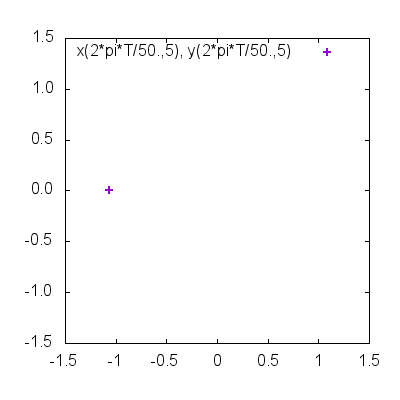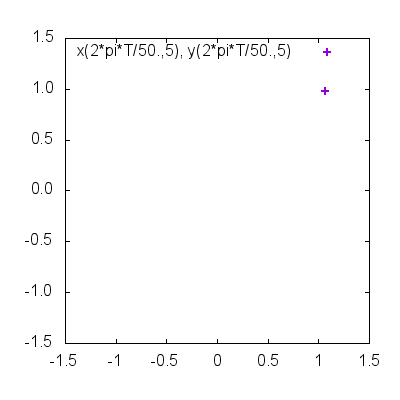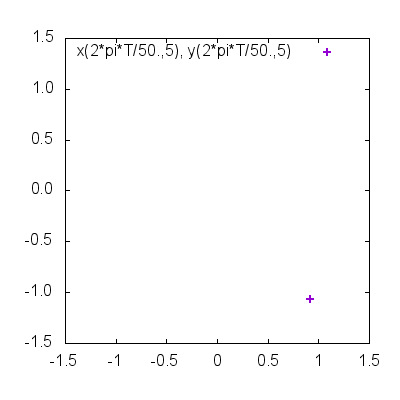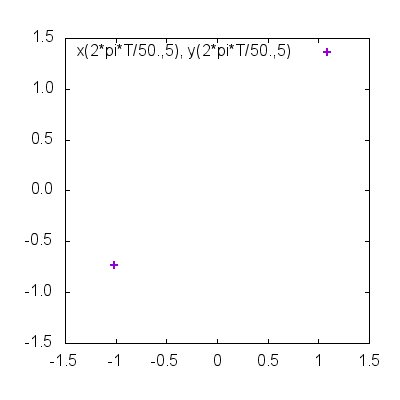
do for [T=0:49] {
plot x(2*pi*T/50.,5), y(2*pi*T/50.,5) w p lw 2
}
動点が領域内を動き回る様子が確認できたでしょうか?
gif アニメーション出力
せっかくなので gif アニメーションに書き出してみましょう.set terminal で gif を指定,オプションに animate を指定することで,連続して書きだしたプロットが gi作成したプロット
f アニメーションになります.
set terminal gif anim
set output "anim.gif"
do for [T=0:49] { plot x(2*pi*T/50.,5), y(2*pi*T/50.,5) w p lw 2 }
unset output
plot 内部の for 記法でまとめてプロット
動点を複数の n についてプロットしてみましょう.
plot \
x(2*pi*T/100.,1), y(2*pi*T/100.,1) w p, \
x(2*pi*T/100.,2), y(2*pi*T/100.,2) w p, \
x(2*pi*T/100.,3), y(2*pi*T/100.,3) w p, \
x(2*pi*T/100.,4), y(2*pi*T/100.,4) w p, \
x(2*pi*T/100.,5), y(2*pi*T/100.,5) w p
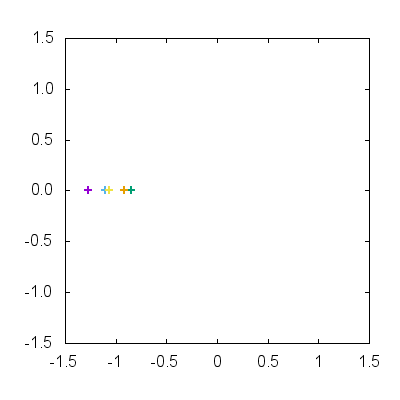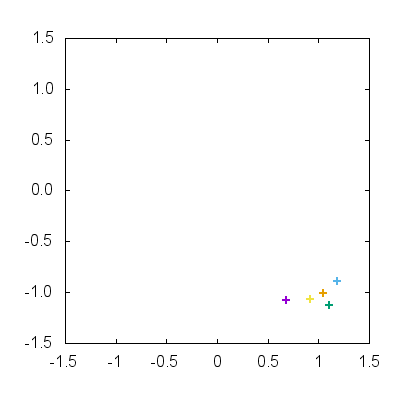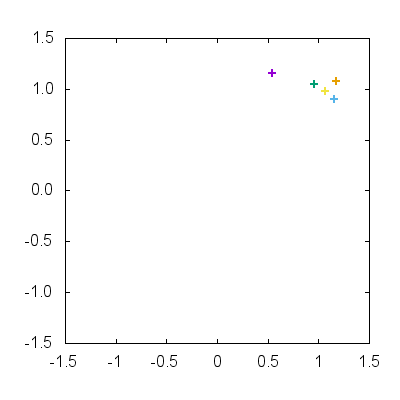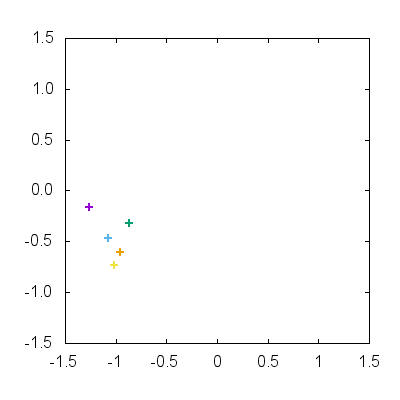
もちろん上記の方法でもいいですが,似たようなプロット命令を何度も繰り返すのは不格好ですし,ちょっとした修正が必要になったときに大変面倒になります.ここでは plot 内部で for 記法を用いることで表記を簡略化しましょう.
plot for [n=1:5] x(2*pi*T/100.,n), y(2*pi*T/100.,n) w p
plot 内 for 記法によって比較的スマートに記述することができます.先ほどの do 記法と組み合わせることによって多数の動点が一度に動きまわる様子を gif アニメーションで可視化できます.
set terminal gif amimate
set output "amim.gif"
do for [T=0:99] {
plot for [n=1:5] x(2*pi*T/50.,n), y(2*pi*T/50.,n) w p pt 1 lw 2 notitle
}
unset output
まとめ
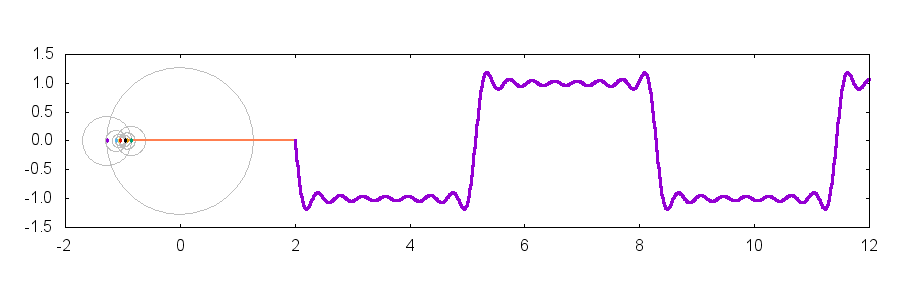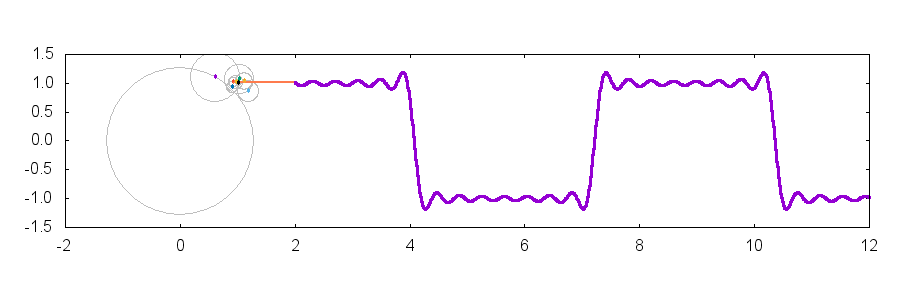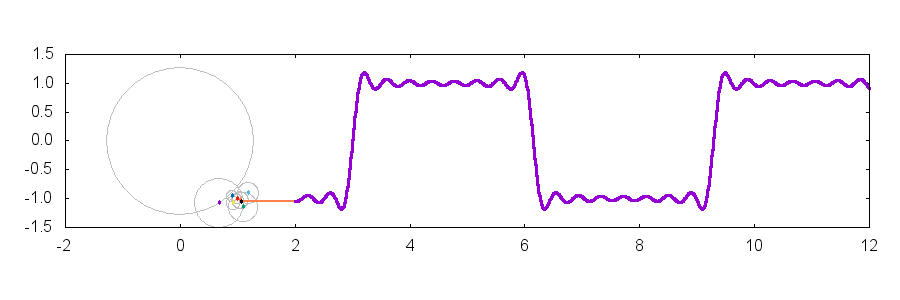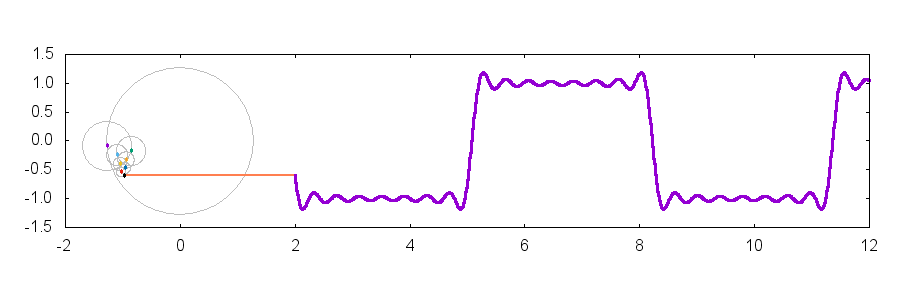
以上のテクニックを組み合わせてみましょう.冒頭の gif アニメーションは以下のようなコマンドによって生成することができます.set object でちょっとした装飾を加えていますが,上記のテクニックを組み合わせるだけで描くことができます.
set term gif amim size 640,300
set output "anim.gif"
set parametric # ダミー変数は t です
set xrange [-2:12]
set yrange [-2:2]
set trange [0:10]
set size ratio -1
set sample 1e3
# ここでは第 8 項まで足します
N = 8
do for [T=0:99] {
do for [m=1:N] {
# 動点に合わせて背景の円を描きます
set object m circle at x(2*pi*T/100.,m-1),y(2*pi*T/100.,m-1) \
size 4.0/pi/(2*m-1) fc rgb "gray" fs empty border
}
# 横方向のラインを描きます
set arrow 1 nohead from x(2*pi*T/100.,N),y(2*pi*T/100.,N) \
to 2.0,y(2*pi*T/100.,N) lc rgb "coral" lw 2
plot \
for [n=1:N] \
x(2*pi*T/100.,n),y(2*pi*T/100.,n) w p pt 7 ps .5 notitle, \
t+2, y(2*pi*T/100.-t,N) w l lw 3 lc 1 notitle
}
}
unset output
上記のコマンドで作成したプロットを以下に貼り付けます.