目的
球面を平面に投影する方法としてもっともポピュラーなものはメルカトル図法ではないかと思います.緯度方向と経度方向が直行するので図示するのはとても簡単です.一方で,極に近い部分では形状が大きく歪むという点もメルカトル図法の特徴です.
メルカトル図法で表現された平面上で,ある点を中心とした角半径 θ の円を描くことを考えます.このとき,緯度経度平面上で角半径 θ の円を描いてはいけません.半径 θ とはあくまで球面上で定義されるものだからです.円を構成する各点の座標を何とかして求める必要があります.
今更気づきましたがこれメルカトル図法じゃないですね……正しくは Equirectangular projection です. Mercator projection との違いについては末尾の Wikipedia へのリンクを参照してください.
解決方法
方針は次のとおりです.まずは,円を最も描きやすい場所で考えます.緯度 α - 経度 δ ととった系で円を描くには極が最も簡単です.まずは極を中心として半径 θ の円を描きます.その後,円の中心が指定された位置に来るように座標系を回転させます.座標系の回転には回転行列を用います.最終的に次のようなスクリプトを作成しました.
# !/usr/local/bin/gnuplot
#
set mxtics 5
set mytics 4
set grid front
set grid x y mx my
set grid lt 0 lw 1 lc rgb 'gray40', lt 0 lc rgb 'gray60'
set key samplen 2
set xtics format "%.0f" offset 0,0.2
set xlabel "Lon (degree)" offset 0,0.1
set xrange [ 0.0000 : 360.0000 ] reverse
set ytics format "%+4.0f" offset 0.2,0
set ylabel "Lat (degree)" offset 0.8,0
set yrange [ -90.0000 : 90.00000 ] noreverse
rad2deg(r) = 180.*(r/(4.*atan(1.)));
deg2rad(d) = (d/180.)*4.*atan(1.);
ad2x(a,d) = cos(a)*cos(d)
ad2y(a,d) = sin(a)*cos(d)
ad2z(a,d) = sin(d)
xyz2a(x,y,z) = atan2(x,y)+pi
xyz2d(x,y,z) = asin(z)
euler1a(p,a,d) = \
xyz2a(cos(p)*ad2x(a,d)-sin(p)*ad2y(a,d),\
sin(p)*ad2x(a,d)+cos(p)*ad2y(a,d),\
ad2z(a,d))
euler1d(p,a,d) = \
xyz2d(cos(p)*ad2x(a,d)-sin(p)*ad2y(a,d),\
sin(p)*ad2x(a,d)+cos(p)*ad2y(a,d),\
ad2z(a,d))
euler2a(p,a,d) = \
xyz2a(ad2x(a,d),\
cos(p)*ad2y(a,d)-sin(p)*ad2z(a,d),\
sin(p)*ad2y(a,d)+cos(p)*ad2z(a,d))
euler2d(p,a,d) = \
xyz2d(ad2x(a,d),\
cos(p)*ad2y(a,d)-sin(p)*ad2z(a,d),\
sin(p)*ad2y(a,d)+cos(p)*ad2z(a,d))
euler3a(p,a,d) = \
xyz2a(cos(p)*ad2x(a,d)-sin(p)*ad2y(a,d),\
sin(p)*ad2x(a,d)+cos(p)*ad2y(a,d),\
ad2z(a,d))
euler3d(p,a,d) = \
xyz2d(cos(p)*ad2x(a,d)-sin(p)*ad2y(a,d),\
sin(p)*ad2x(a,d)+cos(p)*ad2y(a,d),\
ad2z(a,d))
###
alpha1(x,y) = euler1a(atan2(x,y),0,pi/2-sqrt(x**2+y**2))
delta1(x,y) = euler1d(atan2(x,y),0,pi/2-sqrt(x**2+y**2))
alpha2(x,y,d) = euler2a(d-pi/2.0,alpha1(x,y),delta1(x,y))
delta2(x,y,d) = euler2d(d-pi/2.0,alpha1(x,y),delta1(x,y))
alpha3(x,y,a,d) = euler3a(-a+pi/2.0,alpha2(x,y,d),delta2(x,y,d))
delta3(x,y,a,d) = euler3d(-a+pi/2.0,alpha2(x,y,d),delta2(x,y,d))
alpha(x,y,a,d) = rad2deg(alpha3(deg2rad(x),deg2rad(y),deg2rad(a),deg2rad(d)))
delta(x,y,a,d) = rad2deg(delta3(deg2rad(x),deg2rad(y),deg2rad(a),deg2rad(d)))
set parametric
set tr [0:2*pi]
set sample 600
x(t) = 15*sin(t)
y(t) = 15*cos(t)
plot \
for [n=1:9] \
alpha(x(t),y(t),30+30*n,-100+20.*n),\
delta(x(t),y(t),30+30*n,-100+20.*n) \
w p notitle ps 0.2 lc rgb hsv(160+5*n,196,165+10*n)
# EOF
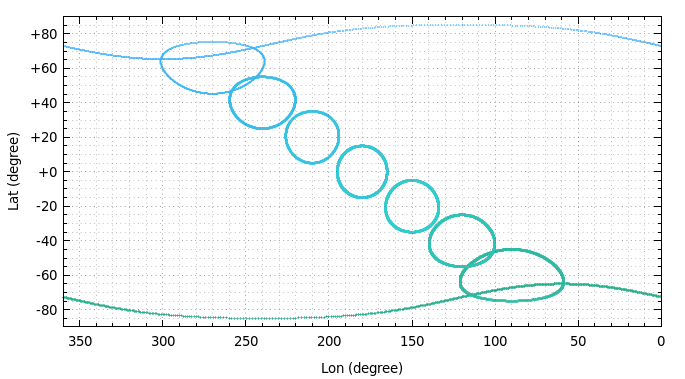
このスクリプトでは指定の位置に半径 15 度の円を描きます.中心の緯度は -80 から +80 度まで変化します.実際に wxt terminal で作図した結果を以下に表示します.極に近い部分では円の形状が大きくゆがんでいる様子が確認できます.
rad2deg, deg2rad は度数法と弧度方の変換に用いた関数です.ad2x, ad2y, ad2z という 3 つの関数は経度-緯度の形式 (α,δ) から (x,y,z) の表示に変換するためのものです.xyz2a,xyz2d は逆に (x,y,z) の形式から (α,δ) の表示に変換するための関数です.euler1a, euler1d という関数はオイラー角の形式で (α,δ) のペアを回転させる関数です.オイラー角に習って 3 ペアの関数がありますが euler1a, euler1d と euler3a, euler3d は本質的に同じ演算をしています.オイラー角の詳細については Wikipedia の オイラー角 の項を参照してください.また,色に指定に使用している hsv 関数については僕の過去の記事を参照してください.
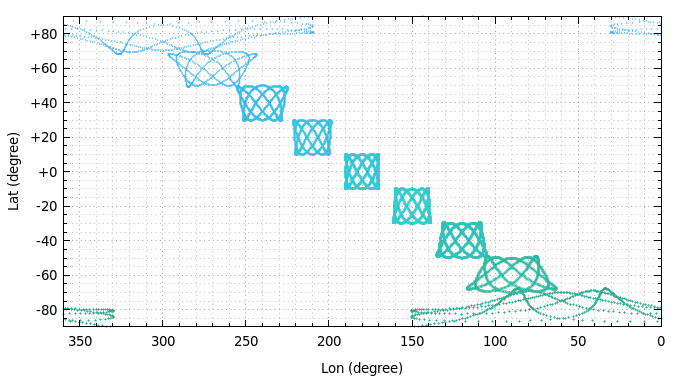
今回用いた手法は円以外の図形にも用いることができます.関数 x, y を以下のように変更すると,下記のようなプロットになります.
x(t) = 10*sin(3*t)
y(t) = 10*cos(5*t)
今回はなんとか目的のプロットを得ることができました.しかし,かなり力技で何とかした感じが否めないので,もしもっとエレガントな方法を知っている方がいらっしゃいましたらコメントしていただけるとうれしいです.また,今回作成したスクリプトはあまり詳細なテストをしていないのでバグがあるかもしれません.試してみて変な挙動を見せたら報告してくださるとありがたいです.