1.対象読者
データと言えば、分類、予測、機械学習!!!
ところが、どこに使えるかわからないけど収集してしまったデータって
ありませんか?
例えば私はロト6の一等データを見つめる日々を送っている。
全投入金額は確実に私の居住している場所に、役立ってしまっているのだ。
このロト6も今回で165〇を迎えている。
人間の意思や季節とは無関係に、放出される魔法の数字の組み合わせ。
こういうどこに使えるかわからない数字データに苛立ちを覚える人、
何よりも突然、散布図が見たくなった人
が対象です。
2.実行環境
Windows10 home
Python 3.8.10
jupyter notebook(セルごとに実行して確認できるので便利)
3.概要
当選数字の履歴(開始回から最大30件、開催回から終了回の間隔が30未満の場合は開催回~終了回)と、指定した開催回の間の当選数字の2つの数字の傾向を見ることを目標にしたカウント数散布図を作成している。
(1).当選データのcsvファイルを読み込み
(2).データ表示したい開催回(開始行とする)と集計終了回(終了行とする)を入力する
(3).開始行から30行分(終了行と開始行の間隔が30未満の時は、終了行-開始行分)のレコードデータを取得し、散布図にセット
(4).開始行~終了行の当選番号データを取得して、当選番号の2つの数字の組み合わせが期間内に何回登場したかカウントした一覧のdataframeの作成
| 数字1 | 数字2 | 数字3 | 数字4 | 数字5 | 数字6 |
|---|---|---|---|---|---|
| 1 | 4 | 5 | 40 | 42 | 43 |
| 2 | 4 | 5 | 19 | 23 | 37 |
| 4 | 5 | 19 | 31 | 37 | 39 |
1行の数字の組み合わせは15種類ある
((1,4),(1,5),(1,40),(1,42),(1,43),(4,5)...)
この数字の組み合わせが、他の行に何回登場したかを
表すデータ一覧を下記のように作成する
| 数字1 | 数字2 | カウント | クラス |
|---|---|---|---|
| 4 | 5 | 3 | A |
| 4 | 19 | 2 | B |
| 5 | 19 | 2 | B |
(5)(4)をカウント数で分類した散布図を表示
(カウント数に応じて,A,B,Cとクラス分けをしており、
A,Bのものを表示するようにした)
(6)(5)のデータを、どの区間でカウントしたかわかるようにcsvファイルに保存する。
4.メモ
既存のデータフレームから、そのデータを元に別のデータフレームを作って、グラブ表示するという地味な流れだが、中々大変だったのでメモとして残す。
(1)連想配列名={}
空の連想配列を宣言
例)dict_graph={}
(2)キー名 in 配列名
キーが配列に存在するかチェックする。
存在する場合はTrueを存在しない場合はFalseを返す。
例)key1 in dict_graph
(3)データフレーム名=pd.DataFrame()
空(indexも項目名も空)のデータフレームを作る
例)new_df2=pd.DataFrame()
(4)pd.Series([x1,x2,..,xn] ,index=['項目1',..,'項目n'])
行単位の項目名(index以降に設定)と項目に対応するデータの設定。
(5)データフレーム名.iloc[i行,j列]
1行1列など、列名や行名ではなく数字を指定して取得する時に使う。
例)val1=df0.iloc[1,2]
df0の2行3列のデータが取得できる。
特に列数が多い時などは、ilocしか勝たん!!
という状況になる。
(6)sns.scatterplot(x='x1', y='y1',hue='cls', data=df_ex)
データの値によって色分けして表示したい。
そんな時は「seaborn」
x軸に表示したい項目名(x1),y軸に表示したい項目名(y1),
hueに分類を表す項目名(cls)を指定する,dataにはデータフレーム名(df_ex)を指定する。
するとhueに指定した項目の値に応じてデータの色を変えてくれる。
(7)plt.scatter(x軸,y軸, s=マーカーの大きさ, c=色,marker=マーカーの種類, alpha=透過性)
散布図では、x軸、y軸、マーカーの大きさ、色、マーカーの種類、透過性(0~1)を指定する。
例)plt.scatter(new_data0["開催回"],new_data0["第1数字"], s=50, c="blue",marker="D", alpha=0.5)
(8)データフレーム名.to_csv(csvファイル名,encoding=文字コード,index=False,column=False)
指定したデータフレームのデータを、文字コードや列名行名の表示有無(表示するしない場合は項目=Falseを指定)を指定してcsvファイルに保存する。
csvファイルに保存する。
例)new_df2.to_csv("file1.csv",encoding="cp932",index=False)
5.ソース
import pandas as pd
import datetime as dt
import seaborn as sns
#グラフを表示するライブラリ
import matplotlib.pyplot as plt
#日本語化のライブラリ
import japanize_matplotlib
#文字コードを指定して読み込む
df = pd.read_csv("loto6_2.csv",encoding="sjis")
row=df.shape[0]
#読み込んだcsvファイルの内容を表示
print(df)
開催回 日付 第1数字 第2数字 第3数字 第4数字 第5数字 第6数字 BONUS数字
0 1 2000/10/5 2 8 10 13 27 30 39
1 2 2000/10/12 1 9 16 20 21 43 5
2 3 2000/10/19 1 5 15 31 36 38 13
3 4 2000/10/26 16 18 26 27 34 40 13
4 5 2000/11/2 9 15 21 23 27 28 43
... ... ... ... ... ... ... ... ... ...
1651 1652 2022/1/6 8 15 16 23 38 43 2
1652 1653 2022/1/10 2 7 10 12 29 36 6
1653 1654 2022/1/13 9 10 14 21 22 33 26
1654 1655 2022/1/17 21 23 31 38 42 43 40
1655 1656 2022/1/20 11 12 14 28 36 38 37
[1656 rows x 9 columns]
#全データ数を表示
print(row)
print("nstart(集計開始回)")
nstart=input()
print("nend(カウント集計終了回)")
nend=input()
new_data=df[['開催回','第1数字','第2数字','第3数字','第4数字','第5数字','第6数字']]
1656
nstart(集計開始回)
100
nend(カウント集計終了回)
150
def drow_loto6graph(nstart0,new_data0,n_print0):
plt.ylim([1,43])
plt.xlim([int(nstart0),int(nstart0)+n_print0-1])
plt.grid(True)
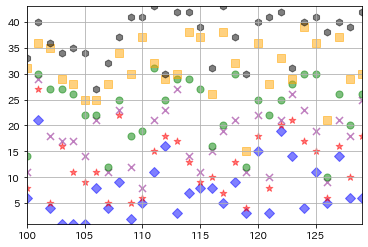
plt.scatter(new_data0["開催回"],new_data0["第1数字"], s=50, c="blue",marker="D", alpha=0.5)
plt.scatter(new_data0["開催回"],new_data0["第2数字"], s=50, c="red",marker="*", alpha=0.5)
plt.scatter(new_data0["開催回"],new_data0["第3数字"], s=50, c="purple",marker="x", alpha=0.5)
plt.scatter(new_data0["開催回"],new_data0["第4数字"], s=50, c="green",marker="o", alpha=0.5)
plt.scatter(new_data0["開催回"],new_data0["第5数字"], s=50, c="orange",marker="s", alpha=0.5)
plt.scatter(new_data0["開催回"],new_data0["第6数字"], s=50, c="black",marker="h", alpha=0.5)
plt.show()
#6つの当選数字から、2つの数字の連想配列を作成
def make_dictpare(new_data0):
print(new_data0.shape[0])
row0=new_data0.shape[0]
dict_graph={}
#数字の組み合わせと組み合わせの存在数の連想配列を作成
for i in range(0,row0):
for j in range(1,6):
for k in range(j+1,7):
key1=str(new_data0.iloc[i,j])+","+str(new_data0.iloc[i,k])
if key1 in dict_graph:
dict_graph[key1]=int(dict_graph[key1])+1
else:
dict_graph[key1]=1
return dict_graph
#print(dict_graph)
#組み合わせ数字の連想配列のデータのグラフ化
def make_paregraph(dict0,nstart0,nend0):
#空のデータフレーム作成
new_df2=pd.DataFrame()
keys0=dict0.keys()
#カウント数を入れる配列
list_val=[]
for k in keys0:
val0=dict0[k]
if not val0 in list_val:
list_val.append(val0)
min1=min(list_val)
max1=max(list_val)
print(list_val)
row1=0
for k in keys0:
splitstr=k.split(',')
col1=0
val=dict0[k]
#カウント数で3種類に分ける
if val<= int((min1+max1)/2):
class1="C"
elif val>int((min1+max1)/2) and val< int(3*(min1+max1)/4):
class1="B"
else:
class1="A"
if class1=="A" or class1 == "B":
tmpnum = pd.Series([splitstr[0], splitstr[1],str(val),class1],index=['数字1','数字2','カウント数','分類'])
new_df2=new_df2.append(tmpnum,ignore_index=True)
row1=row1+1
print(new_df2)
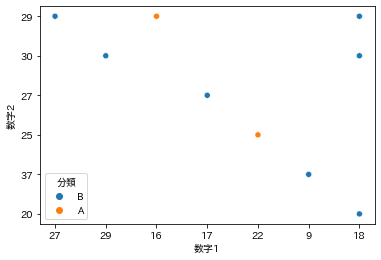
sns.scatterplot(x='数字1', y='数字2', hue='分類', data=new_df2)
csvfile="loto6pare_from"+str(nstart0)+"_to"+str(nend0)+".csv"
print(csvfile)
new_df2.to_csv(csvfile,encoding="cp932",index=False)
if nstart.isdecimal()==True and nend.isdecimal()==True:
#6つの当選数字を表示するデータ数
n_print=30
#開始が0より大きくrow未満かつ開始が終了未満、終了がrow以下
if int(nstart)>0 and int(nstart) < row and int(nstart)<int(nend) and int(nend) <= row:
#開始と終了の間隔が30未満のとき
if int(nstart)+n_print>int(nend):
new_data2=new_data[int(nstart)-1:int(nend)]
n_print1=int(nend)-int(nstart)
drow_loto6graph(nstart,new_data2,n_print1)
else:
new_data2=new_data[int(nstart)-1:int(nstart)+n_print-1]
drow_loto6graph(nstart,new_data2,n_print)
print(new_data2)
new_data3=new_data[int(nstart)-1:int(nend)]
print(new_data3)
dict_pare1=make_dictpare(new_data3)
make_paregraph(dict_pare1,nstart,nend)
else:
print("nstartは1以上"+str(row)+"未満で、nendはnstartより大きく"+str(row)+"以下で指定")
else:
print("nstart、nendは数値を指定")
開催回 第1数字 第2数字 第3数字 第4数字 第5数字 第6数字
99 100 6 8 11 14 31 33
100 101 21 27 29 30 36 40
101 102 4 5 18 27 35 36
102 103 1 16 17 27 29 34
103 104 1 11 17 26 28 35
104 105 1 9 14 22 25 34
105 106 8 11 21 22 25 27
106 107 4 5 11 12 28 32
107 108 9 22 23 25 34 37
108 109 2 5 12 18 30 41
109 110 5 6 8 19 37 41
110 111 11 15 21 31 32 43
111 112 16 18 23 25 29 30
112 113 3 17 27 29 30 42
113 114 7 13 14 29 38 42
114 115 8 9 11 27 37 39
115 116 8 10 15 16 26 31
116 117 5 7 19 20 38 43
117 118 9 13 21 30 32 37
118 119 3 4 11 12 15 30
119 120 15 18 22 25 36 40
120 121 3 8 10 22 28 41
121 122 19 20 21 25 33 42
122 123 14 21 26 28 29 31
123 124 4 17 23 30 39 40
124 125 11 15 19 30 36 41
125 126 5 6 9 10 21 38
126 127 14 16 21 26 37 40
127 128 6 10 18 20 29 39
128 129 6 18 25 26 30 42
開催回 第1数字 第2数字 第3数字 第4数字 第5数字 第6数字
99 100 6 8 11 14 31 33
100 101 21 27 29 30 36 40
101 102 4 5 18 27 35 36
102 103 1 16 17 27 29 34
103 104 1 11 17 26 28 35
104 105 1 9 14 22 25 34
... ... ... ... ... ... ... ... ... ...
146 147 16 18 20 29 30 38
147 148 3 16 18 20 28 29
148 149 8 9 13 20 33 37
149 150 10 11 18 20 31 43
51
[2, 1, 3, 4, 6, 5]
数字1 数字2 カウント数 分類
0 27 29 4 B
1 29 30 4 B
2 16 29 6 A
3 17 27 4 B
4 22 25 5 A
5 9 37 4 B
6 18 30 4 B
7 18 29 4 B
8 18 20 4 B
loto6pare_from100_to150.csv
6.参考サイト
KYO's LOTO
当選番号データだけではなく、各数字の出現回数など様々なデータを収集されています。
7.最後に
30回分の当選数字データでは、満遍なく数字が出ていて傾向
がつかみにくい。
カウント数散布図で、Aランクで表示されている点は、他の
組み合わせより当選回数が多かったことは確かである。
だが、その組み合わせが次回の当選ナンバーに含まれるかは神のみぞ知るところである。