データ分析をはじめるとき、データの平均や分散などの要約統計量を確認するかと思います。
しかし、要約統計量を確認するだけでは不十分な場合があります。
import pandas as pd
import seaborn as sns
# データの読み込み
df = pd.read_csv('https://git.io/vD7ui')
# 散布図
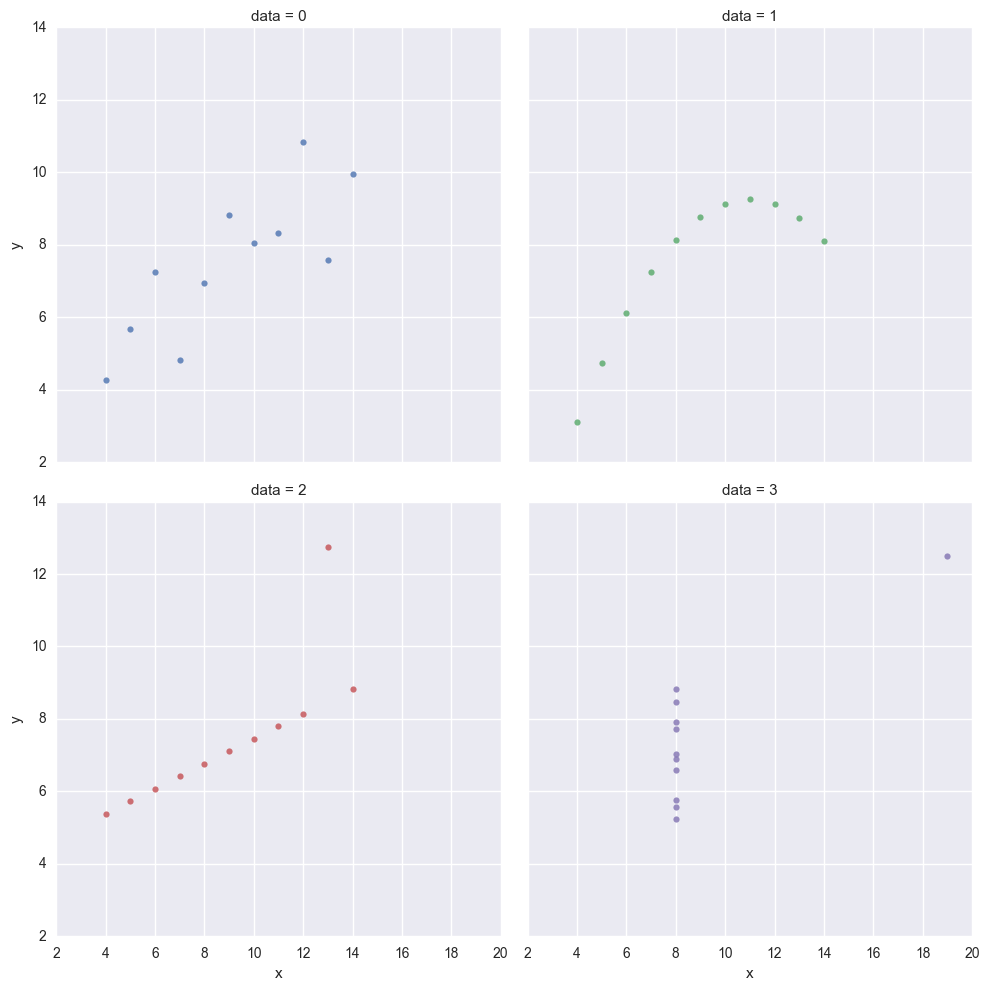
sns.lmplot(x='x', y='y', col='data', hue='data', col_wrap=2, fit_reg=False, data=df)
と、散布図を見ると、異なったデータであることが分かりますが、平均と標準偏差は同じ値をとります。
# 平均
df.groupby('data').mean()
| data | x | y |
|---|---|---|
| 0 | 9 | 7.500909 |
| 1 | 9 | 7.500909 |
| 2 | 9 | 7.500000 |
| 3 | 9 | 7.500909 |
# 標準偏差
df.groupby('data').std()
| data | x | y |
|---|---|---|
| 0 | 3.316625 | 2.031568 |
| 1 | 3.316625 | 2.031657 |
| 2 | 3.316625 | 2.030424 |
| 3 | 3.316625 | 2.030579 |
細かい値は異なりますが、ほとんど同じ値であることが分かります。
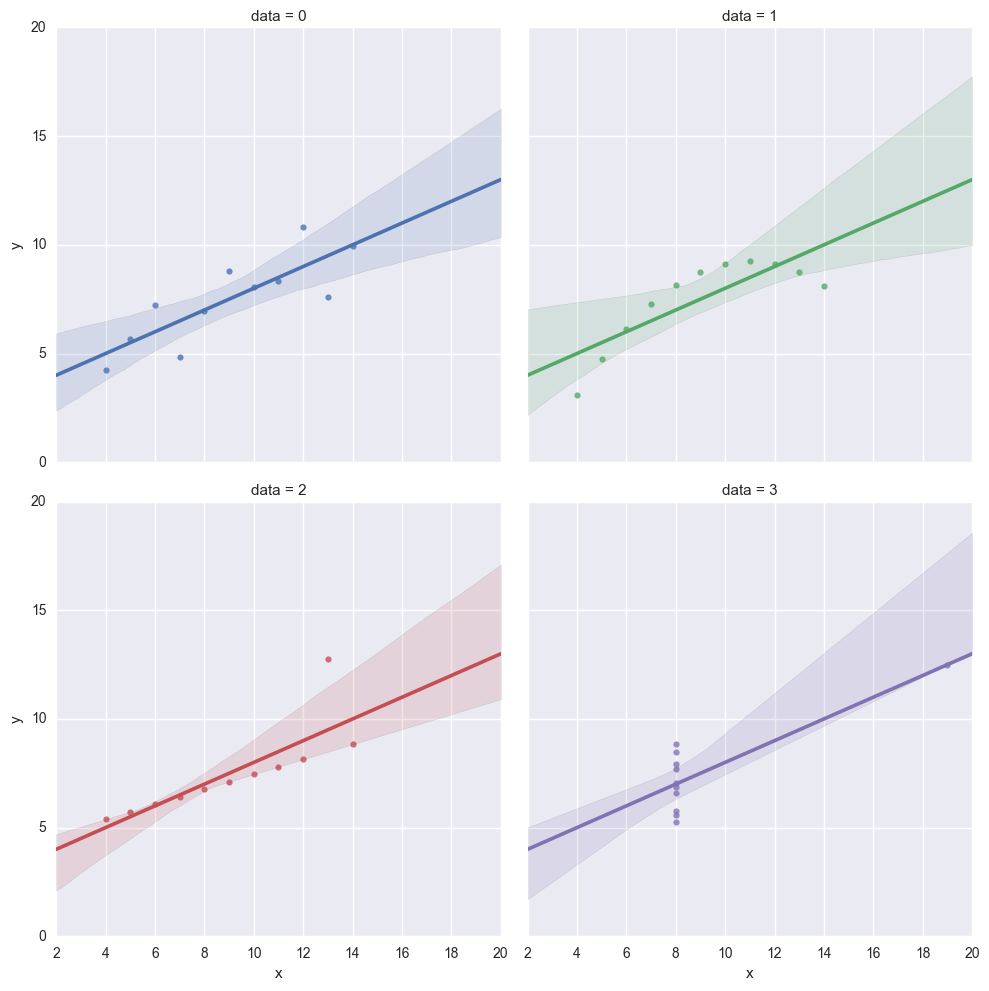
また、回帰直線も全く同じ直線になります。
# 散布図 + 回帰直線
sns.lmplot(x='x', y='y', col='data', hue='data', col_wrap=2, fit_reg=True, data=df)
pandasでは、describeメソッドでまとめて要約統計量を表示することができます。
# 要約統計量
df.groupby('data').describe()
x y
data
0 count 11.000000 11.000000
mean 9.000000 7.500909
std 3.316625 2.031568
min 4.000000 4.260000
25% 6.500000 6.315000
50% 9.000000 7.580000
75% 11.500000 8.570000
max 14.000000 10.840000
1 count 11.000000 11.000000
mean 9.000000 7.500909
std 3.316625 2.031657
min 4.000000 3.100000
25% 6.500000 6.695000
50% 9.000000 8.140000
75% 11.500000 8.950000
max 14.000000 9.260000
2 count 11.000000 11.000000
mean 9.000000 7.500000
std 3.316625 2.030424
min 4.000000 5.390000
25% 6.500000 6.250000
50% 9.000000 7.110000
75% 11.500000 7.980000
max 14.000000 12.740000
3 count 11.000000 11.000000
mean 9.000000 7.500909
std 3.316625 2.030579
min 8.000000 5.250000
25% 8.000000 6.170000
50% 8.000000 7.040000
75% 8.000000 8.190000
max 19.000000 12.500000
平均と標準偏差はさきほど、見たとおりですが、四分位点は若干異なることがわかります。特にdata3は大きく異なります。
このように、散布図は異なるが、統計量や回帰直線が同じになるデータをアンスコムの例といいます。なので、統計量だけでなく、散布図を描くことが重要になってきます。
ただ、現実のデータにおいて、二次元であることは少ないかと思います。その場合、主成分分析(PCA)を用いて次元を2次元まで落として可視化するなど工夫が必要です。
-
data列が同じ値の行が同じデータを表します ↩