「統計WEB Step1. 基礎編」のまとめ
※高校数学の内容は一部省略する。
16. 標本と抽出法
母集団と標本
- 母集団
調査や研究の対象となるものの全体。 - 標本
母集団の情報を推測するために、母集団から選ばれた一部の集団 - 抽出
母集団から一部を選んで標本とすること - 推測統計学
標本を用いて、母集団の性質を推測すること - 記述統計学
取得した手元のデータ(母集団・標本問わず)を用いて、データの特徴をグラフや表などを用いて分かりやすく表現すること
有限母集団修正
標本を抽出するたびに母集団のデータがどんどん減ってしまうため、推定値に偏りが出てしまう可能性がある。
そこで平均値の分散を求める場合、$\frac{N-n}{N-1}$をかけて「有限母集団修正」を行う。
(N:母集団の大きさ。 n:抽出するデータの数)
$N→\infty$の場合、$\frac{N-n}{N-1}=1$になる。
この時、有限母集団における平均値の分散 = 無限母集団における平均値の分散
※有限母集団:母集団の数が有限であること
全数調査と標本調査
- 全数調査
調査対象となる母集団を全て調べること。(例:国勢調査) - 標本調査
調査対象となる母集団の一部を取り出して調べること。(例:アンケート)
標本調査
母集団からできるだけ偏りがないように調査対象を抽出しなければならない。
- 単純無作為抽出法
母集団から、「完全に」「ランダムに」必要数だけサンプルを抽出する方法。 - 復元抽出法
一度抽出された標本を母集団の中に戻す抽出方法。
(調査対象が重複する可能性あり。) - 非復元抽出法
一度抽出された標本は母集団の中に戻さない抽出方法。
(調査対象は重複しない。)
標本の抽出方法
母集団から完全に無作為に調査対象を取り出すのは難しいため、無作為抽出法が用いられる。
層化抽出法(層別抽出法)
母集団をあらかじめいくつかの層(グループ)に分けておき、各層の中から必要な数の調査対象を無作為に抽出する方法。
(例:母集団の男女比と標本の男女比を揃えるように、男女それぞれから抽出する)
- メリット
- 母集団内情報(年齢別、性別など)の比較を行える
- 推定精度が高くなる
- 各層において分布が大きく異なる場合に使える
- デメリット
- 母集団の構成情報を事前に知っておく必要がある
クラスター抽出法(集落抽出法)
①母集団を、小集団である「クラスター(集落)」に分ける
②分けられたクラスターの中から、いくつかのクラスターを無作為抽出する
③それぞれのクラスターにおいて全数調査を行う
(例:高校生の平均身長を調査する際、高校を1つのクラスターとしてランダムに10校を選んでから、その10校に通う高校生全員の身長を測定する)
- メリット
- クラスターの情報(高校名など)さえあれば抽出することができるので、時間や手間を節約できる
- デメリット
- 同じクラスターに属する調査対象は似た性質を持ちやすいため、標本に偏りが生じる可能性あり
多段抽出法
母集団をいくつかのグループに分け、そこから無作為抽出でいくつかグループを選び、さらにその中から無作為抽出でいくつかのグループを選び…という操作を繰り返して、最終的に選ばれたグループの中から調査対象を無作為抽出する方法
(例:全国から市区町村を●個無作為抽出
→市区町村から地区を■個無作為抽出
→区の中からそれぞれ△人を無作為抽出)
- メリット
- コストを低く抑えられる
- 抽出効率が高い
- デメリット
- サンプルサイズが小さい場合、標本に偏りが生じる可能性あり
系統抽出法
通し番号をつけた名簿を作成し、1番目の調査対象を無作為に選び、2番目以降の調査対象を一定の間隔で抽出する方法
(例:ランダムに選ばれた番号から3人おきに(3番おきに)人を抽出していく)
- メリット
- 単純無作為抽出より手間や時間やコストが掛からない
- デメリット
- 名簿の並び順に何らかの周期があると標本に偏りが生じる可能性あり
二相抽出法
層化抽出を行いたいが母集団の情報がない場合、まず母集団から標本を抽出して母集団の情報を取得し(第一相)、
その情報をもとに層化抽出を行う方法(第二相)
(例)男女比が分からないある都市の住民に対してアンケート調査を行う場合、まず住民の中から●人を抽出して男女比を調べ、男女比を揃えた状態でそれぞれ無作為に抽出する。
- メリット
- 母集団の情報がない場合、効率よく層化抽出を行える
- デメリット
- 抽出するサンプルサイズが小さい場合、標本に偏りが生じる可能性あり
研究デザイン
実験研究
研究対象に対して何らかの介入(薬を飲んでもらったり、治療を受けてもらったりなど)を行い、その効果を評価する研究。
ランダム化比較試験(RCT:Randomized Controlled Trial)(前向き研究)
実験群と対照群への割り付けをランダムに行い、介入の効果を調べる研究。
(例)薬の効果検証のため、参加者からA薬投与群と、そうでないプラセボ投与群に分けて試験する。
クロスオーバー試験(前向き研究)
①対象者を実験群、対象群の2群に分けて介入を行い、比較を行う。
②一定の期間をあけてから実験群の対照群を入れ替えて再度介入を行い、比較を行う。
(例)薬の効果検証のため、参加者からA薬投与群と、そうでないプラセボ投与群に分けて試験する。休止期間後、グループを入れ替えてA薬投与・プラセボ投与を行う。
- メリット
- 少ないサンプルサイズでも実施できる
- デメリット
- 休止期間前の効果が残ったまま(持ち越し効果)になる可能性あり
観察研究
研究対象の観察によってデータを集めて解析を行う非実験的研究。(アンケートなど)
横断研究
ある1時点において断面的調査を行い、要因と結果の関連を調べる研究。
過去に遡った調査や、未来に向かって調査を行わない。
例)年齢と視力について興味がある場合、さまざまな年齢の人に対して視力検査を行う。
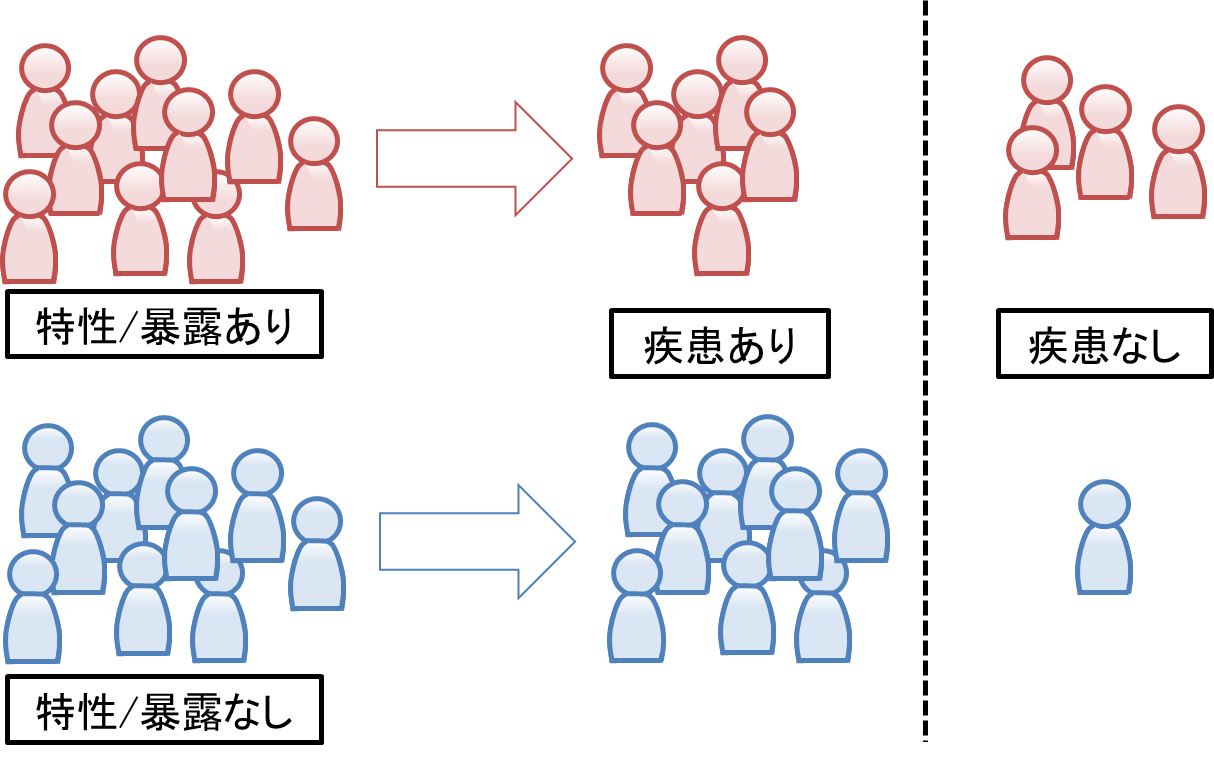
コホート研究(前向き研究/後ろ向き研究)
異なる特性を持つ対象集団(コホート)において、ある特性を持つ/暴露がある群とそうではない群に分け、時間の流れに沿って疾患の発生や改善などを観察し、その特性/暴露と疾患との関係を調べる研究。
(例)注意障害有無群で、1年後に転倒経験有無に関連があるか調べる
画像参照:16-4. 研究デザイン
https://bellcurve.jp/statistics/course/18127.html
ケースコントロール研究(症例対照研究)(後ろ向き研究)
ある病気に罹患している群とそうでない対照群に対して、その病気の特性/暴露の有無との関係を調べる研究。発生頻度が稀な病気の研究に対して広く使われる。
(例)乳がんの患者と健常者との間で、ある遺伝子への変異発生頻度を比較する
画像参照:16-4. 研究デザイン
https://bellcurve.jp/statistics/course/18127.html
17. 大数の法則と中心極限定理
母集団から無作為に標本を選んできてその平均値を求めることを繰り返しても、標本の平均(=標本平均)は毎回ぴったりと母集団の平均(=母平均)に一致するとは限らない。
大数の法則
確率pで起こる事象において、試行回数を増やすほど、その事象が実際に起こる確率はpに近づくこと。
⇒母平均が$\mu$である集団から標本を抽出する場合、サンプルサイズ(=標本の大きさ)が大きくなるにつれて、標本平均は母平均$\mu$に近づく
中心極限定理
母集団分布に関係なく、抽出するサンプルサイズnが大きくなるにつれて正規分布$N(\mu,\frac{\sigma^2}{n})$に収束すること。
($\mu$:母平均。 $\sigma^2$:分散)
また、標準化を行うと以下のようになる。
\displaylines{
z=\frac{\bar{x}-\mu}{\sqrt{\frac{\sigma^2}{n}}}
=\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}}
}
18. 母平均の点推定
- 推定
母集団を特徴づける母数(パラメーター:平均など)を統計学的に推測すること。 - 検定
母集団から抽出された標本の統計量に関する仮説が正しいかを統計学的に判定すること。
(例)日本人全員(母集団)からランダムに100人を抽出した標本について
- 推定
抽出された100人の身長から日本人全員の平均身長を推測すること。 - 検定
抽出された100人の平均身長と日本人の平均身長から、100人の平均値は妥当かどうかを判定すること。
推定の種類
- 点推定:平均値などを1つの値で推定すること。
- 区間推定:平均値などをある区間でもって推定すること。
母平均の点推定と推定量・推定値
点推定
母集団から抽出された標本を用いて母集団を特徴づけるパラメータ(母数)を推測すること。
(例)47都道府県にある映画館の合計スクリーン数の点推定について
抽出した10都道府県の全スクリーン数を割り出す。
⇒この平均値$\hat{\mu}$を47都道府県(=母集団)の平均値(母平均$\mu$)と見なしてしまう
※この平均値は推定値とも呼べる
⇒母平均の点推定
推定量
パラメータを推定するために利用する数値の計算方法や計算式。
n回の試行によって得られた値$x_i(i=1,2,\cdots)$の平均を計算する場合。
\displaylines{
\bar{x}=\frac{1}{n}\sum_{i=1}^n x_i
}
推定量の性質
- 一致性
サンプルサイズnが大きくなれば、推定量がだんだんと真のパラメータに近づく性質。 - 不偏性
推定量の期待値がパラメータに一致する必要がある。
サンプルサイズnが小さい時も大きい時も、推定量の外れ具合が偏っていない。
推定値
実際に試行を行った結果から計算した値
標本平均の性質
標本平均は一致推定量であり不偏推定量である。
そのため、標本平均の値を母平均の推定量として使うことができる。
標本分散と不偏分散
母分散を$\sigma^2$ 、標本分散を$S^2$ 、不偏分散を$s^2$と表す。
標本分散 (一致性○、不偏性×)
nが十分に大きくない場合、標本分散の期待値は母分散に一致せず、母分散より小さくなる。
データの平均を$\bar{x}$ 、個々のデータを$x_i(i=1,2,\cdots)$、サンプルサイズをnとすると
\displaylines{
S^2=\frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^2
}
不偏分散 (一致性○、不偏性○)
標本分散の期待値が母分散に一致するように標本分散の算出式にn/(n-1)をかけたもの。
\displaylines{
s^2=\frac{n}{n-1} \times \frac{1}{n}\sum_{i=1}^n (x_i-\bar{x})^2
=\frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})^2
}
標準偏差と標準誤差
標準偏差
母集団から得られた個々のデータのばらつきを表すものであり、分散の正の平方根で求められる。
\displaylines{
s=\sqrt{\frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})^2}
}
標準誤差SE
標本平均の標準偏差。
推定量の標準偏差であり、標本から得られる推定量そのもののバラつき(=精度)を表す。
中心極限定理より、
平均$\mu$、分散$\sigma^2$の母集団のサンプルサイズnが大きくなるにつれて正規分布$N(\mu,\frac{\sigma^2}{n})$に収束する。
この時、標本平均の標準偏差は$\sqrt{\frac{\sigma^2}{n}}=\frac{\sigma}{\sqrt{n}}$に近づく。
標本の分散は母分散$\sigma^2$ではなく不偏分散$s^2$を用いる。
\displaylines{
SE=\frac{s}{\sqrt{n}}
=\frac{\sqrt{\frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})^2}}{\sqrt{n}}
}
19. 母平均の区間推定(母分散既知)
区間推定とは
母集団の従う分布が正規分布であると仮定できるときに、標本から得られた値を使ってある区間(信頼区間)でもって母平均などを推定する方法。
- 信頼区間
区間推定において、ある確率(信頼係数)のもとで母数がその内に含まれると推定された区間のこと。
信頼区間の求め方
- 母分散が分かっている場合(母分散既知)
母分散$\sigma^2$の値を使い、標準正規分布を用いて信頼区間を算出する - 母分散が分からない場合(母分散未知)
次の式から算出される不偏分散$s^2$の値を使い、t分布を用いて信頼区間を算出する(20章参照)
\displaylines{
s^2=\frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})^2
}
※母平均の区間推定では「95%信頼区間(95%CI)」を求めることが多い
⇒母集団から抽出した標本の標本平均から母平均の95%信頼区間を求める、
という作業を100回やったときに、95回はその区間の中に母平均が含まれる
- 信頼係数(信頼度)
「○%信頼区間」に入る、95%や99%、90%のような、ある区間に母数が含まれる確率のこと
母平均の信頼区間の求め方(母分散既知)
(例)各都道府県内にある映画館のスクリーンの合計数の区間推定
無作為に10都道府県のデータを抽出する。
スクリーン数の分布は正規分布に従うものとする。
母分散(47都道府県にある映画館の合計スクリーン数の分散)は$\sigma^2$=5560とする。
このデータから「母平均の95%信頼区間」を求める。
①10都道府県の標本平均$\bar{x}$を求める
②中心極限定理より、標本平均の標準化を行う
($\mu$:母平均。 $\sigma^2$:分散。n:サンプルサイズ)
また、標準化を行うと以下のようになる。
\displaylines{
z=\frac{\bar{x}-\mu}{\sqrt{\frac{\sigma^2}{n}}}
}
③②で標準化した値が標準正規分布の95%の面積(=確率)の範囲にあればよい
(=両端の2.5%の面積の部分の極端な範囲に入らなければよい)ので、
標準正規分布表から上側2.5%点zを調べる
画像参照:19-2. 母平均の信頼区間の求め方(母分散既知)
https://bellcurve.jp/statistics/course/8888.html
標準正規分布表より、
\displaylines{
-1.96 \leq \frac{\bar{x}-\mu}{\sqrt{\frac{\sigma^2}{n}}} \leq 1.96
}
④95%信頼区間を求める
③の式を変形する。
\displaylines{
\bar{x}-1.96 \times \sqrt{\frac{\sigma^2}{n}} \leq \mu \leq
\bar{x}+1.96 \times \sqrt{\frac{\sigma^2}{n}}
}
$\bar{x}$=①で求めた標本平均、$\sigma^2$=5560なので、$\mu$の範囲が求められる。
パーセント点
- 上側☆%点(パーセント点)
ある確率分布関数において、ある値▲より大きくなる確率が☆%であるとき、この▲のこと - 上側確率
ある値▲より大きくなる確率のこと(下側確率はその逆の意味)
画像参照:19-2. 母平均の信頼区間の求め方(母分散既知)
https://bellcurve.jp/statistics/course/8888.html
95%信頼区間のもつ意味
95%信頼区間:
「母集団から標本を取ってきて、その平均から95%信頼区間を求める、という作業を100回やったときに、95回はその区間の中に母平均が含まれる」という"頻度"もしくは"割合"を意味する。
信用区間
ベイズ統計学における区間推定で使われるもの。
95%信用区間:
「母平均が95%の確率で推定された信用区間に含まれる」という意味。
さまざまな信頼区間(母分散既知)
- 信頼係数(○%)が大きいほど、信頼区間の幅(△$\leq \mu \leq $■)は広くなる
- サンプルサイズnが大きいほど、信頼区間の幅は狭くなる
20. 母平均の区間推定(母分散未知)
母分散$\sigma^2$が分からない場合の、母平均の区間推定を行う。
標本とt分布
母分散$\sigma^2$が分からない場合、不偏分散$s^2$を使う。
標準正規分布ではなく「t分布」を使う。
- t分布
正規分布は定義の中で母数を用いるのに対して、t分布は不偏推定量を用いる。
自由度が大きくなるにつれて、標準正規分布に近づく。 - 自由度(df)
ある変数において自由な値をとることのできるデータの数。
\displaylines{
z=\frac{\bar{x}-\mu}{\sqrt{\frac{s^2}{n}}}
}
t分布の性質
t分布の成り立ち
標準正規分布N(0, 1)に従うZと自由度nのカイ二乗分布Wがあり、これらが互いに独立であるとき、次の式から算出されるtは自由度nのt分布に従う。
\displaylines{
z=\frac{Z}{\sqrt{\frac{W}{n}}}
}
正規分布$N(\mu,\sigma^2)$に従う母集団から抽出した、サンプルサイズnの標本($x_1,x_2,\cdots ,x_n$)を考える。
このとき、$z=\frac{\bar{x}-\mu}{\sqrt{\frac{\sigma^2}{n}}}$は標準正規分布N(0, 1)に、$\sum_{i=1}^n \frac{(x_i-\bar{x})^2}{\sigma^2}$は自由度(n-1)のカイ二乗分布に従う。
このとき、tは自由度(n-1)のt分布に従う。
期待値と分散
確率変数Xが自由度mのt分布に従っている時、Xの期待値と分散は以下のようになる。
\displaylines{
E(X) = 0 (m>1)\\
V(X) = \frac{m}{m-2} (m>2)
}
t分布表
自由度$\upsilon$のt分布において、水色部分の面積が$\alpha$となるtの値$t_\alpha(\upsilon)$を表す。
(例)自由度5で、95%信頼区間を求める場合、$t_{0.025}(5)$を求める。
画像参照:20-2. t分布表
https://bellcurve.jp/statistics/course/8970.html
| 上側確率$\alpha$ | ||||
| 0.1 | 0.05 | 0.025 | ||
| 自由度$\upsilon$ | 1 | |||
| 2 | ||||
| ... | ||||
| 5 | ||||
サンプルサイズが大きい時
- サンプルサイズが30以上であれば、ほぼ正規分布になる
- t分布の自由度が大きくなるにつれて標準正規分布に近づく
母平均の信頼区間の求め方(母分散未知)
(例)ある工場で、生産している部品Aを1時間毎にランダムに1つ抜き取り、その重さを検査する。計10個の部品Aの重さを測定した結果は下表とする。
母分散(すべての部品Aの重さから算出した分散)は分かっていない。
また、部品Aの重さは正規分布に従うものとする。
このデータから「母平均の95%信頼区間」を求める。
| No. | 部品Aの重さ (g) |
|---|---|
| 1 | 100.2 |
| 2 | 101.5 |
| 3 | 98.0 |
| 4 | 100.1 |
| 5 | 100.9 |
| 6 | 99.6 |
| 7 | 98.6 |
| 8 | 102.1 |
| 9 | 101.4 |
| 10 | 97.9 |
①標本平均$\bar{x}$と不偏分散$s^2$を求める
\displaylines{
\bar{x}=100.3\\
s^2 =\frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})^2=2.22
}
②統計量tを計算する
中心極限定理より、分散の代わりに不偏分散を使って標準化を行う
($\mu$:母平均。 $s^2$:不偏分散。n:サンプルサイズ)
\displaylines{
t=\frac{\bar{x}-\mu}{\sqrt{\frac{s^2}{n}}}
}
③②で算出された統計量tがt分布の95%の面積(=確率)の範囲にあればよい(=両端の2.5%の面積の部分の極端な範囲に入らなければよい)ので、t分布表から上側2.5%点を調べる(自由度はn-1=10-1=9で探す!)
t分布表より、
\displaylines{
-2.262 \leq \frac{\bar{x}-\mu}{\sqrt{\frac{s^2}{n}}} \leq 2.262
}
④95%信頼区間を求める
③の式を変形する。
\displaylines{
\bar{x}-2.262 \times \sqrt{\frac{s^2}{n}} \leq \mu \leq
\bar{x}+2.262 \times \sqrt{\frac{s^2}{n}}
}
$\bar{x}$=①で求めた標本平均、$s^2$=①で求めた不偏分散なので、$\mu$の範囲が求められる。
さまざまな信頼区間(母分散未知)
- 信頼係数(○%)が大きいほど、信頼区間の幅(△$\leq \mu \leq $■)は広くなる
- サンプルサイズnが大きいほど、区間は狭くなる
21. 母比率の区間推定
母比率の信頼区間の求め方
二項分布より、成功確率pの試行をn回行うときに成功する回数をXとすると、Xは二項分布B(n,p)に従う。
この時の期待値と分散は以下のようになる。
\displaylines{
期待値E(X)=np\\
分散V(X)=np(1-p)
}
Xを標準化した値Zはnが十分に大きいときには標準正規分布N(0,1)に従う。
\displaylines{
Z=\frac{X-np}{\sqrt{np(1-p)}}
}
標本比率
$\hat{p}=\frac{X}{n}$
成功回数を試行回数で割ったもの。
pの一致推定量であり、nが大きい時ほぼpに一致する。
これを標準化の式に当てはめると
\displaylines{
Z=\frac{X-np}{\sqrt{np(1-p)}}
=\frac{\frac{1}{n}}{\frac{1}{n}} \times \frac{X-np}{\sqrt{np(1-p)}}
=\frac{\frac{X}{n}-p}{\sqrt{\frac{p(1-p)}{n}}} \\
=\frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}
}
$\hat{p}$は近似的に正規分布$N(p,\frac{p(1-p)}{n})$に従う。
母比率の信頼区間
(例)標準正規分布表から読み取ったZの95%信頼区間
-信頼区間は-1.96≤Z≤1.96なので、
\displaylines{
-1.96 \leq \frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}} \leq 1.96
\\
\hat{p}-1.96 \times \sqrt{\frac{p(1-p)}{n}} \leq p \leq \hat{p}+1.96 \times \sqrt{\frac{p(1-p)}{n}}
}
$\hat{p}$はpの一致推定量であり、nが大きい時ほぼpに一致するので、pを$\hat{p}$に置き換えられる。
\displaylines{
\hat{p}-1.96 \times \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \leq p \leq \hat{p}+1.96 \times \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}
}
必要なサンプルサイズ
母比率の信頼区間の例より、
母比率pの95%信頼区間は、標本比率$\hat{p}$の両側に$1.96 \times \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}$ずつ幅を取ったものであると考えることができる。
つまり、95%信頼区間の幅は$2 \times 1.96 \times \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}$である。
推定量$\hat{p}$が分かれば、必要なサンプルサイズが分かる。
信頼係数$\alpha$(=100$\alpha$%)の場合には、正規分布の累積確率を用いて次のように表せる。
\displaylines{
2 \times z_{\frac{1-\alpha}{2}} \times \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}
}
母比率の信頼区間について次の3点が成り立つ
- nが大きくなると信頼区間の幅は狭くなり、より正確な推定ができる
(信頼区間の長さが$\sqrt{n}$に反比例しているため) - $\hat{p}$が0.5のとき、最も信頼区間が広くなり、0.5から外れるごとに信頼区間は狭くなる
($\hat{p}(1-\hat{p})$の部分が最大値を取るため) - 信頼区間の幅は$z_{\frac{1-\alpha}{2}}$に比例する
※Z:標準正規分布におけるx軸上の値。
$\alpha$:信頼係数(○%)
22. 母分散の区間推定
カイ二乗分布
$Z_1,Z_2,\cdots ,Z_k$が互いに独立で標準正規分布N(0,1)に従う確率変数であるとき、次の式から算出される自由度kの$\chi^2$(カイの二乗)が従う確率分布のこと。
※自由度≒データ数
\displaylines{
\chi^2 = Z_1^2+Z_2^2+\cdots +Z_k^2
}
自由度が1のとき$\chi^2 (1) = Z_1^2$になる。
カイ二乗分布はt分布と同様、自由度によって形が異なる分布。
自由度kのカイ二乗分布の確率密度関数は以下のようになる。
\displaylines{
f(x;k)= \left\{
\begin{array}{ll}
\frac{1}{2^{\frac{k}{2}} \Gamma(\frac{k}{2})} e^{-\frac{x}{2}} x^{\frac{k}{2}-1} & (x \geq 0) \\
0 & (x \lt 0)
\end{array}
\right.
}
カイ二乗分布の性質
期待値と分散
確率変数Xが自由度kのカイ二乗分布に従っている時
\displaylines{
期待値E(X)=k\\
分散V(X)=2k
}
再生性
2つの確率変数$X_1, X_2$がそれぞれ独立に自由度$k_1, k_2$のカイ二乗分布$\chi^2 (k_1), \chi^2 (k_2)$に従うとき、
$X_1+X_2$は自由度$k_1+k_2$のカイ二乗分布$\chi^2 (k_1+k_2)$に従う。
正規分布に従う母集団からの無作為標本
①確率変数$X_1,X_2,\cdots ,X_k$がそれぞれ独立に正規分布$N(\mu,\sigma^2)$に従うとき、以下は自由度kのカイ二乗分布$\chi^2 (k)$に従う。
\displaylines{
\sum_{i=1}^k(\frac{X_i-\mu}{\sigma})^2
}
②次の式の値は自由度k-1のカイ二乗分布$\chi^2 (k-1)$に従う
\displaylines{
\sum_{i=1}^k(\frac{X_i-\bar{X}}{\sigma})^2
=\frac{(k-1)S^2}{\sigma^2}
}
($\bar{X}$:標本平均。 $S^2$:不偏分散)
カイ二乗分布と指数分布の関係
自由度2のカイ二乗分布は$\lambda=\frac{1}{2}$の指数分布と一致する。
母分散の信頼区間の求め方
母分散の区間推定ではカイ二乗分布を使う。
母集団が母分散$\sigma^2$の正規分布に従う時、自由度n-1のカイ二乗分布に従う。
\displaylines{
\chi^2 = \frac{(n-1)s^2}{\sigma^2}
}
($\sigma^2$:母分散。 $s^2$:不偏分散。n:サンプルサイズ)
(例)あるデータの母分散の95%信頼区間を求める。
①サンプルサイズnの標本の不偏分散を求める
\displaylines{
s^2 =\frac{1}{n-1}\sum_{i=1}^n (x_i-\bar{x})^2
}
②使用するカイ二乗分布の自由度を決める
⇒n-1を用いる
③$\frac{(n-1)s^2}{\sigma^2}$がカイ二乗分布の95%の面積(=確率)の範囲にあればいい
⇒両端の2.5%の面積の部分の極端な範囲に入らなければいい
⇒カイ二乗分布表から自由度n-1における上側2.5%点と下側2.5%点(=上側97.5%点)をそれぞれ調べる