「統計WEB Step0. 初級編」のまとめ
※Step1. 基礎編と重複しそうなところは省略する
1. データの集計
データの種類
- 質的変数
性質を表すデータ。
(例)住所、血液型、好きな食べ物 - 量的変数
数値を表すデータ。- 離散変数
とびとびの値。(兄弟姉妹や鉛筆の数。1個2個、1人2人) - 連続変数
すき間なく連続した値。(身長、体重、気温)
- 離散変数
①質的変数の集計
(例)猫100匹のデータを使った毛色の集計。(集計表)
度数:それぞれのカテゴリの数
| 毛色 | 度数 |
|---|---|
| 白 | 27 |
| 黒 | 20 |
| 灰色 | 18 |
| オレンジ | 15 |
| 茶トラ | 10 |
| キジトラ | 7 |
| サビ | 3 |
| 合計 | 100 |
集計表を使ったグラフ
- 棒グラフ
- 円グラフ
- 帯グラフ
帯全体に対して、データの大きさを割合で表す。
(円グラフの帯バージョン)
②量的変数の集計
- 階級:度数を集計するための区間
- 階級値:階級の真ん中の値
- 度数:各階級に含まれるデータ数
- 相対度数:各階級の度数が全体に占める割合
- 累積相対度数:相対度数の累計
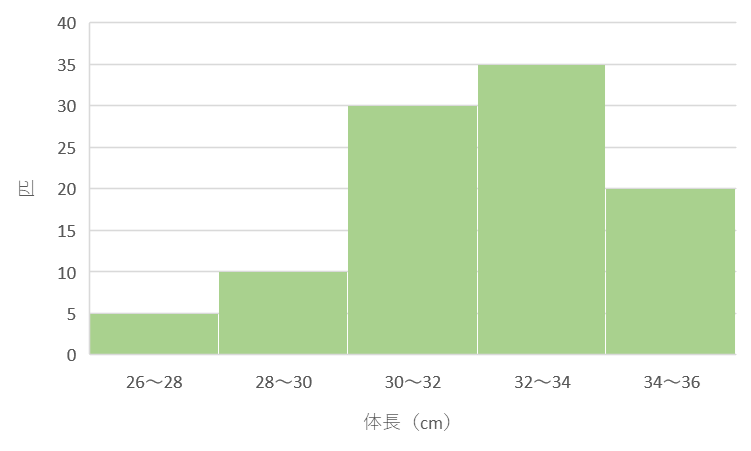
(例)猫100匹のデータを使った体長の集計。(度数分布表)
| 階級(cm以上~cm未満) | 階級値(cm) | 度数 | 相対度数 | 累積相対度数 |
|---|---|---|---|---|
| 26~28 | 27 | 5 | 5% | 5% |
| 28~30 | 29 | 10 | 10% | 15% |
| 30~32 | 31 | 30 | 30% | 45% |
| 32~34 | 33 | 35 | 35% | 80% |
| 34~36 | 35 | 20 | 20% | 100% |
度数分布表を使ったグラフ
- ヒストグラム
横軸:体長の階級
縦軸:度数
2. さまざまなグラフ
クロス集計表
2つのカテゴリに属するデータについて、各カテゴリで同時に分類し、その度数を集計したもの。
(例)猫100匹に対して持っていくおやつの集計表
| かつおぶし | にぼし | ささみ | チーズ | 合計 | |
|---|---|---|---|---|---|
| オス | 25 | 28 | 3 | 4 | 60 |
| メス | 20 | 12 | 7 | 1 | 40 |
| 合計 | 45 | 40 | 10 | 5 | 100 |
- かつおぶしを持っていきたいオスは25匹
- ささみを持っていきたい猫は全部で10匹
などが分かる。
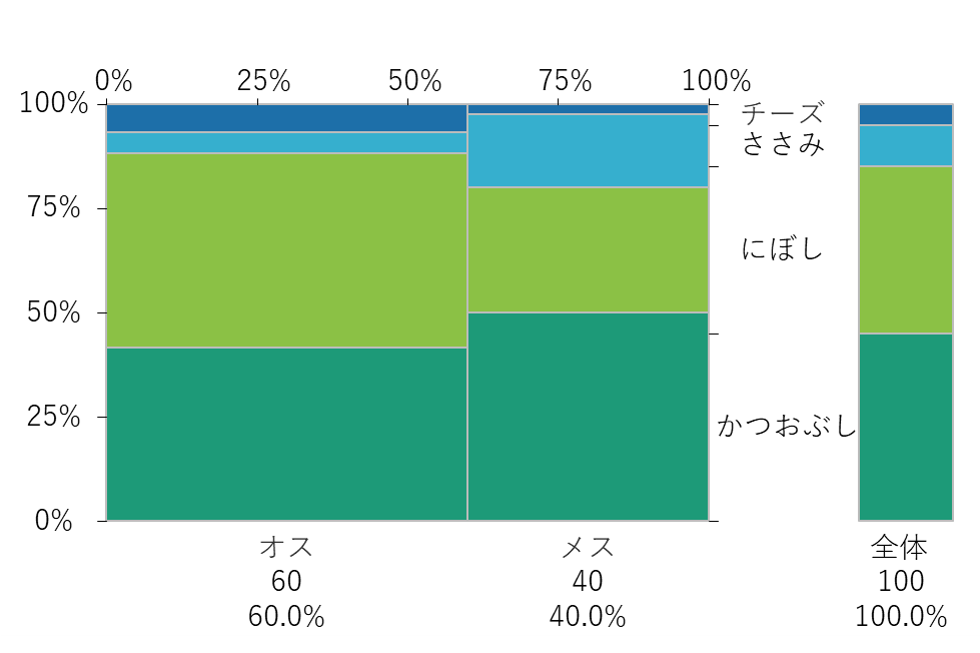
モザイク図
クロス集計表の各層を縦棒の積み上げ棒グラフとして表したグラフ
画像参照:2-2. モザイク図を描いてみよう
https://bellcurve.jp/statistics/course/18862.html
グラフより、
- 性別の割合は、オス:メス=60:40なので、横幅の比は3:2になっている
- 性別ごとのおやつの割合は、縦棒の積み上げ棒グラフとして表している
- オス場合、高さの比はかつおぶし:にぼし:ささみ:チーズ=0.42:0.46:0.05:0.07
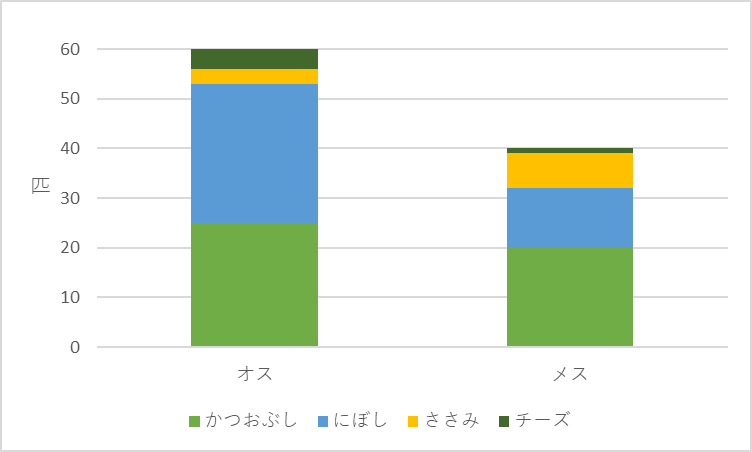
積み上げ棒グラフ
棒の高さが合計度数になる棒グラフ。
合計の内、各カテゴリの度数をある程度把握できる。
3. 時系列データ
時間の経過に従って測定されたデータ。
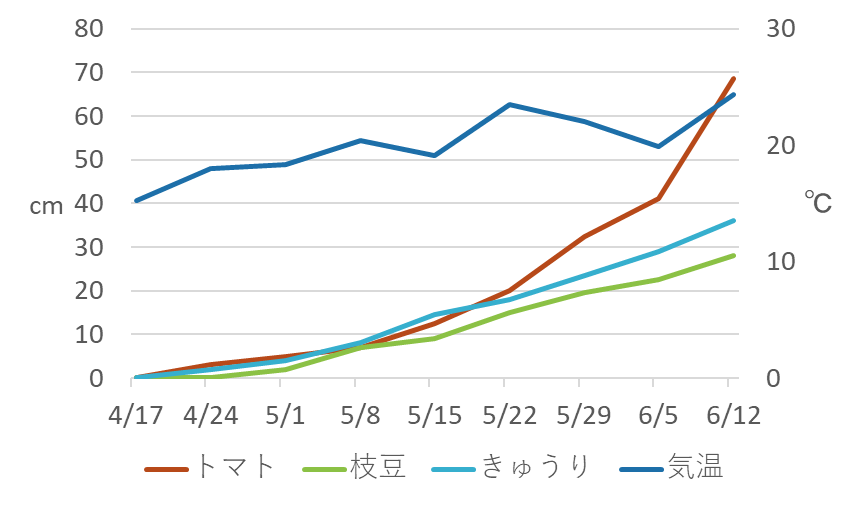
折れ線グラフ
値の連続的な変化を見るために使われる。
値の変化の大小を傾きで示す。
縦軸の左右で違うデータの軸を使うことができる。
画像参照:3-2. 時系列データをグラフにしてみよう
https://bellcurve.jp/statistics/course/18946.html
時系列データの変化を確認する
- 差分を元に確認する
(ある時点の値)-(前時点の値) - 前の値との比を元に確認する
(ある時点の値)÷(前時点の値) - 変化率を元に確認する
(ある時点の値-前時点の値)÷(前時点の値) - 指数を元に確認する
({(それぞれの時点の値)÷(基準時点の値)}×100)
(例)2009年を基準(100)としたときのそれぞれの年の時点における商品価格の指数
4. 代表値と箱ひげ図
- 平均
全てのデータの合計値 ÷ データ数 - 中央値
データを小さい順に並べたとき、真ん中の順番のデータの値のこと。
データ数が偶数個ある場合、中央に最も近い2つの値の平均値を中央値とする。
- 最頻値(モード)
出現頻度が最も多い値。
四分位数
データを小さい順に並び替えたとき、データ数で4等分した時の区切り値。
小さい順に
- 25パーセンタイル(第一四分位数)
- 50パーセンタイル(第二四分位数=中央値)
- 75パをーセンタイル(第三四分位数)
と呼ばれる。
四分位範囲=第三四分位数 - 第一四分位数
四分位数の求め方
- 中央値を求める
⇒第二四分位数が分かる - 中央値より小さい値、大きい値の2グループに分ける
※データ数が偶数個ある場合、小さい方の中央値を小さい値のグループに、大きい方の中央値を大きい値のグループに入れる。 - 小さい値のグループ、大きい値のグループそれぞれの中央値を求める
⇒第一四分位数、第三四分位数が分かる - 第三四分位数 - 第一四分位数で四分位範囲を求める
5. データのばらつき
- データのばらつきを表すのに、分散・標準偏差が使われる
- 平均値が大きく異なるデータを比較するとき、平均値に対する標準偏差の大きさを比較するほうが良い場合がある。その時、変動係数が使われる
- 変動係数=標準偏差÷平均値
6. データの標準化
レーダーチャート
いくつかの項目の大小を1つのグラフで表したグラフ。
- 各データを各項目の軸に対してプロット
- プロットした点同士を結んで多角形を表現
画像参照:6-1. レーダーチャートを作ってみよう
https://bellcurve.jp/statistics/course/19607.html
標準化
平均を0、標準偏差を1となるように変換した値。
計算結果の数値が大きければ大きいほどいい値とみなされる。
$x$:元データ、$\bar{x}$:平均値、$s$:標準偏差
\displaylines{
\frac{x-\bar{x}}{s}
}
偏差値
平均を50、標準偏差を10となるように変換した値。
- 偏差値が高いほど成績が良いことを、低いほど成績が悪いことを表す
- 平均点と同じ点数だった場合、偏差値は50になる
- 偏差値は100以上の値やマイナスの値をとる場合がある
\displaylines{
\frac{x-\bar{x}}{s} \times 10+50
}
7. データの相関
バブルチャート
3つのデータの関係性について、グラフで確認できる。
(x軸、y軸、点(バブル)の大きさ)
2つのデータの関係性のみの場合、散布図になる。
(点(バブル)の大きさが均一になる)
相関係数
2つのデータ(xとy)の関係性がどれだけ強いかを表す。
\displaylines{
\frac{xとyの共分散}{(xの標準偏差)(yの標準偏差)}
}
外れ値
他のデータと比べて大きく外れた値。相関係数の値に影響を与えることがある。
散布図で外れ値がないかなどデータを確認する必要がある。
9. 研究計画
データ収集・分析において「研究」の過程を行う。
研究の種類
観察研究
研究対象の観察によってデータを集めて解析を行う非実験的研究。(アンケートなど)
実験研究
研究対象に対して何らかの介入(薬を飲んでもらったり、治療を受けてもらったりなど)を行い、その効果を評価する研究。
研究の流れ
- 課題を設定する
- 研究計画を立てる
- データ収集
- データ分析(表やグラフなど)
- 結果の考察
データ収集について
全数調査
調査対象となる集団全て(母集団)を調べること。
標本調査
調査対象となる母集団の一部を取り出して、一部の集団(標本)で調べること。
- 単純無作為抽出法
母集団の中からランダムに標本を抽出すること