本記事は2020/9/20に、筆者の個人ブログ(閉鎖予定)で公開された記事を少し加筆したものです。
しばらく前にオンライン開催された「OngaACCELシンポジウム2020」にて、吉井和佳先生による自動採譜技術研究の発表がありました。たいへんありがたいことに、あの藤本健さんの記事でピックアップしていただき、なかなか反響があったようです。
この記事で紹介されている成果のうち、しゃをみんはコード採譜の研究に取り組んでおります。吉井先生の発表の中で、「ミラーニューロン仮説」なる概念が紹介されたあのパートです。

「生成モデル+推論モデル=VAE」 でなんかぐるぐるさせるという話をしていましたね。本記事ではこの研究成果をざっくり解説するとともに、「AI自動採譜」研究の現在地を自分なりに整理してみたいと思います。
研究内容はIEEE TASLPに掲載されています。引用してください。
一言で言うと、本研究は VAE(Variational Autoencoder) という手法をコード採譜タスクに応用してみたという話です。それだけですが、コード採譜(ひいては自動採譜全体)の研究分野では 意外にまだ誰もやってない し、やってみたら色々面白い発見もあった研究になっていると思います。
本研究の概要
- 研究の背景:音楽コード推定の研究では「生成的(generative)」と「識別的(discriminative)」の二つのアプローチがとられていた。従来の生成的手法はコード系列を潜在変数とした隠れマルコフモデル(HMM)、識別的手法は(最近は)主に深層学習による推論モデルにもう何もかも任しちゃう系。近年ではEnd-to-endも出来る後者がだいぶ優勢。
-
動機:DNN推論モデルが優秀なのはいいけど、学習に使えるデータを無限に増やせない限り天井にぶつかってる感がある。
音声認識AIはデータが無限にあってずるいよね。長らく放置されてきた「生成的手法」を、深層学習手法に取り入れることはできないか? -
提案手法: コード系列と「潜在特徴変数」 を潜在変数とし、音楽音声の特徴量(クロマベクトル)を観測値とする深層な潜在変数モデルをつくる。これをクロマベクトル→コード系列、クロマベクトル→潜在特徴変数の 推論モデル と組み合わせ、 VAE(Variational Autoencoder) の枠組みで最適化する仕組みを考案。生成モデルを定式化する際、コード系列の事前分布として マルコフモデル を設定した
(要は簡単な 言語モデル)。それにより、言語モデルと深層生成モデルでコード推論モデルを正則化する という学習機構が形成される。 - モデル実装:わりと単純。(ソースコード準備中)
- 実験結果:限られた学習データしか使わなくても精度の高いコード採譜モデルを得ることができた。言語モデルの文法を採譜モデルに教え込むこともできた。
- 結論:AI採譜モデルは単に推論モデルをがむしゃらに学習させるだけではなく、潜在変数モデルによる正則化を加えることも重要であることが分かった。
本研究や記事に対する質問・指摘などありましたらコメント、あるいはツイッターのDMまでどうぞ。
背景:識別的手法 vs 生成的手法
確率モデル的に、自動コード採譜は $\mathrm{argmax}_\mathbf{S} [p(\mathbf{S}|\mathbf{X})]$ を求める問題と記述できます。ここでXは音楽の音、あるいは音響特徴量を指し、Sはコード記号系列をあらわす変数とします。とある音楽が与えられたとき、最も事後確率が高いコード進行を求めなさい、ということですね。
この問題を解くためには $\mathbf{S},\mathbf{X}$ に関する確率モデルを定義する必要があります。確率モデルを定義する方法によって、自動採譜手法は 識別的(discriminative)手法 と 生成的(generative)手法 という二つのアプローチに大別できます。
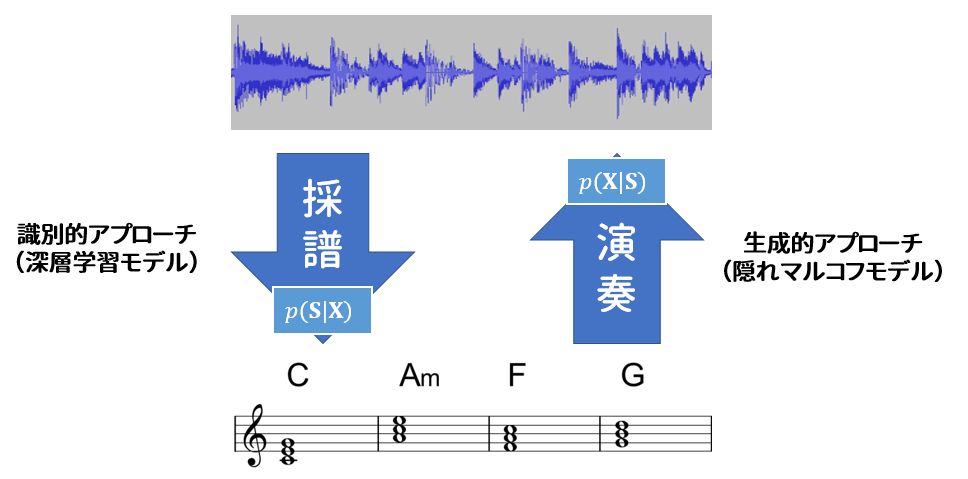
識別的手法はストレートな考え方で、ある観測値(=音響特徴量)を観測したとき、コード系列の事後確率分布がわかるモデル $p(\mathbf{S}|\mathbf{X})$ を直接作ればいいじゃない、という発想。そういうモデルを僕らは識別(discriminative)モデル、推論(inference)モデル、定かではありませんが、そう呼んでいます。深層学習ブームになってからは特に、たくさん集めた教師ありデータにモデル $p(\mathbf{S}|\mathbf{X})$ をフィットさせれば、だいたいうまく行くよね、というやり方がすっかり定着しています。
一方生成的手法は、「記号」から「音」を作る過程のモデル化を出発点とします。まずベイズの定理により、 $p(\mathbf{S}|\mathbf{X}) = \frac{p(\mathbf{X}|\mathbf{S})p(\mathbf{S})}{p(\mathbf{X})}$ となります。式を最大化するSを求める際、p(X)は無視してもいいので、冒頭の式は $\mathrm{argmax}_\mathbf{S}[p(\mathbf{X}|\mathbf{S})p(\mathbf{S})]$ と書き換えることができます。
この式は、「記号S」を入力して「音(特徴量)X」を(確率的に)生成する生成モデル$p(\mathbf{X}|\mathbf{S})$ 、およびSの言語モデル $p(\mathbf{S})$ からなっています。つまり $p(\mathbf{X}|\mathbf{S})p(\mathbf{S})$ は、作曲家 $p(\mathbf{S})$ 書いた楽譜Sを、ミュージシャン $p(\mathbf{X}|\mathbf{S})$ が演奏して音Xにした、という過程を表しています。このような確率モデルを、Sを潜在変数とする潜在変数モデル(latent variable model)と呼んでいます。
ゆえに $\mathrm{argmax}_\mathbf{S}[p(\mathbf{X}|\mathbf{S})p(\mathbf{S})]$ とはつまり、特徴量Xを観測したとき、「このXをモデルが生成する確率が一番高くなるようなSは何か」を逆算する問題になります。これを解く方法があれば、コード採譜を行うことができます。
深層学習が流行りだす前は生成モデルのほうが主流で、具体的にはコードラベル系列を「隠れ状態の遷移系列」で表現する隠れマルコフモデル(Hidden Markov Model)が用いられていました。パラメータの最尤推定や、観測値から最尤な隠れ状態系列を逆算する手法(Viterbiアルゴリズム)が確立しているので、一時期広く使われていました。
しかし、HMMは $\mathbf{S}$ にマルコフ性、$\mathbf{X}$ に時間独立性という強すぎる仮設を課しているから効率的な「逆算」が可能なのであって、そのような仮設を置かない賢いDNNで $p(\mathbf{X}|\mathbf{S})p(\mathbf{S})$ を実装しても、$\mathrm{argmax}$ を見つけるのはほぼ無理。それだからか、自動採譜界隈では深層学習で潜在変数モデルを作ろうと考える人はいませんでした。しかし、VAEを用いることで、別の角度からディープな生成モデルを活用することが可能になります。
背景:推定モデル+音楽文法
自動コード採譜に比較的近いタスクとして、自動音声認識が挙げられます。実際、HMMしかり、深層学習しかり、コード採譜の研究は常に音声認識で確立された手法を後追いする感じで発展してきた一面があります。しかし音声認識は深層学習を導入してから一気にに実用レベルにまで進化してしまった一方、コード採譜はまだそこまで飛躍的に良くなってません。だいぶ賢くなったとはいえ、「そうはならんだろ」みたいな変な間違いもちょくちょく起こします。
当然 「文法(言語モデル)に照らし合わせて直す」 ということを考える流れになります。これも非End-to-endな音声認識では必ずやることです。DNNが推定した単語の事後確率と、言語モデルに対する尤度を掛け算して、ビタビ探索なりビームサーチなりで一番確率が高い系列を推定するわけです。(理論的には、推定器として学習されたDNNの出力を $\mathrm{argmax}_\mathbf{S}[p(\mathbf{X}|\mathbf{S})p(\mathbf{S})]$ における $p(\mathbf{X}|\mathbf{S})$ だと強引に解釈することで式を解いていることになります。しかしとてもうまく動いているのであんまり問題視されていません。)
この方法は、推論モデルによる推定結果を事後的に修正する、後処理手法(Post-filtering)にあたります。別々に学習した推論モデル・言語モデルを組み合わせる方法として自然に思いつくパターンですね。
一方ここで紹介するVAEに基づく手法も、吉井先生が紹介された通り「推論モデルと生成モデルを組み合わせる」「音楽文法を使って修正する」ことを意図していますが、上述の手法と根本的に異なるのは、「生成モデル(言語モデルも含む)を使って推論モデルを鍛える」 というアプローチであることです。つまり、推論モデル自体をもっと賢くする方法はあるのか(アノテーションをとにかく増やす以外で)、という問題に対する解決手段であり、これはEnd-to-endなモデルを鍛えるのに役立つかもしれません。
VAE(Variational autoencoder)とは要するに、「潜在変数の事後分布を(教師無し学習で近似的に)逆算できるDNN系潜在変数モデル」。何かと話題になる「GAN」と並び、「何か(主に顔写真)を合成する魔法」というイメージのせいで、自動採譜の研究ではスルーされがちだったのかもしれません。しかしうまく使えば、より賢いコード採譜モデルを鍛えるのに役立つ手法になるのです。
VAEの使い方
VAEは 「潜在変数の事後分布を(教師無し学習で近似的に)逆算できるDNN系潜在変数モデル」 です(2回目)。たとえばMNISTで学習する元祖VAEは、潜在変数から手書き数字画像を合成するDNN生成モデル(いわゆる デコーダー)と、手書き数字画像が生成された場合の潜在変数の確率分布を変分推定の要領で推定するDNN推論モデル(いわゆる エンコーダー)からなっています。両方を一緒に教師なし学習させるとあら不思議、画像が何の数字か教えてないにもかかわらず、ちゃんと数字の概念を理解したかのごとく、潜在空間が 良い感じになった(語彙力…)生成モデルと推論モデルに勝手になっていくのです。
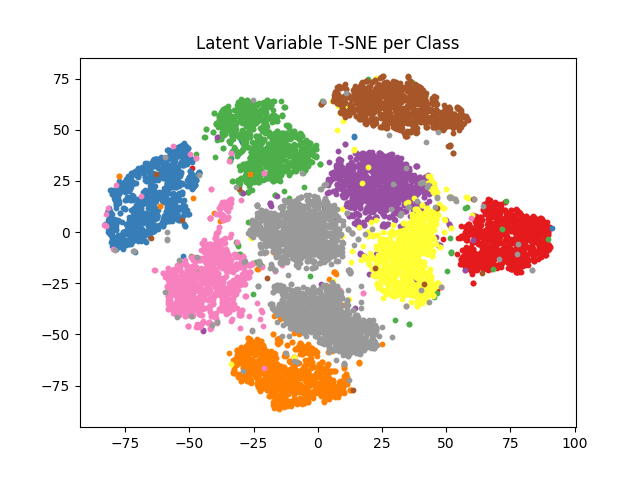
このVAEを拡張し、「数字」という明示的な情報も生成モデルの入力とみなし、画像から数字を推定する推論モデルも導入します。すると、このモデルは正解ラベルがある画像、無い画像の両方を使って学習出来るようになりました。これがSemi-supervised VAEです。不思議なことに、学習に使う正解ラベルが無い画像を増やすと、手書き数字認識の正解率が上がる のです。学習データ量が増えて「良い感じ」になった生成モデルが、正解ラベルに代わって数字認識用の推論モデルを「教えている」 のです。
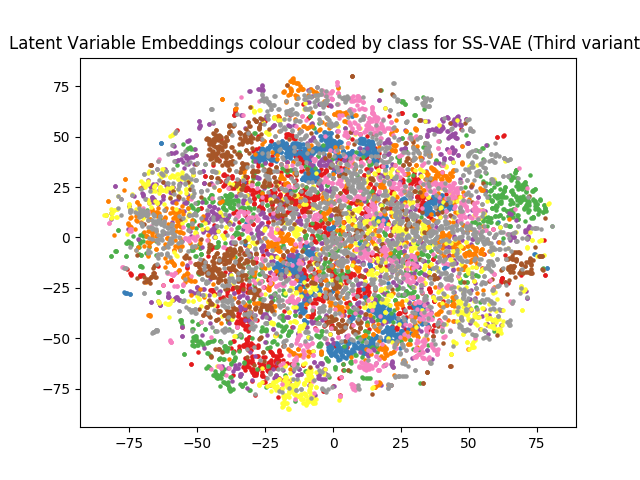
この推論モデルを、コード進行系列の確率を推定する推論モデルに置き換えれば、コード採譜モデル用のSemi-supervised VAEになります。そうすることで、「採譜」をするモデル $p(\mathbf{S}|\mathbf{X})$ と、「演奏」をするモデル $p(\mathbf{X}|\mathbf{S})p(\mathbf{S})$ を統一的に最適化する学習機構が形成されるのです。手書き数字認識のように、コード採譜も精度が上がったら嬉しい!
実装と損失関数
VAEの理論は割愛し、実装を見ていきます。確率変数は以下のように表記します。
- $\mathbf{X}$:クロマベクトル系列(観測値)。ベルヌーイ分布に従うバイナリ値(と言いつつ実際はMNISTみたいに0~1の実数値をとる)ベクトル。
- $\mathbf{S}$:コードラベル系列(潜在変数)。離散分布に従うone-hotベクトル。
- $\mathbf{Z}$:潜在特徴系列(潜在変数)。ガウス分布に従う実数値ベクトル。
これらの変数に関する確率モデルを3つのDNNで実装します。
- $p_\theta(\mathbf{X} | \mathbf{S}, \mathbf{Z})$:生成モデル(VAEでいうところのデコーダ)。SとZの結合を入力し、ベルヌーイ分布を吐くDNN。
- $q_\alpha(\mathbf{S}|\mathbf{X})$:Sの推論モデル(VAEでいうところのエンコーダその1)。Xを入力し、softmax関数で正規化した離散分布を吐くDNN。
- $q_\beta(\mathbf{Z}|\mathbf{X})$:Zの推論モデル(エンコーダその2)。Xを入力し、ガウス分布のパラメタを吐くDNN。
潜在特徴系列Zという謎の変数ですが、特徴量Xの生成分布を推定するには、離散的な変数Sだけを潜在変数にしても明らかに情報量が足りないので、連続的な変数を補足しておこう・・・という考えから導入された抽象的な概念です。要は前出のSemi-supervised VAEの、あの「良い感じではなくなった」潜在空間のことですね。
DNNはいずれも双方向LSTM。学習の安定性のため最後にLayer Normalizationを挟んだ以外、とくに凝らした実装ではないです。
また、Sの事前分布 $p_\theta(S)$ には、DNNではなくマルコフ型言語モデルを設定しています。自己遷移確率が高いマルコフモデルを設定することで、「コード系列はある程度同じラベルを繰り返してから次のラベルに切り替わる」という、とても素朴な文法を設定します。
これまで定義されたモデルの関係をまとめると以下の図のようになります。X→S,ZのモデルとS,Z→Xのモデルが、閉じた輪を形成する形です。
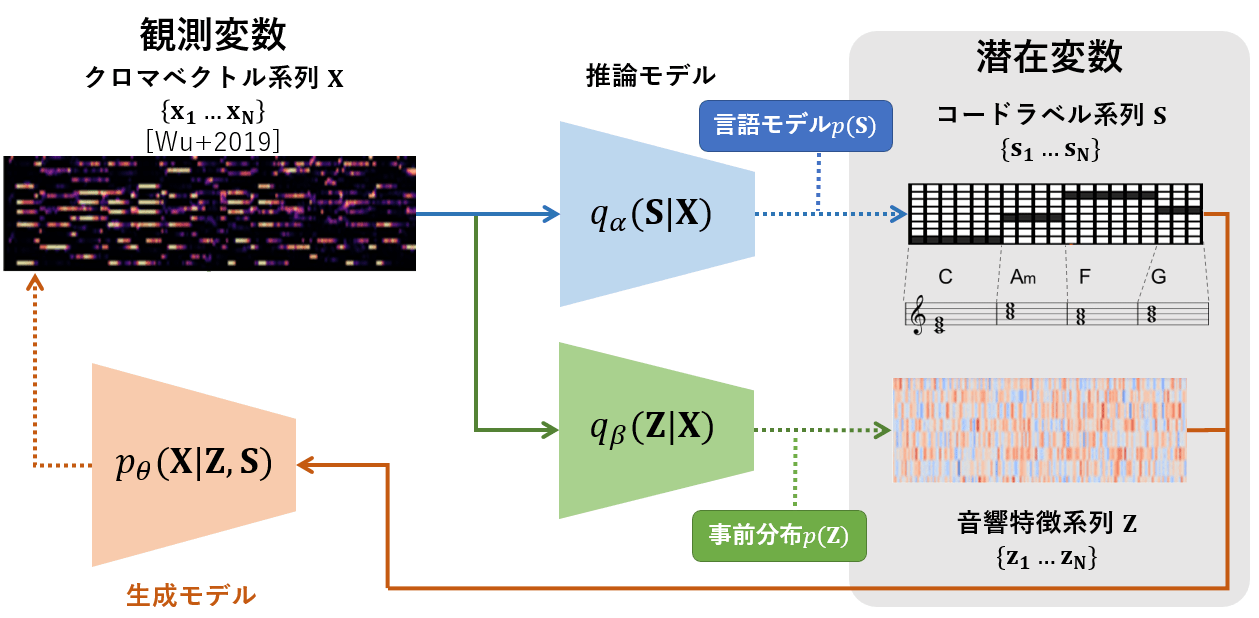
学習データはXのみの場合、最大化目標関数は:
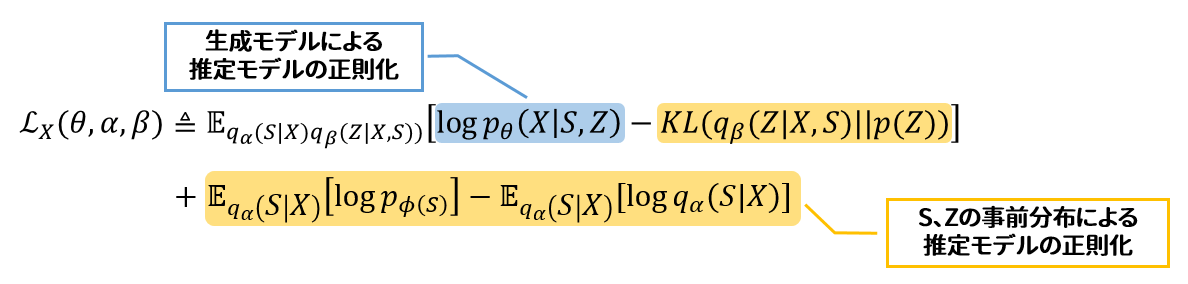
いわゆる再構成尤度と、潜在変数の正則化項からなるもので、VAEが分かる人にとっては特に変哲の無い目標関数であるはずです。特筆すべき点として、Zの正則化項(1行目の黄色パート)と違い、Sの正則化項(2行目の黄色パート)はSをサンプリングしなくても解析的に(かつ微分可能な計算式で)期待値が求まります。
最大化すべき目標関数を見ていきます。XとSのペアデータが与えられた場合、目標関数は:
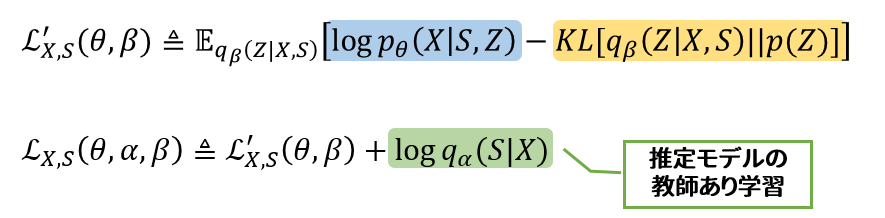
よって最終的な目標関数は:
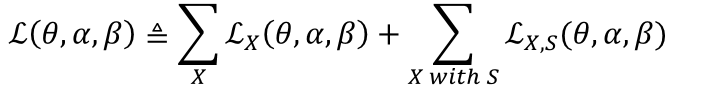
つまり両者の和になります。損失関数はこれのマイナス。
学習に使う音楽Xには正解ラベルSが付いているものを使う必要がありますが、正解ラベルが無い音楽を含めることができます。この場合 $\mathcal{L} _{\mathbf{X}}$ のみを最適化し、 $\mathcal{L} _{\mathbf{X},\mathbf{S}}$ の学習は行いません。これが半教師あり学習になるわけですね。
推論時は従来のDNN法と同じく、推論モデル $q_\alpha(\mathbf{S}|\mathbf{X})$ のみを使ってSの事後分布から直接求めます。
目標関数 $\mathcal{L}$ を最大化することで、$q_\alpha(\mathbf{S}|\mathbf{X})$ は:
- 推定した事後分布が正解データに近づくように
- 言語モデル尤度が高まる(=コード遷移頻度が減る)ように
- 推定結果を生成モデルに入力すると、正しい音響特徴が再構成されるように
学習されていきます。言語モデルと生成モデルが、推論モデルを 正則化 する形になるのです。これがVAEによる性能向上のメカニズムです。
アノテーション付き音楽を用いた実験でも、VAEを用いた学習の結果推論モデルの採譜正解率が上がったこと、そして採譜結果の言語モデル尤度がより高くなったことが確認できました。正解データがある楽曲およそ200曲を用いて学習するだけで、ほぼ1000曲分の正解ラベルを用いて教師あり学習のみをした推論モデルと同等レベルの性能にまでなりました。
今後の課題
事前分布 $p(\mathbf{S})$ は素朴なマルコフモデル、DNNはとりあえず全部双方向LSTMにするなど、具体的な実装はわりと雑です。それでもちゃんと効果が見られたので、個々のコンポーネントをもっと工夫していけば、まだまだ向上の余地は大いにあるとでしょう。たとえば、下記のような研究ができると思います。
- 隠れ変数を増やす:調、拍、音符など、隠れ変数にほかの音楽要素を導入して階層的な生成モデルを作り、さらに大きなVAEを定式化する。「コード進行・音符は調に従う」「コード進行は拍に合わせる」といった音楽文法に従う、さらに賢い多機能耳コピモデルが作れるかも。
- ちゃんとしたコード系列モデル:今回はコード系列の「言語モデル」として、単純なマルコフモデルを決め打ちしたが、コード進行のパターンなど、複雑な音楽文法も評価してくれる言語モデルに置き換えれば、特に半教師あり学習がもっと効果的になるのでは?と期待できる。
まとめ
生成モデルを作って推論モデルの学習を助けるというアプローチ自体は近年の音楽情報処理研究でもぽつぽつと出てきているみたいです。AIといえばとにかく教師ありデータと、ウルトラ深いEnd-to-endモデルで殴っとけというイメージがありましたが、理論面でもまだ仕事が全然残っている、という認識が広がりつつあるんじゃないでしょうか。
「AI採譜の正解率が少し上がった!」的な結果も、研究に取り組む自分にとってはとても喜ばしい成果ではありますが、一番重要な事はこの研究を通して、「音楽を理解する」とは何か?という問いの答えにほんの一歩、近づけた気分になれたこと ではないでしょうか。つまり、音楽の生成(≒創作、演奏)と識別(≒採譜)は、人間の脳内では表裏一体であること。人間は機械的に音を記号に当てはめているだけ(=従来的な識別的手法)ではなく、「作曲」能力も駆使しながら「耳コピ」している のであり、深層学習を用いてこの原理を再現することができるのです。
吉井先生が発表した成果は、再現への第一歩を踏み出せたに過ぎません。さらに二歩三歩進めていけるよう、これからも頑張っていきます。