【注目論文】Sinusoidal Frequency Estimation by Gradient Descent

QMULのBen Hayes氏らが、勾配降下法で周波数推定を行う手法を論文で発表しました。ICASSP2023に投稿したそうです。
きわめてシンプルな手法なのですが、機械学習系音声合成にとってはたいへん重要な成果だと思うので、紹介します。

論文リンク：Sinusoidal Frequency Estimation by Gradient Descent
ソースコード：https://github.com/ben-hayes/sinusoidal-gradient-descent

背景：DDSPの限界

DDSP(Differentiable Digital Signal Processing)とは、微分可能な計算式を持つDSPモジュールをDNNに組み込んで機械学習をやる手法で、Google Magentaプロジェクトが最初に打ち出したアイデアです。

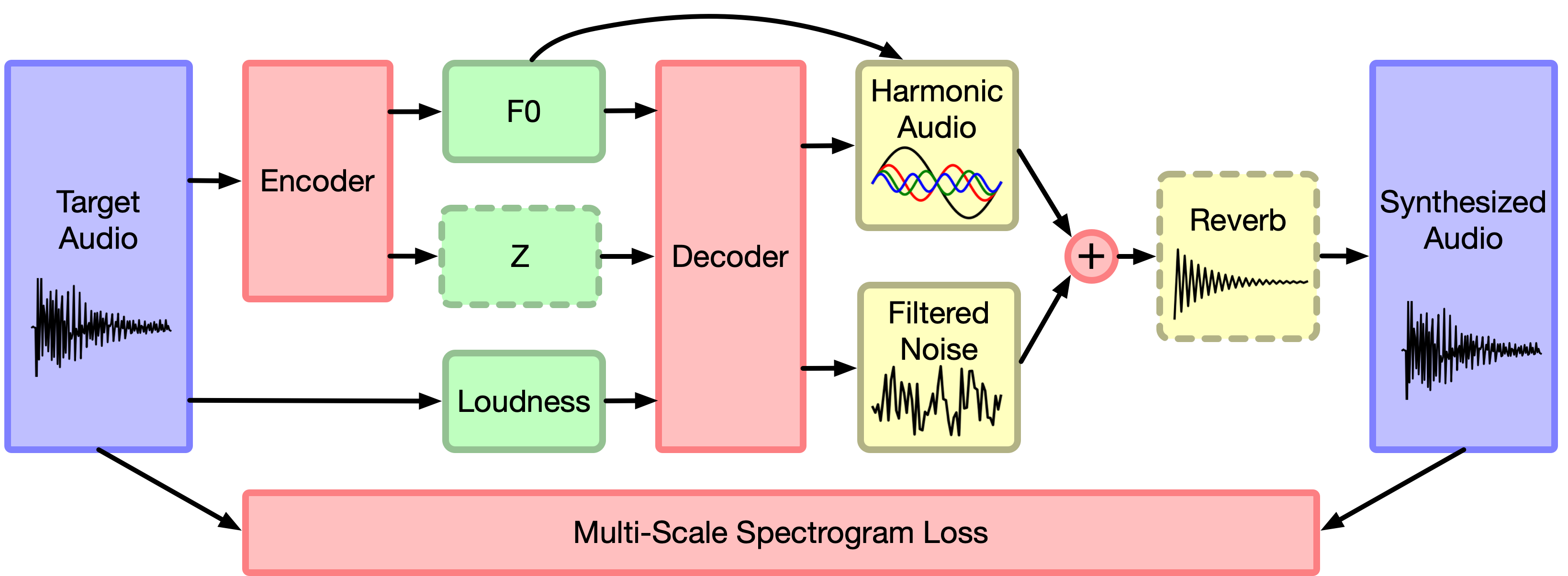
今ではもうDDSPシリーズと呼べるほど多様な応用が提案されていますが、大抵はDSPをDNNの最終端に設置して、「DSPのパラメーターをDNNで学習する」という形をしています。
Magentaの元祖DDSPモデルは、ピッチ（基本周波数）列を入力すると、オシレーターから出力された周期信号とノイズ信号にDNNデコーダーが出力したフィルターを掛けることで、楽器音を合成する仕組みになっています。
合成音声と目標音声の差を損失関数とし、損失はフィルターを通してデコーダーに伝播し、デコーダーが学習されていきます。

ところで、オシレーターも重要なDSPモジュールの一つです。ほかのDSPモジュールのように、デコーダーにパラメーター（周波数）を学習・推定してほしいところなのですが・・・ここがそうはいかないのです。周期信号のオシレーターは、入力された基本周波数とその倍音の正弦波を重ねて出力するだけなので、デコーダーは周波数を決めません。

周期信号オシレーターは三角関数なので、当然微分可能です。デコーダーに損失を伝播させることはできるはずですが、なぜDNNは周波数を学習できないのでしょう？

背景：なぜ周波数は学習できない？

単純な正弦波で考えます。角周波数が$\omega$のとき、正弦波信号は以下の式で生成されます。

x_n=A\cdot cos(\omega n+\phi)

とりあえず、振幅$A$と初期位相$\phi$は既知とします。
とある目標正弦波に対して、未知の変数である$\omega$を推定したいです。

適当な値で$\omega$を初期化したあと、目標正弦波との距離(Mean Squared Error, MSE)を計算し、勾配降下で$\omega$を更新し続ければ、正しい周波数に辿り着けるでしょうか？

残念ながらそうはいきません。
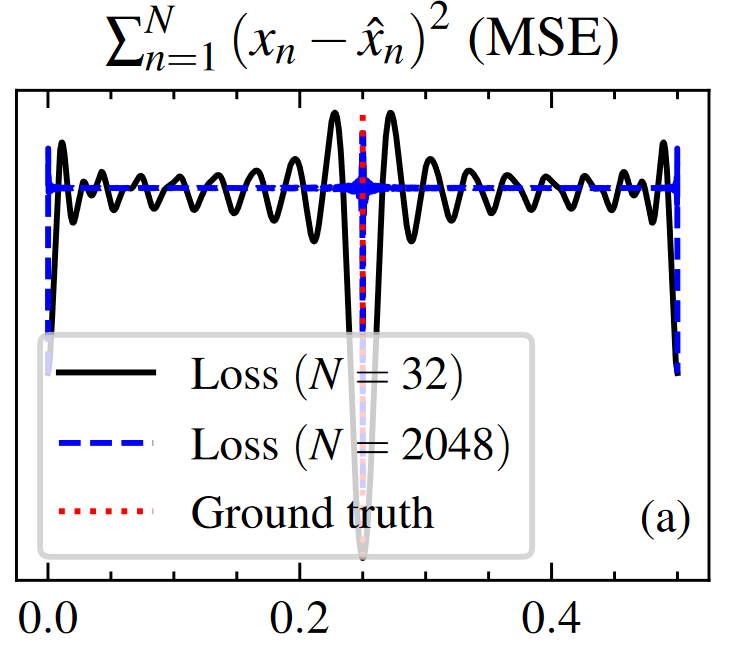
あらゆる$\omega$による生成正弦波と、目標正弦波とのMSEを計算してみると、こうなります（図は論文から引用）。

$N$は信号の長さです。
真ん中の一番低い地点が最適解ですが、$N=32$の場合（黒線）を見ると、前後がぼこぼこで局所解だらけになっています。
$N=2048$の場合（青点線）に至っては、正解ジャストの地点以外はほぼ真っ平。勾配降下法で正解の周波数にたどり着くことは不可能です。

人間の感覚とは真逆ですね。音叉を鳴らしながら楽器をチューニングする作業を想像してみてください。音高を低く調節すべきか、高く調節すべきかは、チューニングのズレが大きいほどはっきり分かり、逆にズレが小さくなるほど確信が持てなくなるのが私たちの感覚です。
一方音声の波形およびスペクトログラム同士の引き算は、私たちが知覚してるような 「音高の差」を正しく表現できないのです。
ゆえに、波形やスペクトログラムの差を損失関数とする音声波形生成DNN（WaveNet, MelGANなど）は、音の周期的特性を学習するのにかなり苦労しています。

参考文献：I'm Sorry for Your Loss: Spectrally-Based Audio Distances Are Bad at Pitch

とにかく、これではオシレーターをディープラーニングに組み込むことはできません。
できたらなぁ、と思ってた人は少なくないはず。

提案法：複素関数オシレーター

Ben氏は、複素数$z$で正弦波の角周波数を表す正弦波オシレーターを考えました。

s_n(z_\omega)=|z_\omega|^n cos{n\angle z_\omega}

$z_\omega$の角度$\angle z_\omega$は角周波数、絶対値$|z|$は正弦波の減衰指数をあらわします。
生成するのはただの正弦波ではなく、$n$が増大するにつれて振幅が増幅（$|z_\omega|>1$）あるいは減衰（$|z_\omega|<1$）しうる正弦波ですね。

このオシレーターは複素数を入力し、実数を出力する関数です。厳密には、複素数入力に対して微分不可能です。ただし、関数の変数を$z_\omega, \overline{z_\omega}$と見なせば、ウィルティンガーの微分を用いて、変数$z_\omega$（と$\overline{z_\omega}$）の偏微分を求めることができます。

今度はこのBen氏オシレーターの出力と目標正弦波のMSEからウィルティンガーの微分を求め、勾配を複素空間内で可視化してみます。

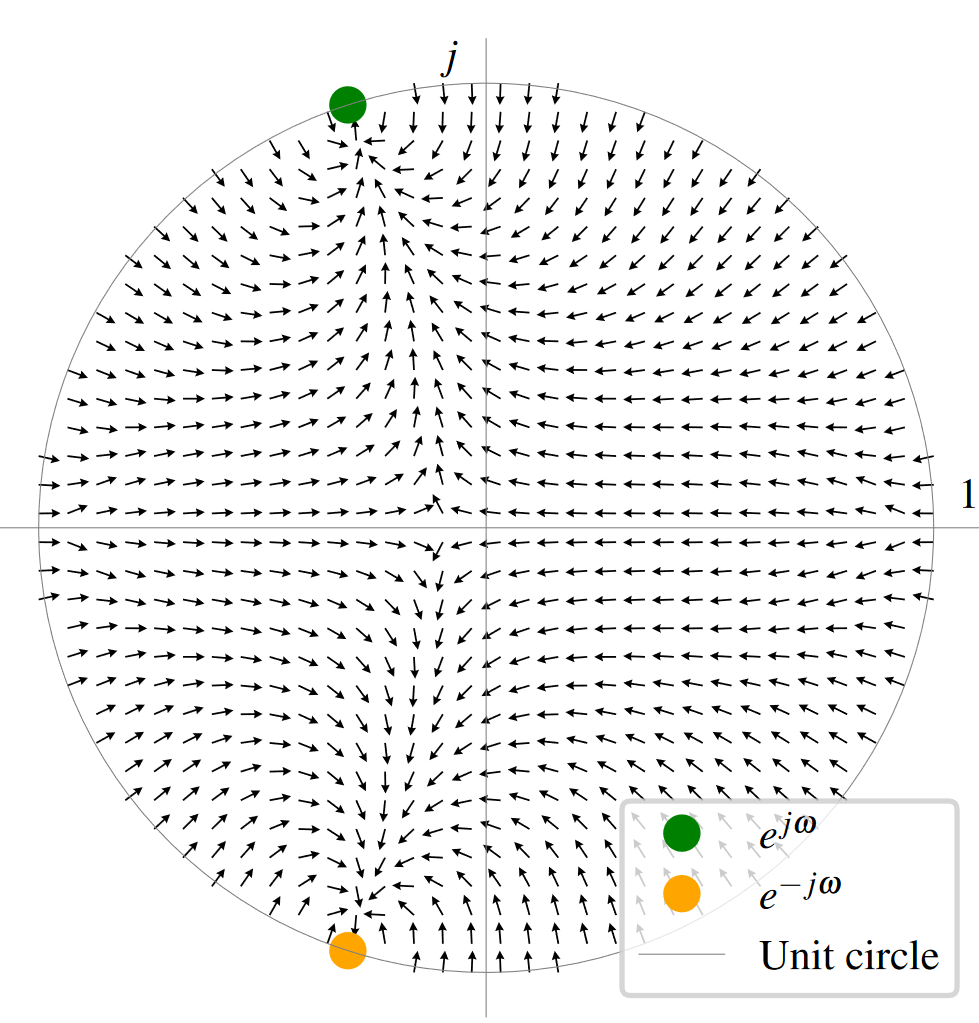
緑の点が最適パラメーターです。複素空間内のいかなる地点からも、勾配を辿って最適解にたどり着けるようになっています！
勾配の向きを観察してみます。$z_\omega$を単位円上の適当な値に初期化すると、生成正弦波はまず振幅減衰がかかるように変化します。続いて、正しい周波数に近づいていきながら、また徐々に振幅減衰が無くなり、目標正弦波に収束します。

振幅減衰が無い（$|z_\omega|=1$）と、$z_\omega$は単位円の上でしか動けなくなるので、局所解にはまってしまいます。振幅減衰を導入し、$z_\omega$が単位円の中に動けるようにしたことで、局所解を回避できたのです。

提案法拡張：振幅・初期位相・複数正弦波

振幅と初期位相を表す複素数$z_\phi$を変数に追加して、オシレーターを拡張します。

s_n(z_\omega, z_\phi)=|z_\phi||z_\omega|^n cos(n\angle z_\omega + \angle z_\phi)

振幅と初期位相も同じように、勾配降下法で正解に辿り着くことができます。

さらに、複数の正弦波を重ねれば：

s_n(z_\omega, z_\phi)=\sum_k( |z_{\phi_k}||z_{\omega_k}|^n cos(n\angle z_{\omega_k} + \angle z_{\phi_k}) )

複数の正弦波パラメータを同時に最適化し、生成波形を複雑な音声波形に近づけることができます。
この能力こそが、本提案手法の真価だと思います。勾配降下法で複数のパラメータを同時に推定できるのであれば、先述のDDSPでも、オシレーターからデコーダーに損失を伝播し、パラメーターを推定するようデコーダーを学習させることが可能になります。

オシレーター、待望のDDSPの仲間入りです。これはデカい。

実装

単一正弦波周波数推定をPyTorchで書いてみます。PyTorchのtorch.abs()やtorch.angle()は複素数入力に対してウィルティンガー微分を計算してくれるので、普通にautogradに任せればOK。便利！

# ライブラリ読込
import torch
import torch.nn.functional as F
import tqdm

# 減衰正弦波オシレーター
def exp_decay_sinusoid(z_omega, z_phi, n):
    arr_n = torch.arange(n)
    magnitude = z_omega.abs().pow(arr_n) * z_phi.abs()
    sinusoid = torch.cos(arr_n*z_omega.angle() + z_phi.angle())
    return magnitude * sinusoid

# 複素数パラメータ初期化
# 単位円上の適当な値で初期化します。
init_freq = torch.rand(1)*torch.pi
init_phase = torch.rand(1)*torch.pi
param_omega = torch.exp(init_freq*1.0j).requires_grad_()    # 角周波数・減衰係数パラメーター
param_phi = torch.exp(init_phase*1.0j).requires_grad_()     # 振幅・初期位相パラメーター

# 目標正弦波を作成
# 長さ4096、周波数・振幅・初期位相ともにランダム
signal_length=4096
target_freq = torch.rand(1)*torch.pi
target_mag = torch.rand(1)
target_phase = torch.rand(1)*torch.pi
target_sinusoid = torch.cos(torch.arange(signal_length) * target_freq + target_phase) * target_mag

# 初期・目標パラメーターをプリント
print(f"Initial freq/mag/phase: {param_omega.angle().item():.4f} / {param_phi.abs().item():.4f} / {param_phi.angle().item():.4f}")
print(f"Target freq/mag/phase: {target_freq.item():.4f} / {target_mag.item():.4f} / {target_phase.item():.4f}")

# 勾配降下ループ
optimizer = torch.optim.Adam([param_omega, param_phi], lr=1e-4)
for i in tqdm.tqdm(range(50000),desc="Gradient descent"):
    # パラメーターから減衰正弦波を生成
    estimated_sinusoid = exp_decay_sinusoid(param_omega, param_phi, signal_length)
    # 損失関数：Mean Squared Error
    loss = F.mse_loss(estimated_sinusoid, target_sinusoid)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

print(f"Loss: {loss.item()}")
print(f"Estimated freq/mag/phase: {param_omega.angle().item():.4f} / {param_phi.abs().item():.4f} / {param_phi.angle().item():.4f}")

出力の一例です。

Initial freq/mag/phase: 1.9911 / 1.0000 / 2.7615
Target freq/mag/phase: 2.6627 / 0.3807 / 1.9458
Loss: 1.5850519048399292e-05
Estimated freq/mag/phase: 2.6627 / 0.3807 / 1.9456

ループ終了後、パラメーターparam_omegaとparam_phiはちゃんと正しい角周波数・振幅・位相をあらわしています。

複数の正弦波パラメーターで複雑な波形を再現したい場合も、同じように勾配降下法でパラメーターを推定できます。
トランペットの波形を与えてみたところ、長さ1024の波形を64個の正弦波の組み合わせでしっかり再現することができました。

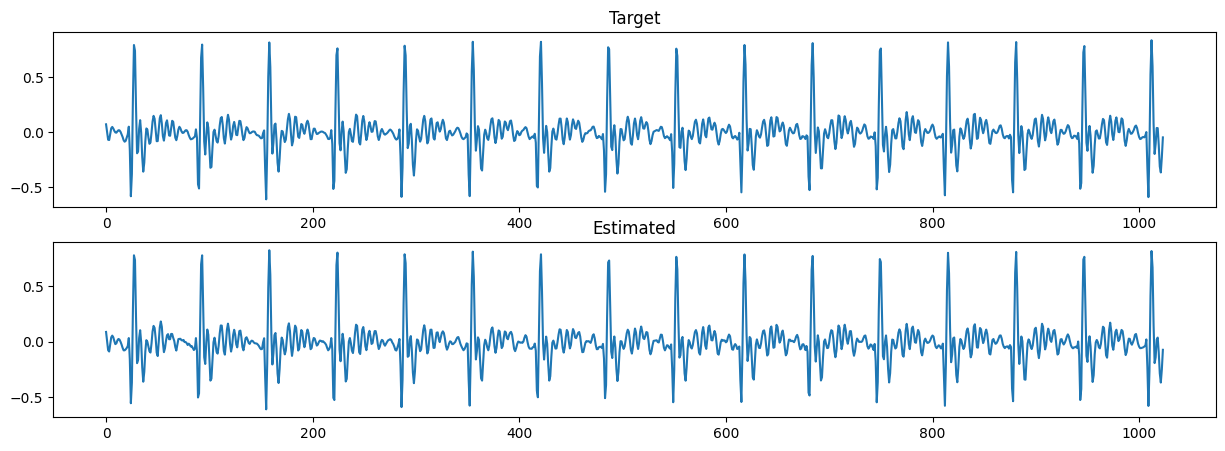
もちろんパラメーター数を増やせば、さらに複雑な波形も再現できます。

まとめ

勾配降下で周波数推定をする方法が見つかりました。
平たく言えば、「コンピューターは遂に「音の高低」を理解した」と言えるほどの大きな進歩です。DNNに音の周期構造を学習させるのが、かなり楽になると思います。

オシレーターを機械学習に組み込むことが可能になったので、間違いなく、これを応用した進化版DDSPはすぐに出てくるはずです。バイオリンやトランペットなどの単音高楽器だけでなく、パーカッション・人声・果てには複数楽器の合奏など、遥かに複雑な構造をもつ音を生成することが可能になるでしょう。

他にも、正弦波オシレーターに勾配降下が使えないが為に、滞っていた沢山のアイデアが次々と試されるはずです。常にコンピュータービジョン界隈に後れを取りがちな音声・音楽系AI技術が、これからどう進化するか見ものですね。