武蔵野 Advent Calendar 2018の6日目らしい.

暗号技術の安全性証明と攻撃の関係

暗号技術に安全性証明が求められる時代です. (プリミティブ以外で安全性証明が付いていないものは見なかったことにしましょう)

暗号学者・技術者は計算量理論的な安全性証明で何を行っているのでしょうか. 基本的には数学的な定理として, 「問題Aが難しいときに, ある暗号方式Bは安全」や「暗号技術Aが難しいときに, ある暗号方式Bは安全」といったことを示しています. ¹　

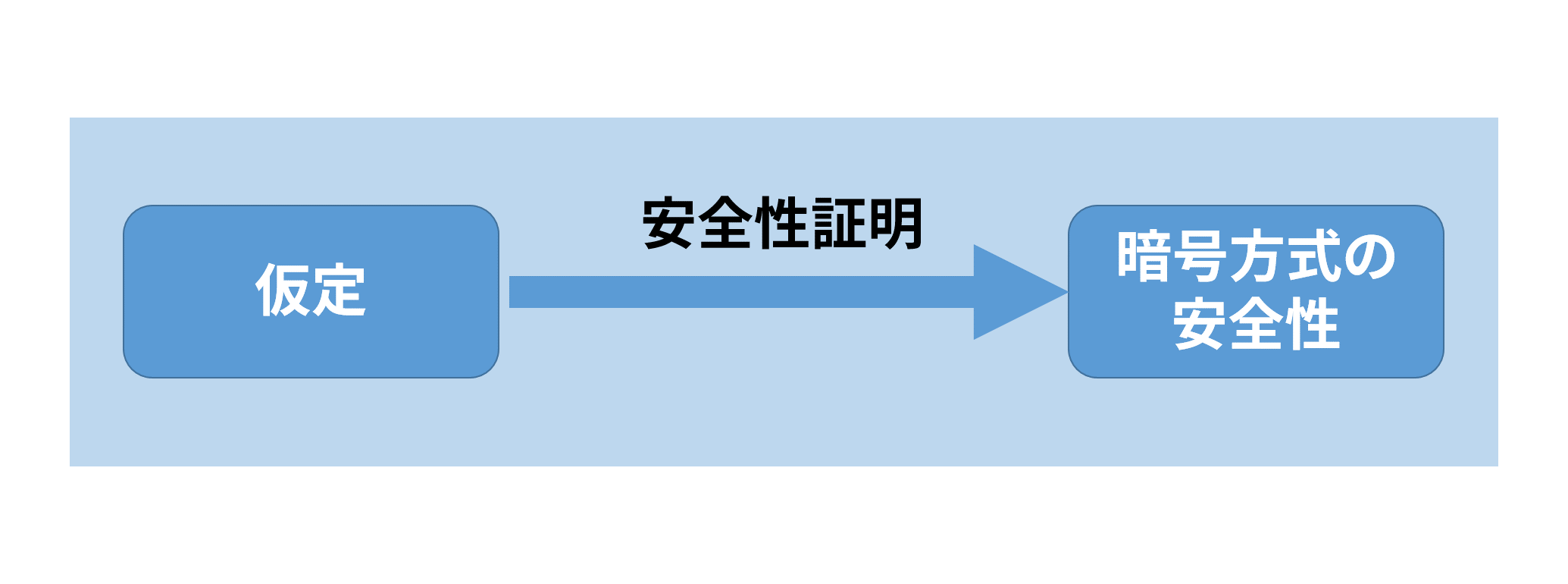
暗号技術に攻撃があった場合, どのようなことが考えられるでしょうか? 色々なケースが考えられますが, 大体以下の

証明も仮定も強度もあるしモデル内だが, 実装が間違っていた
証明も仮定も強度もあるが, モデル外の攻撃だった
証明も仮定もあっているが, 強度不足だった
証明はあっているが, 仮定が間違っていた
証明が間違っていた
証明がなかった

となると思います.

それぞれについて事例を交えて解説していこうと思います.

1. 証明も仮定も強度もあるしモデル内だが, 実装が間違っていた

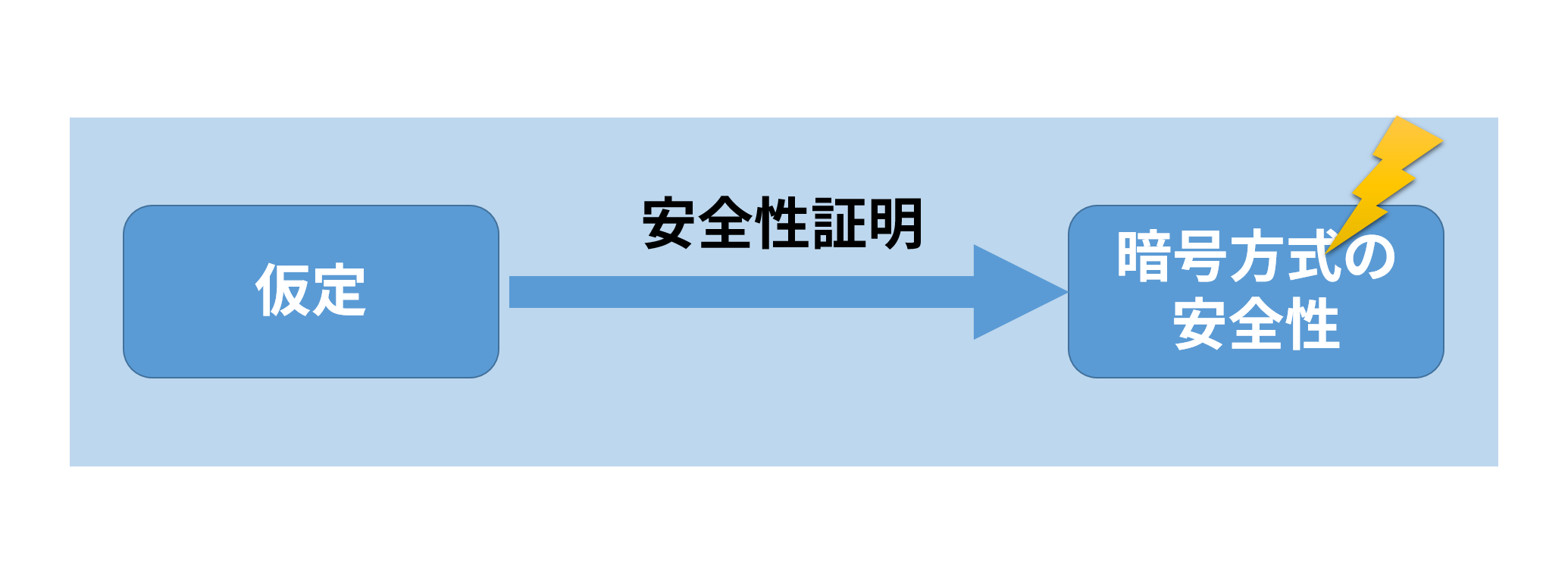
「暗号方式」のところに雷マークがあります. プロトコルや方式は正しいけれでも, ソフトウェア実装やハードウェア実装する際に間違えてしまうこともあります. セキュリティ界隈で色々と紹介されているので省略します.

2. 証明も仮定も強度もあるが, モデル外の攻撃だった

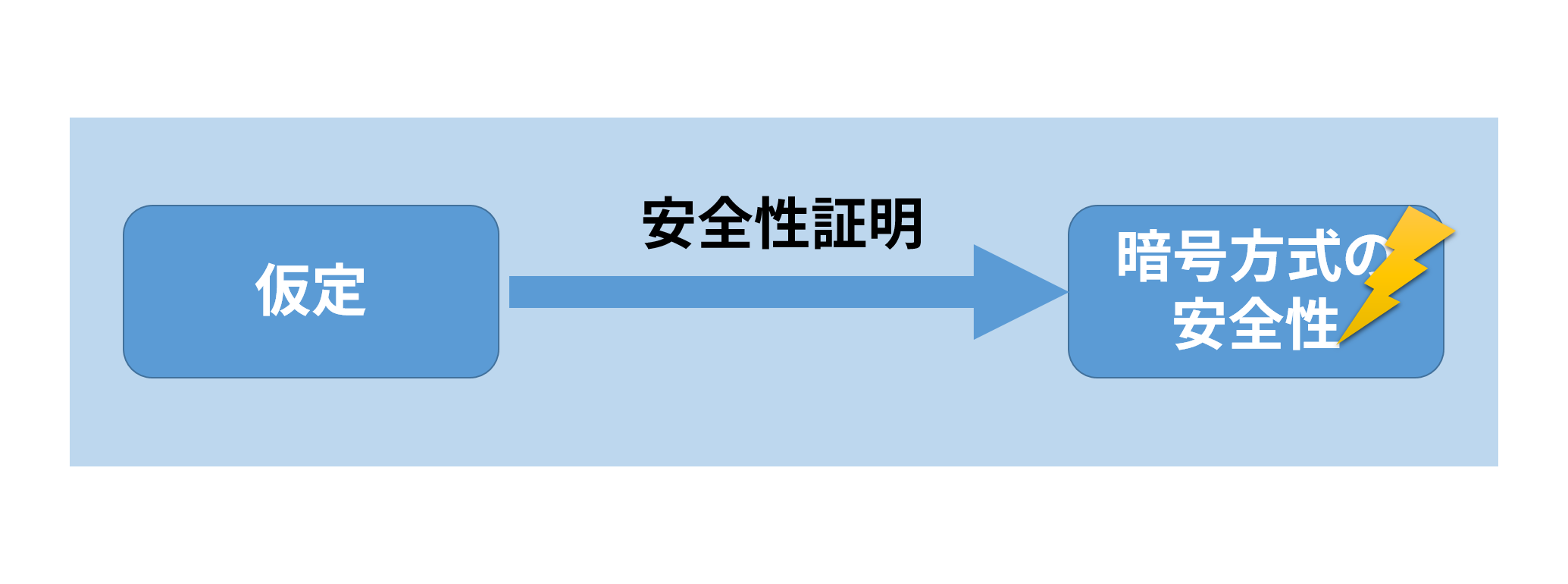
「安全性」のところに雷マークがあります. これは安全性を定義する際の攻撃モデルの外からの攻撃という気持ちです.

2-1. 理想化された特殊なモデル vs. 現実の計算

安全性証明を特殊なモデルで行うとして, そのモデルは現実を上手く反映しているのでしょうか？

Generic GroupモデルやGeneric Ringモデル, また, その亜種が特殊なモデルとして有名です.

識別不可能難読化 (iO) の構成では提案と攻撃の連鎖が長く続いたため, 元にする多重線形写像を理想化したモデルの下で安全性証明が行われることがあります. 一部の提案では, 証明で想定していたモデルの外からの攻撃がありました.

2-2. 弱い攻撃モデル vs. 強い攻撃モデル

適切な仮定の下で選択平文攻撃の下で識別不可能 (IND-CPA安全) な公開鍵暗号は多々ありますが, これらに対して選択暗号文攻撃が有効なことはあります. 例えば, ElGamal暗号はDDH仮定の下IND-CPA安全ですが, OW-CCA2安全ではありません準同型性を用いると, ターゲット暗号文を変形した暗号文を復号してもらうことで, ターゲット暗号文の平文を得ることが出来ます.

また別の例として, 古典計算機では（今のところ）攻撃できないが, 量子計算機では攻撃できる暗号もあります. （RSA暗号やElGamal暗号等）

2-3. 抽象化 vs. 物理

適切な仮定の下で選択暗号文攻撃の下で識別不可能 (IND-CCA2安全) な公開鍵暗号は多々あります. この安全性は, 復号鍵が刺さった復号機械をブラックボックスに使えても, 復号鍵を得られないということを意味します. （逆に復号鍵が得られるならば, 識別不可能性が敗れる. ）しかし, 復号機械からは, 電力消費量や計算時間のばらつきのように, さまざまな情報が漏れることがあります. また, 復号機械に計算させる間にわざと故障を起こすことも出来るでしょう. このように計算量理論的にで抽象化された攻撃モデルの外の攻撃も色々と考えられています.

3. 証明も仮定もあっているが, 強度不足だった

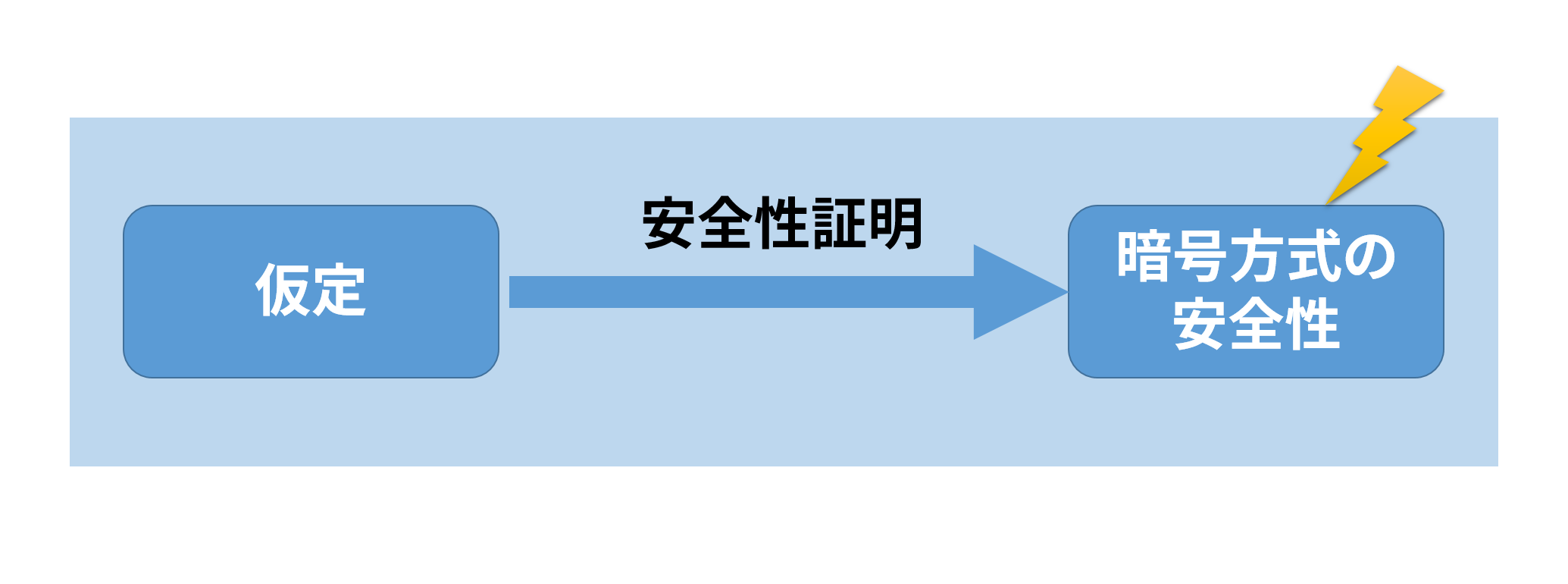
「暗号方式の安全性」自体に雷マークがついています. これくらいのパラメータを使えば安全だろうと思ったら, そうでないということもあるでしょう.

Akiyama et al. (SAC 2017) のIECという公開鍵暗号方式 ² はある仮定に基づいてその安全性を証明していました. しかし提案パラメータ1で解読実験を行うと, 30--40秒ほどで復号鍵を復元できることが分かりました. また, 提案パラメータ2でも, 30--40秒ほどで平文の識別攻撃が出来ることが分かりました. ³

4. 証明はあっているが, 仮定が間違っていた

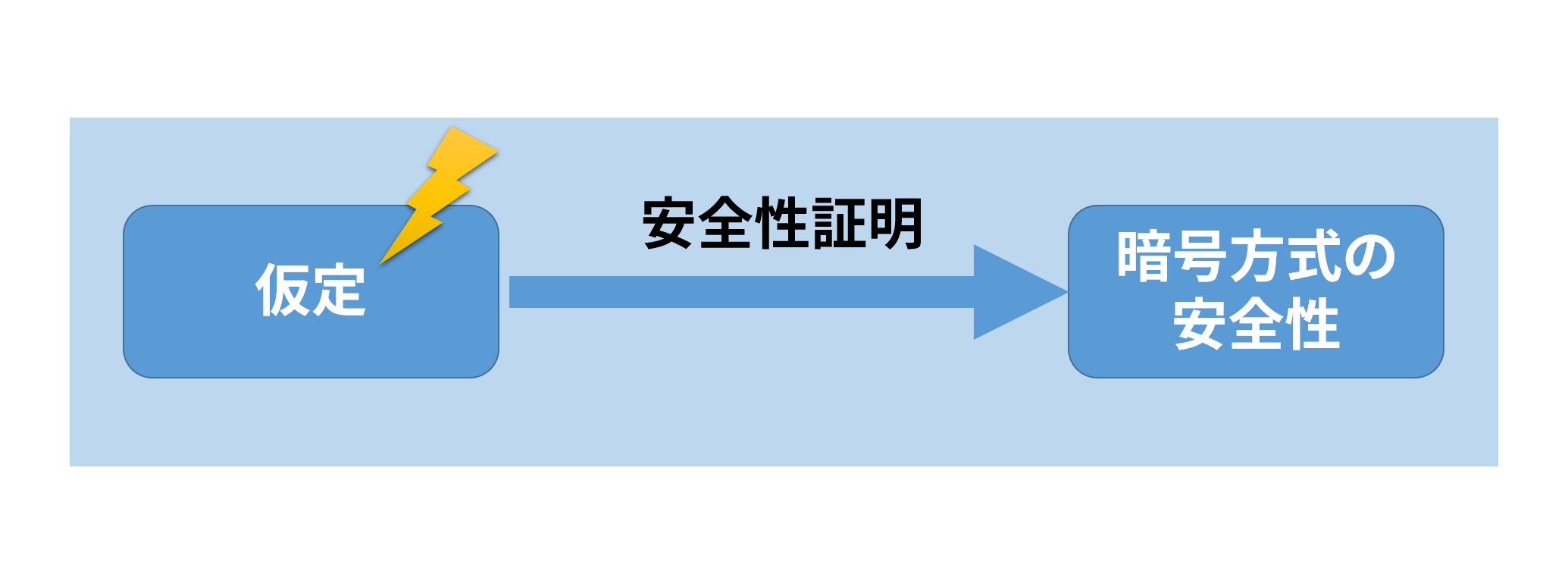
「仮定」に雷マークがついています. 「問題Aは難しい」という仮定が実は間違っていたケースもあります. この場合, 「問題Aは難しい」という仮定が間違っていたのであって, 「問題A'は難しい」という別の仮定から別の証明が付く可能性が残っています. 具体的に攻撃を行うことで, 別の証明の存在可能性を排除できるため, 実際に攻撃を提案することが大事です.

Boldyreva et al.(CCS 2007) では, M-LRSW問題が難しいということを仮定して, 高機能な署名方式の安全性証明を行っていました. ⁴ しかし, Hwang et al. (ASIACCS 2009) は, M-LRSW問題が簡単ということを示しています. Hwangらは証明方式自体への攻撃も行っています. ⁵ （この例はKoblitz and Menezes ⁶ から取りました.)

5. 証明が間違っていた

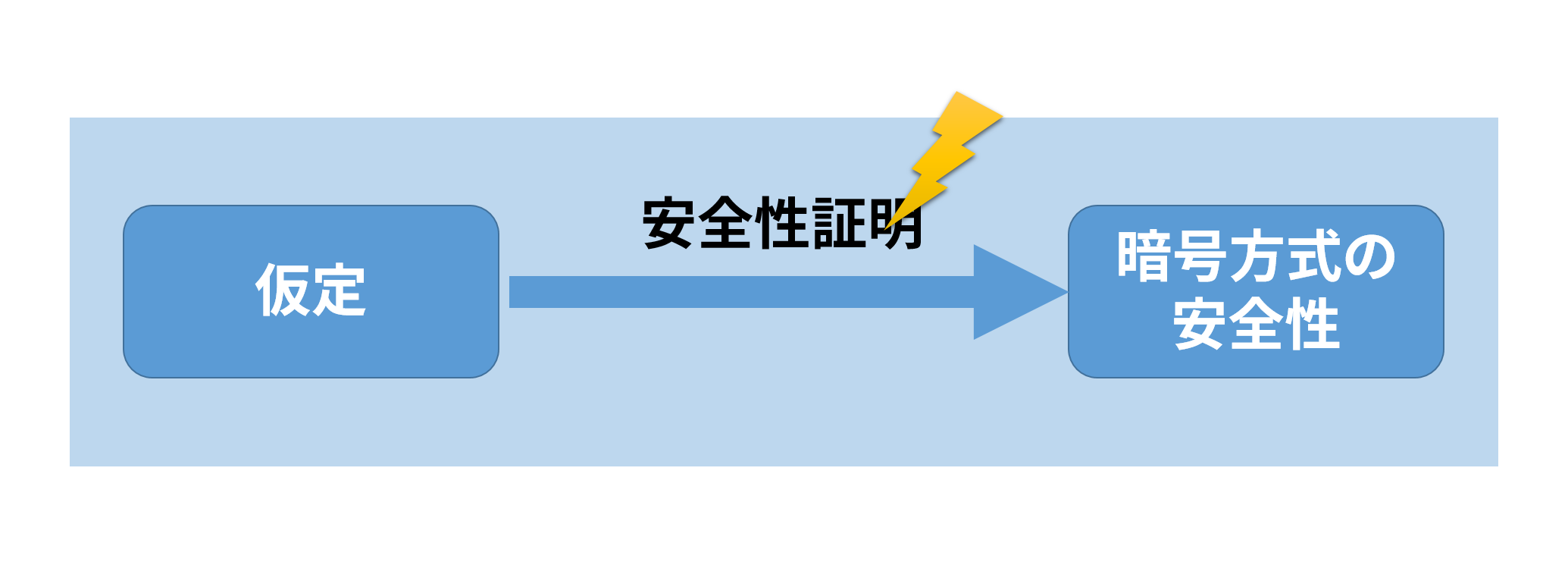
「安全性証明」に雷マークが付いています. 安全性証明を誤ることがあります. 「暗号技術Aまたは問題Aが難しいならば, 暗号方式Bは安全」という安全性定理の証明が間違っているケースを考えましょう. この場合, 「ある証明」が間違っていたのであって, 「別の証明」が付く可能性が残っています. 4の場合と同様に,　具体的に攻撃を行うことで, 別の証明の存在可能性を排除できるため, 実際に攻撃を提案することが大事です.

~~4の事例とちょっと近いのですが,~~ 最近のOCB2の事例がこれに当たります. P. Rogawayらが提案した認証暗号の一つにOCBがあります. OCB1, OCB2, OCB3の3バージョンが知られています. Rogawayが2004年に提案したものがOCB2として知られています. ⁷　InoueとMinematsu ⁸ が2018/10/26に論文をプレプリントサーバに投稿しました. この段階では, 偽造不可能性が破れていました.　また証明のどこが誤っているか, 方式を直すにはどうパッチを当てるかも議論されています. 更に2018/11/12には, Poettering ⁹ や Iwata ¹⁰ により秘匿性も破れることが分かりました.

6. 証明がなかった

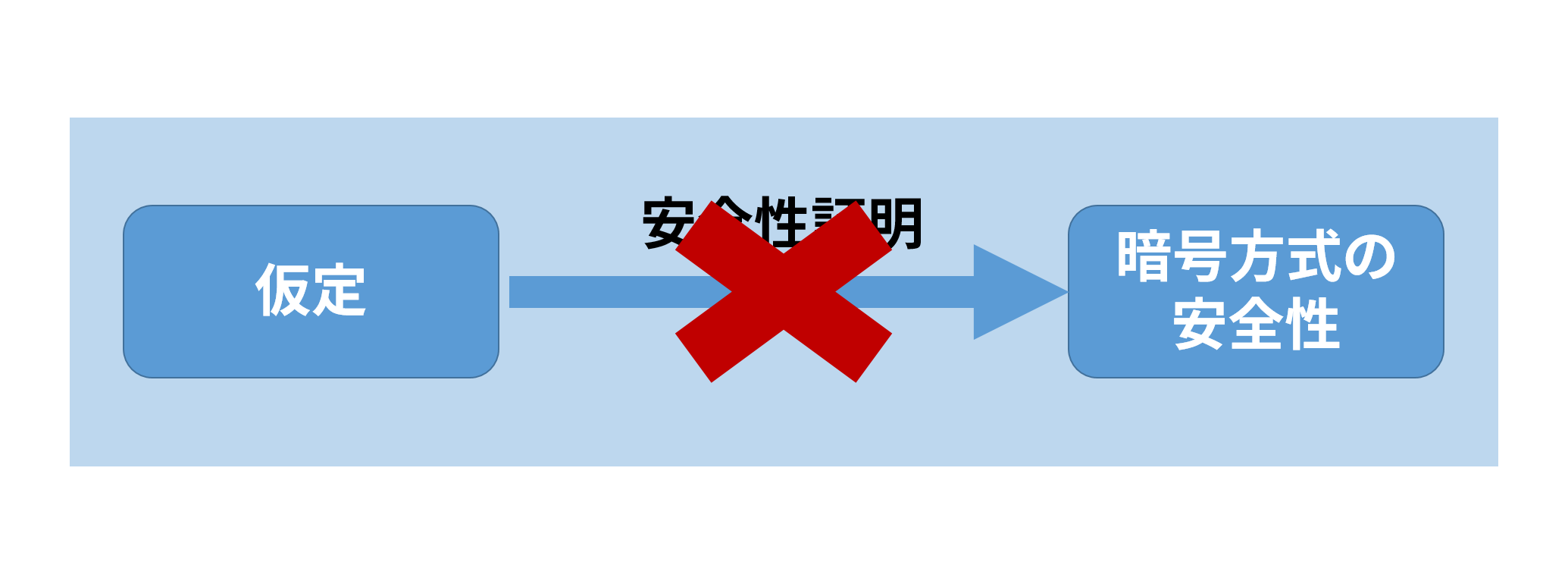
今度は「安全性証明」の矢印に×が付いています. てっきり安全性証明が付いていると思っていたら, 実はそんなことはなかったということがあります. ¹¹

このケースで有名なのはBellareとRogawayのOAEP ¹² でしょう.
論文の概要やイントロダクションには, F-OAEPは適切な仮定の下で選択暗号文攻撃の下で識別不可能 (IND-CCA2安全) と書かれています. 定理をよく読むと

Thm.5: Fが一方向性を持つ→F-OAEPはIND-CPA安全
Thm.6: F-OAEPはPA1安全

となっています.
よくよく読むと「公開鍵暗号方式AがPA1安全かつIND-CPA安全→AはIND-CCA安全」という定理はどこにもありません.

その後の研究 ¹³ で

「IND-CPA安全+PA1安全→IND-CCA安全」は言えない
「IND-CPA安全+PA2安全→IND-CCA安全」はOK

ということが分かりました. しかし, F-OAEPがPA2安全性を満たすかどうかはまだ分かりません. 最終的に, Shoup ¹⁴ により「Fが一方向性を持つ」という仮定だけでは不十分なことが示されました. 具体的には「Fが部分一方向性を持つ」という仮定が必要です.
幸い, FをRSAに限った場合については, 「RSAが一方向性を持つ→RSAが部分一方向性を持つ」ということがFujisaki, Okamoto, Pointcheval, and Stern ¹⁵によって示されています. よって「RSAが一方向性を持つ→RSA-OAEPがIND-CCA安全」が（Random Oracle Modelで）言えます。

まとめ

誰しも誤ることはある.

細かく言うと「難しい」や「安全」にも定義があります ↩
K. Akiyama, Y. Goto, S. Okumura, T. Takagi, K. Nuida, G. Hanaoka: A Public-Key Encryption Scheme Based on Non-linear Indeterminate Equations (SAC 2017). https://link.springer.com/chapter/10.1007%2F978-3-319-72565-9_11 ↩
K. Xagawa: Practical Cryptanalysis of a Public-key Encryption Scheme Based on Non-linear Indeterminate Equations at SAC 2017 (PQCrypto 2018). https://link.springer.com/chapter/10.1007/978-3-319-79063-3_7 や https://eprint.iacr.org/2017/1224 ↩
A. Boldyreva, C. Gentry, A. O’Neill, and D. H. Yum: Ordered multisignatures and identity-based sequential aggregate signatures, with applications to secure routing. (CCS 2007) https://eprint.iacr.org/2007/438. ↩
J. Y. Hwang, D. H. Lee, and M. Yung: Universal forgery of the Identity-Based Sequential Aggregate Signature Scheme (ASIACCS 2009) ↩
Neal Koblitz and Alfred Menezes: The brave new world of bodacious assumptions in cryptography. (Notices of the AMS, 57 (2010), 357-365). http://cacr.uwaterloo.ca/~ajmeneze/anotherlook/ams2.shtml ↩
P. Rogaway: Efficient Instantiations of Tweakable Blockciphers and Refinements to Modes OCB and PMAC. (ASIACRYPT 2004) ↩
Akiko Inoue and Kazuhiko Minematsu: Cryptanalysis of OCB2 (Cryptology ePrint Archive: Report 2018/1040) https://eprint.iacr.org/2018/1040 ↩
Bertram Poettering: Breaking the confidentiality of OCB2 (Cryptology ePrint Archive: Report 2018/1087) https://eprint.iacr.org/2018/1087 ↩
Tetsu Iwata: Plaintext Recovery Attack of OCB2 (Cryptology ePrint Archive: Report 2018/1090) https://eprint.iacr.org/2018/1090) ↩
安全性証明がない方式は沢山あります. ↩
Bellare and Rogaway: Optimal asymmetric encryption -- How to encrypt with RSA (EUROCRYPT 1994). Bellare - OAEPから完全版にアクセス可能 ↩
M. Bellare, A. Desai, D. Pointcheval and P. Rogaway: Relations among notions of security for public-key encryption schemes (CRYPTO 1998). Bellare - BDPR98から完全版にアクセス可能 ↩
V. Shoup: OAEP Reconsidered (CRYPTO 2001, JoC 2002). http://eprint.iacr.org/2000/060 ↩
E. Fujisaki, T. Okamoto, D. Pointcheval, J. Stern: RSA-OAEP Is Secure under the RSA Assumption (CRYPTO 2001, JoC 2004). http://eprint.iacr.org/2000/061 ↩