はじめに
この記事はReinforcement Learning: An Introduction(Sutton本)の個人的なまとめと理解が難しかった所をメモしているだけの記事です。
強化学習を勉強中の人が書いただけの記事なので間違っている所もあると思います。気づいたら是非コメントしていただけたらと思います。
記載範囲
2章全部
内容
k-armed bandit問題を扱って、”行動状態価値”と”探索と活用”に対していくつかのアルゴリズムを提案する。
行動状態価値の推定
定常状態の時
最もシンプルな推定は
$$Q_t(a) = \frac{1}{N(a)}[R_1+R_2+\dots+ R_{N(a)}]$$
$a$の腕を選んだ時に受け取った報酬$R$の履歴の平均を取る最も直感的な推定方法。
実際に計算する際にはすべての報酬履歴を取っておくのはメモリ的に大変なので
$$Q(a) \leftarrow Q(a) + \frac{1}{N(a)}[R-Q(a)]$$
として今の行動価値の推定値$Q(a)$と$a$のうでが選ばれた回数$N(a)$だけを保持して更新していく。
非定常状態の時
先程の単純平均だと全ての報酬が同じ重みで評価されるので非定常状態の推定には向かない
ここで
\begin{align}
Q_{n+1}(a) &= Q_n(a) + \alpha[R_n-Q_n(a)] \\
\\
(&= \alpha R_n + (1-\alpha)\alpha R_{n-1} + \dots + (1-\alpha)^{n-1}\alpha R_1 + (1-\alpha)^nQ_1) \tag{1}
\end{align}
のように更新すると直近がより重視され昔の報酬は軽視される。
問題として収束する為の理論的条件を満たしていない
条件は以下
\sum^{\infty}_{n=1}\alpha_n(a)=\infty, \qquad \sum^{\infty}_{n=1}\alpha^2_n(a)<\infty
ただし、実務上はあまり気にする必要はなくむしろ条件を満たすものは収束が遅かったりするらしい。
もう一点細かい問題として初期値$Q_1$がずっと残ってしまう点である(ステップ数が増えれば実務上は問題ないレベルになるが)
これを解決する為に$Exercise 2.7$で解決策が提案されている。
Exercise 2.7
今まで議論していたステップパラメーター$\alpha$を
\beta_n \doteq \alpha / \bar{o}_n \\
\bar{o}_n \doteq \bar{o}_{n-1} + \alpha(1 - \bar{o}_{n-1}) \quad (\bar{o}_0 \doteq 0)
とする。
$\alpha$が重複しているので分かりにくいが要は
$$ Q_{n+1}(a) = Q_n(a) + \beta_n[R_n-Q_n(a)] $$
と更新する事になる
展開すると
\begin{align}
Q_{n+1} &= Q_n + \beta_n[R_n - Q_n]\\
&= \beta_nR_n + (1-\beta_n)Q_n \\
&= \beta_nR_n + (1-\beta_n)( Q_{n-1} + \beta_{n-1}(R_{n-1} + Q_{n-1}))\\
&= \cdots \\
&= \beta_nR_n + (1-\beta_n)\beta_{n-1}R_{n-1} + \cdots + (1-\beta_n)(1-\beta_{n-1})\cdots(1-\beta_2)\beta_1 R_1 + \\
& \qquad (1-\beta_n)(1-\beta_{n-1})\cdots(1-\beta_2)(1-\beta_1) Q_1 \tag{2}
\end{align}
ここで$\bar{o}_1$は
\begin{align}
\bar{o}_{1} &= \bar{o}_{0} + \alpha(1 - \bar{o}_{0})\\
&= 0 + \alpha (1-0) \\
&=\alpha
\end{align}
より
$$ \beta_1 = \alpha / \bar{o}_{1} = 1 $$
となる。
$(2)$の最後の項には$(1-\beta_1)$が存在するので結果として最後の項が0になり、初期値のバイアスが考慮されない非定常パラメーターを作る事ができた。
(実際にはそれほど初期値が邪魔する事ない気もしますし、計算もめんどくさそうなので使う事はなさそうです。)
Gradient Bandit Algorithms
(行動価値の推定の項に書きましたが、探索アルゴリズムでもあると思います。)
深層学習の確率勾配法を使った手法で、行動価値$Q$を直接推定する訳ではなく$H(a)$という腕$a$を選ぶ傾向のようなものを更新する方策関数$\pi(a)$を定義している
\pi(a) \doteq \frac{e^{H(a)}}{\sum^k_{b=1}e^{H(b)}}
いわゆるSoftmax関数。
更新式は
H_{t+1}(A_t) \doteq H_t(A_t) + \alpha (R_t - \bar{R}_t)(1-\pi_t(A_t)) \qquad\\
H_{t+1}(A_t) \doteq H_t(a) - \alpha (R_t - \bar{R}_t)\pi_t(a) \qquad(a \neq A_t)
右の項が報酬の勾配に相当する部分。原著にかなり丁寧に書かれているので詳しい事は割愛
ポイントとしては選ばれた腕は関係なく全ての$H$が更新される点。
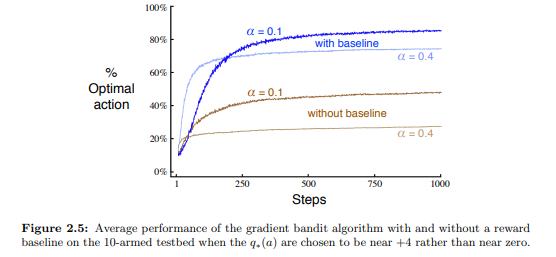
また$\bar{R}$は$baseline$とよばれここでは報酬の平均を取っているが、何にしても問題はない。
ただし問題ないというのは期待値に影響を与えないという意味で、分散に影響を与えるらしく適切に与えないと収束が遅くなるらしい。
たしかに遅い。
探索アルゴリズム
ε-greedy
最もオーソドックスな手法
小さめな$\varepsilon$をとって$\varepsilon$の確率で腕を選択して$1-\varepsilon$の確率でgreedyに行動を決定する。
UCB
理論的な期待値や分散との誤差を検討する事で探索と活用を両立したやり方。
突然UCBの式がでてくるのでわからない人は多腕バンディット問題におけるUCB方策を理解するなどを参考にすると理解しやすいと思います。
式は以下
$$ A_t \doteq \arg \max_a\Bigg[Q_t(a) + c\sqrt{\frac{\ln t}{N_t(a)}}\Bigg]$$
左項$Q_t(a)$はその時点での各腕の期待報酬であり、右項はどれだけ探索できているか(今の推定値がどれだけ正確か)を図る値である
($t$はぜんざいが現在のステップ数であり$N(a)$は腕$a$が何回選ばれたかを示す。$c$はハイパラ)
最適初期値
他とは少し議論が変わるが初期値を最適化して上手い事探索していこうという考え。
- greedyな方策で初期値を全て5
- $\varepsilon$-greedyで初期値を全て0
の二つの手法を比べてみると以下の様なグラフになる
(10-armed testbedで真の行動価値は平均0分散1で生成された)
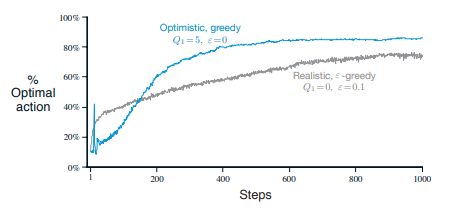
greedyな手法のほうが強い事が分かる。
理由として、最初に十分大きい初期値を持つと行動が採用されて行動価値が十分に下方修正されていない限りは過大評価されていることになり、結果として、greedyに行動しても結果として十分に探索できることになるため。
恐らく期待報酬が最大の腕以外はほとんどすべてが過大評価される状態になっているが最大のみが知りたい場合はランダムで行動するよりも効率よく探索ができる事が多い。
まとめ
いくつかのアルゴリズムが提案されたが実際にどれが一番良いかは解きたいタスクやパラメーターなどに依存する為簡単には言えない。
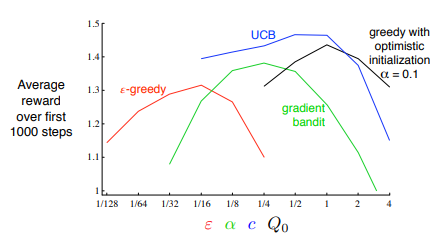
原著では提案手法の差分をグラフにしている
ここではUCBが一番いいという結果である。(初期値最適化も強い)