歩行安定化制御についての勉強メモ

歩行安定化制御についての勉強メモ

不勉強で解説できるほどではないが、歩行安定化制御についての勉強メモを共有する。大目にみてください。あくまで自分の理解で、もし間違ったらコメントよろしくお願いします。

概要

歩行ロボットが歩行するときに、地面の凸凹(または測定した地面の高さとの誤差)やサーボ制御誤差、機械的な幾何誤差の影響により、歩行パターン生成プログラムで生成された軌道をそのまま再生すると大体コケる。これらの誤差を吸収するため第二のソフトウェア"スタビライザー"が必要。状況に応じてリアルタイムで姿勢回復するような一連の歩行動作を生成するスタビライザーも存在するが、この記事は目標値の近辺に微修正をかけるだけのスタビライザーを対象にする。また実装例としてhrpsys-baseのStabilizerを拝借した(choreonoidのライブラリで書き換えた)。これについても説明する。

安定化制御の例

安定化制御とは、

• 着地時に足のばたつきをいち早く抑える
• 目標姿勢を保たせる

ように働いている。

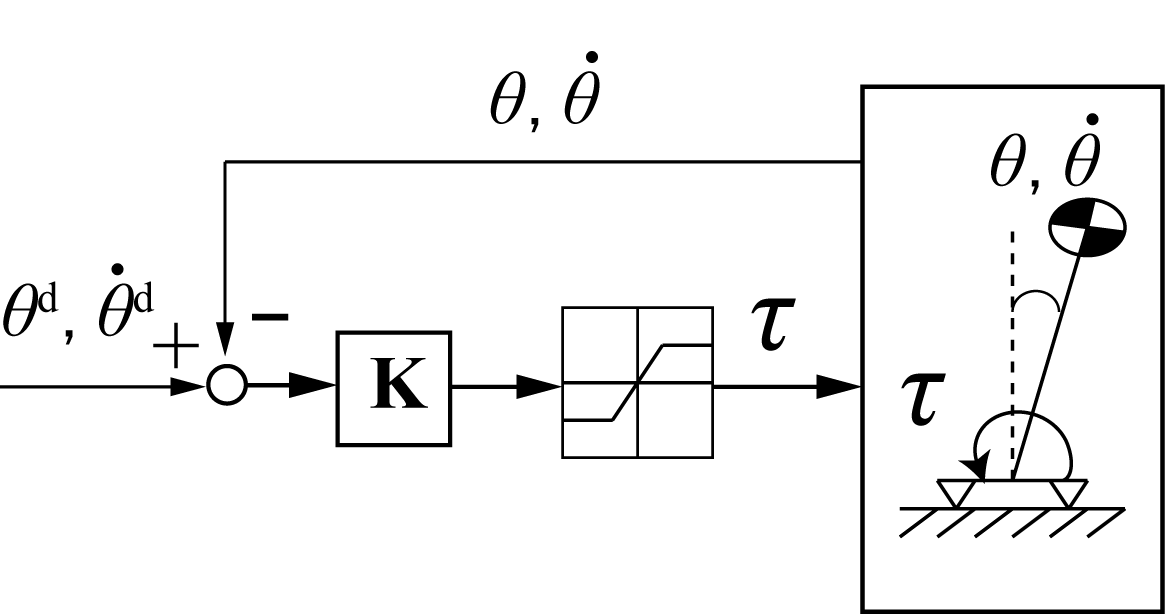
ではまずロボットを倒立振子モデル化して見てみよう。以下は一番簡単なSTの例。これは単純に姿勢をPD制御で足首トルクに変換する制御だが、この制御だと現在の足首トルクが見ていないため、足首トルク出力の$\tau$が振動になりやすくて、素早く目標値への収束が難しい。

\tau = k_1(\theta ^d - \theta) + k_2(\dot{\theta}^d - \dot{\theta})

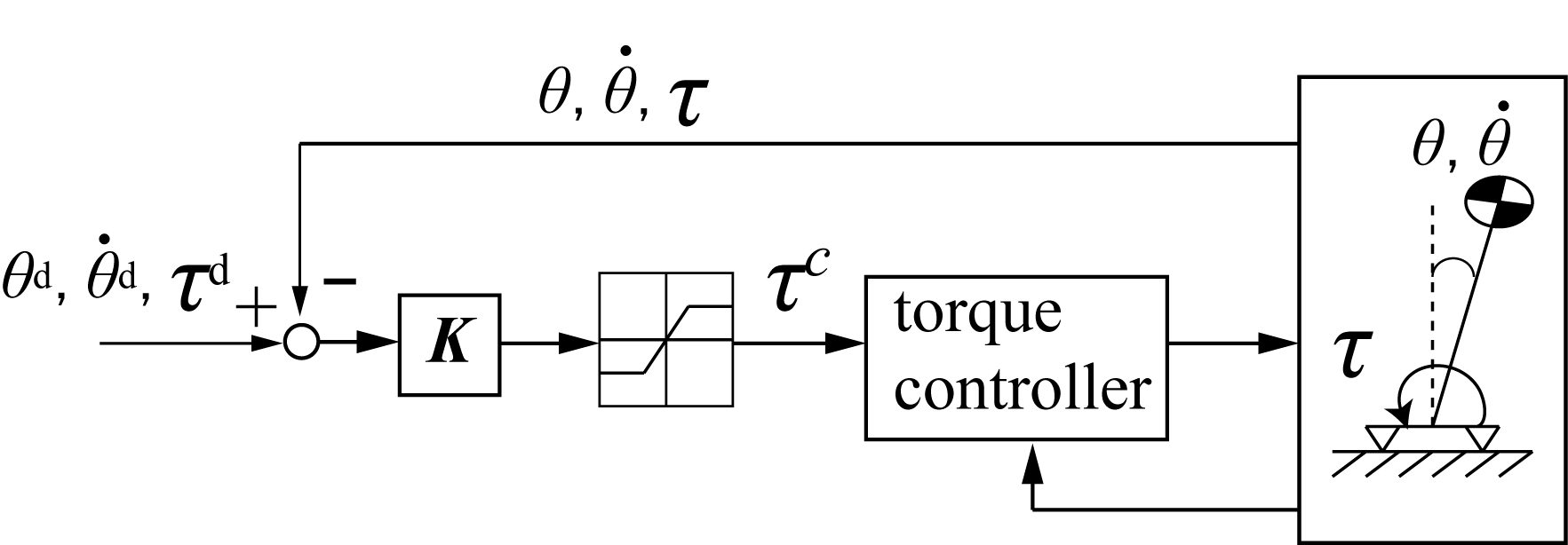
次に少し改良したSTの例。こっちは足首に力センサを設置し、床反力を測定している。床反力は直接にロボットの姿勢を影響するため、床反力をうまく制御すればロボットの姿勢を安定化させることができる。

\tau ^c = k_1(\theta ^d - \theta) + k_2(\dot{\theta}^d - \dot{\theta}) + k_3(\tau ^d - \tau)

次は以下2種類の倒立振子モデル見てみよう。一個目は入力がトルクのトルク制御型。

\ddot {x} = \displaystyle \frac{g}{z _z} + \frac{1}{Mz_c} \tau

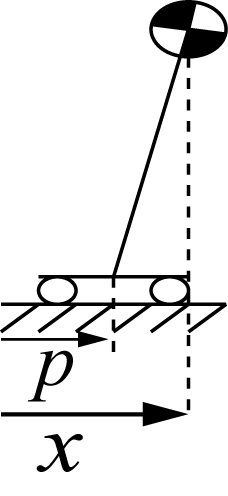
二個目は入力がzmpのzmp制御型。

\ddot {x} = \displaystyle \frac{g}{z _z}(x-p)

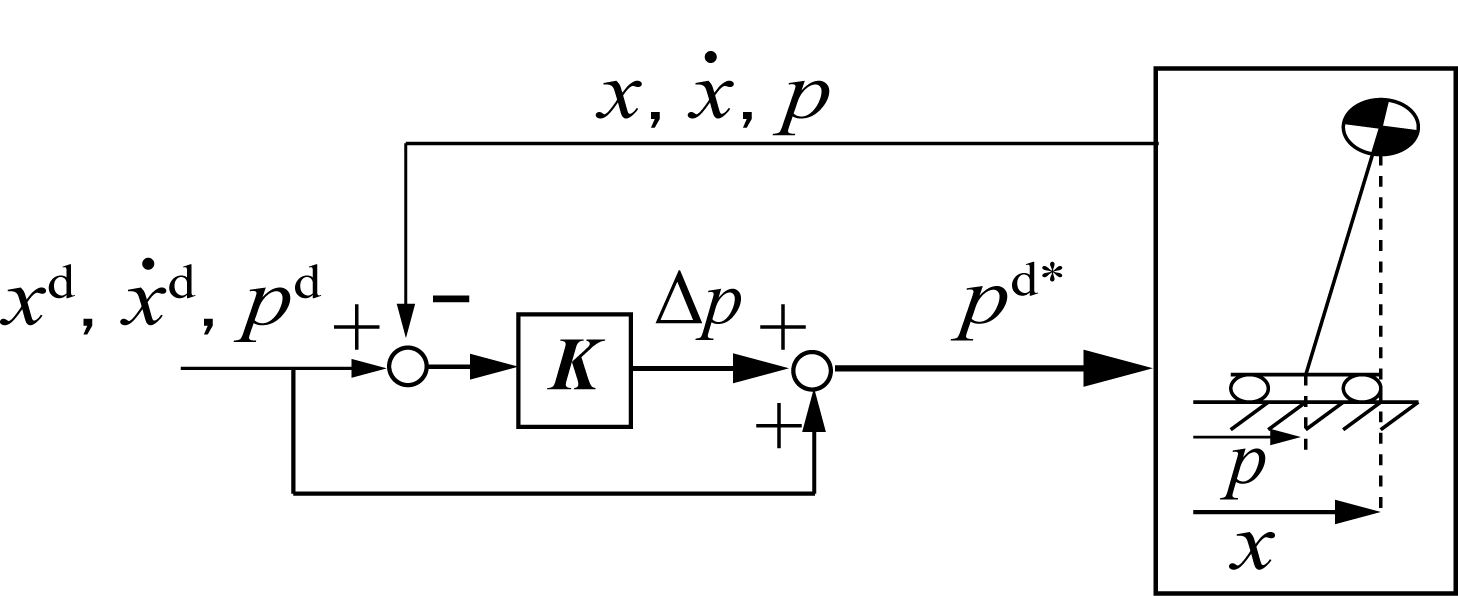
zmpが床反力の情報を持っているので、トルク制御型の倒立振子と同じ制御系の構築も可能と考える。また、位置制御ベースのロボットだとzmp制御型の方が適用しやすいメリッドがある。以下にzmp制御型の倒立振子安定化制御の図を示す。

なお、機械のコンプライアンス要素やモーター制御の遅れの影響により実zmpと目標zmpと比べて常に遅れている。この図の${\it p}^{\rm d}$を一次遅れ要素$\displaystyle \frac{1}{1+ sT_p}$かけることでこの現象をモデル化する。

p = \displaystyle \frac{1}{1+sT_p}p^d

この制御系の状態${\boldsymbol x} \equiv \begin{bmatrix} x & \dot x & p \end{bmatrix} ^ {\rm T}$とおいて、状態方程式が以下の通り：

{\dot {\boldsymbol x}} = {\bf A}{\boldsymbol x} + {\boldsymbol B}u \\
{\bf A} \equiv \begin{bmatrix} 0 & 1 & 0 \\ g/z_c & 0 & -g/z_c \\ 0 & 0 & -1/T_p \end{bmatrix} \\
{\boldsymbol B} \equiv \begin{bmatrix} 0 & 0 & 1/T_p \end{bmatrix} ^ {\rm T} \\
u = {\boldsymbol K}({\boldsymbol x} ^d - {\boldsymbol x}) + p^d

ここでfeedback gain ${\boldsymbol K}=\begin{bmatrix}k_1 & k_2 & k_3 \end{bmatrix} $は極配置で決めればよい。杉原先生の論文によると極の一つを$- \sqrt{g/z_c} $($g$=重力, $z_c$=重心高さ)に配置すると最良のレギュレータになる。もっと詳しい話知りたい方、杉原先生の論文"Standing Stabilizability and Stepping Maneuver of Bipeds based on the Best COM-ZMP Regulator"と梶田さんの論文"Biped Walking Stabilization Based on Linear Inverted Pendulum Tracking"を参照されたい。STのこの部分は倒立振子トラッキング制御と呼ぶ！
梶田さんの論文にしたがって極を$(-13, -3, -\sqrt{9.8/z_c})$と設定し、以下のscilabノートで一瞬で ${\boldsymbol K}$を解ける。

z=0.804992 //重心高さ
T=0.04 //目標zmpを一次遅れさせる時定数
A=[0 1 0;9.8/z 0 9.8/-z;0 0 -1/T]
B=[0;0;1/T] 
K=ppol(A,B,[-13,-3,-sqrt(9.8/z)]) 

歩行安定化制御の実装

hrpsys-baseのStabilizerを拝借してOpenHRP3ライブラリに依存する部分をchoreonoidのライブラリで書き換えた。制御則は特にいじっていない。
choreonoidライブラリで書き換えたソース
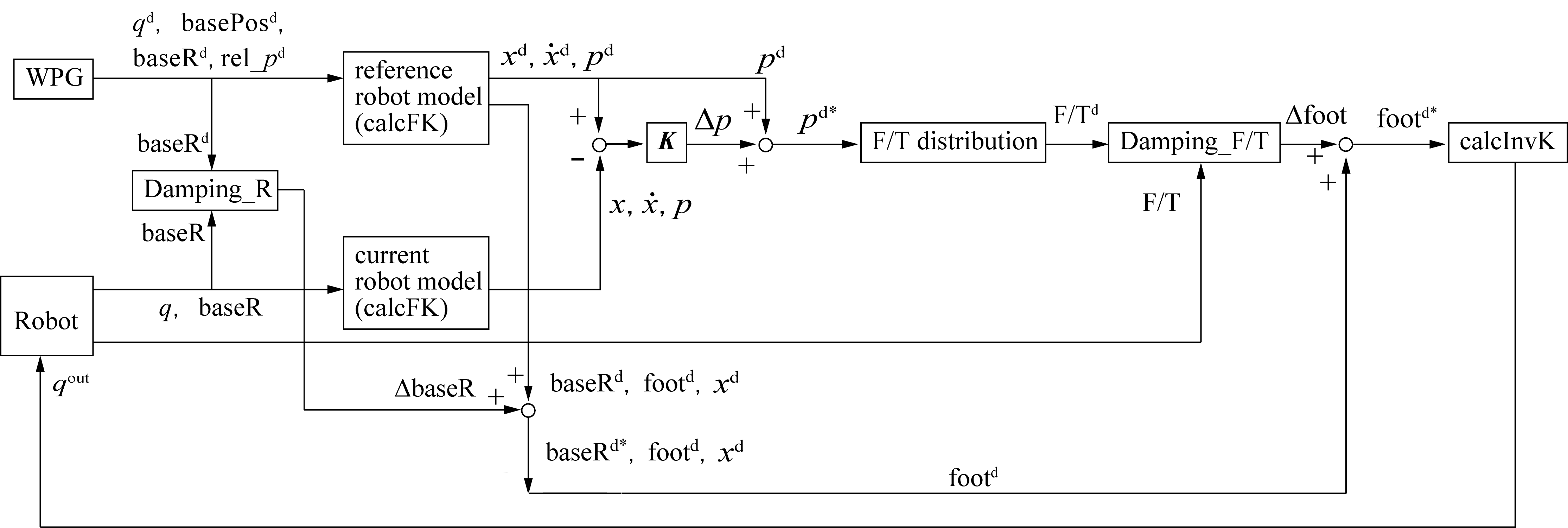
ソースコードを読んで自分の理解だとこの安定化制御則を以下の図でまとめた(あくまで自分の理解)：

この図の変数の定義は以下の通り：

• WPG: 歩行パターン生成
• $q$: 関節角度
• F/T: 床反力
• foot: 足位置姿勢
• basePos: 腰リンク位置
• baseR: 腰リンク姿勢
• rel_$p^d$: 腰リンク座標系(ロボット座標系から見た目標zmp)
• 上付きd: 目標値
• 上付きd*: 修正後の目標値

damping制御

安定化制御の腰の姿勢と足の反力制御にdamping制御を用いた。詳細は梶田さんの論文を参照されたい。簡単に説明すると、PD制御ライクだが、出力が"修正量"で、この修正量は時定数で減衰する。damping制御は以下の式で表す：

\dot \delta = D^{-1}(\tau ^d - \tau) - \displaystyle \frac{1}{T_c}\delta

実装上用いる離散化した式は以下の通り：

\delta[k+1] = (D^{-1} (\tau ^d[k] - \tau [k]) - \displaystyle \frac{1}{T_c} \delta[k])dt + \delta[k]

ここでの変数定義は以下の通り：

• $\tau ^d$: 目標値
• $\tau $: 現在地
• $\delta$: 修正量
• $T_c$: 時定数
• $D$: damping係数。小さいほど反応が早い。STのゲイン調整に苦労したパラメータ。
• $dt$: 制御周期

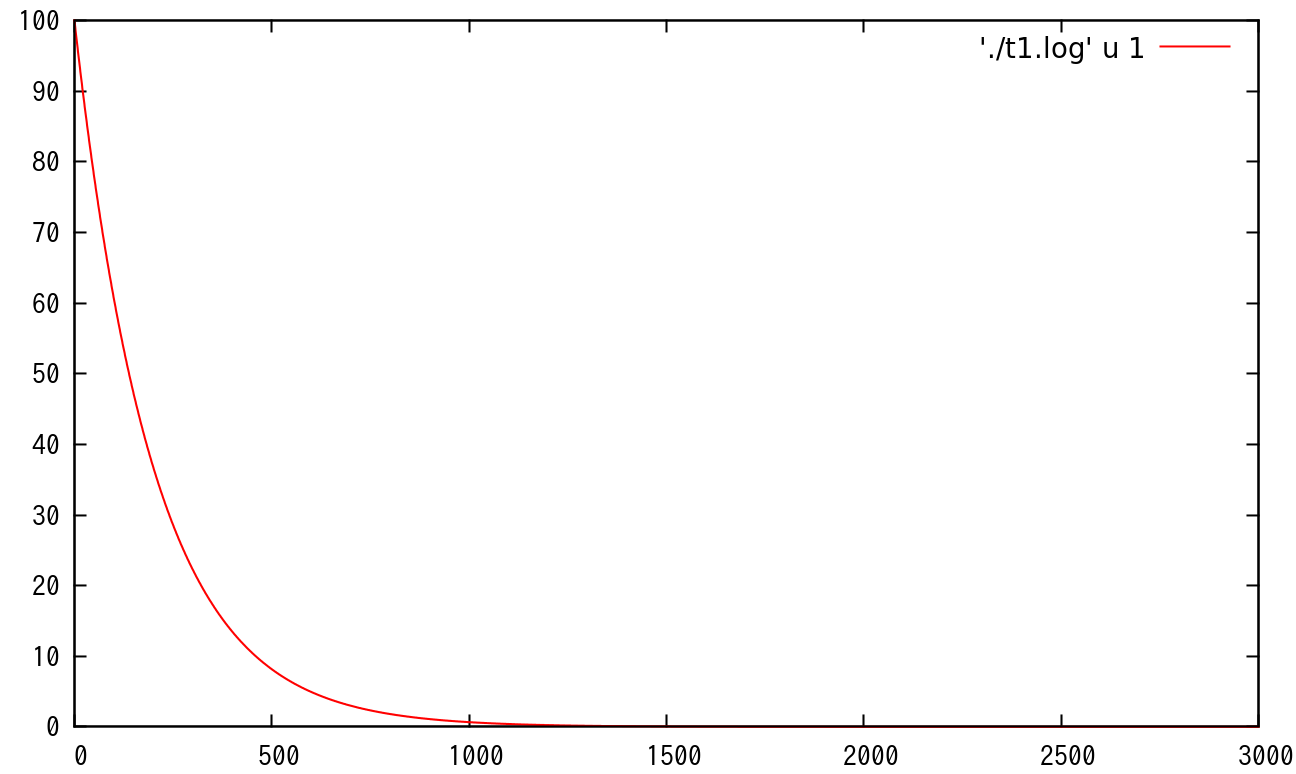
修正量減衰の一例を以下の図に示す。この例は$\tau ^d[k] = \tau [k]$の時、$T_c = 1$、修正量初期値=100の例である。修正量が0になったらニュートラル位置に戻る。

まとめ。梶田さんの論文だとSTはこの３つの要素をいじるだけ：

• waistの姿勢
• 両足の姿勢
• 両足の高度差

だが、hrpsys-baseの実装読んでみると両足のx、y方向の補正もされている。必要あるのかな...

StabilizerのRTCの使い方：

自分の使い方をここで共有する。実際にSTを扱うところはpythonスクリプトを参照されたい。

data port関連

• inportに入力する情報
  • rpy: カルマンフィルタ出したrpy測定値
  • rfsensor: ロボットの右足6軸力センサ値
  • lfsensor: ロボットの左足6軸力センサ値
  • qCurrent: ロボットの現在角度
  • qRef: 角度指令値
  • zmpRef: ロボット座標系から見た目標ZMP
  • basePosIn: 目標ロボット座標系位置
  • baseRpyIn: 目標ロボット座標系姿勢
  • contactStates: 二足の場合長さ2のデータ。それぞれ右足、左足の接地状態を表す。空中にある場合は0で、それ以外の場合は1。
  • toheelRatio: 二足の場合長さ2のデータ。それぞれ右足、左足の足の回転状態を表す。つま先かかと接地期の足には0，それ以外の場合は１。
  • controlSwingSupportTime: 二足の場合長さ2のデータ。それぞれ右足、左足の支持脚->遊脚もしくは遊脚->支持脚 のように接地状態が変わるまでの時間。
• outport
  • q: STが修正後の関節角度指令値。これをサーボに入力

パラメータ設定

パラメータの設定は、STのサービスポートのgetParameter()メソッドにて一度現在のすべてのパラメータを構造体として取得し、弄りたい部分を値で代入してから再度セットするやり方で行う。自分は以下のパラメータを設定した：

• eefm_leg_inside_margin: 足首位置から足の支持多角形の内側エッジまでの距離
• eefm_leg_outside_margin: 足首位置から足の支持多角形の外側エッジまでの距離
• eefm_leg_front_margin: 足首位置から足の支持多角形の前方エッジまでの距離
• eefm_leg_rear_margin: 足首位置から足の支持多角形の後方エッジまでの距離
• eefm_k1: 前述した倒立振子トラッキングfeed backのゲイン $k_1$
• eefm_k2: 前述した倒立振子トラッキングfeed backのゲイン $k_2$
• eefm_k3: 前述した倒立振子トラッキングfeed backのゲイン $k_3$
• eefm_rot_damping_gain: rpy3自由度の足姿勢damping制御係数。長さは3*手足数
• eefm_pos_damping_gain: xyz3自由度の足位置damping制御係数。長さは3*手足数
• stp_org.st_algorithm: STのアルゴリズム種類。OpenHRP.StabilizerService.EEFMQPCOPで良いらしい。

自分が使用する最低限のサービスポートメソッド

• getParameter(): 安定化制御のすべてのパラメータを構造体として取得
• setParameter(): 安定化制御のすべてのパラメータを構造体で渡して設定
• startStabilizer(): 安定化制御開始
• stopStabilizer(): 安定化制御オフにする。

全部のメソッドを知りたい方はstabilizerのidlを参照されたい。
これで一旦区切ってアップする。

次回を待て！！