ワイルドカードと正規表現はどちらも検索や置換でよく使われている馴染みのある形式言語です。
ワイルドカードは正規表現より弱い(表現力低い)ことが知られています。下図のように完全包含関係です。
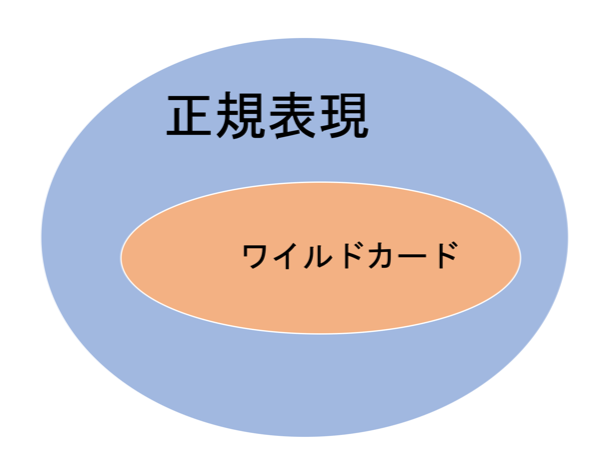
実装難易度と応用場面の広さのトレードオフになりますが、どちらでもよく使われています。
ワイルドカード実用例 (shellでのファイルマッチング)
ls *.log
正規表現の実用例 (メールアドレス Python from here )
r"(^[a-zA-Z0-9_.+-]+@[a-zA-Z0-9-]+\.[a-zA-Z0-9-.]+$)"
今回は簡単なほうのワイルドカードのマッチング判定ロジックisMatch()を自分の手で実装してみました。
サポートするパターン記号は (簡単な実装なので、Unicode対応やエスケープ対応などは不要)
-
?任意の1文字(char)とマッチ -
*任意長さ(0も含む)の文字列(string)とマッチ -
その他文字そのまま(文面)とマッチ
例
- 文字列
"aa"パターン"?a"結果: ⭕ マッチ - 文字列
"aa"パターン"*"結果: ⭕マッチ - 空文字列
""パターン"**"結果: ⭕マッチ - 文字列
"aa"パターン"a"結果: ❌アンマッチ - 文字列
"aa"パターン"b*"結果: ❌ アンマッチ
厳密の問題定義は以下にもご参考ください。
(コード提出可能なので、回答を見る前にまずチャレンジしてみたほうが良い)
LeetCode
GeeksForGeeks
TL;DR
最近Goでアルゴリズムを書くのに嵌っています。Goで実装を書いてみました。
問題全体的な思考
*を考慮しなければ、マッチした文字列とパターンは長さが一致するはずです。
そして、両者はきれいに1文字対1文字で単純にチェックすれば解決です。
*の効果を含めて考えれば、文字列とパターンのマッチングの場所は不確定になり、マッチング対応関係が何通りもできる場合もあります。
以下の例には、文字列s=aabb、パターンp=*a*b*のマッチング対応は4通りあります。
(対応関係を表すために空白を入れています。スペース文字と関係はありません。)
s: a a b b
p: * a * b *
p: * a * b *
p: * a*b *
p: * a * b *
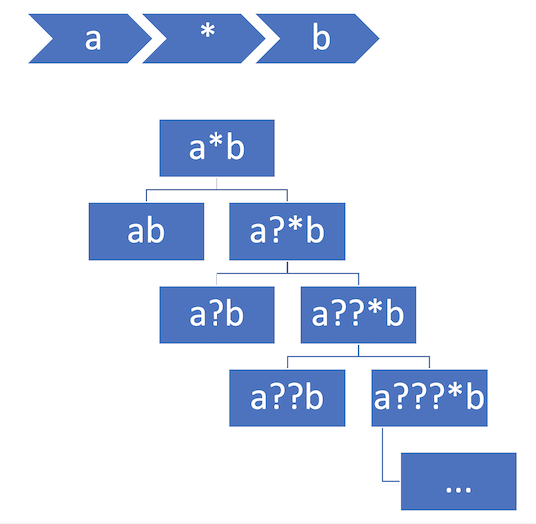
実装方法1 (再帰を使って深さ優先探索)
まずは愚直的に再帰で実装してみました。
以下の例はa*b => ab a?b a??b a???b ...の展開を示す分岐ツリーです。
-
*が0文字とマッチする (↑のツリー図では、左に行く)場合 -
*が1以上の文字とマッチする(↑のツリー図では、右に行く)場合
2.の場合なら、再帰で判断します。
実装コードは以下になります。
func isMatch(s string, p string) bool {
for p != "" {
if p[0] == '*' {
// case when * matches 0 charactor
if isMatch(s, p[1:]) {
return true
}
// case when * matches 1 or more charactor
if s == "" {
return false
}
s = s[1:]
continue
}
if s == "" || p[0] != '?' && p[0] != s[0] {
return false
}
p, s = p[1:], s[1:]
}
// when p == ""
return s == ""
}
簡単なインプットで試して、予想通りな結果が出ましたが、LeetCodeに提出したら、性能悪すぎて、TimeLimitExceedになりました。
最初に落ちたケースは以下です。
s="bbbababbbbabbbbababbaaabbaababbbaabbbaaaabbbaaaabb"
p="*b********bb*b*bbbbb*ba"
ワイルドカードの定義から見ると、連続のアスター********は、意味上は1個の*と一緒ですね。
複数の連続*を1個にまとめる事前処理を入れてみました。
import "strings"
func simplify(p string) string {
var sb strings.Builder
isLastStar := false
for _, ch := range p {
if ch == '*' {
if isLastStar {
continue
}
isLastStar = true
} else {
isLastStar = false
}
sb.WriteRune(ch)
}
return sb.String()
}
func isMatchHelper(s string, p string) bool {
// もともとのisMatchの実装
}
func isMatch(s string, p string) bool {
return isMatchHelper(s, simplify(p))
}
結果は、もっと多くのケースが通りましたが、まだTLE(Time Limit Exceeded)エラーですべて通らなかったです。
今回は最初に落ちたケースは以下です。
s="abbabaaabbabbaababbabbbbbabbbabbbabaaaaababababbbabababaabbababaabbbbbbaaaabababbbaabbbbaabbbbababababbaabbaababaabbbababababbbbaaabbbbbabaaaabbababbbbaababaabbababbbbbababbbabaaaaaaaabbbbbaabaaababaaaabb"
p="**aa*****ba*a*bb**aa*ab****a*aaaaaa***a*aaaa**bbabb*b*b**aaaaaaaaa*a********ba*bbb***a*ba*bb*bb**a*b*bb"
simplified_p="*aa*ba*a*bb*aa*ab*a*aaaaaa*a*aaaa*bbabb*b*b*aaaaaaaaa*a*ba*bbb*a*ba*bb*bb*a*b*bb"
ローカルで試しても、おおよそ7グループ以上の*が存在すれば、1秒〜無限長がかかってしまいました。
やはり、大きいインプットに対して再帰での実装が無力でした。
次はDPで書き直してみました。
実装方法2 (DP 動的計画法)
2次元の計算表dpt[len(s)+1][len(p)+1]を順番に埋めていく手順を踏まえて、1マスを定数時間で計算できれば、全体的にO (len(s+1) * len(p+1))の計算量(時間も空間も)で解けますね。
dpt[i][j]はBoolean値で、その意味を「小規模のサブ問題s[0:i]とp[0:j]がマッチするか」とします。
まずは、些細なケースから埋めていきます。
明らかに、空文字と空パターンがマッチするので、dpt[0][0] = true
空ではない文字と空パターンが絶対マッチしないので、dpt[i][0] = false, 1 <= i <= len(s)
そして、空文字とパターンp[0:j]のマッチング結果は、パターン最後の文字p[j-1]が*かどうかで判断します。
このDPの遷移ルールは以下となります。
// 1 <= j <= len(p)
dpt[0][j] = dpt[0][j] = dpt[0][j-1] // when p[j-1] == "*"
dpt[0][j] = false // otherwise
実装コードは以下です。
func isMatchDP(s string, p string) bool {
dpt := make([][]bool, len(s)+1)
for i := range dpt {
dpt[i] = make([]bool, len(p)+1)
}
dpt[0][0] = true
for j := 1; j <= len(p); j++ {
if p[j-1] == '*' {
dpt[0][j] = dpt[0][j-1]
}
}
for i := 1; i <= len(s); i++ {
for j := 1; j <= len(p); j++ {
switch p[j-1] {
case '?':
fallthrough
case s[i-1]:
dpt[i][j] = dpt[i-1][j-1]
case '*':
dpt[i][j] = dpt[i-1][j] || dpt[i][j-1]
default:
dpt[i][j] = false
}
}
}
return dpt[len(s)][len(p)]
}
dptを埋めていく中で、当行は1行前まで参照するので、メモリ上は常に当行と前行の2行のみ保持しても問題ありません。
そうすると、空間計算量 O(len(p))まで削減できます。
もっと最適化すると、空間計算量定数O(1)のやり方もあります。
実装方法3 (4つのポインタ)
文字列sとパターンpそれぞれの現在処理位置のポインタiとj以外に、もう2つのポインタasterIとasterJを使うことによって、定数空間計算量での実装が可能です。
アルゴリズム概要は以下です。
-
asterIは現在処理中のsの中の*にマッチする最新の場所を指します。
asterJは現在処理中のpの中の*を指します。 -
*ではない場合は、単純比較で、マッチしたらポインタiとjともに次に移動します。 -
*の場合、asterIとasterJを現在の場所に移動します。 -
*ではないし単純比較もマッチしない場合は、iとjをそれぞれasterIとasterJの次の場所に移動します。
ソースは以下になります。
func isMatchConstSpace(s string, p string) bool {
if p == "" {
return s == ""
}
var i, j = 0, 0
var asterI, asterJ = -1, -1
for i < len(s) {
if j < len(p) && (p[j] == '?' || s[i] == p[j]) {
i++
j++
} else if j < len(p) && p[j] == '*' {
asterI, asterJ = i, j
j++
} else if asterJ != -1 {
i, j = asterI+1, asterJ+1
asterI++
} else {
return false
}
}
for ; j < len(p); j++ {
if p[j] != '*' {
return false
}
}
return true
}
参考元は ここ ですが、この記事最後に、時間計算量は線形O(len(p))と書いてありますが、実はi,jポインタの移動は単一方向ではなく、往復があるので、最悪の場合はO(len(s)*len(p))でしょうね。
確かに、補助のメモリを使っていないので、空間計算量は定数です。
本当に思いつきにくい方法でした。(^o^;)