概要

微分、偏微分、全微分のあたりを説明したから次は座標変換だろう。記事が長くなったため前半後半に分けた。

後半『数学勉強ノート（座標変換と体積素・微分形式）〜〜関数解析、多様体、解析力学への準備〜〜(未公開)』

またこの記事は前回までの記事の内容を理解している前提で話が進む。必要に応じて前回までの記事を参照するとより理解が深まることと思う。

前々回『数学勉強ノート（微分）』
前回『数学勉強ノート（偏微分と全微分）』

前半は線形座標変換について重点的に解説する。まずベクトル空間の定義から導入し、点の直交座標系における成分表示が、正規直交基底によるベクトルの展開の係数に対応していることを示す。

次に斜交座標系を考えたときにも、双対ベクトル空間を考えることで直交座標系のときと同様の好ましい性質が成り立つことを示す。またテンソル解析の導入として反変と共変の概念をさわり程度に解説する。

続いて線形座標変換と、線形座標変換に際して変化しない量である不変量について説明する。不変量は座標の取り方に依存しない本質的な量と考えられるので、多様体論と密接に結びつき、物理学や幾何学において非常に重要視されるためここで解説する。

最後に非線形座標変換への導入として線形座標変換を表す行列とJacobi行列の対応を見る。またこの時点で微分を用いて反変性と共変性を定義できることから、新たにいくつかの不変量を見出すことが可能となるためこれらについて触れる。

参考

双対空間、斜交座標系、反変性や共変性、テンソル、各種の不変量について互いの関連性をまとめながら説明している書籍は私の知る限り少ない。この記事を書くときに大いに参考にさせていただいた『物理のかぎしっぽ』がもっとも丁寧な部類である。

まず『物理のかぎしっぽ』を読み、次に『テンソル解析』を読めば、この記事の前半に書いてある内容はほとんど把握できるだろう。多様体の書籍はどれもクセが強く不親切なものが多い（この記事で書かれているようなことは「知っていることが前提」で書かれている）ので選ぶときは適当でよく、むしろ何冊か読むほうがよい。また『解析力学I』は99ページまでに「数学的準備」として多様体と微分幾何の周辺の話が非常によくまとめられており、多様体の概念と物理的な概念との結びつきが簡潔明快に説明されている貴重な書物である。

『テンソル解析』（David C. Kay, Custodio De La Cruz Yancarlos Josue）
『線形代数』（佐武一郎）
『多様体の基礎』（松本幸夫）
『微分幾何』（細野）
『関数解析』（黒田成俊）
『ウェーブレット』（新井仁之）
『解析力学I』（山本義隆、中村孔一）
『物理のかぎしっぽ』
『EMANの物理学』
『痛恨の一撃。』
東京電気大講義資料
神戸大学講義資料
東京大学講義資料
香川高等専門学校講義資料
QuantEcon "Orthogonal Projections and Their Applications"
USC Research Computing Facility "Wedge Products and the Determinant"

点の表現と座標系

科学においては点や物体がどこにあってどんな運動をしているのかはとても重要な情報です。

物体の位置と運動を精確に記述するために人類が発明した道具が「座標系」です。私たちが「座標系」と呼ぶもので一番古いのは1637年のデカルトによる『方法序説』における「直交座標系（デカルト座標系）」です。座標系とは要するに「地図の緯線と経線」の概念の一般化ですが、緯線と経線は紀元前3世紀のエラトステネスの世界地図で既に使われていることを考えると、「空間を区切って位置を数字の組で表現する」という考えがいかに古い起源を持っているかが伺われます¹。

地図を描く上で重要になるのは

何を基準として
- 北はどちらなのか
- 縮尺はどれくらいか
原点はどこで
- 地図の真ん中はどこにあるのか
対象がどこに見えるか
- どちらにどれくらい進んだ場所にあるか

であり、これらの情報を数学的に表現する方法のひとつが「座標系」です。

座標系と座標変換

簡単なところから始めます。私たちは普通なにかの点を見たとき、それが存在することはわかっても、その位置を表す方法を知りません。とりあえず存在することはわかるので$p$と名前をつけましょう。

この点$p$の位置を知るため、適当なところに原点(origin)$O$を取ります。

そして基準となる座標軸(coordinate axis)を導入することでようやく点$p$の位置を知ることができます。

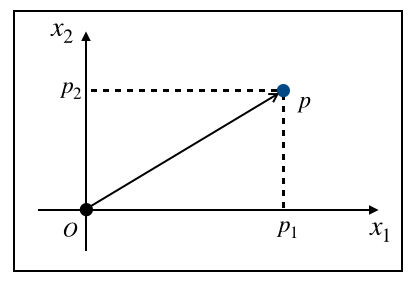
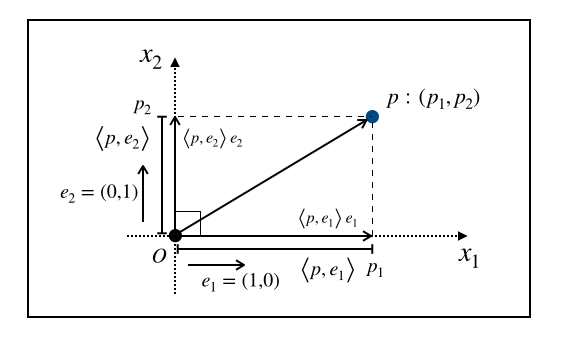
つまり私たちは原点$O$と座標軸$X=\{x_1, x_2\}$を定めることで、はじめて$p \, \colon (p_1, p_2)$のように点を数の組で表現できるようになります。このように基準となる点$O$と、方向と長さの指標$X$を定めることを「座標系(coordinate system)を定める」と言います。

座標系は人間が勝手に好きなように定めるものです。つまりこれと同じ点$P$を別の人が見たら、まったく異なった座標軸を考えるかもしれません。たとえばあなたのすぐ右隣にいる人にとっては次のように座標軸を取るほうが都合がいいかもしれないからです。

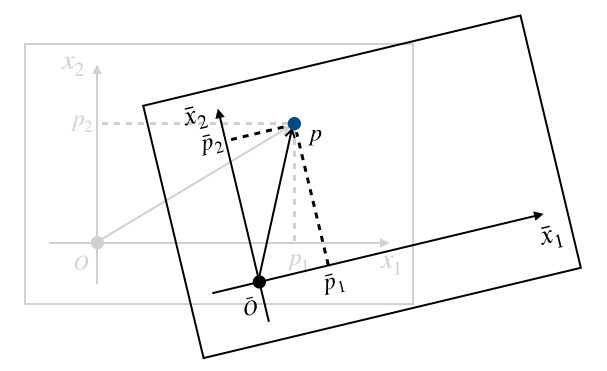
「あくまで座標軸$X$における点$p$の表現だ」ということを明記したいときは$p=(p_1, p_2)_X$のように表記することにします²。座標軸$X$とは別の座標軸$\overline{X} = \{\overline{x}_1, \overline{x}_2\}$による点$p$の表現を$p \, \colon (\overline{p} _ 1, \overline{p} _ 2)$や、$p=(\overline{p} _ 1, \overline{p} _ 2) _ {\overline{X}}$のように表記します。

ここで$p \, \colon (p_1, p_2)$と$p= (p_1, p_2)_X$で$\,\colon\,$と$=$を使い分けているのには一応理由があります。点$p$は「座標軸を取る前から存在する何か」ですから、座標系$X, \overline{X}$でそれぞれ着目している点は同じものです。ここで$p=(p _ 1, p _ 2), p=(\overline{p} _ 1, \overline{p} _ 2)$と書いてしまった場合、数式的には$(p _ 1, p _ 2) = (\overline{p} _ 1, \overline{p} _ 2)$が成り立っているかのように見えてしまいますが、実際は$p _ 1 \neq \overline{p} _ 1, p _ 2 \neq \overline{p} _ 2$です。また逆に$p _ 1 = \overline{p} _ 1, p _ 2 = \overline{p} _ 2$だったとしても$(p _ 1, p _ 2)$と$(\overline{p} _ 1, \overline{p} _ 2)$が同じ点を指しているとは限りません³。

一方で$(p _ 1, p _ 2) _ X = (\overline{p} _ 1, \overline{p} _ 2) _ \overline{X}$は「左辺と右辺で点の表現の基準が違うのだから、素直に$p _ 1 = \overline{p} _ 1, p _ 2 = \overline{p} _ 2$が成り立つとは考えにくい」ため、さしあたり問題はありません。

$p _ 1 \neq \overline{p} _ 1, p _ 2 \neq \overline{p} _ 2$であることはわかりましたが、これらはなんらかのルールにしたがってお互いを結びつけることができるかもしれません。以下の等式
$$
\left\{
\begin{align}
\overline{p} _ 1 &= \varphi _ 1(p _ 1, p _ 2) \\
\overline{p} _ 2 &= \varphi _ 2(p _ 1, p _ 2)
\end{align}
\right.
$$の関係が成り立つとき、写像$\varphi=(\varphi_1, \varphi_2)$⁴を$X$から$\overline{X}$への座標変換(coordinate transformation)といいます。この$\varphi$の性質によって「線形座標変換」「非線形座標変換」など、座標変換もいろいろ分類されます。

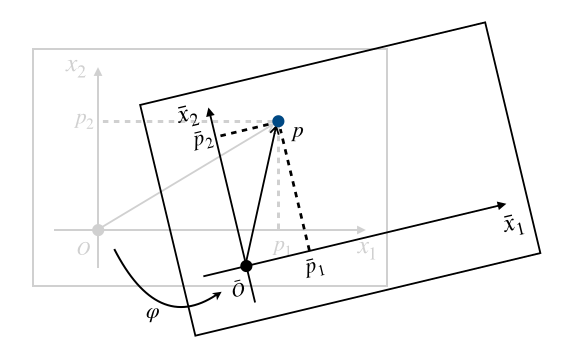
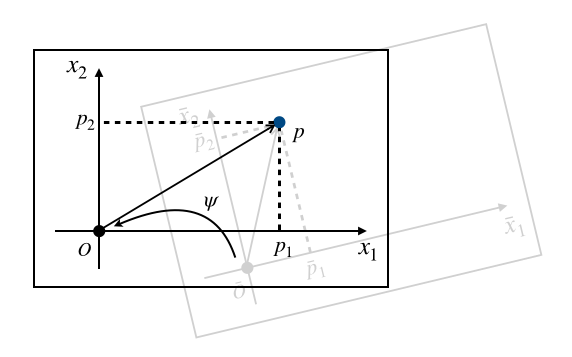
座標変換$\varphi$が全単射であるとき、新たな座標系$\overline{X}$は許容座標であるといいます。このとき$\varphi$の逆写$\psi = \varphi^{-1}$によって、逆向きの座標変換
$$
\left\{
\begin{align}
p _ 1 &= \psi _ 1(\overline{p} _ 1, \overline{p} _ 2) \\
p _ 2 &= \psi _ 2(\overline{p} _ 1, \overline{p} _ 2)
\end{align}
\right.
$$を定義することができます。

次元が大きい場合にも
$$
\left\{
\begin{align}
\overline{p} _ 1 &= \varphi _ 1(p _ 1, p _ 2, \ldots, p _ n) \\
\overline{p} _ 2 &= \varphi _ 2(p _ 1, p _ 2, \ldots, p _ n) \\
\vdots \\
\overline{p} _ m &= \varphi _ 2(p _ 1, p _ 2, \ldots, p _ n) \\
\end{align}
\right. \tag{1}
$$のように一般化することができます⁵。いちいちすべて書き下すのが面倒臭いので$(1)$式を
$$
\overline{p} = \varphi(p)
$$と書くことが多い（これはこの記事に限った話ではありません）ので、単に$p, \overline{p}$と書かれている場合は何次元での話なのか文脈から判断するクセをつけてください。

ではもっとも簡単な線形座標変換の説明に入るため、ベクトル空間の説明をしましょう。

ベクトル空間

今まで点$p$を$p=(p _ 1, p _ 2) _ X$のように数の組で表現してきましたが、これは実は点$p$を含む空間がいくつか都合のいい性質を満たさなければできない表現⁶です。数学的にはそういった都合のいい空間はベクトル空間として定式化されることが多いです。

$V$が体$\mathbb{K}$上のベクトル空間(vector space)であるとは、$V$が以下の性質を満たすことをいいます（参考）⁷。

加算について閉じる
- $\forall x, y \in V, \,\, x + y \in V$
加法の交換法則が成り立つ
- $\forall x, y \in V, \,\, x + y = y + x$
加法の結合法則が成り立つ
- $\forall x, y, z \in V, \,\, x + (y + z) = (x + y) + z$
加法の零元が存在する
- $\exists 0 \in V, \forall x \in V, \,\, x + 0 = 0 + x = x$
加法の逆元が存在する
- $\forall x \in V, \exists (-x) \in V, \,\, x + (-x) = (-x) + x = 0$
スカラー積について閉じる
- $\forall \lambda \in \mathbb{K}, \forall x \in V, \,\, \lambda x \in V$
スカラー積の結合法則が成り立つ
- $\forall \lambda, \mu \in \mathbb{K}, \forall x \in V, \,\, \lambda (\mu x)=(\lambda \mu) x$
スカラー積の零元が存在する
- $\exists 0 \in \mathbb{K}, \forall x \in V, 0 x = 0$
スカラー積の単位元が存在する
- $\exists 1 \in \mathbb{K}, \forall x \in V, 1 x = x$
スカラー積と加法の分配法則が成り立つ
- $\forall \lambda \in \mathbb{K}, \forall x, y \in V, \,\, \lambda (x + y) = \lambda x + \lambda y$

これらの性質さえ満たせばなんでもベクトルとして扱って構いません。高校で習った「数の組」以外にも様々なベクトル空間を考えることができるということです⁸。

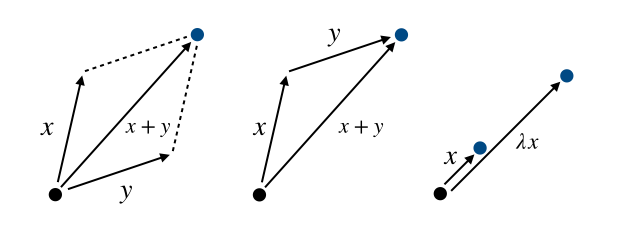
この時点で、点の足し算とスカラー倍によって別の点を表現することができるようになりました。幾何的には次の図のように表されます。$x+y$には「平行四辺形の対角線」「ベクトル$x$の終点を$y$の分だけずらす」の2通りの解釈の仕方があります。$\lambda x$は単位長さが$x$のベクトルに沿って$\lambda$分だけ進むことです。

$n$個の数の組を$\{ x _ i \} = \{ x _ i \} _ {i=1}^n = \{x _ 1, x _ 2, \ldots, x _ n \}$と表記することにします。$n$個のスカラーの組$\{a _ i\} _ {i=1} ^ n$と$n$個のベクトルの組$\{v _ i \} _ {i=1} ^ n$を
$$
\sum_{i=1}^n a _ i v _ i = a _ 1 v _ 1 + a _ 2 v _ 2 + \cdots + a _ n v _n
$$のように足し合わせることを、$\{v _ i\}$の$\{a _ i\}$による線型結合(linear combination)といいます。ある$\{v _ i\}$についての方程式
$$
a _ 1 v _ 1 + a _ 2 v _ 2 + \cdots + a _ n v _n = 0
$$を満たす$\{a _ i\}$が$\,\forall i, \, a _ i = 0\,$だけであるとき、$\{v _ i\}$は線型独立(linearly independent)であるといいます。$\{v _ i\}$が線型独立でないときは線形従属(linearly dependent)といいます。

内積

ベクトル空間$V$に次の性質を満たす演算を導入できるとき、その演算を内積(inner product)と呼びます。内積は超重要です。内積を制する者は現代科学を制すると言っても過言ではありません。

内積は実数値を取る
- $\left< x, y \right> \in \mathbb{R}$
線型性が成り立つ（$c \in \mathbb{R}$）
- $\left< x + y, z \right> = \left< x,z \right> + \left< y,z \right>$
- $\left< cx,y \right> = c \left< x,y \right>$
対称性が成り立つ
- $\left< x,y \right> = \left< y,x \right>$
正定値性を持つ
- $\left< x,x \right> \geq 0$
非退化である
- $\left< x,x \right> = 0 \Rightarrow x = 0$

たとえば$x, y \in \mathbb{R}^n$についての標準内積(standard inner product)は以下のように定義されます。これは高校でも習う内積$x \cdot y$です。
$$
\left< x, y \right> = x \cdot y = x^\mathrm{T} y = \sum_{i=1}^n x_i y_i
$$内積の定義の仕方は実は1通りではなく、いろいろな定義の仕方があります。たとえば正定値対称行列$G \in \mathbb{R}^{n \times n}$を考えて、
$$
\left< x, y \right> _ G = x^\mathrm{T} G y = \sum _ {i=1}^n \sum _ {j=1}^n g _ {ij} x _ i y _ j
$$で定義される演算は一般化内積と呼ばれ、同様に内積の性質を満たします。なぜならば正定値対称行列$G$はある直交行列$P$と対角行列$\Lambda = \mathrm{diag}\{\lambda _ 1, \lambda _ 2, \ldots, \lambda _ n\}\,\,(\forall i, \lambda _ i > 0)$を用いて
$$
G = P \Lambda P^\mathrm{T}
$$と固有値分解することができますから、
$$
\Sigma = \Lambda^{\frac{1}{2}} = \mathrm{diag}\left\{\sqrt{\lambda _ 1}, \sqrt{\lambda _ 2}, \ldots, \sqrt{\lambda _ n}\right\}
$$を用いて
$$
\begin{align}
x^\mathrm{T} G y &= x^\mathrm{T} P \Lambda P^\mathrm{T} y \\
&= x^\mathrm{T} P \Sigma \Sigma^\mathrm{T} P^\mathrm{T} y \\
&= (x^\mathrm{T} P \Sigma)(\Sigma^\mathrm{T} P^\mathrm{T} y) \\
&= \left<\Sigma^\mathrm{T} P^\mathrm{T} x, \Sigma^\mathrm{T} P^\mathrm{T} y \right> \\
&= \left< B^\mathrm{T} x, B^\mathrm{T} y \right> \quad \mathrm{where}.\, B = P \Sigma
\end{align}
$$のようにベクトル$x,y$に線形変換$B^\mathrm{T}$を施した空間での標準内積の形に落とし込めるからです。この正定値対称行列$G=g _ {ij}$を計量テンソル(metric tensor)といいます⁹。

他にも、区間$[a, b]$で定義された連続関数$f, g \in C _ 0([a,b])$についてリーマン積分によって
$$
\left< f, g \right> = \int _ a ^ b f(x)g(x) dx
$$で定義された演算$\left< \cdot , \cdot \right>$も内積の性質を満たしますので確認してみてください。関数解析の第一歩です。

$C _ 0 ([a,b])$上にリーマン積分で定義された内積は完備¹⁰ではないため、ただのベクトル空間よりも性質のいいヒルベルト空間にするためには可積分関数の集合上でルベーグ積分によって内積を定義する必要がありますが、ヒルベルト空間まで踏み込むには余白が狭すぎる。

ノルム

ノルム(norm)はベクトルの長さみたいなもので次の性質を満たすベクトル空間$V$上の演算$\| \cdot \|$として定義されます。

独立性
- $\| x \| = 0 \Rightarrow x = 0 \quad (x \in V)$
斉次性
- $\| ax \| = \left| a \right| \| x \| \quad (a \in \mathbb{R}, x \in V)$
劣加法性
- $\| x + y \| \leq \| x \| + \| y \| \quad (x, y \in V)$

ノルムと内積は別々の概念ですが、内積が定義されたベクトル空間では内積によってベクトルのノルムを定義することができます。次の式
$$
\|x \| = \sqrt{\left< x, x \right>} \in \mathbb{R}
$$で定義される演算がノルムの定義を満たすことは、内積$\left< \cdot , \cdot \right>$の定義から証明することができます。このように定義されたノルムを内積によって誘導されるノルムといいます。標準内積を用いれば
$$
\|x \| = \sqrt{\left< x, x \right>} = \sqrt{(x _ 1) ^ 2 + (x _ 2) ^ 2}
$$となりますので高校数学で見慣れた形になります。

内積と、内積から誘導されたノルムが定義された空間では、$0$でない任意の2つのベクトル$x, y \in V$に対して、ベクトルが成す角$\theta$を
$$
\cos \theta = \frac{\left< x, y \right>}{\| x \| \cdot \| y \|}
$$として定義することができます。$\cos \theta = 0$のとき、すなわち$\left< x, y \right> = 0$のとき$x, y$は直交するといいます。

ベクトルの類似度は機械学習の分野ではコサイン類似度(cosine simularity)という、データどうしの類似度を測る指標のひとつとしてしばしば使われます。話が逸れるのでこっちの記事で説明しておきましたが、コサイン類似度は単にベクトルどうしの相関係数をはかることにほぼ等価なので$\cos \theta = 1$に近いほど「強い正の相関」、$\cos \theta = -1$に近いほど「強い負の相関」を意味し、$\cos \theta = 0$ならば「無相関」です。

バナッハ空間まで踏み込むには余白が（略

直交座標系、基底と正射影（点の表現その1: ベクトルの成分表現）

いままで何気なく$p=(p _ 1, p _ 2) _ X$と書いてきましたが、実は$p, p _ 1, p _ 2, X$は内積を用いて結びつけることができます。

内積の重要な性質のひとつは、$x \neq 0, y \neq 0, x \neq y$である$x, y$についても$\left< x, y \right> = 0$を満たすものが存在するということです。たとえば$e _ 1 = (1, 0)^\mathrm{T}, e _ 2 = (0, 1)^\mathrm{T}$については
$$
\left< e _ 1, e _ 2 \right> = \left(\, 1 \,\, 0 \, \right) \left(
\begin{matrix}
0 \\
1
\end{matrix}
\right) = 1 \cdot 0 + 0 \cdot 1 = 0
$$です。

$\left< x, y \right> = 0 \,\,(x \neq 0, y \neq 0, x \neq y)$を満たす$x,y$は互いに直交する(orthogonal to each other)といいます。互いに直交するベクトルどうしの線型結合で他のベクトルを表現すると、なかなかいいことがあります。その前に基底の説明が必要ですね。

あるベクトル空間$V$に属するすべてのベクトルを互いに線型独立な有限な$n$個のベクトル$\{ e _ i \} _ {i=1} ^ n$の線型結合で表せるとき、$X = \{ e _ i \} _ {i=1} ^ n$をベクトル空間$V$の基底(basis)といいます。基底を定めることは座標軸を定めることとほぼ同じです¹¹。

基底から任意に2つ選んだ相異なるベクトルが互いに直交するとき、すなわち
$$
\left< e _ i, e _ j \right> =
\begin{cases}
\| e _ i \| ^ 2 &\quad (i = j) \\
0 &\quad (i \neq j)
\end{cases}
$$が成り立つとき、この基底は直交基底(orthogonal basis)であるといいます。特に直交基底に属する任意のベクトルのノルムが$1$であるとき、すなわち
$$
\left< e _ i, e _ j \right> =
\begin{cases}
1 &\quad (i = j) \\
0 &\quad (i \neq j)
\end{cases} \tag{2}
$$が成り立つとき、この直交基底は正規直交基底(orthonormal basis)であるといいます。$(2)$式の条件をひと目でわかるように行列で書けば
$$
X ^ \mathrm{T} X =
\left(
\begin{matrix}
e _ 1 ^ \mathrm{T} \\
e _ 2 ^ \mathrm{T} \\
\vdots \\
e _ n ^ \mathrm{T}
\end{matrix}
\right)
\left(
\begin{matrix}
e _ 1
e _ 2
\cdots
e _ n
\end{matrix}
\right)=
\left(
\begin{matrix}
e _ 1 ^ \mathrm{T} e _ 1 & e _ 1 ^ \mathrm{T} e _ 2 & \cdots & e _ 1 ^ \mathrm{T} e _ n \\
e _ 2 ^ \mathrm{T} e _ 1 & e _ 2 ^ \mathrm{T} e _ 2 & \cdots & e _ 2 ^ \mathrm{T} e _ n \\
\vdots & \vdots & \ddots & \vdots \\
e _ n ^ \mathrm{T} e _ 1 & e _ n ^ \mathrm{T} e _ 2 & \cdots & e _ n ^ \mathrm{T} e _ n
\end{matrix}
\right)=
\left(
\begin{matrix}
1 & 0 & \cdots & 0 \\
0 & 1 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & 1
\end{matrix}
\right)=
I \tag{3}
$$となります。

正規直交基底にはいろいろといい性質があるのですが、そのうちのひとつは「正射影の値と基底展開の係数が一致する」という素晴らしいものです。

ベクトル$u$のベクトル$v$への正射影（または直交射影。orthogonal projection）の値$\alpha$は以下の式
$$
\alpha = \left< u, \frac{v}{\| v \|} \right> \tag{4}
$$によって定義され、またこの$\alpha$を用いて
$$
a = \alpha \frac{v}{\| v \|} = \frac{\left< u, v \right>}{\| v \| ^ 2} v \tag{5}
$$で定義されるベクトル$a$をベクトル$u$のベクトル$v$への正射影ベクトルといいます。

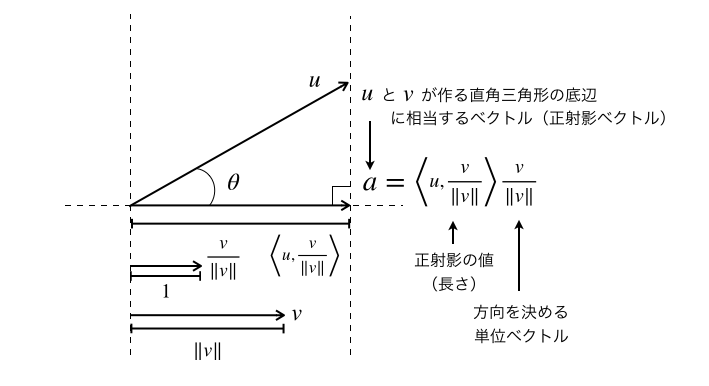
$\| v \| = 1$のとき、$(4), (5)$式はもっと見やすくなります。
$$
\begin{align}
\alpha &= \left< u, v \right> \\
a &= \alpha v = \left< u, v \right> v
\end{align}
$$そして都合のいいことに正規直交基底はすべての基底ベクトル$e _ i$について$\| e _ i \| = 1$です。

この性質を用いると、正規直交基底で展開したときの各基底ベクトルに対応する成分を簡単に求めることができます。ベクトル$x$が正規直交基底$\{ e _ i \}$によって
$$
x = x _ 1 e _ 1 + x _ 2 e _ 2 + \cdots + x _ n e _ n
$$と表せるとき、ベクトル$x$と基底ベクトル$e _ i$との内積を計算すると、内積の線型性と$(2)$式から
$$
\begin{align}
\left< x, e _ i \right> &= \left< x _ 1 e _ 1 + x _ 2 e _ 2 + \cdots + x _ n e _ n, e _ i \right> \\
&= x _ 1 \left< e _ 1, e _ i \right> + x _ 2 \left< e _ 2, e _ i \right> + \cdots + x _ i \left< e _ i, e _ i \right> + \cdots + x _ n \left< e _ n, e _ i \right> \\
&= x _ 1 \cdot 0 + x _ 2 \cdot 0 + \cdots + x _ i \cdot 1 + \cdots + x _ n \cdot 0 \\
&= x _ i
\end{align} \tag{6}
$$となり、任意のベクトルと$i$番目の基底ベクトルとの内積を取ると、その基底ベクトルに対応する展開係数が求まることがわかります。そしてこれが「正射影の値と基底展開の係数が一致する」ということです。私たちは$(6)$式の関係により、任意のベクトル$x \in V$を$V$の正規直交基底$\{ e _ i \}$を用いて
$$
x = \sum _ {i=1} ^ n \left< x, e _ i \right> e _ i = \left< x, e _ 1 \right> e _ 1 + \left< x, e _ 2 \right> e _ 2 + \cdots + \left< x, e _ n \right> e _ n
$$と基底展開することができるようになりました。

さらに言えば、この正規直交基底による展開こそが普段私たちが何気なく用いている$p \colon (p _ 1, p _ 2, \ldots, p _ n)$のようなデカルト座標での点の表現です。実際に2次元空間上の点$p$について考えてみると、正規直交基底
$$
e _ 1 = (1, 0) ^ \mathrm{T}, \quad e _ 2 = (0, 1) ^ \mathrm{T}
$$を取れば
$$
p = \left< p, e _ 1 \right> e _ 1 + \left< p, e _ 2 \right> e _ 2
$$と展開できることになり、$p _ 1 = \left< p, e _ 1 \right>, p _ 2 = \left< p , e _ 2 \right>$と置いて展開係数だけを並べた$p \colon (p _ 1, p _ 2)$がよく見るデカルト座標系での点の表現です。デカルト座標系は基底が自明なので省略した表記をしているのだと考えることもできます。

基底展開による表示は電磁気学や物性物理学などの分野でよく使われます。というのも基底展開による表示を行う限りは別に正規直交基底でなくても正確に点の位置を示せるからです。たとえば結晶学における物体の結晶格子の中でも、単斜晶系や三斜晶系では単位となる結晶構造が直方体を傾けた形をしているため、その単位結晶に沿ってあえて直交していない基底を選択したほうが応力の解析などが行いやすくなります¹²。

正規直交基底でない一般の基底による座標系は斜交座標系(oblique coordinate system)と呼ばれます。

斜交座標系と双対空間（点の表現その2: 反変成分と共変成分）

先ほどまでの議論は正規直交基底の性質に依存していたので斜交座標では一般には成り立ちませんが、実は正規直交基底でない基底を考えたときも、その双対基底と一緒に考えることでほぼ同様の基底展開が可能になります。また、後で解説する反変と共変の概念にも繋がっていくので、ここで解説しておこうと思った次第です。

では双対空間の話からしておきましょう。ベクトル空間$V$から実数$\mathbb{R}$への線形写像$f \colon V \to \mathbb{R}$全体の集合を$V$の双対空間(dual space)といい$V ^ \ast$と表します。たとえば$n$次元数ベクトル空間$\mathbb{R}^n$の元$x = (x _ 1, x _ 2, \ldots, x _ n) ^ \mathrm{T} \in \mathbb{R}^n$について、以下の形で定義される写像
$$
f(x) = a _ 1 x _ 1 + a _ 2 x _ 2 + \cdots + a _ n x _ n
$$は線形性を満たすので線形写像です。線形性とは$\forall x, y \in \mathbb{R}^n, \forall k \in \mathbb{R}$について
$$
\begin{align}
f(x + y) &= f(x) + f(y) \\
f(kx) &= kf(x)
\end{align}
$$が成り立つことです（簡単なので各自で証明してください）。行列の表記を用いれば
$$
f(x) = a ^ \mathrm{T} x = \left(
\begin{matrix}
a _ 1
a _ 2
\cdots
a _ n
\end{matrix}
\right) \left(
\begin{matrix}
x _ 1 \\
x _ 2 \\
\vdots \\
x _ n
\end{matrix}
\right)
$$とも書けますので、$f= a ^ \mathrm{T}$と解釈すれば、列ベクトルで表現されるベクトル空間$\mathbb{R}^n$の双対空間$(\mathbb{R}^n) ^ \ast$の元は行ベクトル$a ^ \mathrm{T} \in (\mathbb{R}^n) ^ \ast$で表すことができます。

ベクトル空間$V$の双対空間$V ^ \ast$に、和とスカラー倍の演算
$$
\begin{align}
(f + g)x &= f(x) + g(x) \\
(kf)x &= k(f(x))
\end{align}
$$を導入することで、$V ^ \ast$もまた一般にベクトル空間になります（$V ^ \ast$がベクトル空間の公理を満たすことは各自で確認してください）。このことを受けて$f \in V ^ \ast$を双対ベクトル(dual vector)といい、$V ^ \ast$を双対ベクトル空間(dual vector space)ともいいます。

ベクトル空間$V$に内積が定義されている場合、ベクトル空間$V$の元$x$に双対空間$V ^ \ast$の元$x ^ \ast$を一意に対応づける写像$v$を以下の式で定義することができます¹³。
$$
x ^ \ast = v(x) = \left< x, \cdot \right>
$$こう書かれると難しい感じがしますが、先ほども述べたように$x \in \mathbb{R}^n$ならばただ転置を取るだけで$v(x) = x ^ \mathrm{T}$です¹⁴。また今まで内積を$\left< \cdot, \cdot \right> \colon V \times V \to \mathbb{R}$として扱ってきましたが、$x ^ \mathrm{T} y$は$V ^ \ast \times V \to \mathbb{R}$のようにも見えるため、$\left< \cdot \mid \cdot \right> \colon V ^ \ast \times V \to \mathbb{R}$としての解釈も許すことにします。すなわち
$$
\left< x, y \right> = x ^ \mathrm{T} y = \left< x ^ \mathrm{T} \mid y \right>
$$であり、
$$
\left< x ^ \mathrm{T} \mid y \right> = \left< v ^ {-1}(x ^ \mathrm{T}), y \right>
$$です。これはもともと量子力学の分野でブラケット記号(bra-ket notation)として使われるものです（用法もまったく同じです）。この記事では内積の左側が$V$の元なのか$V ^ \ast$の元なのかはっきりさせるためにブラケット記法を採用することにします。

ベクトル空間$V$の基底$X = \{e _ i\} _ {i=1} ^ n \subset V$について、ベクトルの組$X ^ \ast = \{e ^ i\} _ {i=1} ^ n \subset V ^ \ast$が存在して、
$$
\left< e ^ i \mid e _ j \right> =
\begin{cases}
1 &\quad(i = j) \\
0 &\quad(i \neq j)
\end{cases} \tag{7}
$$が成り立つとき、このベクトルの組$X ^ \ast$を基底$X$の双対基底といい、$X$と$X ^ \ast$は双直交であるといいます。双対基底は双対ベクトル空間$V ^ \ast$の基底となっています（証明）。$(7)$式の条件は$(3)$式と同様に行列形式で書けば
$$
X ^ \ast X = I
$$です。$X$が正則行列ならば明らかに$X ^ \ast = X ^ {-1}$ですから、変わったことを考えなければ単に逆行列を計算するだけで双対基底を求めることができます¹⁵。この時点で一般に$e ^ i \neq e _ i ^ \mathrm{T}$である点に注意してください。

$x ^ \ast$は$V ^ \ast$の元ですから、双対基底$X ^ \ast$を用いて一意に
$$
x ^ \ast = v ^ {(1)} e ^ 1 + v ^ {(2)} e ^ 2 + \cdots + v ^ {(n)} e ^ n
$$と基底展開できます。いま右肩の添え字は$e ^ i$のように双対空間に関わるものであることを示しているため、係数については$v ^ {(i)}$として( )をつけて区別しています。$v ^ {(i)}$が具体的にどんな数になるか気になるわけですが、ここで$x ^ \ast$ともとのベクトル空間$V$の$i$番目の基底ベクトルとの内積を取ってみると、$(2)$式の性質から
$$
\begin{align}
\left< x ^ \ast \mid e _ i \right> &= \left< v ^ {(1)} e ^ 1 + v ^ {(2)} e ^ 2 + \cdots + v ^ {(n)} e ^ n \mid e _ i \right> \\
&= v ^ {(1)} \left< e ^ 1 \mid e _ i \right> + v ^ {(2)} \left< e ^ 2 \mid e _ i \right> + \cdots + v ^ {(i)} \left< e ^ i \mid e _ i \right> + \cdots + v ^ {(n)} \left< e ^ n \mid e _ i \right> \\
&= v ^ {(1)} \cdot 0 + v ^ {(2)} \cdot 0 + \cdots + v ^ {(i)} \cdot 1 + \cdots + v ^ {(n)} \cdot 0 \\
&= v ^ {(i)}
\end{align}
$$となります。したがって$\forall x ^ \ast \in V ^ \ast$について
$$
x ^ \ast = \sum _ {i=1} ^ n \left< x ^ \ast \mid e _ i \right> e ^ i
$$という基底展開が成立することになり、正規直交基底における基底展開とよく似たとてもシンプルなものになります。すなわち斜交座標の基底ベクトルによる内積の値が表しているのは、その基底ベクトルに対応する双対基底ベクトルの係数です。同様に
$$
x = w(x ^ \ast) = v ^ {-1}(x)
$$についても
$$
w ^ {(i)} = \left< e ^ i \mid x \right>
$$が成立することから、
$$
x = \sum _ {i=1} ^ n \left< e ^ i \mid x \right> e _ i
$$と基底展開できます。斜交座標の双対基底ベクトルによる内積の値が表しているのは、その双対基底ベクトルに対応するもとの基底ベクトルの係数です。

この事実を受けて、斜交座標では点$p$を$p = (b ^ {(1)}, b ^ {(2)}, \ldots, b ^ {(n)}) _ X ^ \mathrm{T}$と表現するときは
$$
b ^ {(i)} = \left< e ^ i \mid p \right>
$$であるとし、$p ^ \ast = (c ^ {(1)}, c ^ {(2)}, \ldots, c ^ {(n)}) _ {X ^ \ast}$と表現するときは
$$
c ^ {(i)} = \left< p ^ \ast \mid e _ i \right>
$$であるとします。

あとでまた触れることになりますが、もとのベクトル空間の基底を共変基底(covariant basis)、双対ベクトル空間の基底を反変基底(contravariant basis)ともいいます。共変基底との内積で表される成分$a _ i = b ^ {(i)}$をベクトルの共変成分と呼び、また反変基底との内積で表される成分$a ^ i = c ^ {(i)}$を反変成分といいます。

反変と共変はどっちがどっちか忘れがちですが、
$$
\begin{align}
a ^ i &= \left< e ^ i \mid p \right> \\
a _ i &= \left< p ^ \ast \mid e _ i \right>
\end{align}
$$なので「双対（反変）が内積の左側」「内積をとった基底の添え字がそのまま残る」と覚えておけば大丈夫です。

いま一度確認しておきますが、反変成分は共変基底と、共変成分は反変基底と合わせることでベクトルを展開できますから、それぞれ
$$
\begin{align}
p &= a ^ 1 e _ 1 + a ^ 2 e _ 2 + \cdots + a ^ n e _ n = \sum _ {i=1} ^ n a ^ i e _ i \\
p ^ \ast &= a _ 1 e ^ 1 + a _ 2 e ^ 2 + \cdots + a _ n e ^ n = \sum _ {i=1} ^ n a _ i e ^ i
\end{align}
$$と展開できます。鍵と鍵穴のように互い違いに組み合わせるのがミソです。念のため、一般には
$$
\begin{align}
\sum _ {i=1} ^ n a ^ i e _ i &\neq \sum _ {i=1} ^ n a _ i e _ i \\
\sum _ {i=1} ^ n a _ i e ^ i &\neq \sum _ {i=1} ^ n a ^ i e ^ i \\
\sum _ {i=1} ^ n a _ i e _ i &\neq \sum _ {i=1} ^ n a ^ i e ^ i
\end{align}
$$ですからね。この関係式が納得いかなければもう一度このセクションを最初から読み直したほうがいいかもしれません。

$a = (a ^ 1, a ^ 2, \ldots, a ^ n) ^ \mathrm{T}$のように反変成分だけを並べたベクトルを反変ベクトル(contravariant vector)といい、$a ^ \ast = (a _ 1, a _ 2, \ldots, a _ n)$のように共変成分だけを並べたベクトルを共変ベクトル(covariant vector)といいます。反変ベクトルを単にベクトル(vector)、共変ベクトルをコベクトル(covector)ということもあります¹⁶。

最後にもう一度整理します。もとのベクトル空間$V$の元$x$は共変基底（$\leftarrow$こいつが基準）で展開しますから、その座標成分は反変成分だと都合がよく、反変ベクトルで表現することが多いです。逆に双対ベクトル空間の元$x ^ \ast$は反変基底で展開しますから、その座標成分は共変成分だと都合がよく、共変ベクトルで表現することが多いです。

一般には$e ^ i \neq e _ i ^ \mathrm{T}$ですが、正規直交基底に限れば$X$は直交行列となるので$X ^ {-1} = X ^ T$の関係が成立し、$e ^ i = e _ i ^ \mathrm{T}$となります。正規直交基底はその双対基底が自分自身の転置になっていたので、双対空間を考えずとも基底展開できるというよい性質があったのですね¹⁷。

線形座標変換

さていよいよ線形座標変換に入りますが、線形座標変換において重要なことはここまでですべて解説が終わっているので解説することはほぼありません。

そろそろ冒頭までスクロールするのは面倒でしょうから座標変換の一般式をもう一度書いておくと
$$
\left\{
\begin{align}
\overline{p} _ 1 &= \varphi _ 1(p _ 1, p _ 2, \ldots, p _ n) \\
\overline{p} _ 2 &= \varphi _ 2(p _ 1, p _ 2, \ldots, p _ n) \\
\vdots \\
\overline{p} _ m &= \varphi _ 2(p _ 1, p _ 2, \ldots, p _ n) \\
\end{align}
\right.
$$です。線形座標変換が許容座標変換となるには$m = n$が必要条件ですから以降は$m=n$とします（必要十分条件は線形座標変換を表す行列が正則になることです）。毎回すべての成分を書くのは長ったらしいので普通は変換後の第$i$成分を代表して
$$
\overline{p} _ i = \varphi _ i(p _ 1, p _ 2, \ldots, p _ n)
$$のように略記します。逆変換は
$$
p _ i = \varphi _ i ^ {-1}(\overline{p} _ 1, \overline{p} _ 2, \ldots, \overline{p} _ n)
$$です。多様体論では上式のように「関数$\varphi$による変換であること」を明示する記法が好まれるのですが、物理学では順変換を
$$
\overline{x} _ i = \overline{x} _ i(x _ 1, x _ 2, \ldots, x _ n)
$$で表し、逆変換を
$$
x _ i = x _ i (\overline{x} _ 1, \overline{x} _ 2, \ldots, \overline{x} _ n)
$$のように表して「あくまで座標であること」を強調する記法が好まれます。この記事では状況によってわかりやすいほう（独断）を使います。

また、上式に登場する$p$と$x$で何か違いがあるのかと思うかもしれませんが、この記事内では区別しなくても問題ありません¹⁸。いままで「$p$といえば『点』っぽい」「$x$といえば『座標』っぽい」というニュアンスで使い分けていただけです。今後は$x$に統一します。

そして反変と共変についても説明したので、添え字が上につくか下につくかで意味が変わること、もとのベクトル空間の座標を表すときは反変ベクトルを利用することが多いことも説明しました。

以上の理由を踏まえて、この記事では
$$
\begin{align}
\overline{x} ^ i = \varphi ^ i(x ^ 1, x ^ 2, \ldots, x ^ n) \\
\overline{x} ^ i = \overline{x} ^ i(x ^ 1, x ^ 2, \ldots, x ^ n)
\end{align}
$$という記法を併用します。この記法は解析力学で使われる書き方です。

以下の式によって定義される座標変換
$$
\overline{x} ^ i = \varphi ^ i(x ^ 1, x ^ 2, \ldots, x ^ n) = a ^ i _ 1 x ^ 1 + a ^ i _ 2 x ^ 2 + \cdots + a ^ i _ n x ^ n = \sum _ {j=1} ^ n a ^ i _ j x ^ j \tag{8}
$$を線形座標変換といいます。$a ^ i _ j$は上付き添え字と下付き添え字をそれぞれひとつずつ持っているので、1階の反変成分と1階の共変成分を持つ2階の混合テンソルといいます。いちいち$\Sigma$を書くのが面倒くさいので$(8)$式を
$$
\overline{x} ^ i = a ^ i _ j x ^ j
$$と省略すること、すなわち「同じ文字が出てきたら$\Sigma$をとれ」という~~サボり~~約束を~~カッコつけて~~アインシュタインの規約といいます。線形座標変換を一切の省略なしに頑張って行列で書くと
$$
\left(
\begin{matrix}
\overline{x} ^ 1 \\
\overline{x} ^ 2 \\
\vdots \\
\overline{x} ^ n \\
\end{matrix}
\right) =
\left(
\begin{matrix}
a ^ 1 _ 1 & a ^ 1 _ 2 & \cdots & a ^ 1 _ n \\
a ^ 2 _ 1 & a ^ 2 _ 2 & \cdots & a ^ 2 _ n \\
\vdots & \vdots & \ddots & \vdots \\
a ^ n _ 1 & a ^ n _ 2 & \cdots & a ^ n _ n \\
\end{matrix}
\right)
\left(
\begin{matrix}
x ^ 1 \\
x ^ 2 \\
\vdots \\
x ^ n \\
\end{matrix}
\right)
$$であり、$A = (a ^ i _ j)$とすれば
$$
\overline{x} = A x \tag{9}
$$です。

$A$が正則ならばこの線形座標変換には逆変換が存在し、ある行列$B = (b ^ i _ j)$を用いて
$$
x ^ i = b ^ i _ j \overline{x} ^ j
$$と表せます。$(9)$式の両辺に左から$B$をかければ
$$
\begin{align}
B \overline{x} &= B A x \\
\Rightarrow \,\, x &= BA x
\end{align}
$$から$BA = I$が成り立ち、$B = A ^ {-1}$が導かれます。

不変量

座標変換で変化するのはあくまでも「位置の表現方法」であって、変換の前後でベクトル$v$の位置そのものが変化するわけではありません。たとえばいまあなたが回れ右をしたからといって地球が半回転して北極が移動するわけではありません。しかし$v$の位置を成分表示した反変ベクトル$x$と、変換後の反変ベクトル$\overline{x}$は一般に$x \neq \overline{x}$であり、変化しています。これは一見すれば矛盾です。

ここで思い出していただきたいのは、成分表示は基底ありきだということです。つまり$v = (x ^ 1, x ^ 2, \ldots, x ^ n) ^ \mathrm{T}$というのは共変基底$X$を省略した表現であり、再び明示すれば$v = (x ^ 1, x ^ 2, \ldots, x ^ n) _ X ^ \mathrm{T}$です。座標変換に際しては共変基底$X$も$X \to \overline{X}$という変換を受けます（だからこそ "座標" 変換なのです）し、またこれが反変ベクトルの変化をちょうど打ち消すものであれば$v$自体は変換の前後で不変であることになります。すなわち$v = (x ^ 1, x ^ 2, \ldots, x ^ n) _ X ^ \mathrm{T} = (\overline{x} ^ 1, \overline{x} ^ 2, \ldots, \overline{x} ^ n) _ \overline{X} ^ \mathrm{T}$が成り立ち、座標変換とは単に表現方法の相違に過ぎないと主張できることになります。

さて残った問題は「反変ベクトルの変化をちょうど打ち消す共変基底の変化は常に存在するか」という点ですが、これは許容座標変換については「（反変ベクトルに対しての）線形座標変換$A ^ {-1}$に際しては、（共変）基底は$A$の変換を受ける」と定義することで実現できます。

いま言葉の整合性をとるために、線形座標変換$F$について、共変基底の変換を表す行列を$A$と定義しなおします。共変基底を言葉の選び方の基準にとったということです。反変とか共変が頭の中でこんがらかってしまったときはいつも共変基底を基準に持ってくるとよいです。

これによって線形座標変換を表す式は
$$
\begin{align}
\overline{x} &= A ^ {-1} x \\
\overline{X} &= XA
\end{align}
$$と書き直されますが、実はこの表現こそが、すなわち反変ベクトルは線形座標変換$F$に際して$A ^ {-1}$という「（共変基底とは）反対の変化」を受けることこそが「反変」という名前の由来になっています。それと対比する形で「（共変基底と）共通の変化」を受けることが「共変」です。

不変性とは$A$による変化を$A ^ {-1}$で打ち消したことによる当たり前の結果なのですが、一応確認しておきましょう。$v = x ^ 1 e _ 1 + x ^ 2 e _ 2 + \cdots + x ^ n e _ n$を行列表現すると
$$
v = X x
$$となります。ただし
$$
x =
\left(
\begin{matrix}
x ^ 1 \\
x ^ 2 \\
\vdots \\
x ^ n \\
\end{matrix}
\right), \quad X =
\left(
\begin{matrix}
e ^ 1 _ 1 & e ^ 1 _ 2 & \cdots & e ^ 1 _ n \\
e ^ 2 _ 1 & e ^ 2 _ 2 & \cdots & e ^ 2 _ n \\
\vdots & \vdots & \ddots & \vdots \\
e ^ n _ 1 & e ^ n _ 2 & \cdots & e ^ n _ n \\
\end{matrix}
\right)
$$です。$e ^ j _ i$は「$i$番目の共変基底ベクトルを反変成分で表示したときの$j$番目の成分」を表します。したがって線形座標変換後のベクトル$v'$は
$$
v' = \overline{X} \overline{x} = (X A)(A ^ {-1} x) = X (A A ^ {-1}) x = X x = v
$$となりますので
$$
v' = v
$$が確認できます。

この事実はとても重要で「ベクトルを反変成分と共変基底の組み合わせで表示した場合、ベクトル自体は線形座標変換の前後で不変である」ことを意味します¹⁹。座標変換の前後で不変な対象を不変量(invariant)といいます²⁰。

特に物理学の分野ではたかだか座標変換をかけたくらいで物理法則が変わってしまっては困りますから、座標変換に関して不変な物理量としてのベクトル量²¹は反変成分と共変基底の組み合わせで表現すると都合がよいのです（物理法則自体は共変基底と同様の変化を受けるものとして扱われます）。

また、この事実の応用として「反変ベクトルと共変ベクトルの内積は不変量」という事実も導くことができます。

共変基底$X$に対して反変基底$X ^ \ast$は$X ^ \ast = X ^ {-1}$で表せる。
共変基底$X$の$A$による変換後の共変基底$\overline{X}$は$\overline{X} = XA$で表せる。

という2つの性質から、変換後の反変基底$\left( \overline{X} \right) ^ \ast$は
$$
\left( \overline{X} \right) ^ \ast = (XA) ^ \ast = (XA) ^ {-1} = A ^ {-1} X ^ {-1} = A ^ {-1} X ^ \ast
$$として導出されます。つまり線形座標変換$F$による反変基底の変換は左から$A ^ {-1}$をかけることで表現されます。共変ベクトルはこの反変基底の変化を打ち消さねばなりませんから、右から$A$がかかります。

このことを踏まえて$a, b \in V$について内積をとるとき、一度$a$を対応する双対ベクトル$v(a) = a ^ \ast \in V ^ \ast$に変換した上で共変ベクトル$(x _ i)$で表現²²し、また$b$はそのまま反変ベクトル$(y ^ i)$で表現することにします。線形座標変換$F$を$x,y$に同時に適用すると変換後は$\left( \overline{x} \right) ^ \ast = x ^ \ast A, \overline{y} = A ^ {-1} y$と表せますから、共変ベクトルが行ベクトルで反変ベクトルが列ベクトルであるというアナロジーを考慮しながら変換後に内積をとると
$$
\left< \left( \overline{x} \right) ^ \ast \mid \overline{y} \right> = \left< x ^ \ast A \mid A ^ {-1} y \right> = x ^ \ast A A ^ {-1} y = x ^ \ast (A A ^ {-1}) y = x ^ \ast y = \left< x ^ \ast \mid y \right> \tag{10}
$$となるため、変換の前後で内積の値が保存していることがわかります。

線形座標変換とJacobi行列

線形変換の重要な性質のひとつは「どこで微分しても微分の値が一定」というものです。直線を表す方程式$y = ax$はどの点で微分しても$\frac{dy}{dx} = a$であり定数です。$y=ax$は線形座標変換のもっとも簡単なケースであり、$\overline{x} = A x$はその多次元への拡張になっています。偏微分等についてわからなければ前回の『数学勉強ノート（偏微分と全微分）』をご覧ください。

試しに$(5)$式で適当な点$x = p$を選んで$x _ j$で偏微分すると
$$
\frac{\partial \overline{x} ^ i}{\partial x ^ j}(p) = a _ j ^ i
$$となります。したがって
$$
A =
\left(
\begin{matrix}
a ^ 1 _ 1 & a ^ 1 _ 2 & \cdots & a ^ 1 _ n \\
a ^ 2 _ 1 & a ^ 2 _ 2 & \cdots & a ^ 2 _ n \\
\vdots & \vdots & \ddots & \vdots \\
a ^ n _ 1 & a ^ n _ 2 & \cdots & a ^ n _ n \\
\end{matrix}
\right) =
\left(
\begin{matrix}
\frac{\partial \overline{x} ^ 1}{\partial x ^ 1} & \frac{\partial \overline{x} ^ 1}{\partial x ^ 2} & \cdots & \frac{\partial \overline{x} ^ 1}{\partial x ^ n} \\
\frac{\partial \overline{x} ^ 2}{\partial x ^ 1} & \frac{\partial \overline{x} ^ 2}{\partial x ^ 2} & \cdots & \frac{\partial \overline{x} ^ 2}{\partial x ^ n} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial \overline{x} ^ n}{\partial x ^ 1} & \frac{\partial \overline{x} ^ n}{\partial x ^ 2} & \cdots & \frac{\partial \overline{x} ^ n}{\partial x ^ n} \\
\end{matrix}
\right) = J _ A
$$が成り立ち、線形座標変換$A$のJacobi行列は行列$A$自身であることがわかりました。

逆変換$B = A ^ {-1}$についてもまったく同じ議論が成り立ち、
$$
\frac{\partial x ^ i}{\partial \overline{x} ^ j} = b _ j ^ i
$$ですが、一般に
$$
\frac{\partial \overline{x} ^ i}{\partial x ^ j} \neq \frac{1}{\frac{\partial x ^ i}{\partial \overline{x} ^ j}}
$$であることに注意してください。この等号が成立するのは$1$次元の場合だけです。

そしてこのJacobi行列が線形座標変換と非線形座標変換を繋ぐ架け橋です。微分可能な写像によって定義される非線形座標変換であれば、着目している点$p$とその周辺のごく狭い範囲では線形座標変換で近似することができ、その線形座標変換を表す行列がJacobi行列なのです。

微分を用いた議論により反変や共変といった概念は非線形座標変換にも拡張され、位置ベクトルだけでなく、より広い概念にも反変や共変、不変量といった性質を定義することが可能になります。非線形座標変換に際しても影響を受けない量が定義できるならば、計算しやすいように勝手に座標変換しても数学的に問題ないことが保証されるので、私たちは座標系をかなり自由に選択できるようになります。

反変性と共変性

いままで位置ベクトルのみを扱ってきましたが、空間の性質を考えるときに扱う対象は位置だけでは不十分で、たとえば速度ベクトル、加速度ベクトル²³、曲面の勾配、曲面の接ベクトルといった様々な対象を考察することになります。こういった対象の性質を調べるときに反変や共変の概念は重要な手がかりになるので、反変ベクトルや共変ベクトルの考え方を一般化して

共変(covariance): 対象が座標変換に際して共変基底と共通の変化を受けるとき共変性(covariance)を持つ、または共変であるという。
反変(contravariance): 対象が座標変換に際して共変基底と反対の変化を受けるとき反変性(contravariance)を持つ、または反変であるという。

と定義します。$A ^ {-1} = (\frac{\partial \overline{x} ^ i}{\partial x ^ j}), A = (\frac{\partial x ^ i}{\partial \overline{x} ^ j})$であったことを思い出せば、反変性とは$(T ^ r) _ {r = 1} ^ n$で表現される対象が座標変換に際して
$$
\overline{T} ^ i = \frac{\partial \overline{x} ^ i}{\partial x ^ r} T ^ r
$$という変換を受けることであり、共変性とは$(T _ r) _ {r = 1} ^ n$で表現される対象が座標変換に際して
$$
\overline{T} _ i = \frac{\partial x ^ i}{\partial \overline{x} ^ r} T _ r
$$という変換を受けることであると言いなおすことができます。くどいようですが、どちらの式もアインシュタインの規約で$\Sigma$が取られていることに注意してください。

たとえばもっとも基本的かつ重要な性質として、全微分は反変です。なぜならば$\overline{x} ^ i$を$x$の関数と見て全微分すると
$$
d \overline{x} ^ i = \frac{\partial \overline{x} ^ i}{\partial x ^ j} d x ^ j
$$が求まり、これは反変の定義式そのものだからです。イメージが掴みやすいように復習しておくと、全微分の式は
$$
d \overline{x} ^ i = A ^ i _ j \Delta x ^ j = \frac{\partial \overline{x} ^ i}{\partial x ^ j} \Delta x ^ j
$$の意味です。すなわち座標系$X$で基底ベクトル$x ^ j$の方向に$\Delta x ^ j$の分だけ変化させると、その変化は座標系$\overline{X}$では基底ベクトル$\overline{x} ^ i$の方向に$A ^ i _ j$倍されて反映されます。$d \overline{x} ^ i$は$\forall x ^ j$から影響を受けるので、$x ^ j$に関して総和を取ったのが上式です。

次に関数$f \colon V \to \mathbb{R}$の勾配ベクトルについて考えてみます。関数$f$はベクトル空間の点上で定義されているので変換の前後で不変です。より具体的に言うと、関数$f$の値は点$p \in V$に対応して定義されているので点$p$の表示の仕方の違いは$f$の値に影響を与えません。つまり$y = f\left(\overline{x}\right) = f(x)$です。ここで
$$
\overline{x} ^ i = \overline{x} ^ i (x ^ 1, x ^ 2, \ldots, x ^ n)
$$の記法を略記した
$$
\overline{x} = \overline{x}(x)
$$を用いると$y = f\left(\overline{x}(x)\right) = f(x)$という表記になります。勾配を計算するには点$x$を空間上で少しずらしてみなければなりませんが、このとき点$\overline{x}$は自由に動かしてよいわけではなく、点$x$の動きを点$\overline{x}$での動きに翻訳したものになります。そういった束縛の関係を$\overline{x}(x)$という書き方で表現しているわけです。

さて『数学勉強ノート（偏微分と全微分）』にしたがって$y$の全微分を計算すると
$$
dy = df = \frac{\partial f}{\partial x ^ j} d x ^ j = \frac{\partial f}{\partial \overline{x} ^ i} d \overline{x} ^ i \tag{11}
$$です。アインシュタインの規約に注意です。ここで上式の$d x ^ j$を$x ^ j$の$\overline{x}$に関する全微分とみなせば
$$
d x ^ j = \frac{\partial x ^ j}{\partial \overline{x} ^ i} d \overline{x} ^ i
$$となるので、これを$(11)$式に代入すれば
$$
df = \frac{\partial f}{\partial x ^ j}\frac{\partial x ^ j}{\partial \overline{x} ^ i} d \overline{x} ^ i
$$です。これを再び$(11)$式と比較すれば
$$
\frac{\partial f}{\partial \overline{x} ^ i} = \frac{\partial x ^ j}{\partial \overline{x} ^ i}\frac{\partial f}{\partial x ^ j}
$$が求まります（何気なく導出しましたがこれは『数学勉強ノート（偏微分と全微分）』でも解説した微分の連鎖律です）。この式は共変の定義式を満たしますので、勾配ベクトル$\nabla f = \left(\frac{\partial f}{\partial x ^ i}\right)$は共変です。

全微分は反変でした。そして$\left( \frac{\partial \overline{x} ^ i}{\partial x ^ j} \right)$は$\overline{x} ^ i \colon V \to \mathbb{R}$の勾配とみなせるので、こちらは共変です。反変と共変の内積は不変量ですから、実は面白いことに全微分は反変でありながら不変量になっています（『数学勉強ノート（偏微分と全微分）』で「この記事で意図している内容を超えてしまうので詳しくは説明しませんが」と言った部分の詳しい説明です）。

より正確には、すぐ後述するように$\{d x ^ j \} _ {j = 1} ^ n$が反変基底であり、その成分である個々の$d x ^ j$は単なる空間上の線分の長さと解釈できるので不変量になっています。これは座標系に依存しない微分の概念を定義したということであり大変興味深い事実です²⁴。

ここまで全微分や勾配に対しては単に「反変」や「共変」とだけ言ってベクトルなのか基底なのかぼかしてきましたが、全微分に関しては反変ベクトルとも反変基底とも解釈できます。$d x ^ j$は「$x ^ j$の方向に動かした」という情報を持っているのでベクトルとみなすことができ、
$$
d \overline{x} ^ i = \frac{\partial \overline{x} ^ i}{\partial x ^ j} d x ^ j
$$と書いたときに勾配のほうは係数ですから、全微分が反変基底で勾配が共変成分と解釈できるわけです。その一方で$x ^ j$の方向に動かした値にだけ着目して反変ベクトル$(dx ^ 1, dx ^ 2, \ldots, dx ^ n) ^ \mathrm{T}$として成分表示すれば上式は「反変ベクトルと共変ベクトルで内積をとったら不変量になった」とも解釈することができます。

速度ベクトルについても見ておきましょう。結論からいえば速度ベクトルは反変ベクトルですので、以下の説明では最初から上付き添え字で表現します（あとから書き直すのが面倒なので）。速度ベクトルは位置の時間微分ですから、成分は、アインシュタインの規約に注意（何度でも言います）しながら、
$$
\begin{align}
\frac{d \overline{x} ^ i}{dt} &= \frac{d \overline{x} ^ i (t)}{dt} \\
&=\frac{\overline{x} ^ i (t + \Delta t)-\overline{x} ^ i (t)}{\Delta t} \\
&=\frac{a _ j ^ i x ^ j (t + \Delta t) - a _ j ^ i x ^ j (t)}{\Delta t} \\
&= a _ j ^ i \frac{x ^ j (t + \Delta t) - x ^ j (t)}{\Delta t} \\
&= a _ j ^ i \frac{dx ^ j}{dt} \\
&= \frac{\partial \overline{x} ^ i}{\partial x ^ j} \frac{dx ^ j}{dt}
\end{align}
$$です。したがって速度ベクトルが反変ベクトルであることが示されました。

勾配ベクトルは共変ベクトルでしたから、速度ベクトルとの内積はやはり不変量です。実際に点$x(t)$における関数$f$の勾配を$\nabla f\left(x(t)\right)$とおくと、微分の連鎖律より
$$
\left< \nabla f\left(x(t)\right) \mid \frac{dx(t)}{dt} \right> = \frac{\partial f\left(x(t)\right)}{\partial x ^ i} \frac{d x ^ i (t)}{dt} = \frac{df \left( x(t) \right)}{dt} \tag{12}
$$となり、これは座標系に依存しない値を取ります。「微分の連鎖律より」は微分の説明をごまかす常套句でズルい気がするので『数学勉強ノート（偏微分と全微分）』に解説を追記しましたが、見に行くのが面倒くさい人のためにここでもう一度簡単に説明します。

まず$(12)$式の第二辺と第三辺の等号成立を確認します。$f$の$x$による全微分は
$$
df = \frac{\partial f}{\partial x ^ i} d x ^ i
$$となりますから、この両辺を$dt$で割れば
$$
\frac{df}{dt} = \frac{\partial f}{\partial x ^ i} \frac{d x ^ i}{dt}
$$です。

残るは$(12)$式の第一辺と第二辺の等号成立の確認と不変性に関する議論です。勾配ベクトル$\nabla f$は共変ベクトルですから反変基底によって以下のように展開されます（紛らわしさの回避のためここではアインシュタインの規約を使っていません）。
$$
\nabla f = \sum _ {i=1} ^ n \frac{\partial f}{\partial x ^ i} e ^ i
$$また速度ベクトルは反変ベクトルですから、共変基底で展開し、またその基底展開の係数は反変基底との内積で表せるので、
$$
\begin{align}
\frac{dx}{dt} &= \sum _ {j=1} ^ n \left< e ^ j \mid \frac{dx}{dt} \right> e _ j \\
&= \sum _ {j=1} ^ n \left< e ^ j \mid \left( \lim _ {\Delta t \to 0} \frac{x(t + \Delta t) - x(t)}{\Delta t} \right) \right> e _ j \\
&= \sum _ {j=1} ^ n \left( \lim _ {\Delta t \to 0} \frac{ \left< e ^ j \mid x(t + \Delta t) \right> - \left< e ^ j \mid x(t) \right> }{\Delta t} \right) e _ j \\
&= \sum _ {j=1} ^ n \left( \lim _ {\Delta t \to 0} \frac{ x ^ j (t + \Delta t) - x ^ j (t) }{\Delta t} \right) e _ j \\
&= \sum _ {j=1} ^ n \left( \frac{dx ^ j}{dt} \right) e _ j \quad {\rm where} \,\, \frac{dx ^ j}{dt} = \lim _ {\Delta t \to 0} \frac{ x ^ j (t + \Delta t) - x ^ j (t)}{\Delta t}
\end{align}
$$と展開できます。このように基底展開した時点で$(10)$式から不変性については明らかです。あとはこのように基底展開したときに第二辺との一致を確かめればいいだけですが、単純に内積をとってやれば$i = j$の項以外は消えることから（最後に再びアインシュタインの規約を用いて）
$$
\left< \nabla f \mid \frac{dx}{dt} \right> = \sum _ {i=1} ^ n \frac{\partial f}{\partial x ^ i} \frac{dx ^ i}{dt} = \frac{\partial f}{\partial x ^ i} \frac{dx ^ i}{dt}
$$となり第一辺と第二辺の一致が確認できました。

$(12)$式の第三辺は曲線$x(t)$（$t$を媒介変数として位置$x$が定まるから曲線とみなせる）の接線方向における$f$の微分として解釈することができ、方向微分と呼ばれています。

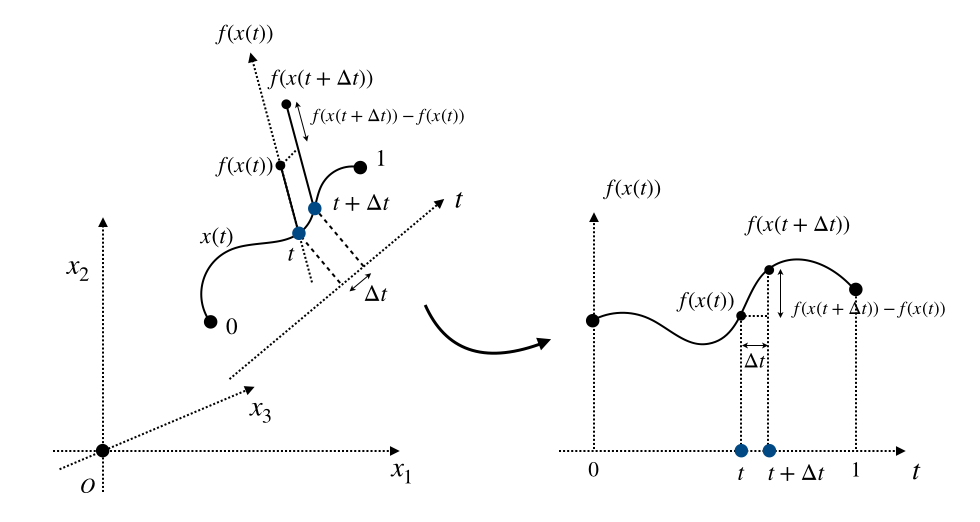
方向微分は多様体論の接ベクトルの概念へと繋がります。

（後半へ続く）

地図の原型である「写実的な絵を描く」という地球上で現代型人類のみに確認されている行動は2万年以上も前の遺跡（ラスコー洞窟）からも発見されています。紀元前7世紀ころには人類は既に「世界地図」を作ろうとしており、その後もずっと人類は世界地図を正確なもの（物理的に正確か思想宗教的に正確かはさておき）にしようと苦心してきました。現代科学との結びつきに関して言えば、16世紀にガリレイが「地動説」を唱えケプラーが「ケプラーの法則」を発見、その後17世紀になってニュートンが「万有引力」を発見しました。つまり「世界の有様を縮小した地図に描く」という発明、そして「天体の運動は地図に書ける」という発見が名も知らぬ誰かによって成され、ケプラーが天体の運動を数式によって予見し、「私たちの身の回りに存在する物体の運動を支配する方程式は天体の運動を決めるものと同じである」というニュートンの偉大な発見によって今日の「座標系をとって物体の運動を記述する」という現代科学の根幹が打ち立てられたと言えます。 ↩
点の位置を数の組で表現する場合には必ず原点の情報が必要となるので正確には$p=(p_1, p_2) _ {(O, X)}$のように書くべきかもしれませんが、座標軸自体が原点の情報を含んでいる場合が多いので$X$だけ書けば十分でしょう。 ↩
高校時代の恩師であるK藤先生が「ベクトルと違って点は$=$で書いちゃダメ」と仰っていたのはおそらくこのことでしょう。24歳になって気づくとは、実に7年越しの伏線回収。K藤先生ありがとうございます。 ↩
$\varphi$はギリシャ文字$\phi$（ファイ）の丸っこいバージョンであり、$\varphi, \phi$は座標変換を表す写像の記号としてよく使われます。$\psi$（プサイ）もよく使います。 ↩
許容座標だからといって$m=n$とは限りません。たとえば$\varphi$の定義域が半径$1$の円周上であった場合、直交座標系では$x,y$の2変数が必要ですが、極座標系では偏角$\theta$の情報があれば十分で、$m=1, n=2$でも$\varphi$を全単射にすることができます。定義域重要。 ↩
難しい言葉でいえば「有限次元ヒルベルト空間のフーリエ展開の係数を並べたもの」です。 ↩
$\forall$や$\exists$は「量化子(quantifier)」と呼ばれ、「$\forall x$」は「任意の$x$について」、「$\exists x$」は「ある$x$が（少なくともひとつ）存在して」を表します。「$\forall x, \exists y$」は「任意の$x$に対してある$y$が存在して」、「$\exists x, \forall y$」は「ある$x$に対して任意の$y$について」の意味になります。$\exists ! x$で「ただひとつの$x$が存在して」を表したりもします。慣れていない人もいると思いますので念のため。 ↩
$n$次元数ベクトル空間以外のベクトル空間については『関数解析』(黒田)などを参照してください。 ↩
実は、単に計量テンソルと言ったとき、一般にはそれが正定値であるとは限りません。ただし正定値でない計量テンソルを用いると記事中で「一般化内積」と呼んでいる式は正定値性や非退化性を満たさなくなり、通常の意味では内積とは呼べなくなります。「一般化内積」が正定値性と非退化性を満たすには、計量テンソルが正定値であることが必要十分条件です。たとえば相対性理論で扱うミンコフスキー空間のミンコフスキー計量は正定値ではなく、ミンコフスキー内積は正定値性を満たしません（ミンコフスキー内積が$0$でもベクトルが互いに直交しているとは限らない、みたいなことが起こります）。 ↩
簡単に言えば極限の収束先がもとの空間からはみ出ないことです。 ↩
基底$X$に用いるベクトルを具体的な数ベクトルなどで表現すれば原点の情報は暗黙的に基底に含まれますが、数ベクトルなどで表現する前の抽象的な点やベクトルの存在を考えてそれを基底に用いる場合はどの点を原点$O$にするかという情報を補う必要があるため$(O, X)$によって座標系を定義しなければいけません。アフィン座標系などがそうです。 ↩
多分。やったことないので知りませんしあまり適当なこと言えませんが、劈開が基底ベクトルの張る平面に沿って生じたりするはずなので、せん断応力の計算とか正規直交系でやるより楽な気がします。 ↩
@Lbfuvabさんに定義を教えていただきました。ありがとうございます。 ↩
これは関数解析におけるリースの表現定理の一部であり、$f(x)=\left< x , y _ f \right>$となる$y _ f \in \mathcal{H}$の存在と一意性はヒルベルト空間の完備性を必要とせず証明できます。 ↩
基底よりも条件を緩めたフレーム(frame,「枠」と訳す人もいる)から議論しようとすると$n$次元のベクトルに対して$m > n$なる$m$個のベクトルを用いて展開しようとするため、議論がもう少し複雑になります。フレームはウェーブレットフレームの理論などで登場します。 ↩
'covariant' の 'co-' はラテン語の接頭辞で「共に」の意味（たとえば 'coauthor' は「共著者」）を持ち 'variant' は変数(variable)と同語源なので「共に変化する変数」の意味です。一方でコベクトルの 'co-' も同語源ですが、こちらは圏論(category theory)で「双対の」を意味する接頭辞として導入されたもので「余」と訳します（たとえば「正弦」を意味する 'sine' に対して 'cosine' は「余弦」）。コベクトルも日本語では「余ベクトル」ともいいます。 ↩
たとえばフーリエ展開は正規直交基底を用いた手法なので双対基底を登場させなくても議論できますが、ウェーブレット展開のように基底を複雑にすると正規直交基底ではなくなることがあり、その場合は逆変換が成り立つために双対基底が重要になります。 ↩
物理学において「点」といえば2種類の意味があります。ひとつは質点のように「空間のどこかにある物理的な対象（物体）」であって、その座標成分は「点が空間上で占める位置の情報」であり、点が持つ性質のひとつにすぎません。たとえば質点は座標成分の他に質量や速度の情報を持っています。もうひとつは「物体どうしが作用する場としての空間上での位置」を表す点であり「空間上の2つ以上の位置を区別するための情報」です。古典力学の世界では空間の点それ自体は位置情報以外の情報は持たず、物体としての点とは区別されています。たとえば「力が作用したことによる物体の移動（真の力による移動：物体のほうが動いた）」と「座標変換による物体の位置情報の変化（慣性力による移動：空間の点のほうが動いた）」は別物です。本記事で扱っているのは「ある空間の点と別の空間の点の対応関係」なので、空間の点を表す変数としてのニュアンスが強い$x$を用います。また仮に物質の点と考えたとしても空間のある点に固定されていて空間の点といっしょに動くので、今回は区別する必要はありません。 ↩
双対ベクトル$v ^ \ast$を共変成分と反変基底で表現した場合も線形座標変換の前後でベクトル自体を不変にすることができます。もとの空間で成り立つ命題は双対空間で成り立つ命題に翻訳できるという重要な事実は「双対定理」として一般化されています。 ↩
不変量は座標変換に依存しないので「物体や空間の形状が持つ本質的な何か」であるという意味で「幾何的な対象」と呼ばれることもあります。 ↩
言うまでもなくスカラー量も座標変換に関して不変ですが、そもそも$0$階のテンソルなので反変成分とか共変成分とかの区別はありません。 ↩
共変基底ベクトル$e _ i$は$e _ i \in V$なのでその線形結合は$V$の元でしかありえませんし、反変基底ベクトルの線形結合も同様に双対ベクトル空間$V ^ \ast$の元でしかありえません。わかりやすく言えば列ベクトルの線形結合で行ベクトルは作れませんし、その逆も然りということです。物理の人はあまり気にしないみたいですが、厳密にはベクトル$v$を「反変基底で展開したり共変基底で展開したり」することはできないため、必要に応じてベクトルを双対空間に写す必要があります。 ↩
ユークリッド空間以外の空間で加速度ベクトルについて議論するには「解析接続」という操作が必要になり、今回の記事の内容を超えてしまうのでこれはまたの機会としましょう。 ↩
この記事では触れませんが、全微分が不変量であることは、より発展的な「外微分」の概念へとつながっていくことになります。 ↩

数学勉強ノート（座標変換と反変性・共変性・不変量）〜〜関数解析、多様体、解析力学への準備〜〜

概要

参考