pythonで近似式の計算

近似式の計算

numpyによる方法

polyfit

import numpy as np
np.polyfitを利用
np.polyfit(x,y,1)で1次近似，１を変えることで，次数を変えた計算ができる。
np.poly1d(np.polyfit(x, y, 1))で関数が生成される。
np.poly1d(np.polyfit(x, y, 1))(引数)で引数による数値が計算される。

import numpy as np
from matplotlib import pyplot as plt

x= np.linspace(-10,10,20)
y= x**3 +  2*x**2 + 3*x + 10+ np.random.randn(20)*50

#近似式の係数
res1=np.polyfit(x, y, 1)
res2=np.polyfit(x, y, 2)
res3=np.polyfit(x, y, 3)
#近似式の計算
y1 = np.poly1d(res1)(x) #1次
y2 = np.poly1d(res2)(x) #2次
y3 = np.poly1d(res3)(x) #3次

#グラフ表示
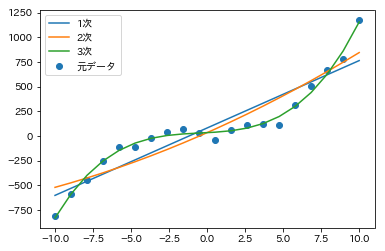
plt.scatter(x, y, label='元データ')
plt.plot(x, y1, label='1次')
plt.plot(x, y2, label='2次')
plt.plot(x, y3, label='3次')
plt.legend()
plt.show()

計算結果

scipyによる方法

leastsqによる近似

from scipy import optimize
関数を定義して，optimize.leastsq(func1, param1, args=(x, y))で係数を求める。

from scipy import optimize

# 1次式の近似
def func1(param,x,y):
    residual = y - (param[0]*x + param[1])
    return residual
param1 = [0, 0]
res_leas1 = optimize.leastsq(func1, param1, args=(x, y))#係数
# 2次式の近似
def func2(param,x,y):
    residual = y - (param[0]*x**2 + param[1]*x + param[2])
    return residual
param2 = [0, 0, 0]
res_leas2 = optimize.leastsq(func2, param2, args=(x, y))

# 3次式の近似
def func3(param,x,y):
    residual = y - (param[0]*x**3 + param[1]*x**2 + param[2]*x + param[3])
    return residual
param3 = [0, 0, 0, 0]
res_leas3 = optimize.leastsq(func3, param3, args=(x, y))

curve_fitによる近似

from scipy import optimize
関数を定義して，optimize.curve_fit(func_c1, x, y)で係数を求める。

from scipy import optimize

# 1次式の近似
def func_c1(x, a, b):
    return a*x + b
res_c1 = optimize.curve_fit(func_c1, x, y)#係数

# 2次式の近似
def func_c2(x, a, b, c):
    return a*x**2 + b*x + c
res_c2 = optimize.curve_fit(func_c2, x, y)

# 3次式の近似
def func_c3(x, a, b, c, d):
    return a*x**3 + b*x**2 + c*x +d
res_c3 = optimize.curve_fit(func_c3, x, y)