この記事は量子コンピューター Advent Calendar 2020の二日目の記事です。
はじめに
@wotto27octと申します.ふだんはテンソルネットワークについてあれこれ考えています.
この記事では,テンソルネットワークと呼ばれる枠組みを用いた量子回路のシミュレーションについて説明します.量子回路をテンソルネットワークとみなして計算することで,回路によってはナイーブに計算するより高速に計算できます.
テンソルネットワークを用いた量子回路のシミュレーションは,例えばGoogleの量子プロセッサSycamoreが200秒で実行できる計算を,スパコンではどのくらいの時間で計算できるのかを推測するのにも用いられています.
テンソルネットワークについては,例えばこのページを参照してください.
量子回路のシミュレート
ここに$|\psi_1\rangle$〜$|\psi_4\rangle$は入力の状態(直積集合),$U_1$〜$U_3$はユニタリ回路,$M$は一番下のqubitを測定する物理量とします.
この回路で得られる物理量の期待値を計算するには,入力状態に次々にユニタリ行列をかけていき,最後に得られた状態$|\psi_{final}\rangle$に対して1〜3qubit目のpartial traceを取ったあと物理量$M$の左右から挟めばいいです.式で書くと
\langle \psi_{final}|I_3\otimes M|\psi_{final}\rangle
となります.コードで書くと以下のようになります.
import numpy as np
from scipy.stats import unitary_group
import time
init_state = [None for i in range(4)]
dim = 2
for i in range(4):
init_state[i] = np.random.randn(dim) + 1j*np.random.randn(dim)
init_state[i] /= np.linalg.norm(init_state[i])
Us = [None for i in range(3)]
for i in range(3):
Us[i] = unitary_group.rvs(dim**2)
A = np.random.randn(dim, dim) + 1j*np.random.randn(dim, dim)
m = (A + A.T.conj()) / 2.0
state = np.einsum("i,j,k,l->ijkl", *init_state).reshape(dim**4)
U0 = np.einsum("ij,kl->ikjl", Us[0], np.eye(dim**2)).reshape(dim**4, dim**4)
U1 = np.einsum("ij,kl,mn->ikmjln", np.eye(dim), Us[1], np.eye(dim)).reshape(dim**4, dim**4)
U2 = np.einsum("ij,kl->ikjl", np.eye(dim**2), Us[2]).reshape(dim**4, dim**4)
M = np.einsum("ij,kl->ikjl", np.eye(dim**3), m).reshape(dim**4, dim**4)
start = time.time()
final_state = np.dot(U2, np.dot(U1, np.dot(U0, state)))
true_expectation = np.einsum("i,ij,j", final_state.conj(), M, final_state)
end = time.time()
print("expectation:", true_expectation, "elapsed time:", end - start)
テンソルネットワークを用いた量子回路の表現
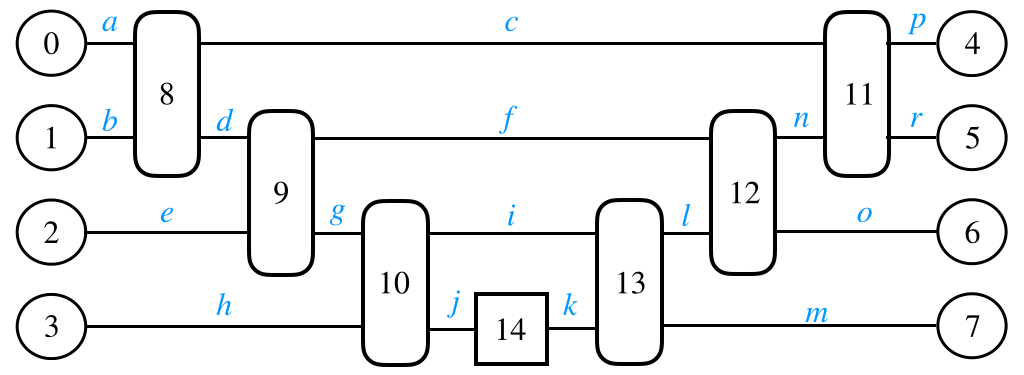
量子回路の期待値をとる操作をテンソルネットワークの枠組みで表すと以下のようになります.
番号とindexは適当に割り振っています.テンソルネットワークの観点から見ると,量子回路の期待値を取る操作は上記のテンソルネットワークの全体を縮約をとることに対応します.
理想的な縮約の順番を計算する
テンソルネットワークで表現しただけでは計算時間は早くなりません.グラフ理論の知識を用いて上記のテンソルネットワークを効率的に計算できる縮約の順番を計算しなければなりません.ところが,最適な縮約の順番を計算する問題はNP-hardであることが知られています.
今回はテンソル数が少ないので,動的計画法を用いてゴリ押しで最適な順番を計算してみましょう.さらに簡単のため,全ての辺は同じ次元を持つと仮定します.
アルゴリズムを以下に示します.ただし,ネットワーク$\mathcal{N}$に対して,$\mathrm{cost}$はネットワークを縮約するときのコスト,$\mathcal{Q}$はネットワークを縮約する順番を指します.$\mathcal{Q}$について,例えば$((0,1),2)$は,テンソル0と1の縮約を取ったあとにテンソル2と縮約を取る,という意味になります.
- もしネットワーク$\mathcal{N}$について最適なコストと縮約の順番を既に計算してあれば,その値を返します.
- ネットワーク$\mathcal{N}$がひとつのテンソル$T$からなれば,$\mathrm{cost}=0$,$\mathcal{Q}=T$として返します.
- ネットワーク$\mathcal{N}$を2つのサブネットワーク$\mathcal{N_1}$,$\mathcal{N_2}$に分けます.
4. ネットワーク$\mathcal{N_1}$のコスト$\mathrm{cost_1}$と縮約の順番$\mathcal{Q}1$を再帰的に計算します.
5. 同様に,ネットワーク$\mathcal{N_2}$のコスト$\mathrm{cost_2}$と縮約の順番$\mathcal{Q}2$を再帰的に計算します.
6. ネットワーク$\mathcal{N_1}$の縮約をとったテンソルを$T_1$,$\mathcal{N_2}$の縮約をとったテンソルを$T_2$とおいたとき,$T_1$と$T_2$の縮約をとったときのコストを$\mathrm{cost{contract}}$とします.
7. もし,$\mathrm{cost_1}+\mathrm{cost_2}+\mathrm{cost{contract}}$の値が今までの値より小さければ,$\mathrm{cost}=\mathrm{cost_1}+\mathrm{cost_2}+\mathrm{cost_{contract}}$として,$\mathcal{Q}=(\mathcal{Q}_1,\mathcal{Q}_2)$とします. - 以上で得られた$\mathrm{cost}$,$\mathcal{Q}$を記録して返します.
この動的計画法は指数時間かかりますが,今回は$n=15$なので十分計算できます.$n$の値がより大きくなると,近似法を用いて縮約の順番を計算することになります.
以下にソースコードを示します.
import itertools
class Node:
def __init__(self, left, right, tensor, index, cost, name):
self.parent = -1
self.left = left
self.right = right
self.tensor = tensor
self.index = index
self.cost = cost
self.name = name
self.cont_str = None
def calc_tensor(self):
if self.tensor is not None:
return self.tensor
self.left.calc_tensor()
self.right.calc_tensor()
left_str = "".join([str(i) for i in self.left.index])
right_str = "".join([str(i) for i in self.right.index])
node_str = "".join([str(i) for i in self.index])
self.cont_str = left_str + "," + right_str + "->" + node_str
self.tensor = np.einsum(self.cont_str, self.left.tensor, self.right.tensor)
return self.tensor
def calc_expression(self):
if self.left is None:
return str(self.name)
left = self.left.calc_expression()
right = self.right.calc_expression()
return "(" + left + "," + right + ")"
def dp(N):
if N in mu_best:
return mu_best[N], Q_best[N]
if len(N) == 1:
mu_best[N] = 0
N_idx = N[0]
node = Node(None, None, tensor_list[N_idx], index_list[N_idx], 0, str(N_idx))
Q_best[N] = node
return 0, node
for i in range(1, len(N)//2 + 1):
left_div_list = tuple(itertools.combinations(list(N), i))
for left_div in left_div_list:
right_div = tuple([j for j in list(N) if j not in left_div])
L_cost, LQ = dp(left_div)
R_cost, RQ = dp(right_div)
common_index = set(LQ.index) & set(RQ.index)
contract_cost = 2 ** (len(LQ.index) + len(RQ.index) - len(common_index))
if N not in mu_best or mu_best[N] > L_cost + R_cost + contract_cost:
mu_best[N] = L_cost + R_cost + contract_cost
index = [x for x in dict.fromkeys(LQ.index + RQ.index) if (LQ.index + RQ.index).count(x) == 1]
Q_best[N] = Node(LQ, RQ, None, index, mu_best[N], None)
return mu_best[N], Q_best[N]
はじめの量子回路の期待値を計算してみましょう.ただし,各テンソルのindexの順番と,adjointのテンソルは複素共役を取らないといけないことに注意します.
mu_best = {}
Q_best = {}
tensor_list = []
index_list = []
for i in range(4):
tensor_list.append(init_state[i])
index_list.append(["a"])
index_list.append(["b"])
index_list.append(["e"])
index_list.append(["h"])
for i in range(4):
tensor_list.append(init_state[i].conj())
index_list.append(["p"])
index_list.append(["r"])
index_list.append(["o"])
index_list.append(["m"])
for i in range(3):
tensor_list.append(Us[i].T.reshape(dim,dim,dim,dim))
index_list.append(["a", "b", "c", "d"])
index_list.append(["d", "e", "f", "g"])
index_list.append(["g", "h", "i", "j"])
for i in range(3):
tensor_list.append(Us[i].conj().reshape(dim,dim,dim,dim))
index_list.append(["c", "n", "p", "r"])
index_list.append(["f", "l", "n", "o"])
index_list.append(["i", "k", "l", "m"])
tensor_list.append(m)
index_list.append(["k", "j"])
all = tuple([i for i in range(15)])
dp(all)
top = Q_best[all]
start = time.time()
top.calc_tensor()
end = time.time()
print("expectation by tensor network", top.tensor, "elapsed time by tensor network", end - start)
print("contraction order", top.calc_expression())
結果
expectation: (-0.3977229947914339+4.9060148304969076e-17j) elapsed time: 7.772445678710938e-05
expectation by tensor network (-0.3977229947914338+0j) elapsed time by tensor network 0.0001628398895263672
contraction order (0,(1,(8,((11,(4,5)),((2,9),((6,12),((3,10),(14,(7,13)))))))))
縮約の順番と結果は正しく計算されているようですが,どうやらテンソルネットワークを使うよりもナイーブに計算したほうが速そうです.テンソルネットワークの縮約は込み入った計算になるため,単純な行列の掛け算に計算速度で負けてしまう逆転現象がしばし起きます.
例えば上のコードにおいてdim=4としてみるとどうなるでしょう.
expectation: (0.961459166797361+1.588356182691264e-17j) elapsed time: 0.0009388923645019531
expectation by tensor network (0.9614591667973607+2.7755575615628914e-17j) elapsed time by tensor network 0.00018739700317382812
contraction order (0,(1,(8,((11,(4,5)),((2,9),((6,12),((3,10),(14,(7,13)))))))))
今度はテンソルネットワークを用いたほうが高速になりました.実は上記のような回路は,最適な計算時間は$O(nd^5)$程度であることを示すことができます.ナイーブな計算時間は$O(nd^{8})$ですので,次元を上げていけばいくほどテンソルネットワークを用いたほうが計算時間が短くなります.さらに,テンソル縮約の順番の計算は次元に依存しません.
まとめ
量子回路の期待値をテンソルネットワークを用いて計算する方法を説明しました.
テンソルネットワークのためのPythonライブラリだと,googleのtensornetworkが有名です.このライブラリには,最適な縮約の順番を高速に求めるNCONというライブラリが付属しています.
テンソルネットワークの縮約の順番を近似的に求めるライブラリとして,opt_einsumがあります.numpyのnp.einsumと同じように使うことができ便利です.
また,現在QTensorNetというライブラリを開発中です.このライブラリを用いることで,量子回路の期待値をテンソルネットワーク・バックエンドで簡単に求めることができます.また,量子機械学習への応用を簡単に行うことができます.
参考文献
Faster identification of optimal contraction sequences for tensor networks