この記事は量子コンピューター Advent Calendar 2022の一日目の記事です。
$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
wottoです.今日は,最近界隈をちょっと賑わせた論文"The Quantum Fourier Transform Has Small Entanglement"について論文紹介したいと思います.主張としては,
- 量子フーリエ変換はMPO(Matrix Product Operator)と呼ばれるテンソルネットワークで効率的に記述できる
- 上記のMPOを用いることで,低エンタングルメントの入力に対する離散フーリエ変換をFFTより高速に実行できる
というものです.
以下,数式や図は全て上の論文に準拠しています.
量子フーリエ変換
量子フーリエ変換は,量子状態の振幅に対し離散フーリエ変換を施す操作で,以下のユニタリ演算子で記述できます.$n$は量子ビット数です.
$$
F_n=\frac{1}{\sqrt{2^n}}\sum_{q=0}^{2^n-1}\sum_{q'=0}^{2^n-1}e^{i2\pi qq'/2}\ket{q}\bra{q'}
$$
$q$を2進数表示$q=q_1q_2\cdots q_n$で表すと,次のように書き表すこともできます.
$$
F_n\ket{q_1q_2\cdots q_n}=\frac{1}{\sqrt{2^n}}(\ket{0}+e^{2\pi i0.q_n}\ket{1})\otimes(\ket{0}+e^{2\pi i0.q_{n-1}q_n}\ket{1})\otimes\cdots(\ket{0}+e^{2\pi i0.q_1q_2\cdots q_n}\ket{1})
$$
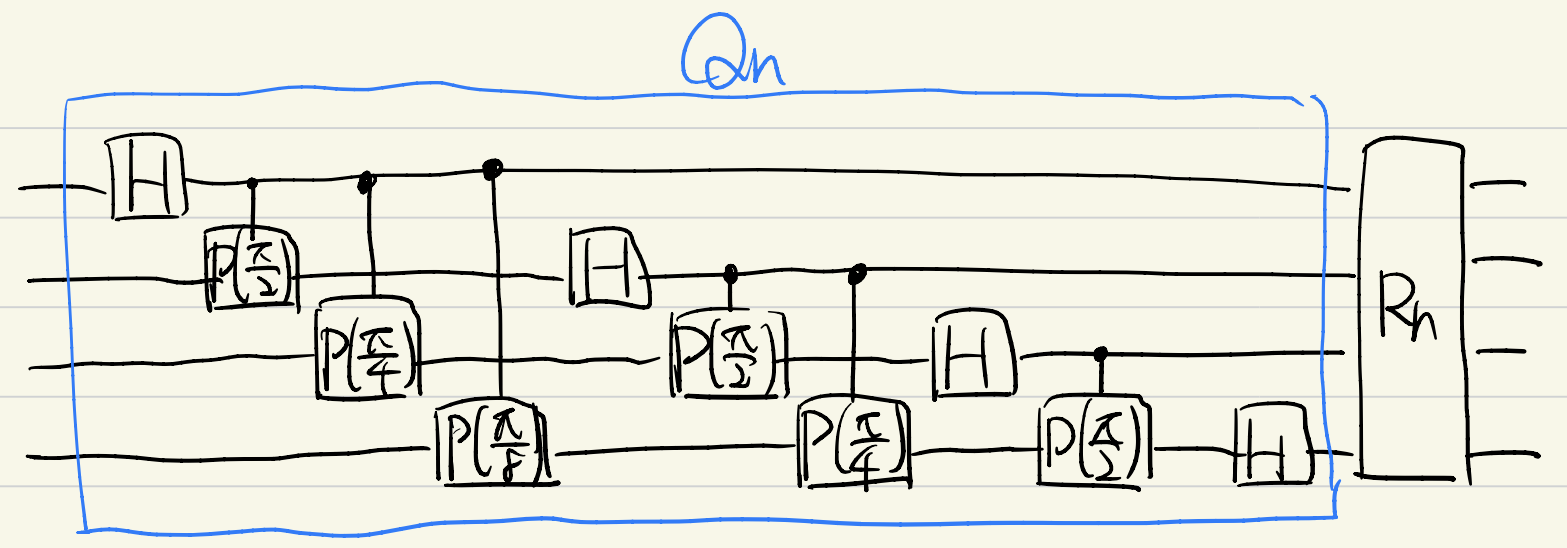
量子フーリエ変換は図のような量子回路$F_n=R_n\cdot Q_n$で実現できます.ただし
P(\theta)=
\begin{pmatrix}
1 & 0 \\
0 & e^{i\theta}
\end{pmatrix}
$R_n$はqubit reversal:$R_n\ket{q_1\cdots q_n}=\ket{q_n\cdots q_1}$で,例えばLNNアーキテクチャ(最近接の量子ビットにのみ2量子ビットゲートをかけられる)で実装するには深さ$O(n)$,2量子ビットゲート数$O(n^2)$の密な回路が必要であることが知られており,強いエンタングルメントが発生してしまいます.
$Q_n$は量子フーリエ変換のqubit reversalを取る前までの演算子で,以下のように作用します.
$$
Q_n\ket{q_1q_2\cdots q_n}=\frac{1}{\sqrt{2^n}}(\ket{0}+e^{2\pi i0.q_1q_2\cdots q_n}\ket{1})\otimes(\ket{0}+e^{2\pi i0.q_2\cdots q_n}\ket{1})\otimes\cdots(\ket{0}+e^{2\pi i0.q_n}\ket{1})
$$
この$Q_n$の部分が,以下のようなMPO(Matrix Product Operator)と呼ばれるテンソルネットワークで効率的に表現できることを示したのが,今回紹介している論文のメインの定理になります.

演算子の二分Schmidt係数
系$\mathcal{A},\mathcal{B}$に作用するユニタリ演算子について,以下のような特異値分解を考えます.
$$
U=\sqrt{N}\sum_{k=1}^{\chi}\sigma_k A_k\otimes B_k
$$
ここで$\sigma_k$はSchmidt係数と呼ばれ,降順に並んでおり,非負の値を取ります.$\chi$はSchmidtランクと呼ばれ,最大で$min(dim(\mathcal{A})^2,dim(\mathcal{B})^2)$となります.図で書くと以下のようになります.ただし三角のテンソルはIsometryを表します.

もしSchmidtランクが$\chi$のとき,演算子$U$はボンド次元$\chi$のMPOで表すことができます.
そうでなくても,例えばSchmidt係数が指数的に減衰する場合,多くのSchmidt係数は無視できるほど小さくなります.十分大きなボンド次元$\chi'<\chi$を取ることで,MPOで精度良く近似することができます.
$$
U=\sqrt{N}\sum_{k=1}^{\chi}\sigma_k A_k\otimes B_k\simeq\sqrt{N}\sum_{k=1}^{\chi'}\sigma_k A_k\otimes B_k
$$
よって,演算子がMPOで精度良く表現できるかどうかは,演算子を二分したときのSchmidt係数の分布に依存します.
$Q_n$のSchmidt係数の分布
$Q_n$をじっと睨むと,系$\mathcal{A}$を量子ビット$1$〜$j$番目,系$\mathcal{B}$をそれ以外としたときのSchmidt係数は,以下のような行列:
$$
T_{n,j}=\frac{1}{2^n}\sum_{x,y}\omega_{n,j}^{x-y}\frac{\sin{(\pi(x-y)/2^j)}}{\sin{(\pi(x-y)/2^n)}}\ket{x}\bra{y}
$$
の固有値に対応しています.さらに変形すると,以下のようなperiodic discrete prolate spheroidal sequences(P-DPSSs)と呼ばれる固有方程式に属することがわかります.
$$
\frac{1}{N}\sum_{y=0}^{N'-1}\frac{\sin{(2W\pi(x-y))}}{\sin{(\pi(x-y)/N)}}v_{N,N',W}^{k,y}=\lambda_{N,N',W}^k v_{N,N',W}^{k,x}
$$
今回のケースでは$N=2^n,N'=2^j,2W=1/2^j$です.このような固有方程式の解(固有値)の上界についてはよく研究されているらしく,それらの結果を用いると,$k\gt 4$においてSchmidt係数は
$$
\sigma^k\leq\sqrt{2}\exp\left(-\frac{2k+1}{2}\log\left(\frac{4k+4}{e\pi}\right)\right)
$$
となり,$k$に対して指数的に落ちることがわかるらしいです.へー.
$Q_n$のSchmidt係数の分布(直感)
上の説明は素晴らしいのですがさっぱり分からんので,なんとか直感的な解釈もしてみたいと思います.
$$
Q_n\ket{q_1q_2\cdots q_n}=\frac{1}{\sqrt{2^n}}(\ket{0}+e^{2\pi i0.q_1q_2\cdots q_n}\ket{1})\otimes(\ket{0}+e^{2\pi i0.q_2\cdots q_n}\ket{1})\otimes\cdots(\ket{0}+e^{2\pi i0.q_n}\ket{1})
$$
$Q_n$の表式をもう一度よく見てみると,例えば1量子ビット目の出力$(\ket{0}+e^{2\pi i0.q_1q_2\cdots q_n}\ket{1})$は$q_1,q_2$などの値には大きく影響しますが,例えば$q_n$の影響はそれらに比べ指数的に弱いです.例えば$n$が十分大きいとき,$n$量子ビット目の情報など,$1$量子ビット目の出力には全く影響しないことが予想できます.
これらを総合的に鑑みると,おそらく$i$番目の量子ビットの情報はその左右有限個の量子ビットくらいにしか実質的には影響していないのではないかと考えられます.その結果,$Q_n$は有限のボンド次元しか持たないMPOでも十分に記述できるのだ,くらいが定性的な説明になるかと思います.
量子インスパイアド離散フーリエ変換への応用
量子フーリエ変換をMPOで表すことができた,というだけで(テンソルネットワークの人たちにとっては)嬉しいのですが,さらに量子インスパイアドアルゴリズムとして応用することができます.
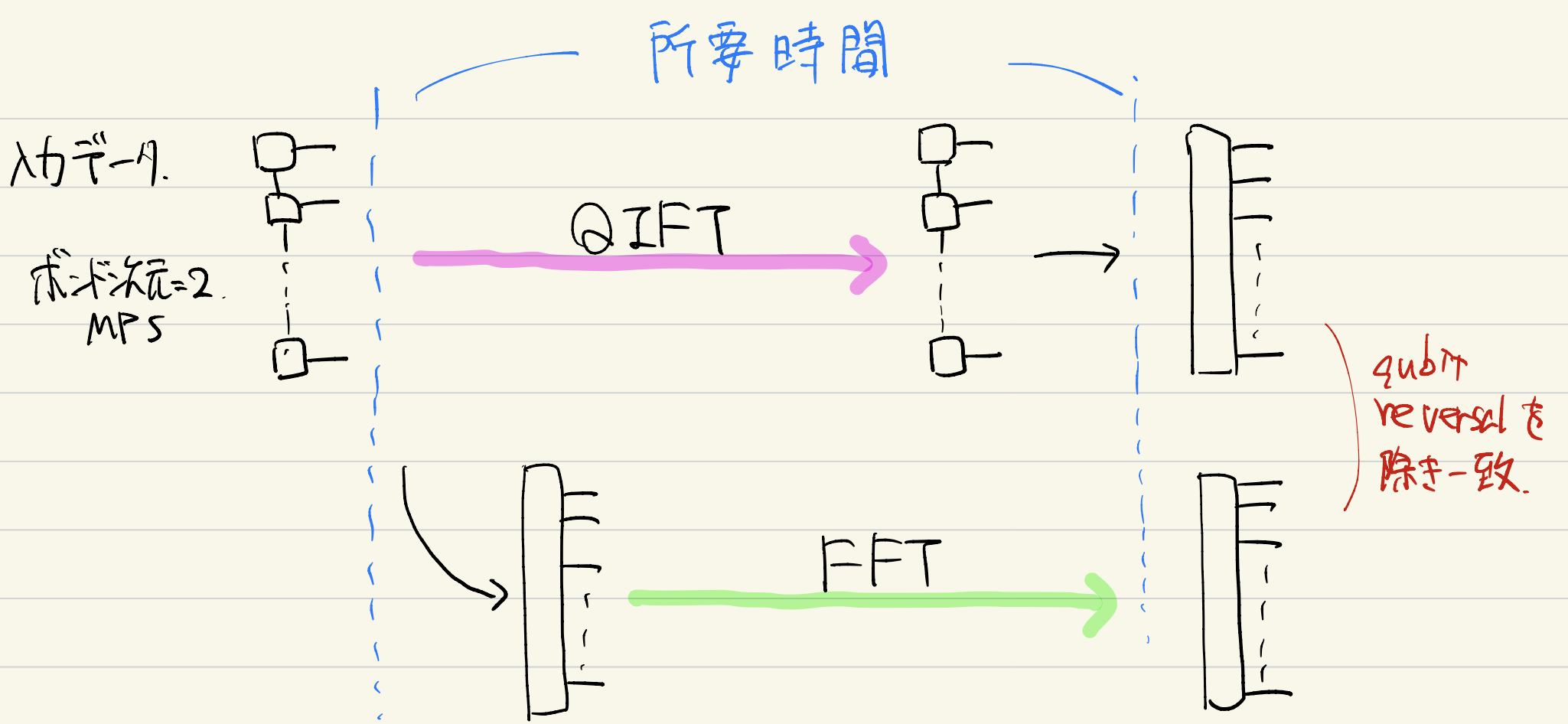
(正規化された)長さ$2^n$のデータがボンド次元$d$のMPS表現を持つとします.このデータを離散フーリエ変換したいとき,例えばFFTを用いると$O(n2^n)$かかりますが,量子インスパイアド離散フーリエ変換(以下QIFTと記す)を用いれば$poly(n,d)$で実行することができます(ただし出力はMPS).

MPSを状態ベクトルに変換することでデータ列自体も手に入れることができます.この操作には結局指数時間かかりますが,それでも入力がMPSで表される場合,QIFTを経由した方が高速になります.
考察
量子コンピュータ要らないの?
今回の量子インスパイアド離散フーリエ変換では入力が低エンタングルメント状態のとき$poly(n)$で実行できましたが,量子コンを用いた量子フーリエ変換では任意の入力に対し$poly(n)$で実行できます.ただしもちろん,振幅の情報をそのまま読み出すことはできません.
既によく知られた話では?
不勉強のため恥ずかしながら自分はこの論文を読むまで知らなかったのですが,調べていくと確かに似たような話がいくつかあります.
例えば2007年の論文では,product stateに対し量子フーリエ変換した状態からサンプリングするのに,制御ゲートを測定+古典分岐に置き換えることで効率的に古典シミュレートできることを示しています.MPSへの拡張は自明ですが,今回のように量子状態そのものを得る方がシミュレーションとしては強いです.
また,いくつかの先行研究12では,superfast Fourier transformという呼び方で,量子フーリエ変換にインスパイアされた古典アルゴリズムが提唱されているらしいですが,量子フーリエ変換の演算子そのものを厳密にMPO表示できることは利用していません.
今回の論文で得られた最も興味深いポイントは,離散フーリエ変換という実用上有意義な線形変換が低エンタングルメント構造を持ち,有限のボンド次元を持つMPOで表されることを厳密に示したことにあると思います.テンソルネットワークを用いた情報処理は近年研究が盛んに行われており,例えばニューラルネットワークの線形層の圧縮,偏微分方程式の求解など,さまざまな用途への応用が期待されています.ただ,元々テンソルネットワークは計算物理学の文脈において波動関数など量子状態を表現するのに導入された概念で,必ずしも古典的な情報をうまく取り扱える(=圧縮できる)とは限らず,ある程度はヒューリスティックに頼る傾向にもあります.今回の研究を発端に,実世界のデータの低エンタングル構造をうまく活用した量子インスパイアドアルゴリズムがさらに発達するのではないかと期待しています.
量子インスパイアド離散フーリエ変換の実装
最後に,簡単にQIFTの実装とそれを用いた数値実験を紹介して終わろうと思います.アルゴリズムの詳細は元論文を参照していただきたく思います.numpyとopt_einsumしか使っていないPythonベタ書きコードなので,ここからダウンロードしていただくと手元でも試せると思います.
主要部について載せます.
def prepare_MPO(n):
if n == 1:
MPO = [np.array([[1,1],[1,-1]]).astype(np.complex128).reshape(2,2,1,1) / np.sqrt(2)]
return MPO
MPO = [copy_H()]
for i in range(1, n-1):
MPO.append(order4_Phase(np.pi/(2**i)))
MPO.append(order3_Phase(np.pi/(2**(n-1))))
return MPO
↑で,量子フーリエ変換のうち,$i$番目の量子ビットにかけるアダマールゲートと,$i$番目を制御ビットとする制御位相ゲートをまとめて一つのMPOとして準備します.
def contract_MPO(MPO1, MPO2, chi):
newMPO = []
cdim, gdim = MPO1[-1].shape[2], MPO2[-1].shape[2]
bottom = oe.contract("abcd,eagh->gcebdh", MPO1[-1], MPO2[-1]).reshape(-1, 4)
U, s, Vh = np.linalg.svd(bottom, full_matrices=False)
if len(s) < chi:
newMPO.append(Vh.reshape(-1,2,2,1).transpose(1,2,0,3))
tmp = np.dot(U, np.diag(s)).reshape(gdim, cdim, -1)
else:
newMPO.append(Vh[:chi].reshape(-1,2,2,1).transpose(1,2,0,3))
tmp = np.dot(U[:,:chi], np.diag(s[:chi])).reshape(gdim, cdim, -1)
for i in range(1, len(MPO2)):
dimi = tmp.shape[2]
cdim, gdim = MPO1[-1-i].shape[2], MPO2[-1-i].shape[2]
tmp = oe.contract("abcd,eagh,hdi->gcebi", MPO1[-1-i], MPO2[-1-i], tmp).reshape(-1, 4*dimi)
U, s, Vh = np.linalg.svd(tmp, full_matrices=False)
if len(s) < chi:
newMPO.append(Vh.reshape(-1,2,2,dimi).transpose(1,2,0,3))
tmp = np.dot(U, np.diag(s)).reshape(gdim, cdim, -1)
else:
newMPO.append(Vh[:chi].reshape(-1,2,2,dimi).transpose(1,2,0,3))
tmp = np.dot(U[:,:chi], np.diag(s[:chi])).reshape(gdim, cdim, -1)
dimd = newMPO[-1].shape[3]
newMPO[-1] = oe.contract("abcd,efc->abefd", newMPO[-1], tmp).reshape(2,2,-1,dimd)
# move apex to bottom
for i in range(len(MPO2)-1):
dimc, dimd = newMPO[-1-i].shape[2], newMPO[-1-i].shape[3]
tmp = oe.contract("abcd,efdg->abcefg", newMPO[-1-i], newMPO[-2-i]).reshape(4*dimc,-1)
U, s, Vh = np.linalg.svd(tmp, full_matrices=False)
newMPO[-1-i] = U[:,:dimd].reshape(2,2,dimc,dimd)
newMPO[-2-i] = np.dot(np.diag(s[:dimd]), Vh[:dimd]).reshape(dimd,2,2,-1).transpose(1,2,0,3)
return MPO1[:len(MPO1) - len(MPO2)] + newMPO[::-1]
↑で2つのMPOを1つのMPOにまとめています.この操作には標準形(canonical form)と呼ばれる,テンソルネットワークでよく使われている手法を使用しています.
def convert_QFT_to_MPO(n, chi):
MPO1 = prepare_MPO(n)
for i in range(1, n):
MPO2 = prepare_MPO(n-i)
MPO1 = contract_MPO(MPO1, MPO2, chi)
return MPO1
$n$個全てのMPOを1つのMPOにすることで,所望のMPO($Q_n$のMPO表現)が得られました.
def qift(MPS, QFT_MPO):
"""Quantum-inspired Fourier Transformation
Args:
MPS (List[np.array]) : the input MPS. Each tensor has a shape (2, *, *)
QFT_MPO(List[np.array]) : the MPO that represents Q_n in QFT
Return:
MPS (List[np.array]) : the result MPS.
"""
n = len(MPS)
if MPS[0].shape[1] != 1:
raise ValueError("the left dimension of MPS must be 1.")
if MPS[-1].shape[2] !=1:
raise ValueError("the right dimension of MPS must be 1.")
for i in range(n-1):
if MPS[i].shape[2] != MPS[i+1].shape[1]:
raise ValueError(f"the bond dimension between {i} and {i+1} differs.")
res = []
for i in range(n):
left_dim = QFT_MPO[i].shape[2] * MPS[i].shape[1]
res.append(oe.contract("abcd,bef->acedf", QFT_MPO[i], MPS[i]).reshape(2, left_dim, -1))
return res
あとは,MPSとして表された入力と,MPOとして表された$Q_n$の縮約を取ることで,離散フーリエ変換後のMPSを得ることができます.
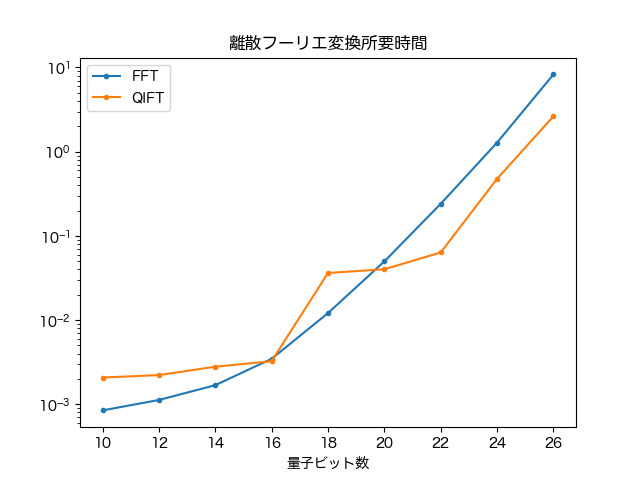
QIFTがどの程度のパフォーマンスを発揮するか調べるため,numpyのfft関数と以下のような設定で時間比較しました.
結果は以下のようになりました.
量子ビット数の多いところではnumpyのfftよりQIFTの方が高速に動作しました.が,思ったほど高速ではなかったです.QIFTの最も重い部分がMPSから状態ベクトルに変換する箇所で,そこは並列化などを工夫すればより高速になるので,まぁこんなもんかなぁとも思います.いずれにせよ,自分の適当実装でもnumpyのfftより高速に動作させることができました.