はじめに
データ構造の多くは、破壊的な操作を提供しています。例えば配列はある要素を別の値に更新する操作を提供しています。配列の更新操作の処理時間は配列の長さや値に依存しないという点で優れています。
一方で、データ構造に対して非破壊的な操作を実行したい場面もあるかと思います。例えば配列を累積値とするreduce/fold処理(畳み込み演算)の各計算においては非破壊的に新しい配列を生成すべきです(破壊後の配列を計算結果とすることも可能ですが健全な使い方とは言い難いでしょう)。あるいはReactのステートフックのstate更新のように更新後のオブジェクトを新たにセットする必要がある場合、下記のように非破壊的に新しくオブジェクトを生成しそれをセットさせることになります。
const [items, setItems] = useState([3, 1, 4, 1, 5, 9, 2]);
// itemsに要素を1個追加するだけなのに、itemsの要素数に比例する計算時間がかかる
setItems(state => ([ ...state, 2019]));
非破壊的な操作を愚直に実装すると処理時間が大きくなってしまいます。たとえ一つの要素だけ変更する場合でも、それ以外の要素も含めて新しい配列を生成する必要があるからです。したがって、下記のNGコードの気持ちで書きたくなります。
const [items, setItems] = useState([3, 1, 4, 1, 5, 9, 2]);
// NG!! stateに破壊的操作を加えるのはダメ(定数時間で追加したい気持ち)
setItems(state => state.push(2019));
高速かつ非破壊的にデータを更新できないのでしょうか。
1操作あたりの差分が小さい場合、直観的にはそれ以外のデータを使いまわすことで効率化できるように思えます。
永続データ構造 はこのアイデアに基づいて非破壊的な操作を提供するデータ構造です。
問題: 配列のバージョン管理
永続データ構造が有効であるケースとして、本記事では配列のバージョン管理に関する問題を扱います。
問題文
配列 $A$ が与えられます。 $A$ の初期バージョン名は a.0 です。
あなたは、あるバージョンの $A$ のある要素の値を他の値に更新した配列に新しいバージョン名を付与する、という更新操作を何回か実行しました。
すべての更新操作を実行後、あなたは以下のクエリを処理したくなりました。
指定したバージョンの $A$ の $i$ 番目の要素は何か?
上記のクエリが複数個与えられるので、それぞれに回答してください。
ただし、配列は0-indexedとします(先頭の要素を0番目と数えることにします)。
例
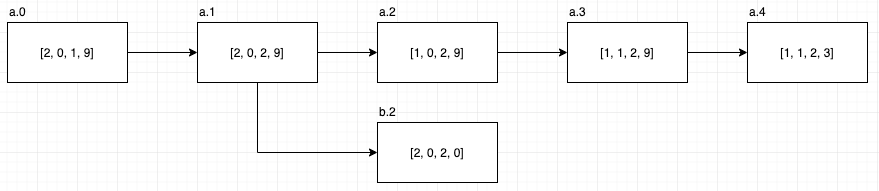
$A = [2, 0, 1, 9]$ とします。
以下の更新操作を順に実行した場合を考えます。
| 更新対象バージョン | 更新対象インデックス | 更新後の値 | 更新後のバージョン |
|---|---|---|---|
| a.0 | 2 | 2 | a.1 |
| a.1 | 0 | 1 | a.2 |
| a.2 | 1 | 1 | a.3 |
| a.1 | 3 | 0 | b.2 |
| a.3 | 3 | 3 | a.4 |
配列のバージョンツリーは以下となります。
このとき、クエリとクエリの回答例は以下の通りです。
| クエリ対象バージョン | クエリ対象インデックス | 回答 |
|---|---|---|
| a.1 | 2 | 2 |
| a.4 | 1 | 1 |
| a.4 | 3 | 3 |
| b.2 | 3 | 0 |
効率的なオフラインアルゴリズム
オフラインアルゴリズム とは(クエリを含めて)事前にすべての入力データにアクセス可能な状態で問題を解くアルゴリズムです。バッチ処理と考えてもよいでしょう。
これに対して、事前にすべての入力データにアクセスできず、先頭から順に処理して問題を解くアルゴリズムを オンラインアルゴリズム と言います。まずは上記の問題をオフラインアルゴリズムで効率的に解く方法を考えてみます。
クエリごとにそのバージョンにおける配列の状態を追いかけると大きな時間がかかりそうです。
そこで、クエリを先読みし、各バージョンに対するクエリをひとまとめにして無駄を省きましょう。
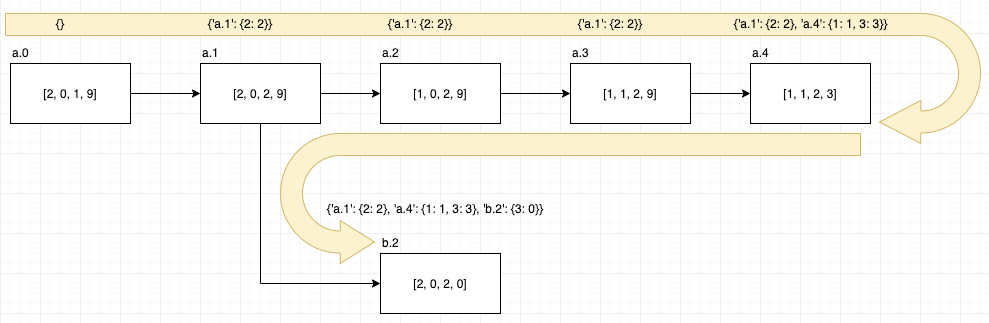
バージョンa.0から順に深さ優先探索で各バージョンを走査しながらそのバージョンに対する(まとめられた)クエリに回答することで、操作の個数とクエリの個数に関して線形時間ですべてのクエリに回答できます(オフラインアルゴリズムであることの利が効いています)。
上記のオフラインアルゴリズムをPythonで実装してみます。
まずは入力です。オフラインアルゴリズムなので、最初からすべての更新操作・クエリが与えられます。
# 配列の初期状態
A = [2, 0, 1, 9]
# 更新操作
operations = [('a.0', 2, 2, 'a.1'), ('a.1', 0, 1, 'a.2'), ('a.2', 1, 1, 'a.3'),
('a.1', 3, 0, 'b.2'), ('a.3', 3, 3, 'a.4')]
# クエリ
queries = [('a.1', 2), ('a.4', 1), ('a.4', 3), ('b.2', 3)]
次に、各クエリが対象とするバージョンを辞書型のデータ grouped_queries としてまとめます。
例えば grouped_queries['a.4'] = [1, 3] のように grouped_queries[v] はバージョン v に対するクエリが対象とするインデックスのリストとします。
defaultdictを用いることでそのバージョンを対象とするクエリが存在しない場合は空リストになるようにします(例えば、 grouped_queries['a.3'] = [] です)。
from collections import defaultdict
# クエリを先読みし、バージョンごとにクエリをまとめる
grouped_queries = defaultdict(list)
for version, index in queries:
grouped_queries[version].append(index)
今回のクエリだと grouped_queries = {'a.1': [2], 'a.4': [1, 3], 'b.2': [3]} となります。
次に、各バージョンの走査を効率化するためにバージョンツリー next_versionsを作ります。
例えば、 next_versions['a.1'] = [('a.2', 0, 1), ('b.2', 3, 0)] のように next_versions[v] はバージョンvの次バージョンv'について、タプル(v', v'で変更されるインデックス, 変更後の値)を集めたリストとしています。
こちらもdefaultdictを用いることで次バージョンが存在しない場合は空リストになるようにします(例えば、 next_versions['a.4'] = [] です)。
# バージョンツリーを構築する
next_versions = defaultdict(list)
for version, index, new_value, next_version in operations:
next_versions[version].append((next_version, index, new_value))
今回の変更操作だと next_versions は以下となります。
{'a.0': [('a.1', 2, 2)],
'a.1': [('a.2', 0, 1), ('b.2', 3, 0)],
'a.2': [('a.3', 1, 1)],
'a.3': [('a.4', 3, 3)]}
これで各クエリに対する回答を計算する準備が整いました!
バージョンツリーを深さ優先探索することで、各バージョン間の差分に着目した効率的な更新が可能です(ここで next_versions を使います)。
深さ優先探索でバージョンに訪問した際、 grouped_queries を参照し、そのバージョンに対するすべてのクエリの回答メモを作成しておきます(深さ優先探索終了後、回答メモを読み上げるだけの状態にすることが目標です)。
深さ優先探索を再帰関数 compute_answers(version, a, answer) として定義します。
compute_answers(version, a, answer) の処理の流れは以下です。
- バージョン
versionに対する各クエリに回答し、回答メモanswerに回答内容を書き込む - 次バージョン
next_versionに対応する配列の更新操作を実行する(aが更新後の配列になる) - 次バージョン
next_versionについて、compute_answers(next_version, a, answer)を再帰的に呼び出す - 次バージョン
next_versionに対応する配列の更新操作を巻き戻す(aが更新前に配列に戻る) - 他にも次バージョンがあれば 2. に戻る
初期バージョンは 'a.0' なので、最初の呼び出しは compute_answers('a.0', A, answers) とすればよいです (answers は空の辞書とします)。
今回の深さ優先探索をイメージ図にすると以下となります。
これをPythonコードにすると下記のようになります。
# バージョンツリーを深さ優先探索で走査し、各バージョンごとに更新処理を行った後に
# そのバージョンに対するすべてのクエリの回答メモを作成する(この時点ではクエリに対する回答を出力しない)
def compute_answers(version, a, answers):
# version: 処理対象のバージョン
# a: 処理対象のバージョンにおける配列A
# answers: クエリ回答メモ。辞書であり、answers[version][index]はバージョンversionに対するインデックスindexのクエリ回答を表す
# そのバージョンに対するすべてのクエリの回答メモを作成
for index in grouped_queries[version]:
answers[version][index] = a[index]
# 深さ優先探索に基づいて次のバージョンにおけるクエリの回答メモを作成する
for next_version, index, new_value in next_versions[version]:
old_value = a[index]
a[index] = new_value
compute_answers(next_version, a, answers)
a[index] = old_value
answers = defaultdict(dict)
# 初期バージョンはa.0である
# 実行後、answersに各クエリに対する回答メモが作成される
compute_answers('a.0', A, answers)
上記を実行して得られる回答メモは answers = {'a.1': {2: 2}, 'a.4': {1: 1, 3: 3}, 'b.2': {3: 0}} となります。
例えばバージョン 'a.4'における配列の1番目の値は answers['a.4'][1] = 1 のように参照できます。
あとは各クエリに対して回答メモを用いて回答するだけです。
# 各クエリに対して回答メモを用いて実際に回答する
for version, index in queries:
print(f'{version}: A[{index}] = {answers[version][index]}')
ここまでのコードをまとめます。
from collections import defaultdict
# 配列の初期状態
A = [2, 0, 1, 9]
# 更新操作
operations = [
("a.0", 2, 2, "a.1"),
("a.1", 0, 1, "a.2"),
("a.2", 1, 1, "a.3"),
("a.1", 3, 0, "b.2"),
("a.3", 3, 3, "a.4"),
]
# クエリ
queries = [("a.1", 2), ("a.4", 1), ("a.4", 3), ("b.2", 3)]
# クエリを先読みし、バージョンごとにクエリをまとめる
grouped_queries = defaultdict(list)
for version, index in queries:
grouped_queries[version].append(index)
# バージョンツリーを構築する
next_versions = defaultdict(list)
for version, index, new_value, next_version in operations:
next_versions[version].append((next_version, index, new_value))
# バージョンツリーを深さ優先探索で走査し、各バージョンごとに更新処理を行った後に
# そのバージョンに対するすべてのクエリの回答メモを作成する(この時点ではクエリに対する回答を出力しない)
def compute_answers(version, a, answers):
# version: 処理対象のバージョン
# a: 処理対象のバージョンにおける配列A
# answers: クエリ回答メモ。辞書であり、answers[version][index]はバージョンversionに対するインデックスindexのクエリ回答を表す
# そのバージョンに対するすべてのクエリの回答メモを作成
for index in grouped_queries[version]:
answers[version][index] = a[index]
# 深さ優先探索に基づいて次のバージョンにおけるクエリの回答メモを作成する
for next_version, index, new_value in next_versions[version]:
old_value = a[index]
a[index] = new_value
compute_answers(next_version, a, answers)
a[index] = old_value
answers = defaultdict(dict)
# 初期バージョンはa.0である
# 実行後、answersに各クエリに対する回答メモが作成される
compute_answers('a.0', A, answers)
# 各クエリに対して回答メモを用いて実際に回答する
for version, index in queries:
print(f'{version}: A[{index}] = {answers[version][index]}')
実行結果は下記の通りです。
a.1: A[2] = 2
a.4: A[1] = 1
a.4: A[3] = 3
b.2: A[3] = 0
期待通りの結果が得られました!
愚直なオンラインアルゴリズム
クエリを先読みすることで効率的にクエリ回答できることは分かりました。
次にクエリの先読みを行わないオンラインアルゴリズムで解いてみましょう。下記のコードのようにクエリの先読みをせずに各クエリに回答する方法を考えていきます。
# 配列の初期状態
A = [2, 0, 1, 9]
# 更新操作
operations = [('a.0', 2, 2, 'a.1'), ('a.1', 0, 1, 'a.2'), ('a.2', 1, 1, 'a.3'),
('a.1', 3, 0, 'b.2'), ('a.3', 3, 3, 'a.4')]
# 更新操作に対して何かする
# クエリに回答する関数(クエリの先読みはしていない)
# hogeには適切な式を書く
def answer(version, index):
print(f'{version}: A[{index}] = {hoge}')
# クエリ
queries = [('a.1', 2), ('a.4', 1), ('a.4', 3), ('b.2', 3)]
# 各クエリに対してanswer関数を適用して回答する
for version, index in queries:
answer(version, index)
フルバックアップによる実装
まずはおそらく最もシンプルなアイデアであるフルバックアップによるオンラインアルゴリズムを考えます。バージョンが更新されるたびに更新後の配列を新たに作成しそれを保持するという方法です。
各更新操作ごとに配列 $A$ の長さに比例する計算時間がかかります。また更新操作の数だけ配列 $A$ が作成されるので、(更新操作の数)×($A$ の要素数)に比例するメモリを必要とします。
このように更新操作の処理を終えるまでに大きな計算時間とメモリを要しますが、クエリの回答は容易いです(対象バージョンの対象インデックスを参照するだけなので)。
Pythonでの実装例は以下です。
# 配列の初期状態
A = [2, 0, 1, 9]
# 更新操作
operations = [('a.0', 2, 2, 'a.1'), ('a.1', 0, 1, 'a.2'), ('a.2', 1, 1, 'a.3'),
('a.1', 3, 0, 'b.2'), ('a.3', 3, 3, 'a.4')]
# フルバックアップを作成
cache = {'a.0': A}
for version, index, new_value, next_version in operations:
cache[next_version] = [
new_value if i == index else a
for i, a in enumerate(cache[version])
]
# クエリに回答する関数(クエリの先読みはしていない)
def answer(version, index):
print(f'{version}: A[{index}] = {cache[version][index]}')
# クエリ
queries = [('a.1', 2), ('a.4', 1), ('a.4', 3), ('b.2', 3)]
# 各クエリに対してフルバックアップを用いて回答する
for version, index in queries:
answer(version, index)
状態復元による実装
次に状態復元によるオンラインアルゴリズムを考えます。フルバックアップとは逆に更新操作を手抜きする代わりにクエリ回答を頑張るという方針です。
各更新操作をもとに各バージョンについて前のバージョンと更新内容を以下のようにメモしておきます(このとき配列 $A$ に対しては何もしません)。
クエリに対しては対象のバージョンから再帰的に前のバージョンを辿り、対象インデックスを更新している操作を見つけたら、その更新操作の更新後の値を返します。初期バージョンまで辿っても対象インデックスが更新されていない場合については初期状態における $A$ の対象インデックスの値を返せばよいです。
例としてバージョンa.4の $A$ の1番目の値を求めたいとします。
まずは a.4 における更新対象のインデックスを確認します。更新対象のインデックスは3なので前のバージョン a.3 に移動します。
a.3 の更新対象のインデックスは1なので、a.3 更新された値を回答すればよいです。
更新後の値は1なのでクエリに対して1を回答します。
状態復元による処理時間を考えてみましょう。
各更新操作は定数時間で処理可能です。一方でクエリ回答には(最悪の場合で)更新操作の数に比例する計算時間がかかります。
メモリ使用量については優秀で、(配列 $A$ の要素数) + (更新操作の数)に比例する程度です。
Pythonでの実装例は以下です。
# 配列の初期状態
A = [2, 0, 1, 9]
# 更新操作
operations = [('a.0', 2, 2, 'a.1'), ('a.1', 0, 1, 'a.2'), ('a.2', 1, 1, 'a.3'),
('a.1', 3, 0, 'b.2'), ('a.3', 3, 3, 'a.4')]
# バージョンツリーを構築する
# prev_version[v] はバージョンvの前バージョンv'について、タプル(v', vで変更されるインデックス, 変更後の値)
prev_version = dict()
for prev, index, new_value, version in operations:
prev_version[version] = (prev, index, new_value)
# 状態復元によりクエリに回答する関数(クエリの先読みはしていない)
def answer(version, index):
# versionから遡り、index番目の要素を更新した操作を探す
# そのような操作があれば、そのような直近の操作について、変更後の値を返す
# そのような操作がなければ、そのバージョンに至るまでにindex番目の要素は更新されていないので
# 初期状態のindex番目の要素を返す
def trace_element(v):
if v == 'a.0':
return A[index]
else:
prev_v, i, value = prev_version[v]
if i == index:
return value
else:
return trace_element(prev_v)
print(f'{version}: A[{index}] = {trace_element(version)}')
# クエリ
queries = [('a.1', 2), ('a.4', 1), ('a.4', 3), ('b.2', 3)]
# 各クエリに対して状態復元により回答する
for version, index in queries:
answer(version, index)
永続データ構造とは
通常、データ構造に対して更新操作を行うとその状態は変化し変更前の状態は失われます。この特性ゆえ、配列をバージョン管理するためにフルバックアップを取得したり状態復元する必要がありました。
これに対して、変更前の状態も保持するデータ構造を 永続データ構造 と言います。変更前の状態も保持するというとフルバックアップと同じように思えますが、差分情報を上手に管理することで、フルバックアップのように振る舞いつつ効率的にデータ管理できる場合があります。
例えば永続配列はフルバックアップによる実装と状態復元による実装の間をとったようなデータ管理を行います(後で詳しく説明します)。
本記事では効率的な永続データ構造の入門として永続スタックを紹介します。
その後、永続配列を紹介し、冒頭の配列バージョン管理問題をオンラインアルゴリズムで効率的に解きます。
永続スタック
スタックはシンプルに永続化できます。まずはスタックでデータ構造の永続化に入門しましょう。
永続スタックの仕様
スタックとは以下の操作が可能なLast In First Out(LIFO)のデータ構造です。
- push(x): データxをスタックの一番上に格納する
- top(): スタックの一番上にあるデータを返す
- pop(): スタックの一番上のデータを削除する
スタックを永続化してみましょう。永続スタックの場合、先ほどの操作は以下になります。
- push(x): データxをスタックの一番上に格納した後のスタックを返す(このスタックは変化なし)
- top(): スタックの一番上にあるデータを返す
- pop(): スタックの一番上のデータを削除した後のスタックを返す(このスタックは変化なし)
pushとpopが非破壊的な操作になっていることに注意してください。
永続スタックの実装方針
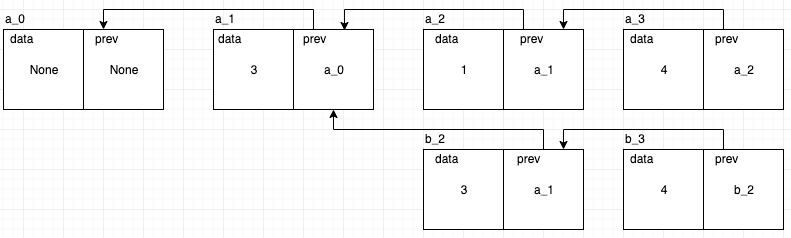
連結リストを用いて全バージョンのデータを管理します。
連結リストの各ノードには二つのデータ(data, prev)を保持させます。
- data: 現バージョンのスタックの一番上のデータ(空の場合はNone)
- prev: 前バージョンのスタックを表すノード(空の場合はNone)
実装のポイントは、連結リストに含まれるノードをスタックオブジェクトとしてみなすことです。
連結リスト全体をスタックオブジェクトとしてみなすわけではないことに注意してください。
これにより、フルバックアップをとらずにスタックを永続化させることができます。
イメージとしては以下の図のようになります(a_0, a_1, a_2, a_3, b_2, b_3は各バージョンのスタックオブジェクトです)。
このように管理すると、各操作を以下のように実現できます。
push(x): dataがx, prevが現バージョンのスタックであるノードを連結リストに追加し、追加したノードを返す
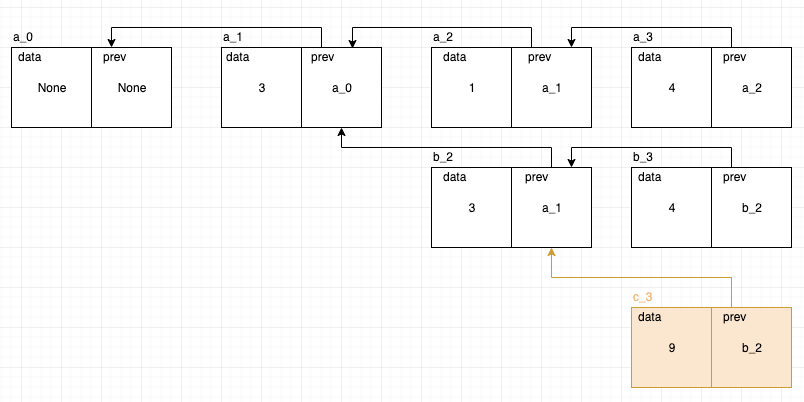
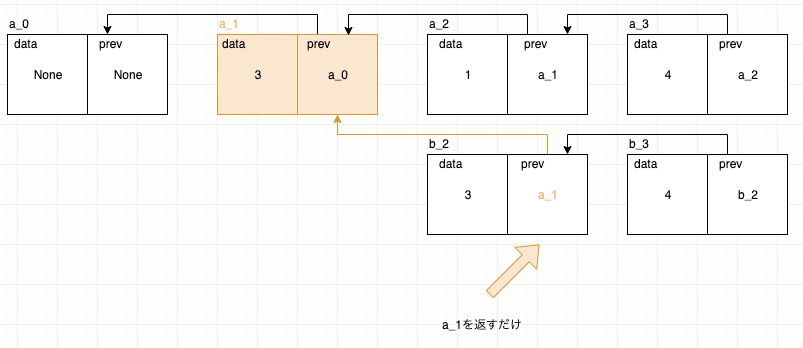
例: b_2のスタックに対してpush(9)が実行されたら、以下のc_3を作成し、作成したc_3を返せばよいです。
top(): 現バージョンのノードのdataを返す
例: b_2のスタックに対してtop()が実行されたらb_2のdataに格納されている3を返すだけです。
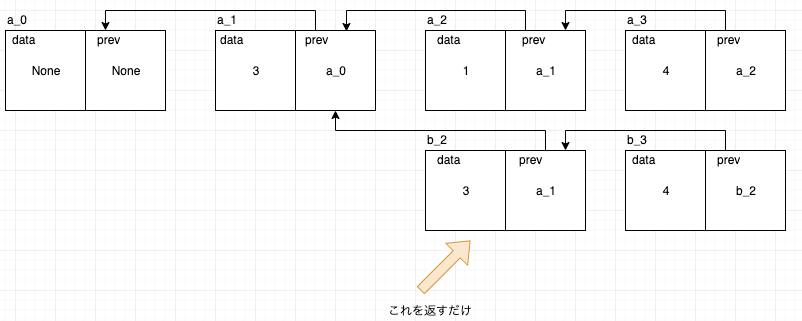
pop(): 現バージョンのノードのprevを返す
例: b_2のスタックに対してpop()が実行されたらb_2のprevがポイントしているスタックa_1を返すだけです。
各操作の処理時間はスタックサイズに依存しない、すなわち 定数時間 であることがポイントです。
永続スタックの実装
それでは永続スタックをPythonで実装してみましょう。
永続スタックを PersistentStack クラスとして実装します。
PersistentStack の prev フィールドの型を PersistentStack とする(再帰的なデータ構造にする)ことで連結リストを表現できます。
class PersistentStack:
def __init__(self, value=None, prev=None):
self.value = value
self.prev = prev
def top(self):
return self.value
def push(self, x):
return PersistentStack(x, self)
def pop(self):
return self.prev
自作した永続スタックで遊んでみましょう。
a_0 = PersistentStack()
a_1 = a_0.push(3)
print(f'a_1: {a_1.top()}')
a_2 = a_1.push(1)
print('==== a_2 まで作成 ====')
print(f'a_1: {a_1.top()}')
print(f'a_2: {a_2.top()}')
a_3 = a_2.push(4)
print('==== a_3 まで作成 ====')
print(f'a_1: {a_1.top()}')
print(f'a_2: {a_2.top()}')
print(f'a_3: {a_3.top()}')
b_2 = a_1.push(3)
b_3 = b_2.push(4)
print('==== b_3 まで作成 ====')
print(f'a_1: {a_1.top()}')
print(f'a_2: {a_2.top()}')
print(f'a_3: {a_3.top()}')
print(f'b_2: {b_2.top()}')
print(f'b_3: {b_3.top()}')
c_2 = a_1.pop()
print('==== c_2 まで作成 ====')
print(f'a_1: {a_1.top()}')
print(f'a_2: {a_2.top()}')
print(f'a_3: {a_3.top()}')
print(f'b_2: {b_2.top()}')
print(f'b_3: {b_3.top()}')
print(f'c_2: {c_2.top()}')
実行結果は下記の通りです。
a_1: 3
==== a_2 まで作成 ====
a_1: 3
a_2: 1
==== a_3 まで作成 ====
a_1: 3
a_2: 1
a_3: 4
==== b_3 まで作成 ====
a_1: 3
a_2: 1
a_3: 4
b_2: 3
b_3: 4
==== c_2 まで作成 ====
a_1: 3
a_2: 1
a_3: 4
b_2: 3
b_3: 4
c_2: None
push メソッドと pop メソッドを呼び出しても元のスタックの状態は変化していないことが分かります。
永続配列
本記事のメインコンテンツである永続配列について説明します。
永続配列の仕様
簡単のため、参照操作と更新操作のみ提供する配列を扱います。
- get(key): 配列のkey番目の要素を返す
- update(key, value): 配列のkey番目の要素をvalueに更新した後の配列を返す(この配列は変化なし)
updateは非破壊的な操作であることに注意してください。
永続配列の実装方針
木を用いて各バージョンの差分データを効率的に管理します。今回は二分木を用いることにします。
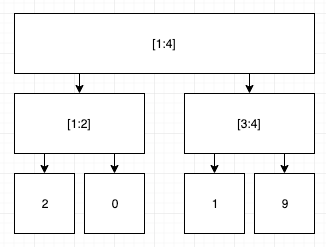
木の根は配列全体を表す頂点です。根の左の子は配列の左半分を表す頂点です。根の右の子は配列の右半分を表す頂点です。
同様に再帰的に頂点は定義されます。木の葉は配列の1要素に対応します。
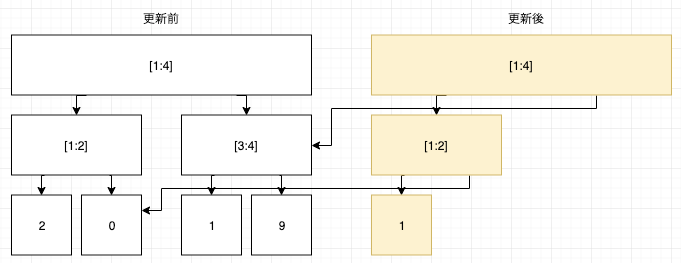
例えば、配列 $A = [2, 0, 1, 9]$ に対応する二分木は以下です。
このように配列を木に対応付けるのは一見無駄があるように思えますが、参照操作と更新操作を同時に(それなりに)高速化するための鍵となっています。
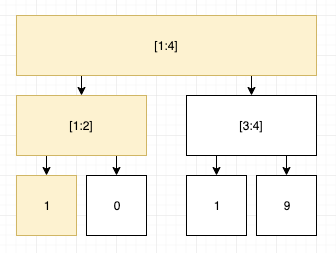
ポイントは一つの更新操作が木に与える影響は小さいということです。先ほどの例で先頭要素を1に更新する場合を考えましょう。
更新の影響を受ける頂点は以下の黄色で塗られた頂点だけです。
これは木の高さ分の個数の頂点のみ更新の影響を受けることを意味しています。
白い頂点は更新前と変わらない頂点なので以下のようにデータの管理をサボることが可能です。
これを利用して参照操作と更新操作を以下のように実装します。
- get(key): 現バージョンの木の根からスタート。key番目の要素に対応する葉に向かって下る
- update(key, value): 新しい木の根を作る。片方の子は前のバージョンの木の頂点を使い回せる。もう片方の子は新しく作る。これを再帰的に繰り返す
各操作の処理時間は木の高さに比例する時間(配列の長さについて対数時間)であることがポイントです。
永続配列の実装
各頂点をNodeクラスとして定義します。
各Nodeには以下の5個のデータを持たせます。
- start: その頂点が管理する右半開区間の始端
- stop: その頂点が管理する区間の終端
- left_child: その頂点の左の子。葉の場合はNone
- right_child: その頂点の右の子。葉の場合はNone
- value: その葉に対応する配列の要素の値。葉でない場合はNone
startとstopを持たせているのはget(key)をシンプルに処理できるようにするためです。
keyが区間[start, stop)の前半部分に属するならば左の子へ、後半部分に属するならば右の子に下るだけになります。
class Node:
def __init__(self, start, stop, left_child, right_child, value):
self.start = start
self.stop = stop
self.left_child = left_child
self.right_child = right_child
self.value = value
次に、各要素が0である配列に対応する二分木を構築する関数を定義します。簡単のため、配列の長さは2のべき乗であることを仮定します(構築される二分木は完全二分木になります)。
二分木を構築する関数は再帰的に定義できます。create_tree(start, stop)を右半開区間[start, stop)に対応する頂点とその子孫を作成する関数とします。create_tree(start, stop)を以下のように処理させればよいです。
- 区間の長さが1ならば(つまり、葉に対応する頂点ならば)、子を持たないNodeを返します(valueには0を割り当てます)。
- 区間の長さが2以上ならば(つまり、葉でない頂点ならば)、左の子と右の子を再帰的に作成し、それらを左右の子とするNodeを返します。より詳細には下記を処理します。
- create_tree(start, (start + stop) / 2) を呼び出し、作成されたNodeをLとします。ここで、[start, start + stop) / 2)は左半分の区間に対応します。
- create_tree((start + stop) / 2, stop) を呼び出し、作成されたNodeをRとします。ここで、[(strat + stop) / 2, stop)は右半分の区間に対応します。
- 新しいNodeを作成し、左の子をL, 右の子をRとします。
上記の処理をPythonのコードとして表すと下記のようになります。
def create_tree(start, stop):
is_leaf = start == stop - 1
return Node(
start=start,
stop=stop,
left_child=(None if is_leaf else create_tree(
start, (start + stop) // 2)),
right_child=(None if is_leaf else create_tree(
(start + stop) // 2, stop)),
value=(0 if is_leaf else None))
これで永続配列を作る準備ができました。永続配列をPersistentArrayクラスとして定義します。
根のデータだけ保持しておけばその二分木の各子孫に到達可能なのでPersistentArrayには根のデータのみ持たせます。
class PersistentArray:
def __init__(self, root: Node):
self.root = root
次にget(key)を実装します。前述の通り、以下の方針で実装します。
- get(key): 現バージョンの木の根からスタート。key番目の要素に対応する葉に向かって下る
今回は再帰関数findを導入して実装します。findは今いるNodeを引数とし、引数のNodeが葉ならば葉が持つ値を、そうでなければ左右の子のうち、keyが属す区間に対応する子にfindさせた結果を返すことにします。すると、get(key)はfindに根を渡した結果を返すだけでよくなります。
def get(self, key):
def find(node):
return (
node.value if node.value is not None else
find(node.left_child) if key < (node.start + node.stop) // 2 else
find(node.right_child)
)
return find(self.root)
次にupdate(key, value)を実装します。updateの実装方針は下記でした。
- update(key, value): 新しい木の根を作る。片方の子は前のバージョンの木の頂点を使い回せる。もう片方の子は新しく作る。これを再帰的に繰り返す
updateも再帰関数を導入して実装します。今回はupdate_treeという名前の再帰関数を導入します。
update_treeは(更新前 のバージョンの)今いるNodeを引数とし、引数のNodeが葉ならばvalueを持つ葉を、そうでなければ以下を処理した結果を返すことにします。
- 新しいNodeを作成します。
- 引数のNodeの左右の子のうち、keyが属さない(更新の影響を受けない)区間に対応する子を新しいNodeの子とします(更新前のバージョンのNodeを使いまわします)。
- もう片方の子をupdate_treeに渡し、その結果を新しいNodeの子とします。
すると、update(key, value)はupdate_treeに根を渡した結果を返すだけでよくなります。
def update(self, key, value):
def update_tree(node):
is_leaf = node.start == node.stop - 1
is_in_left = key < (node.start + node.stop) // 2
return Node(
start=node.start,
stop=node.stop,
left_child=(
None if is_leaf else
update_tree(node.left_child) if is_in_left else
node.left_child
),
right_child=(
None if is_leaf else
node.right_child if is_in_left else
update_tree(node.right_child)
),
value=(value if is_leaf else None)
)
return PersistentArray(update_tree(self.root))
これで永続配列は完成しました!
最後に、初期化がちょっと面倒なので各要素の初期値が0であるような永続配列を生成する関数を作ります。
def new_persistent_array(n):
return PersistentArray(create_tree(0, n))
永続配列に関するコードをまとめます。
class Node:
def __init__(self, start, stop, left_child, right_child, value):
self.start = start
self.stop = stop
self.left_child = left_child
self.right_child = right_child
self.value = value
def create_tree(start, stop):
is_leaf = start == stop - 1
return Node(
start=start,
stop=stop,
left_child=(None if is_leaf else create_tree(
start, (start + stop) // 2)),
right_child=(None if is_leaf else create_tree(
(start + stop) // 2, stop)),
value=(0 if is_leaf else None))
class PersistentArray:
def __init__(self, root):
self.root = root
def get(self, key):
def find(node):
return (
node.value if node.value is not None else
find(node.left_child) if key < (node.start + node.stop) // 2 else
find(node.right_child)
)
return find(self.root)
def update(self, key, value):
def update_tree(node):
is_leaf = node.start == node.stop - 1
is_in_left = key < (node.start + node.stop) // 2
return Node(
start=node.start,
stop=node.stop,
left_child=(
None if is_leaf else
update_tree(node.left_child) if is_in_left else
node.left_child
),
right_child=(
None if is_leaf else
node.right_child if is_in_left else
update_tree(node.right_child)
),
value=(value if is_leaf else None)
)
return PersistentArray(update_tree(self.root))
def new_persistent_array(n):
return PersistentArray(create_tree(0, n))
使用例
N = 8
A = new_persistent_array(N)
print([A.get(i) for i in range(N)])
B = A.update(0, 3)
C = B.update(2, 1)
print('==== Aを更新 ====')
print([A.get(i) for i in range(N)])
print([B.get(i) for i in range(N)])
print([C.get(i) for i in range(N)])
出力
[0, 0, 0, 0, 0, 0, 0, 0]
==== Aを更新 ====
[0, 0, 0, 0, 0, 0, 0, 0]
[3, 0, 0, 0, 0, 0, 0, 0]
[3, 0, 1, 0, 0, 0, 0, 0]
updateを呼び出した後も更新前の配列には影響を与えていないことが分かります。
永続配列を用いた効率的なオンラインアルゴリズム
永続配列を用いて配列のバージョン管理問題を解くオンラインアルゴリズムを考えてみましょう。とは言っても、とくに工夫は不要です。
各更新操作に対して、更新後の永続配列オブジェクトを保持しておき、それを用いてクエリ回答するだけです。
Pythonでの実装例は以下です。
# 配列の初期状態
A = [2, 0, 1, 9]
# 更新操作
operations = [('a.0', 2, 2, 'a.1'), ('a.1', 0, 1, 'a.2'), ('a.2', 1, 1, 'a.3'),
('a.1', 3, 0, 'b.2'), ('a.3', 3, 3, 'a.4')]
# 初期状態の永続配列を作成
A_init = new_persistent_array(N)
for i, a in enumerate(A):
A_init = A_init.update(i, a)
cache = {'a.0': A_init}
# 永続配列により各更新操作後の配列をバージョン管理
for version, index, new_value, next_version in operations:
cache[next_version] = cache[version].update(index, new_value)
# クエリに回答する関数(クエリの先読みはしていない)
def answer(version, index):
print(f'{version}: A[{index}] = {cache[version].get(index)}')
# クエリ
queries = [('a.1', 2), ('a.4', 1), ('a.4', 3), ('b.2', 3)]
# 各クエリに対してフルバックアップを用いて回答する
for version, index in queries:
answer(version, index)
永続配列を用いている点を除けば、フルバックアップによるオンラインアルゴリズムとほとんど同じ実装です。
永続配列の更新操作と参照操作は対数時間で実行できるため、各更新操作、および、クエリ回答も対数時間で実行できます。
さすがに計算量の効率ではオフラインアルゴリズムには敵わないですが、シンプルな実装でオンラインアルゴリズムをオーダーレベルで改善できることから永続データ構造の強力さが伺えると思います。
実験
本記事では配列のバージョン管理問題を解く方法として、以下の4つを紹介しました。
- オフラインアルゴリズム
- フルバックアップ
- 状態復元
- 永続配列
それぞれの方法について、少し規模が大きい問題に対する実行時間を測定し比較してみましょう。
実験ケース
まず、テストデータを以下のルールにしたがってランダムに生成します。
- 配列の各要素の初期値は0以上1000以下の整数から一様ランダムに選ばれる
- 更新操作について
- 更新操作の数全体の10%, 20%, 30%, ..., 90%の更新操作が完了したタイミングでバージョンの枝分かれは発生する(最終的な枝の本数は10本になる)
- 更新対象バージョンはその時点で存在する枝から一様ランダムに選んだ枝の先端のバージョンとする
- 更新対象インデックスは一様ランダムに選ばれる
- 更新後の値は0以上1000以下の整数から一様ランダムに選ばれる
- クエリについて
- 各クエリの対象バージョンは全バージョンから一様ランダムに選ばれる
- 対象インデックスは一様ランダムに選ばれる
更新操作のルールについて補足します。
枝分かれが多すぎると(例えば、その時点で存在する全バージョンから一様ランダムに選んだものを更新対象バージョンとすると)、バージョンツリーの深さが短すぎて状態復元による方法が非常に有利になってしまいます。
今回はそれなりに悪いケースにおける計算量を比較したいので、上記のルールのように枝分かれの数を抑えています。
また、配列のバージョン管理を現実的なアプリケーションに応用することを考えた場合、(当然アプリケーションの性質にもよりますが)枝分かれが乱立するケースは考えにくいと思います。
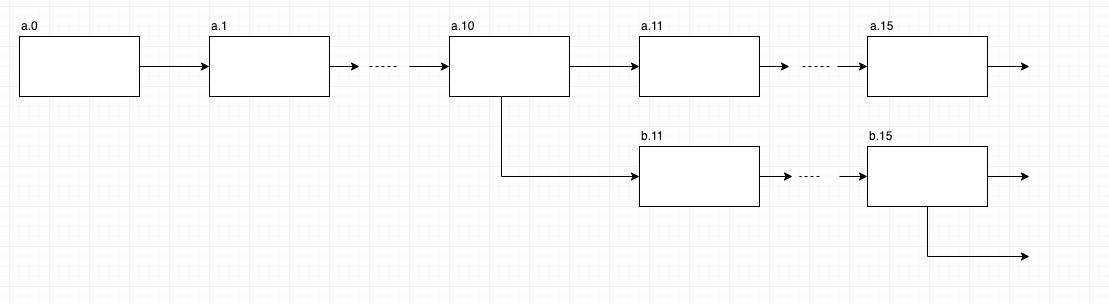
更新操作数が100のときのバージョンツリーのイメージ図は以下です。
実験ケースとして以下の4つを扱います。
- 小規模
- 配列の長さ: 1万
- 更新操作数: 1万
- クエリ数: 1万
- 配列が長い
- 配列の長さ: 5万
- 更新操作数: 1万
- クエリ数: 1万
- 更新操作数が多い
- 配列の長さ: 1万
- 更新操作数: 5万
- クエリ数: 1万
- クエリ数が多い
- 配列の長さ: 1万
- 更新操作数: 1万
- クエリ数: 5万
実験結果
各方法・各ケースに対する実行時間(単位: 秒)の比較表は以下の通りです(ついでに最悪計算量オーダも掲載しています; $N$ は配列の長さ、 $M$ は更新操作数、 $Q$ はクエリ数です)。
| 方法 | 最悪計算量オーダ | 小規模 | 配列が長い | 更新操作数が多い | クエリ数が多い |
|---|---|---|---|---|---|
| オフラインアルゴリズム | $O(N + M + Q)$ | 0.52 | 0.53 | 0.67 | 0.59 |
| フルバックアップ | $O(NM + Q)$ | 10.24 | 47.25 | 61.63 | 10.03 |
| 状態復元 | $O(N + MQ)$ | 8.25 | 7.95 | 39.50 | 35.56 |
| 永続配列 | $O(M \log{N} + Q\log{N})$ | 1.46 | 3.05 | 4.47 | 1.79 |
やはりオフラインアルゴリズムはダントツで高速ですね。クエリを先読みできるケースのアドバンテージが伺えます。バッチ処理が可能であるならばその恩恵を最大限に利用すべきでしょう。
オンラインアルゴリズムについて、永続配列は各ケースにおいて優れた計算速度となっています。本問題に対して特殊な仮定がなければ永続配列を用いれば間違いないでしょう。フルバックアップはクエリ数の増加に強く、状態復元は配列の長さの増加に強いことが分かります。これらの数に大きな偏りがあるならばフルバックアップまたは状態復元による方法の採用を検討すべきでしょう。
永続データ構造ライブラリの紹介
ここまで永続データ構造を手作りしてきましたが、多くの言語ではライブラリとして既に提供されています。
手作りも楽しいですが、実用においてはライブラリの活用も検討すべきでしょう。
ここではPythonとJavaScriptの永続データ構造ライブラリを紹介します。
Pyrsistent(Python)
GitHubリポジトリ: https://github.com/tobgu/pyrsistent
Pyrsistentが提供する永続データ構造と標準ライブラリのデータ構造との対応関係は以下の通りです。
| 提供する永続データ構造 | 対応するデータ構造 |
|---|---|
| PVector | list |
| PSet | set/frozenset |
| PMap | dict |
| PDeque | deque |
PはPersistent(永続的)の頭文字をとっていると思われます。
Pyrsistentはpipでインストールできます。
pip install pyrsistent
Pyrsistentを用いて冒頭の問題を解くコードは以下のようになります。
from pyrsistent import v
# 配列の初期状態
A = [2, 0, 1, 9]
# 更新操作
operations = [('a.0', 2, 2, 'a.1'), ('a.1', 0, 1, 'a.2'), ('a.2', 1, 1, 'a.3'),
('a.1', 3, 0, 'b.2'), ('a.3', 3, 3, 'a.4')]
cache = {'a.0': v(A)}
# 永続配列により各更新操作後の配列をバージョン管理
for version, index, new_value, next_version in operations:
cache[next_version] = cache[version].set(index, new_value)
# クエリに回答する関数(クエリの先読みはしていない)
def answer(version, index):
print(f'{version}: A[{index}] = {cache[version][index]}')
# クエリ
queries = [('a.1', 2), ('a.4', 1), ('a.4', 3), ('b.2', 3)]
# 各クエリに対してフルバックアップを用いて回答する
for version, index in queries:
answer(version, index)
immutable-js(JavaScript)
GitHubリポジトリ: https://github.com/immutable-js/immutable-js
immutable-jsが提供する永続データ構造と標準ライブラリのデータ構造との対応関係は以下の通りです。
| 提供する永続データ構造 | 対応するデータ構造 |
|---|---|
| List | Array |
| Set | Set |
| Map | Map |
immutable-jsはnpmでインストールできます。
npm i immutable
immutable-jsを用いて冒頭の問題を解くコードは以下のようになります。
const { List } = require('immutable');
// 配列の初期状態
A = [2, 0, 1, 9]
// 更新操作
operations = [
['a.0', 2, 2, 'a.1'], ['a.1', 0, 1, 'a.2'], ['a.2', 1, 1, 'a.3'],
['a.1', 3, 0, 'b.2'], ['a.3', 3, 3, 'a.4']
]
cache = { 'a.0': List(A) }
// 永続配列により各更新操作後の配列をバージョン管理
operations.forEach(([version, index, new_value, next_version]) => {
cache[next_version] = cache[version].set(index, new_value)
})
// クエリに回答する関数(クエリの先読みはしていない)
function answer(version, index) {
console.log(`${version}: A[${index}] = ${cache[version].get(index)}`)
}
// クエリ
queries = [['a.1', 2], ['a.4', 1], ['a.4', 3], ['b.2', 3]]
// 各クエリに対してフルバックアップを用いて回答する
queries.forEach(([version, index]) => answer(version, index))
おわりに
- 永続データ構造を用いると非破壊的な更新操作と参照操作を効率的に処理できます
- 永続データ構造は連結リストや木を用いることで操作処理時間を効率化しています
- 多くの言語のサードパーティ・ライブラリで永続データ構造が提供されています
ぜひ永続データ構造を使ってみてください!
参考記事
-
あなたの庭に永続データ構造を飾りませんか?
- 永続データ構造の概要と永続スタックの実装について参考にしました
-
永続データ構造【新歓ブログリレー2019 6日目】
- 永続配列の実装について参考にしました