問題がNP完全であることを証明するには

FUJITSU Advent Calendar 2018 18日目の記事です。

はじめに

ある問題がNP完全であることを証明する方法について、一般的な方法と具体例を紹介します。

NP完全とは

クラスNPに属す問題であり、かつ、クラスNPに属す任意の問題と同等以上に難しい問題を NP完全 といいます。
ざっくり言うと、Yes/Noで回答する問題であり、かつ、正解を計算するのがとても難しいと信じられている問題です。
問題のクラスについて、 P、NP、NP完全、NP困難…似て非なる階層構造 で詳しく説明されています。
また、NP困難 --- Wikipedia のベン図は各クラスの関係性を理解する助けになるかと思います。

問題がNP完全であることを証明すると何が嬉しいのか

アルゴリズム設計対象の問題がNP完全であることが証明されると、アルゴリズム設計者は以下の妥協に踏み切れます¹。

• 近似アルゴリズムを採用する
• 特殊なケースに対してのみ適用可能なアルゴリズムに制限する

なぜならば、NP完全問題に対して、多項式時間で解けるアルゴリズムを設計できる望みは絶望的だと信じられているからです。

問題がNP完全であることを証明するには

ある問題がNP完全であることを証明するには、以下の2つを示せばよいです。

• その問題がクラスNPに属すこと
• 既知のNP完全問題からその問題に多項式時間帰着可能であること

問題がクラスNPに属すこと

その問題の解がYesのとき、Yesとなる証拠が与えられれば、解が本当にYesであることを多項式時間で確認できる問題です。
ざっくり言うと、Yesであることの答え合わせは簡単な問題と言ったところでしょうか。

既知のNP完全問題からその問題に多項式時間帰着可能であること

こちらが証明のメインパートになります。

まず、これまでに数多くのNP完全問題が発見されています。
An Annotated List of Selected NP-complete Problems

これらのNP完全問題からその新しい問題に多項式時間帰着可能であるかを示せばよいです。
多項式時間帰着とは、以下を満たす問題の変換です。

• 問題のサイズに関して多項式時間で、帰着前の問題から帰着後の問題を得られる
• 帰着前の問題の解がYesならば帰着後の問題の解もYesである
• 帰着後の問題の解がYesならば帰着前の問題の解もYesである

気持ちとしては、帰着前の問題は非常に難しいと信じられているのにも関わらず、大した時間を要さない変換により、帰着後の問題が簡単に解けるとは信じがたい。
したがって、帰着後の問題も非常に難しいと信じられる、と言ったところでしょうか。

例題: タスク交換問題

本記事のメインです。
タスク交換問題という現実にもありそうな具体的な問題について、それがNP完全であることを証明してみましょう。

問題の定義

AliceとBobがいます。以下の状況を考えます。

• Aliceにいくつかのタスクが割り当てられています
• Bobにもいくつかのタスクが割り当てられています
• 各タスク（Bobに割り当てられたタスクも含む）について、Aliceが着手した場合の所要時間は見積もられています
• 各タスク（Aliceに割り当てられたタスクも含む）について、Bobが着手した場合の所要時間は見積もられています

このとき、AliceおよびBobにとって、「交換後に自身に割り当てられたタスクの所要時間の和」が
「交換前に自身に割り当てられたタスクの所要時間の和」より小さくなるようなタスク交換（以降、 Win-Win交換 と呼びます）は存在するでしょうか。
ここで、タスク交換は $1:1$ に限らず、 $n:m$ でもよいとします。

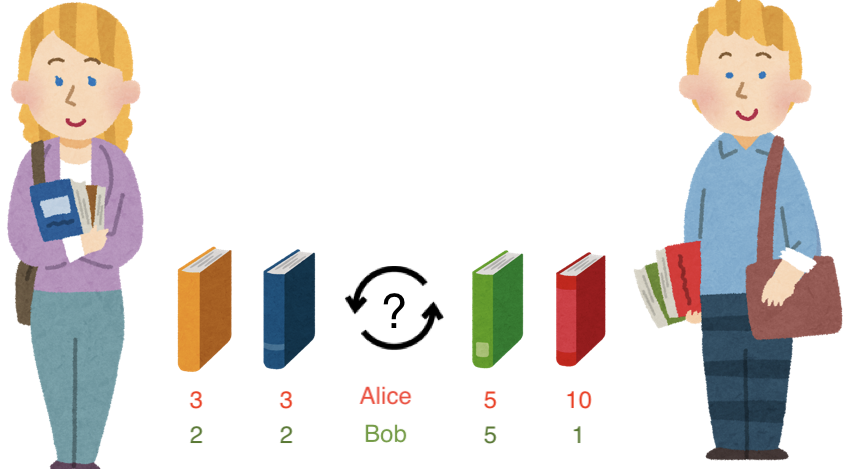
問題の例: 解がYes

• AliceにタスクA, Bが割り当てられています
• BobにタスクC, Dが割り当てられています
• 各タスクについて、AliceおよびBobが着手した場合の所要時間は以下です

タスク	Alice	Bob
A	3	2
B	3	2
C	5	5
D	10	1

このとき、Aliceに割り当てられているタスクA, BとBobに割り当てられているタスクCの交換はWin-Win交換となります。
なぜならば、そのような交換をすると、

• Aliceの所要時間の和は $6$ から $5$ になります
• Bobの所要時間の和は $6$ から $5$ になります

問題の例: 解がNo

• AliceにタスクA, Bが割り当てられています
• BobにタスクC, Dが割り当てられています
• 各タスクについて、AliceとBobが着手した場合の所要時間は以下です

タスク	Alice	Bob
A	3	4
B	3	2
C	5	5
D	10	1

このとき、いかなるタスク交換に関しても、Win-Win交換ではありません。

タスク交換問題がNP完全であることを証明する

クラスNPに属すことの証明

与えられたタスク交換について、交換後のAliceとBobの所要時間の和は多項式時間で計算できます。
当然、交換前のAliceとBobの所要時間の和も多項式時間で計算できます。
それらの大小関係の比較も多項式時間で計算できます。
以上より、タスク交換問題の解がYesならば、証拠となるタスク交換が与えられたとき、解が本当にYesであることを多項式時間で確認できます。

分割問題からタスク交換問題に多項式時間で帰着させる

分割問題は、NP完全であることが既に証明されている問題です。
分割問題をざっくり説明します。
$n$ 個の自然数のリスト $a=[a_1, a_2, \ldots, a_n]$ が与えられます。
このとき、和が等しくなるようにリスト $a$ を二分割できるかを問う問題です（分割は連続する要素でなくともよいです）。
例えば、リスト $a=[1, 2, 3, 4, 6]$ が与えられたとき、 $[1, 3, 4]$ と $[2, 6]$ で二分割すると、それぞれ和が $8$ になるので解はYesです。
例えば、リスト $a=[1, 2, 3, 5, 6]$ が与えられたとき、 $a$ をどう二分割しても和は等しくならないので解はNoです。
少し考えると、リスト $a$ の和を $S$ とするとき、和が $S/2$ となるようなサブリストの存在を問う問題であることが分かります。
また、 $S$ が奇数ならば解がNoであることは明らかです。
以降、議論を簡単にするため、 $S$ が偶数である分割問題のみ考えます。

さて、分割問題からタスク交換問題への以下の帰着を考えます（ $\varepsilon$ は $0 < n \varepsilon < 1$ を満たす実数、例えば$\varepsilon = 1/(n +1)$ とします）。

• Aliceに $n$ 個のタスク $T_1, T_2, \ldots, T_n$ が割り当てられています
  • $n$ は分割問題のリストのサイズです
  • 分割問題のリストの各要素をAliceのタスクに対応付けています
• Bobに $1$ 個のタスク $T'$ が割り当てられています
  • 帰着元である分割問題に依存せず、常に $1$ 個のタスクです
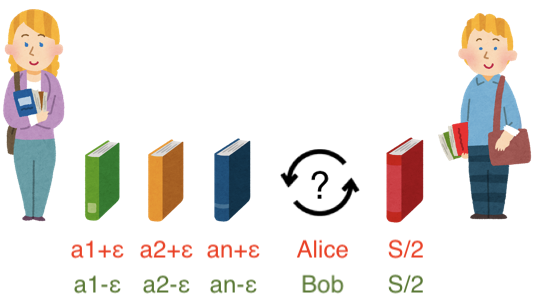
• 各タスクについて、AliceとBobが着手した場合の所要時間は以下です（$S$ はリスト $a$ の和です）

タスク	Alice	Bob
$T_1$	$a_1 + \varepsilon$	$a_1 - \varepsilon$
$T_2$	$a_2 + \varepsilon$	$a_2 - \varepsilon$
...	...	...
$T_n$	$a_n + \varepsilon$	$a_n - \varepsilon$
$T'$	$S/2$	$S/2$

この帰着は $n$ に比例する時間で実行可能です。
すなわち、この帰着は多項式時間で実行可能です。

注目すべき点として、帰着後の問題は、Bobにはタスクが1個しか割り当てられていません。
このような極端な問題であっても、タスク交換問題は既知のNP完全問題と同程度に難しいのです（まだ証明できていませんが）。
今回のように、あえて極端なケースにフォーカスし、既知のNP完全問題と見比べると帰着が閃くこともよくあります。

話が脱線しました。
あとは帰着前の分割問題と帰着後のタスク交換問題の解が一致することを示すだけです。

分割問題の解がYesならばタスク交換問題の解もYesであることの証明

帰着元の分割問題は、 リスト $a$ をリスト $a'$　と リスト $a''$ に分割することにより、それらの和を等しくできるものとします。
このとき、 帰着後のタスク交換問題について、 リスト $a'$ に対応するAliceのタスクとBobのタスクの交換はWin-Win交換であることが言えます。
なぜならば、 リスト $a'$ のサイズを $n'$, リスト $a''$ のサイズを $n''$ として、以下が成り立つからです。

• 交換前のAliceの所要時間: （$a$ に対応するタスクの所要時間の和） = $a_1 + a_2 + \cdots + a_n + n \varepsilon = S + n \varepsilon$
• 交換後のAliceの所要時間: （$a''$ に対応するタスクの所要時間の和） + （$T'$ の所要時間） = $S/2 + n'' \varepsilon + S/2 = S + n'' \varepsilon$
• 交換前のBobの所要時間: （$T'$ の所要時間） = $S / 2$
• 交換後のBobの所要時間: （$a'$ に対応するタスクの所要時間の和） = $S/2 - n' \varepsilon$

$n'' \varepsilon < n \varepsilon$ より、Aliceにとって、交換後のタスクのほうが所要時間は小さいです。
$n' \varepsilon > 0$ より、Bobにとっても、交換後のタスクのほうが所要時間は小さいです。

以上より、リスト $a'$ に対応するAliceのタスクとBobのタスクの交換はWin-Win交換です。

タスク交換問題の解がYesならば分割問題の解もYesであることの証明

帰着後のタスク交換問題は、Aliceのタスクのリストの一部 $\mathcal{T}$ と Bobのタスク $T'$ の交換をWin-Win交換として解を持つとします。
このとき、 帰着前の分割問題について、 リスト $a$ を Alice が交換に出すタスクのリスト $\mathcal{T}$ に対応するリスト $a'$ と
対応しないリスト $a''$ に分割することにより、それらの和が等しくなることが言えます。
以降、その理由を述べます。

まず、交換前後のAliceとBobの所要時間は以下です。

• 交換前のAliceの所要時間: （$a$ に対応するタスクの所要時間の和） = $a_1 + a_2 + \cdots + a_n + n \varepsilon = S + n \varepsilon$
• 交換後のAliceの所要時間: （$a''$ に対応するタスクの所要時間の和） + （$T'$ の所要時間） = （$a''$ の和） + $n'' \varepsilon + S/2$
• 交換前のBobの所要時間: （$T'$ の所要時間） = $S / 2$
• 交換後のBobの所要時間: （$a'$ に対応するタスクの所要時間の和） = （$a'$ の和）- $n' \varepsilon$

交換後のAliceの所要時間は交換前のAliceの所要時間より小さいので、
（$a''$ の和） + $n'' \varepsilon + S/2 < S + n \varepsilon$
が成り立ちます。
したがって、
（$a''$ の和） < $S/2 + (n - n'') \varepsilon$
が成り立つます。
さらに、 $S/2 + (n - n'') \varepsilon < S/2 + n \varepsilon < S/2 + 1$ より、
（$a''$ の和） < $S/2 + 1$
が成り立ちます。

次に、交換後のBobの所要時間は交換前のBobの所要時間より小さいので、
（$a'$ の和） - $n' \varepsilon < S/2$
が成り立ちます。
したがって、
（$a'$ の和） < $S/2 + n' \varepsilon$
が成り立ちます。
さらに、（$a'$ の和） + （$a''$ の和） = $S$ より、
（$a'$ の和） = $S$ - （$a''$ の和）が成り立つので、
$S$ - （$a''$ の和） < $S/2 + n' \varepsilon$
が成り立ちます。
これを変形すると、
（$a''$ の和） > $S/2 - n' \varepsilon$
を得ます。
さらに、 $S/2 - n' \varepsilon > S/2 - n \varepsilon > S/2 - 1$ より、
（$a''$ の和） > $S/2 - 1$
を得ます。

赤字の不等式をまとめます。
$S/2 - 1$ < （$a''$ の和） < $S/2 + 1$
今回、 $S$ は偶数と仮定しているので、 $S/2$ は整数です。
したがって、
（$a''$ の和） = $S/2$
が成り立ちます。
（$a'$ の和） + （$a''$ の和） = $S$ より、
（$a'$ の和） = $S/2$
も成り立ちます。

以上より、リスト $a'$ の和とリスト $a''$ の和は等しいです。

証明のまとめ

これまでの議論により、

• タスク交換問題はクラスNPに属すこと
• 分割問題からタスク交換問題への多項式時間帰着が存在すること

が示されたので、タスク交換問題はNP完全であることが証明されました。

おわりに

• NP完全問題とは、ざっくり言うと、Yes/Noで回答する問題であり、かつ、正解を計算するのがとても難しいと信じられている問題です
• アルゴリズム設計対象の問題がNP完全であることを証明すると、アルゴリズム設計者は妥協に踏み切れるというメリットがあります
• NP完全であることを証明するには、クラスNPに属すこと、および、既知のNP完全問題から多項式時間帰着可能であることを示せばよいです
• タスク交換問題のような身近な問題にもNP完全問題はあります

1. アルゴリズムイントロダクション を参考にしました。 ↩