Pythonでマージソート実装・計算量の解析と実験

今回はソートアルゴリズムのマージソート(分割統治法を使用)についてです。
ソートアルゴリズムとはデータ構造内での要素を昇順や降順などのように並べ替えたりするアルゴリズムで、マージソートはその中で最もよく目にするアルゴリズムのひとつです。

#アルゴリズムの解説
マージソートでは基本的に配列を使って並び替えを行っていきますが、その名のとおり配列を分割してから混合します。この混合をしている間に各要素を比較して並べ替えていきます。結果、並べ替えされた配列が手に入ります。
#####分割
まず分割を行う際には配列の真ん中の値をmid = (low+high)/2で求めます。例えば配列の長さがnの時はmid = (0+(n-1))/2が真ん中の値で0からmidまでとmid+1からn-1までの配列二つに分割し、それらを繰り返し分割していき配列の長さが１になれば分割を終了します。分割では各々の配列が二つの配列に分かれる為、二分木構造のように１つの長い配列が親となり、二つの同じ長さの短い配列を子として持ちます。この結果、深さがベースを２とするlog(n)の木構造が作成されたと思ってください。
#####統治
統治をする時には二つの子配列の先頭の要素を比較して親のリストの先頭に入れます。次に選んだ要素が含まれたリストのアクセスするインデックスを１つインクリメントして二つ目の要素と片方の先頭の要素を比較して親のリストの次のインデックスに格納します。こうして選ばれたほうのインデックスの値をインクリメントしていき、親のリストへ格納する作業を子のリストのどちらか片方の末尾の要素まで繰り返し、要素が余ったリストの要素を順に格納します。これを木構造の末端ノードからルートノードまで順に繰り返していくと、最後のルートノードで並べ替えられた配列が出来上がっているというかんじです。

グラフでわかりやすく解説したウェブサイトを最後に貼っておきます。

#実装
簡単にマージソートの関数を実装したので説明していきます。各行の右側にコメントで行番号を１からつけておきました。

merge_sort.py

def merge(array):                                   # line1
    mid = len(array)                                # line2
    if mid > 1:                                     # line3
        left = merge(array[:(mid/2)])               # line4
        right = merge(array[(mid/2):])              # line5
        array = []                                  # line6
        while len(left) != 0 and len(right) != 0:   # line7
            if left[0] < right[0]:                  # line8
                array.append(left.pop(0))           # line9
            else:                                   # line10
                array.append(right.pop(0))          # line11
        if len(left) != 0:                          # line12
            array.extend(left)                      # line13
        elif len(right) != 0:                       # line14
            array.extend(right)                     # line15
    return array                                    # line16

・line1でパラメーターでとる値を要素に整数しか含まない配列と仮定して作りました。

・line2で配列の長さの値を求めましたが先述の説明と少し違うのはPythonで分割する度に新しい配列を作成したからです。JAVAとかのarrayの場合は不変性のオブジェクトで１つの配列のインデックス番号を計算したりしながら分割するので先述した方法で求めてください。

・line3では配列の長さが１以上より長いかを判定して長ければline4~line15までのコードを実行して、短ければそのまま配列を戻り値として返します。

・line4と5では再帰的に親のリストを半分にスライシングした配列をパラメーターに与えて関数を呼び出しています。

・ここまでのコードで解ると思いますが、再帰的に関数を呼ぶ事により配列が１になるまで分割していきます。

・line6で親の配列を空にしているのはこの後でリストに値を入れる時にメソッドのappend()(リストの末尾に要素を追加)を使用するからです。元の配列ではすでにいくつかの要素を含んでおり要素の追加では不便だと思い空にしました。

・line7ではループを用いましたがどちらか片方のリストが空でない限りループし続けます。

・line8~11で両方の配列の先頭の要素を比較してより小さい要素を含んだ配列の先頭の要素を削除し親の配列の末尾に付け加えています。この作業を片方のリストが空になるまで続けます。

・line12~15ではline7のループが終わった時に片方のリストは空になるがもう片方のリストは最低でも１つの要素を残しているので、どちらかの配列の残った要素をまとめて親のリストに付け加えます。

・line16では各々の並び替えた配列を戻り値として返し、各々の配列の親の配列に並び替えてルートノードに達すればパラメーターに与えた配列のすべての要素が並び替えられた状態で返してくれます。

#計算量
T(n)をマージソートの全体の計算量でnが配列の要素の数もしくは配列の長さとします。T(0)とT(1)は何もしないので計算量は０となります。
マージソートではまず配列を半分にして再帰的にマージソートを呼ぶのでT(n/2)が再帰的に呼んだ時の計算量(line4と5)でこれを２回行うのでT(n/2) + T(n/2) = 2T(n/2)が両方を呼んだ時(line4~5)となります。これに加えてマージソートは最悪の場合n-1回ループするので全体の計算量がT(n) = 2T(n/2) + n - 1となります。
これでマージソートの配列の長さがnの時の計算量がわかりましたが、マージソートは配列を半分にして再帰的に呼ぶのでT(n/2),T(n/4),T(n/8)・・・・・・・T(n/(2^(k-1)))の時の計算量も調べていきます。kは再帰的に呼ばれる回数でk = 1から始まります。
T(n/2) = 2T(n/4) + n/2 - 1,
T(n/4) = 2T(n/8) + n/4 - 1,
T(n/8) = 2T(n/16) + n/8 - 1,
・
・
・
・
・
T(n/2^(k-1)) = 2T(n/2^k) + n/2^(k-1) - 1
がk>=1の時の計算量となります。

これをT(n)の式に代入するとこうなります。
T(n) = 2(2T(n/4) + n/2 - 1) + n - 1 = 4T(n/4) + 2n - (1 + 2)
= 4(2T(n/8) + n/4 - 1) + 2n - (1 + 2) = 8T(n/8) + 3n - (1 + 2 + 4)
= 8(2T(n/16) + n/8 - 1) + 3n - (1 + 2 + 4) = 8T(n/8) + 4n - (1 + 2 + 4 + 8)
　　　・
　　　・
　　　・
　　　・
　　　・
= 2^kT(n/2^k) + k*n - (1 + 2 + 4 + ・・・・・ + 2^(k-1))
となります。

これで
T(n) = 0, もしn=0,1
T(n) = 2^kT(n/2^k) + (k*n - k) - (1 + 2 + 4 + ・・・・・ + 2^(k-1)),
もし2 <= n <= k だという事が解りました。

ここで再帰的呼び出しがk回行われるという事は木構造でk階層あるという事になり2^kはk階層目のnの値であるといえます。したがってn = 2^kでこれをkについて解くとk = log(n)となりこれらをT(n)の式に代入すると、
T(n) = nT(2^k/2^k) + log(n)*n - log(n) - (1 + 2 + 4 + ・・・・・ + 2^(log(n)-1))
= nT(1) + nlog(n) - log(n) - (2^log(n) - 1)
= nlog(n) - log(n) - (2^log(n) - 1)

最初の項はT(1) = 0からn*0 = 0となり、最後の項は総和の公式(Wikipediaを参照しました。)からこうなりました。
nlog(n) > 2^log(n)なので計算量オーダーはO(nlog(n))となります。ちなみにマージソートでは平均計算量も最善計算量も最悪計算量と同じになります。

#グラフ化
実際に平均時間を計算してグラフ化したのでソースコードとグラフを張っておきます。

merge_sort.py

import math
import random
import time
import matplotlib.pyplot as plt

#ここへマージソートの関数をコピペ

sumOfTime = 0
sumPltList = []
nlognList = []
list1 = []
# 配列の長さ0から3000までを作るループ
for i in range(3000):
    # 各々の長さiの配列に対し100回マージソートするループ
    for j in range(100):
        # 各インデックスに0~100000の中からランダムな数字を入れる
        for k in range(i):
            list1.append(random.randint(0,100000))
        # マージソート前の時間
        t0 = time.clock()
        merge(list1)
        # マージソート後の時間
        t1 = time.clock()
        #　次のマージソートの為に配列を空にしておく
        list1 = []
        # マージソートを行った時間の差異の総和
        sumOfTime += t1 - t0
    # 100回行ったマージソートの平均値
    sumOfTime /= 100
    # 平均時間をi個をリストへ格納、2000000は帳尻を合わせたので根拠はない
    sumPltList.append(sumOfTime*2000000)
    # log(0)の対処してilog(i)を比較対象としてi個をリストへ格納
    if i != 0:
        nlognList.append(i*math.log(i)/math.log(2))
    else:
        nlognList.append(0.0)
    # 時間の総和を100回毎にリセット
    sumOfTime = 0
# マージソートとnlog(n)の曲線を描く
plt.plot(sumPltList, "r-", label = "Merge_Sort")
plt.plot(nlognList, "g-", label = "O(nlogn)")
# レーベルを左上に表示
plt.legend(loc=2)
# x軸、y軸にレーベルをつける
plt.xlabel('number of elements in a list')
plt.ylabel('time be taken')
#グラフの表示
plt.show()

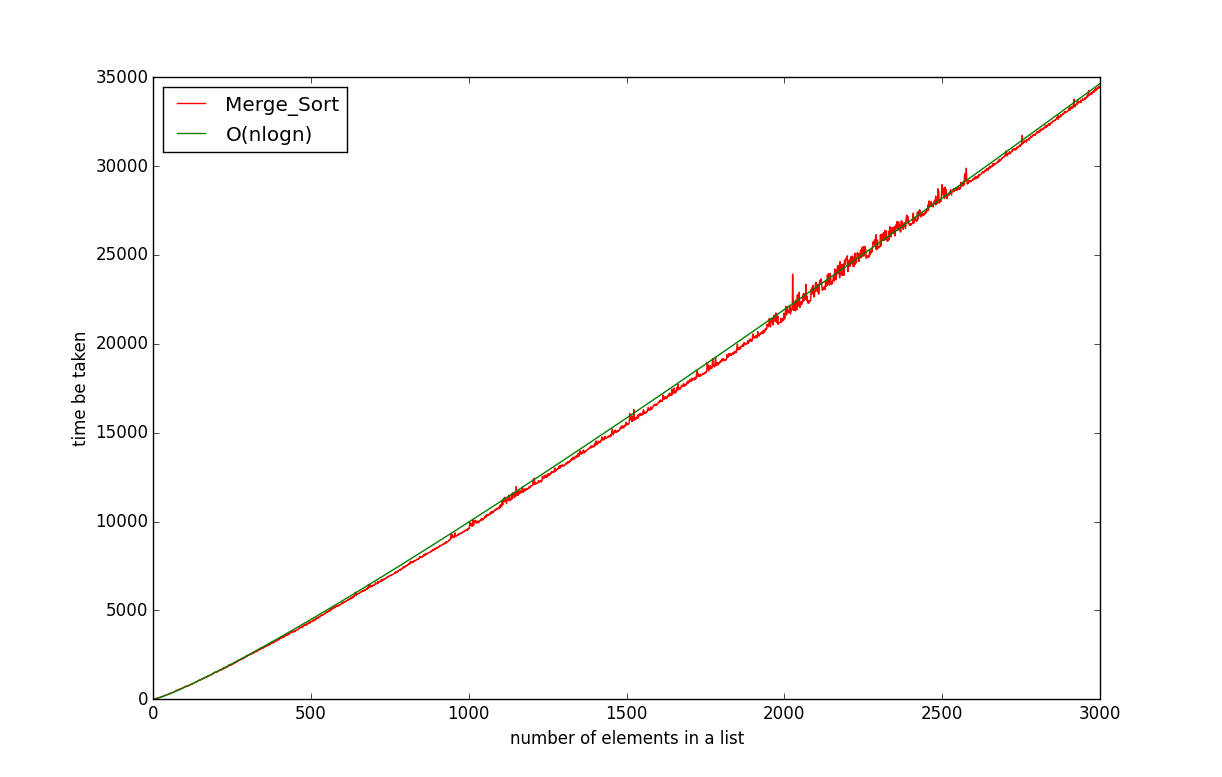
2000000を平均時間に掛けたのは長さ99の配列までの結果を見て帳尻をあわせましたが、長さ3000までの結果でどうなるかが下のグラフです。

長さ100から3000までの計算量の値もほぼnlog(n)の値と近似してることから、計算量の実験は成功と言ってよいと思います。

今回はマージソートのアルゴリズムの説明、実装、解析をしていきましたが、もし誤っている点、あやふやに感じる点などありましたらコメントもしくはメールしてください。よろしくお願いします。次回はPythonのステートメントか他のアルゴリズムをPythonで実装していくと思います。最後まで読んでいただきありがとうございました！

マージソートのリンク: http://www.ics.kagoshima-u.ac.jp/~fuchida/edu/algorithm/sort-algorithm/merge-sort.html