arxiv
IEEE
この論文では、重みの一部を削除することでニューラルネットを高速化する際に、重みのフィッシャー情報量に基づいて削除することを提案しています。これにより、性能の低下が抑えられるとされています。
フィッシャー情報量とは
フィッシャー情報量の定義はここがわかりやすいでしょう。
誤解を恐れずに言うと「そのパラメータを変えたときに、出力結果に平均どの程度の影響を与えるか」というパラメータの性質を数量化したものです。すなわち、フィッシャー情報量の大きいパラメータは、出力結果に対して大きな情報量を持ち、重要なパラメータであると考えることができます。
フィッシャー情報量の計算方法:
$$\mathbf{F}(\boldsymbol{\theta})=\mathrm{E}_{\mathbf{y}}\left[\left(\frac{\partial \log p(\mathbf{y} | \mathbf{x} ; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}}\right)\left(\frac{\partial \log p(\mathbf{y} | \mathbf{x} ; \boldsymbol{\theta})}{\partial \boldsymbol{\theta}}\right)^{T}\right] $$
提案手法
とは言ってもいきなりフィッシャー情報量に基づいてパラメータを削っていくわけではありません。まず重みの大きさの小さいものを除きます。ニューラルネットの重みの多くはゼロに近く、重みが小さいときは、そのフィッシャー情報量を推定するのは困難1であるためです。
CNNにおけるFC層の各重みに対して出力結果とのフィッシャー情報量を計算し、小さいものを削除します。
更に残りの重みのフィッシャー情報行列対角成分でk-meansクラスタリング(要するにランキング)し、意味のなさそうなものを低ビットで表現することで更に削減を図ります。
理論的考察
フィッシャー情報量という言葉は聞き慣れませんが、実は有名なoptimizerである Adam には フィッシャー情報量の考え方が用いられています。

論文中にあるAlgorithm 1のWhileループ内4,6に示されるように、Adamでは傾きの自乗が減衰しながら更新されていますが、(損失関数が交差エントロピーロスである場合は)これがフィッシャー情報量に一致します。
そのため、この論文中ではNNの訓練にAdam optimizerを使用し、収束したときのAdamの内部パラメータを重み削減に直接利用しています。
結果
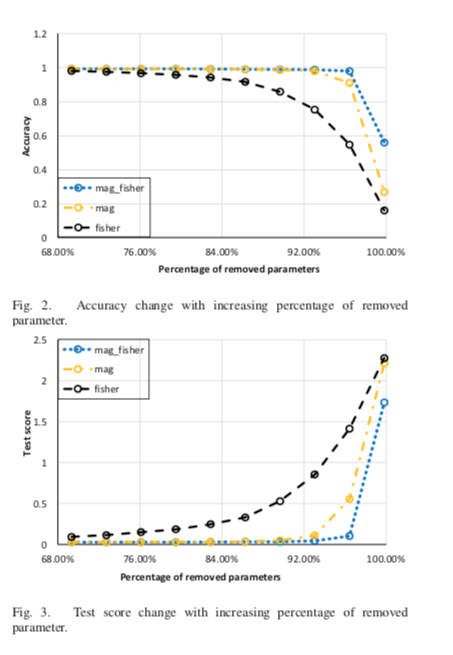
図3で一番性能低下を免れている青色のグラフは、重みの大きさに基づいて、続いてフィッシャー情報量に基づいて重みを削除したモデルです。
論文中では「〇〇%の重みを削除しても性能があまり低下しなかった」ということが盛んに喧伝されていたように思われますが、その数字は削減する前のもともとのモデルを大きくすれば水増し可能な気がするので、むしろ重みの大きさだけに基づいて重みを削除したオレンジ色のグラフに比べて性能が少し向上しているところを評価するべきでしょう。
まとめ
この論文では、フィッシャー情報量に基づいてニューラルネットを枝刈りし、高速化するという研究でした。これを実用目的に実装する人は少ないかもしれませんが、Adamの2乗移動平均$v$がフィッシャー情報量に対応していること、したがってAdamで訓練したNNが収束した時その$v$は重みのフィッシャー情報量に収束していると考えられることという知識2は知っていて損はないと思います。読んでいただきありがとうございました。
なお、本記事はMETRICAの勉強会向けに作った資料を修正したものです。