気象庁LFMGPVの積算降水量の差をとると負の時間降水量を生じることがある

2024/6/18追記

気象庁の数値予報解説資料集(令和5年度)で「4.6 プロダクトに関する参考情報」に「GRIB2 形式配信資料で積算降水量の差を取ると稀に負の値を生じることについて」の追記が行われました。本記事の内容について書かれているので、こちらも合わせて参照していただければと思います。

はじめに

気象業務支援センター経由でGRIB2形式で配信されている、気象庁局地数値予報モデル(LFM)の格子点値データ(GPV)には、初期時刻からの積算降水量が格納されている。積算降水量の差から時間降水量を計算すると、特定の時刻に負の値をもった領域が広がることが確認された。

実用上は、降水量が負になる場合は0に置き換えて処理すればよいと考えられるかもしれない。しかし、例えばテレビやインターネットニュースなどで1時間降水量のアニメーションを表示する場合、ある特定の時刻になったときのみ弱い降水域（例えば0.3〜1mmなど）が消滅し、視聴者に違和感を与えるなどの不都合が生じている。

この記事では、この現象が生じる原因を調査した。またモデルから直接出力されるNuSDaS形式のデータを用いて同様の現象が生じるかも調査した。

データ

NuSDaS形式データ

気象庁内部では、数値予報モデルの出力結果の格子点データ(GPV)は、NuSDaS形式と呼ばれる形式で格納されている¹。

LFMのNuSDaS形式データの座標はランベルト正角円錐座標であり、格子点数は1581×1301、入手したデータの出力時間間隔は1時間毎である²。

データは2UPPと呼ばれるパッキングが行われている。パッキングとは線形変換によってデータをビット数の少ない整数型に近似的に変換することによって使用ビット数を減らすことを指す。2UPPはデータを16ビット符号なし整数で表現した後(ここまでは2UPCというパッキングと同一)、整数列を複合差分圧縮したものをファイルに格納する。16ビット符号なし整数で保存するパッキング(2UPC)は、データ列を$y_i$、ファイルに書くべき整数列を$n_i$としたとき、次のようにエンコードされる：

b = \min_i(y_i) \;\;\; (1) \\
a = \frac{\max_i(y_i) - \min_i(y_i)}{65532} \;\;\; (2) \\
n_i = \mathrm{floor} \left[\frac{y_i - b}{a} + 0.5 \right] \;\;\; (3)

これに対して

y_i' = a n_i + b \;\;\; (4)

とデコードすることで、元の $y_i$ に近い浮動小数点数 $y_i'$ が得られる。

以降の解析では、Pythonで読み込みを行う都合上、NuSDaS1.4ライブラリを用いてNuSDaS形式からnetCDF形式へと変換したものを用いている。netCDFには16ビット符号なし整数として(4)式でいうところの $n_i$ をそのまま書き込み、scale_factor属性に $a$、add_offset属性に $b$ を設定している。空間座標については、等緯度等経度格子への内挿は行わず、ランベルト正角円錐座標のまま書き込んでいる。

GRIB2形式データ

気象業務支援センターから配信されているGRIB2形式のLFMGPV³について説明する。このデータは民間事業者等の気象庁の外部で利用することを目的としたもので、気象庁内でNuSDaS形式のモデル出力データから内挿等を行い変換されたものである。

積算降水量を含む地上面データは経度0.025°、緯度0.020°の等緯度等経度格子で提供されている。データの範囲は120-150°E、22.4-47.6°Nであるが、モデルの計算領域外の部分については資料値が欠落している。東西1261格子、南北1201格子であるが、領域外の格子点を除くと全部で1396307格子となる。時間間隔は30分ごとで10時間先までの予報がある。

データは単純圧縮（simple packing compression）により格納されており、元のデータ $Y$ は次の式で復元できる。

$$ Y = (R + X \times 2^E)/10^D ;;; \mathrm{(5)}$$

ここで、$E$ は二進尺度因子、$D$ は十進尺度因子、$R$ は参照値、$X$ は圧縮された値（符号なし整数）である。$X$ のビット数は第5節20オクテットに書かれているとおり12ビットである。$R, E, D$ は可変である。

以降の解析では、wgrib2コマンドを使用してnetCDF形式に変換したものをPythonで読み込んでいる。変換されたnetCDFには、(5)式でいうところの $Y$ の値が32ビット浮動小数点数として格納されており、scale_factor属性やadd_offset属性は用いられていない。

結果

2020年7月9日15UTC初期値のデータを対象に予報時間が7時間から10時間の間について、パッキングの係数、および時間降水量の空間分布とヒストグラムを調べた。これ以外の初期値や予報時間についても同様の結果が得られる。

パッキングの係数

NuSDaS形式データのパッキングの係数を調べたところ表1のようになった。積算降水量の領域内の最小値は0であるため、式(1)より $b = 0$ である。また $a$ は式(2)より最大値を65532で割った値となっている。$a$ は表現できる最小の正数であり、表現できる数値の刻み幅と言い換えられる。この値は時刻毎に異なる値をとる。

表1 予報時間毎のNuSDaS形式データの最小値・最大値およびパッキングの係数 $a, b$

予報時間	最小値	最大値	$a$	$b$
7	0	484.5097	0.007393	0
8	0	520.3164	0.007940	0
9	0	534.9923	0.008164	0
10	0	539.0060	0.008225	0

GRIB2形式データの積算降水量について、パッキングの係数の値を調べたところ、表2のようになった。表にない時刻も含めてどの時刻も $R = 0, D = 0$ であり、$E$ は $X$ の最大値($=2^{12}$) で $Y$ の領域内の最大値を表現できるような最も小さな値が選ばれるようである。例えば $Y$ の最大値が 1000 である場合、表現出来る最大値が $1024 = 2^{12} \times 2^{-2}$ となるように $E = -2$ が選ばれる。$2^E$ は表現できる最小の正数であり、表現できる数の刻み幅と言い換えられる。予報時間が8時間と9時間の間で $2^E$ は0.125から0.25に増加しており、7時間から8時間の間や、9時間から10時間の間は変化していない。

表2 予報時間毎のGRIB2形式データの最小値・最大値およびパッキングの係数 $R, E, D$

予報時間	最小値	最大値	$R$	$E$	$D$	$2^E$
7	0	479.8750	0	-3	0	0.125
8	0	511.0000	0	-3	0	0.125
9	0	526.5000	0	-2	0	0.25
10	0	532.0000	0	-2	0	0.25

空間分布

図1に初期時刻から9時間先までの積算降水量を示す。データの範囲の違いを除き、NuSDaS形式とGRIB2形式で等価であることが確認できる。なお、領域内の最大値がNuSDaS形式のほうがGRIB2形式よりも大きいのは、領域の違いによるものではなく、等緯度等経度格子への内挿処理によるものだと考えられる。

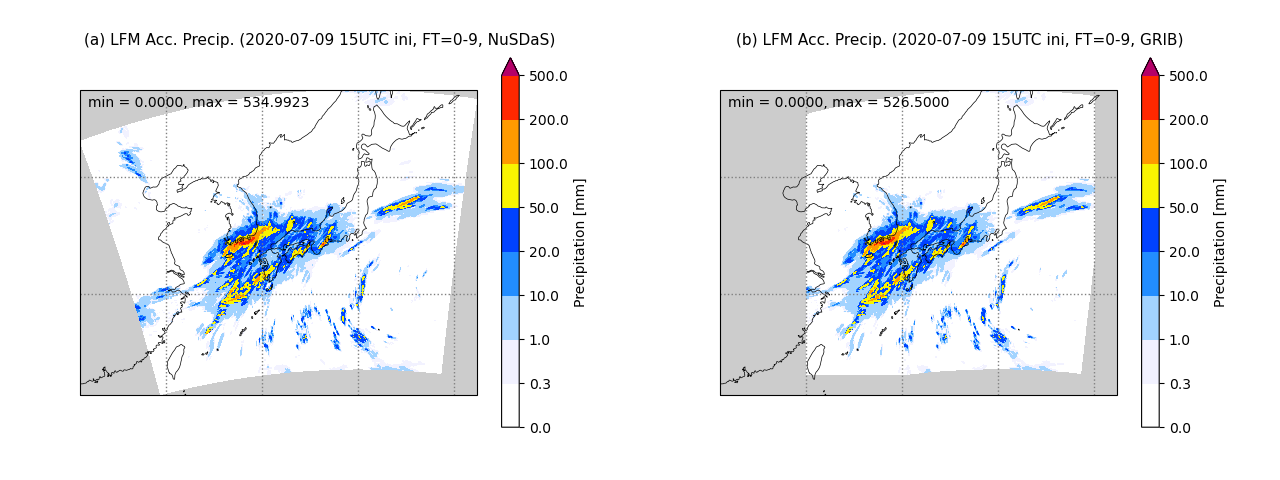
図1 LFMの初期時刻から9時間先までの積算降水量。図中の左上に領域内の最小値と最大値を示している。(a)はNuSDaS形式、(b)はGRIB2形式のデータから作図した。

積算降水量の差から計算した1時間降水量を図2-4に示す。図2は予報時刻が7時間先から8時間先までについて示している。図2の(a)と(b)を比較すると、三陸沖・北海道の東・千島近海などにNuSDaS形式データでは見られない0.0625〜0.125mmの散在した降水域が見られている。またNuSDaS形式データの時間降水量の最小値が-0.0133、GRIB2の時間降水量の最小値は-0.1250となっているが、その面積は小さく図からは降水量が負の領域が広がっている様子は確認できない。

図3の予報時刻が8時間先から9時間先までの1時間降水量ついては、図2とは異なる特徴を持っている。図3(b)をみると三陸沖・北海道の東・千島近海では-0.125mmの負の降水量の領域が広がっていることが確認できる。また東シナ海や日本の南など降水域の周辺部について、0.125mmの降水量の領域が連続的に広がっている。

図4は予報時刻が9時間先から10時間先までの1時間降水量を示しているが、図2とほぼ同じ傾向である。

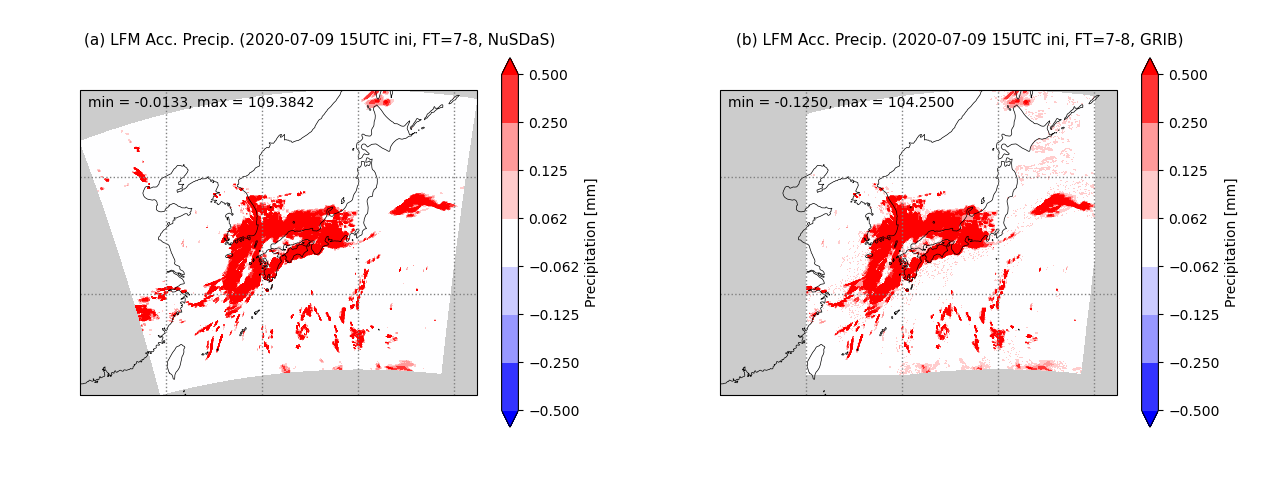
図2 LFMの予報時間が7時間先から8時間先までの1時間降水量。図中の左上に領域内の最小値と最大値を示している。(a)はNuSDaS形式、(b)はGRIB2形式のデータから作図した。

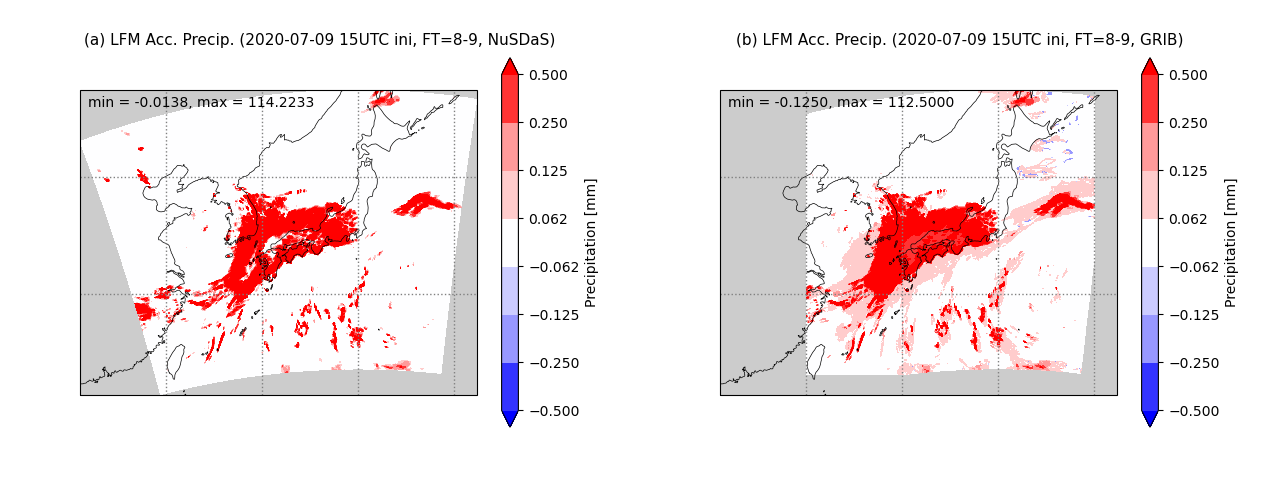
図3 図2と同じ、ただし予報時間が8時間先から9時間先について。

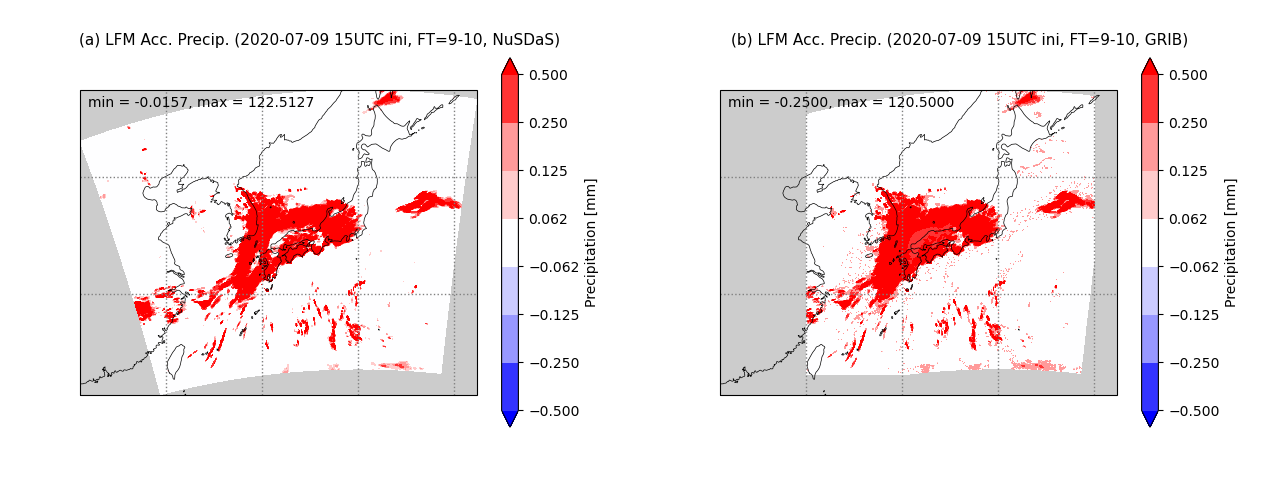
図4 図2と同じ、ただし予報時間が9時間先から10時間先について。

ヒストグラム

負の降水量を持つ格子点がどれだけ存在するのかを詳しく調べるために、0付近の降水量についてヒストグラムを描画した。結果を図7-9に示す。

NuSDaS形式データについて見ると、どの時刻についてもヒストグラムの形は同様である（図7(a), 図8(a), 図9(a)）。負の値についてみると、-0.009mm以下の格子点が約10点、-0.009から-0.001mmの格子点が約$10^5$点存在する。

GRIB2形式データについては、時刻ごとにヒストグラムに異なる特徴が見られた。予報時間7-8時間（図7(b)）では、$2^E$が0.125であるため、差は0.125の整数倍の値をとる。-0.125mmの格子点は$10^3$点、+0.125mmの格子点は$10^5$点存在する。予報時間8-9時間（図8(b)）では$2^E$が0.125から0.25へと変化しており、-0.125mmの格子点は+0.125mmの格子点と同程度の$10^5$点存在する。予報時間9-10時間（図9(b)）では、$2^E$が0.25であるため、差は0.25の整数倍の値をとる。予報時間7-8時間の場合と同様、-0.25mmの格子点は$10^3$点、+0.25mmの格子点は$10^5$点存在する。

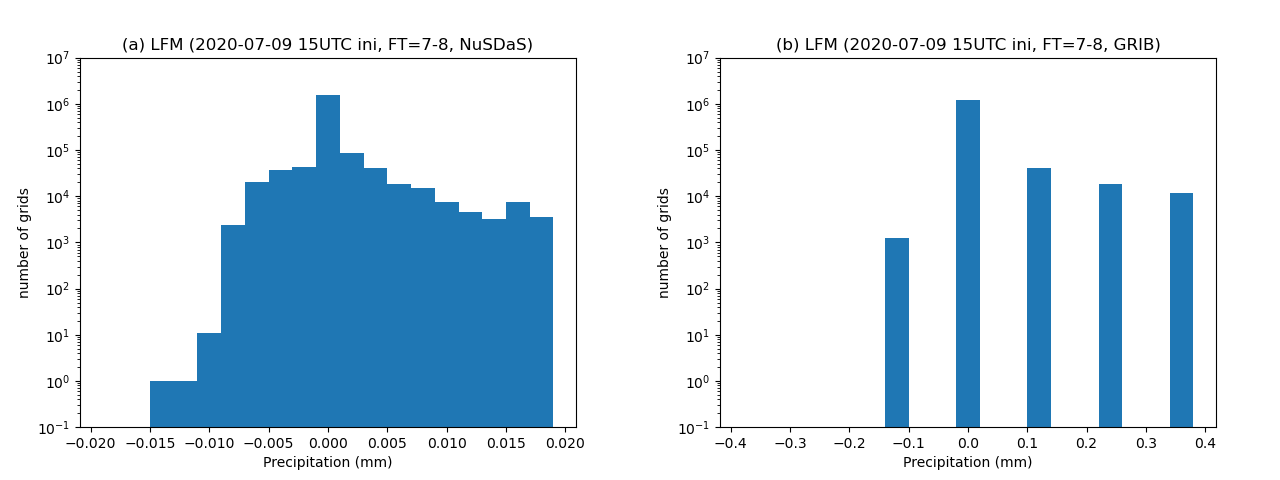
図5 LFMの予報時間が7時間先から8時間先までの1時間降水量のヒストグラム。縦軸は格子点数、横軸は降水量を表す。(a)はNuSDaS形式のデータについてで、-0.019から0.019までを表示しており、ビン幅は0.002である。(b)はGRIB2形式のデータについてで、-0.38から0.38までを表示しており、ビン幅は0.04である。

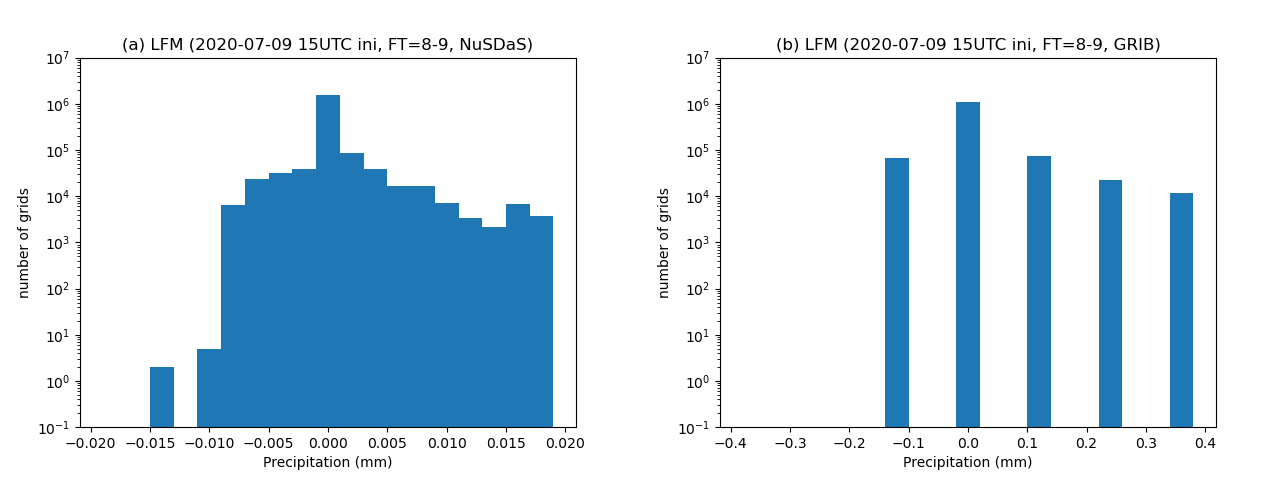
図6 図5と同じ、ただし予報時間が8時間先から9時間先について。

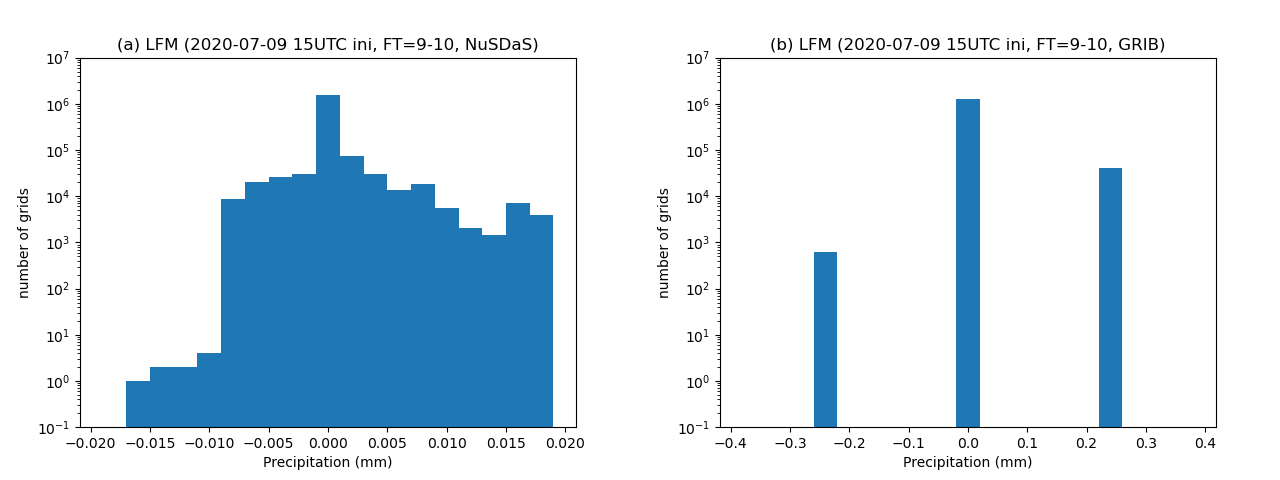
図7 図5と同じ、ただし予報時間が9時間先から10時間先について。

考察

NuSDaS形式データ

浮動小数点数がパッキングされるとき、切り捨てまたは切り上げが行われることで、実際の値よりも $\pm a/2$ の範囲で誤差が生じる。したがって、積算降水量の差から時間降水量を計算すると、実際には積算降水量が変化していない場合でも、$\pm a$ 程度の変化が生じうる。今回の場合は $a \simeq 0.008$ であるから、図5(a)のヒストグラムのうち-0.009から-0.001の間の $10^5$ 点については、パッキングの影響で説明できる。一方で、図5(a)のヒストグラムのうち-0.009以下の約10点についての理由はこれでは説明できず、原因は不明である。

NuSDaS形式データでも負の降水量が生じてはいるが、その大きさは0.01mm程度であり、描画されうる降水量の最小値（0.3mm程度）よりも十分小さく、地図上にプロットしてもその影響は確認できない(図2(a))。これは16ビット符号なし整数でパッキングされていることで、降水量0mmから500mmまでを65536段階で値を表現できることが一因となっている。

GRIB2形式データ

GRIB2形式の場合、積算降水量の最大値が2のべき乗を超えるとパッキングの係数が変化するため、その前後の差をとって時間降水量を計算する場合とそうでない場合とで異なる振る舞いをする。

パッキングの係数が異なる積算降水量の差をとる場合、引く積算降水量のパッキングでの刻み幅を $2^E$ とすると、$\pm 2^E$ の誤差が生じうる。実際に図6(b)のヒストグラムを見ると、-0.125mmと+0.125mmどちらも $10^5$ 点程度存在している。図3(b)の平面図で見られる負の降水量の領域も、このヒストグラムの-0.125mmの部分に対応しており、パッキングによる影響であると考えられる。12ビット符号なし整数でパッキングされる場合、4096段階で表現できる最小値が0.125mmや0.25mmといった比較的大きな値となるため、1mmより小さい閾値を用いて弱い降水を描画する場合には影響が出やすいといえる。

一方でパッキングの係数が変化しない場合についても、図5(b)および7(b)のヒストグラムから $-2^E$ の負の値が $10^3$ 点程度存在することが分かる。図2(b)および図4(b)の平面図では、負の領域が広がっている様子は確認できない。この負の値が生じる原因については調査していないが、モデル変数→NuSDaS→GRIBと変換する中で2回パッキングを行うことにより生じる誤差である可能性がある。

まとめ

GRIB形式データを用いて、積算降水量の差から時間降水量を計算すると、特定の時刻に負の値をもった領域が広がる理由を調査した。積算降水量の最大値が2のべき乗を超えるとパッキングの係数が変化するため、負の値の領域が生じることが分かった。この負の値の大きさは、12ビット符号なし整数でパッキングしているため比較的大きく、1mmより小さい閾値を用いて弱い降水を描画する際に影響がでることが分かった。一方、NuSDaS形式の場合、負の降水量が生じるものの値は小さく、描画時の影響はないことがわかった。

筆者はLFMGPVだけでなく全球モデル(GSM)のGPV⁴でも同様の負の値が発生することを確認している。GSMの場合は予報時間が132時間と長く、初期時刻からの積算降水量が多くなり、負の値の絶対値がより大きくなるため、問題はより深刻である。一方、メソモデル(MSM)のGPV⁵については、降水量が初期時刻からの積算降水量ではなく前1時間降水量として格納されているため、ここで述べた現象は発生しない。

この現象を防ぐには、MSMGPVのように時間降水量として格納することが挙げられる。またGRIBのパッキングに用いるビット数を12ビットから16ビットへと増やすことで、データ量は多くなるものの影響を軽減することが可能である。

謝辞

GRIB2形式のLFMGPVデータは気象業務支援センターから取得した。NuSDaS形式のLFMGPVデータは気象庁の気象過去データの利用環境（令和2年度）という枠組みで取得した。

1. 気象庁 (2020): NuSDaS (数値予報標準データセットシステム) バージョン 1.4-2 ↩

2. https://www.data.jma.go.jp/developer/past_data/app/nusdas_format_msm_lfm.pdf ↩

3. 気象庁予報部 (2020): 配信資料に関する仕様 No.12701 ～局地数値予報モデルGPV～ https://www.data.jma.go.jp/suishin/shiyou/pdf/no12701 ↩

4. 気象庁予報部 (2020): 配信資料に関する仕様 No.12501 ～全球数値予報モデルGPV～ https://www.data.jma.go.jp/suishin/shiyou/pdf/no12501 ↩

5. 気象庁予報部 (2020): 配信資料に関する仕様 No.12601 ～メソ数値予報モデルGPV～ https://www.data.jma.go.jp/suishin/shiyou/pdf/no12601 ↩