星の軌道予想（カオスシミュレーション）

#導入
シンプレティック積分法によって星の運動が計算できるという本を読んだのでプログラミングの練習として実装してみた。

#理論
シンプレティック積分法とは1900年代に登場し発展した新しい数値シミュレーション法であるが、その導出方法が特殊なことからいまだあまり普及していない。

時刻tにおける物体の位置q(t)と速度v(t)の時間変化は、大抵の問題において次のような形式の運動方程式に支配される。

\frac{d}{dt}\Biggr(\begin{matrix}q\\v\end{matrix}\Biggr)=D_H\Biggr(\begin{matrix}q\\v\end{matrix}\Biggr)

さらに時間微分することで

\Biggr(\begin{matrix}q(t)\\v(t)\end{matrix}\Biggr)=exp(tD_H)\Biggr(\begin{matrix}q(0)\\v(0)\end{matrix}\Biggr)

という式になる。この式は初期値（q(0),v(0)）を決めておき、これに時間演算子exp(tDH)をかけると未来の運動状態が得られるというものである。

ここで時間推進演算子は、運動エネルギーの要素DKと重力相互作用の効果による要素DUの和で与
えられるので、時間推進演算子は次のような式で表される。

\exp(tD_H)=exp[\Delta t(D_H+D_U)]

と書き表される。この右辺を各要素に分解することを考えると指数関数をテイラー展開してのように表わせる。

\exp[\Delta t(D_H+D_U)]\simeq exp(\Delta t D_K)exp(\Delta t D_U)

となる。さらにこの式を精度を高めtの2次式でテーラー展開すると、次のような式となる。

\exp[\Delta t(D_H+D_U)]\simeq exp(\frac{\Delta t}{2}D_K)exp(\frac{\Delta t}{2}D_U)

ここで上記の式のexp⁡(∆tDK )は運動エネルギーによる物体の時間推進を表す。すなわち、自由空間上での等速直線運動である。この運動について速度は一定不変であり、v(t)=v(0)が成り立つ。また位置qについても厳密に計算することができる。移動距離＝速さ×移動時間より、q(t)=q(0)+v(0)tとなる。よって、

exp(tD_K)\Biggr(\begin{matrix}q(0)\\v(0)\end{matrix}\Biggr)=\Biggr(\begin{matrix}{q(0)+v(0)\Delta t}\\{v(0)}\end{matrix}\Biggr)

となる。
また、exp⁡(∆tD_U)は重力fがもたらす速度vの時間発展を表す。重力は物体の速度vによらないので、力fは定数となる。なお、今度は逆にqが一定値となり、q(t)=q(0)が成り立つ。v(t)についても、厳密に計算することができる。速度＝初期速度＋加速度×移動時間と、力＝質量×加速度と組み合わせて考えると、v(t)=v(0)+t×f/mとなる。よって、

exp(tD_U)\Biggr(\begin{matrix}q(0)\\v(0)\end{matrix}\Biggr)=\Biggr(\begin{matrix}{q(0)}\\v(0)+\Delta t\frac{f}{m}\end{matrix}\Biggr)

となる。以上のことより、シンプレティック積分法は上記2式で表される2種の時間発展作業を交互に行う数値積分法であるといえる。
#コード
基本的にシンプレティック積分法で計算し、星の座標をファイルに出力していくという流れである。
今回はgnuplotで軌跡をプロットできるようファイル出力したうえで、動きが見れるようgifアニメファイルも作成した。

#define  _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<math.h>

main(){
	FILE* xy;
	//3つの星の座標点を記録するファイル
	FILE* xy0 = fopen("xy0", "wt");
	FILE* xy1 = fopen("xy1", "wt");
	FILE* xy2 = fopen("xy2", "wt");

	double G = 4;  //重力定数
	int N = 3;		 //星の数
	float M = 1.0;   //星の質量

	double pi = 3.14159265359;
	int i, j, k, l;
	double kaku;
	double r, fx, fy;
	double t, dt;

	char filename[50000];

	FILE* fp3 = fopen("script", "w");	  // アニメーション作成用　gnuplot
	fprintf(fp3, "set terminal gif animate optimize delay 2 loop 1 size 1280,960\n");
	fprintf(fp3, "set   output    ' ANIMA2.gif ' \n");
	fprintf(fp3, "set  xrange[-2:2] \n");
	fprintf(fp3, "set  yrange[-2:2] \n");
	for (j = 1; j< 4000; j++) fprintf(fp3, "plot  '%d       '\n pause 0\n", j);
	fprintf(fp3, "set out\n");

	double x[3], y[3];
	double v_x[3], v_y[3];
	double f_x[3], f_y[3];

	float teisu_u[2], teisu_k[2];
	teisu_k[0] = 0.5;
	teisu_k[1] = 0.5;
	teisu_u[0] = 0.0;
	teisu_u[1] = 1.0;

	for (i = 0; i < N; i++){
		kaku = 2.0*pi*i / N;
		v_x[i] = -sin(kaku);
		v_y[i] = cos(kaku);
		x[i] = cos(kaku);
		y[i] = sin(kaku);
	}

	fprintf(xy0, "%f  %f\n", x[0], y[0]);
	fprintf(xy1, "%f  %f\n", x[1], y[1]);
	fprintf(xy2, "%f  %f\n", x[2], y[2]);

	t = 0.0;
	dt = 1.0 / 300.0;

	for (i = 1; i < 50000; i++){
		t = t + dt;

		for (k = 0; k < 2; k++){

			for (j = 0; j < N; j++){
				f_x[j] = 0.0;
				f_y[j] = 0.0;
			}
			for (l = 0; l < N; l++){

				for (j = l + 1; j < N; j++){
					r = sqrt((x[l] - x[j])*(x[l] - x[j]) + (y[l] - y[j])*(y[l] - y[j]));
					fx = -G*M*M*(x[l] - x[j]) / (r*r*r);
					fy = -G*M*M*(y[l] - y[j]) / (r*r*r);
					f_x[l] = f_x[l] + fx;
					f_y[l] = f_y[l] + fy;
					f_x[j] = f_x[j] - fx;
					f_y[j] = f_y[j] - fy;
				}
			}

			for (j = 0; j < N; j++){
				v_x[j] = v_x[j] + dt*teisu_u[k] * f_x[j] / M;
				v_y[j] = v_y[j] + dt*teisu_u[k] * f_y[j] / M;
			}
			for (j = 0; j < N; j++){
				x[j] = x[j] + dt*teisu_k[k] * v_x[j];
				y[j] = y[j] + dt*teisu_k[k] * v_y[j];
			}
		}

			fprintf(xy0, "%f  %f\n", x[0], y[0]);
			fprintf(xy1, "%f  %f\n", x[1], y[1]);
			fprintf(xy2, "%f  %f\n", x[2], y[2]);

			sprintf(filename, "%d", i);
			xy = fopen(filename, "w");
			fprintf(xy, "%f  %f\n", x[0], y[0]);
			fprintf(xy, "%f  %f\n", x[1], y[1]);
		    fprintf(xy, "%f  %f\n", x[2], y[2]);
			fclose(xy);
	}
	fclose(xy0);
	fclose(xy1);
	fclose(xy2);
}

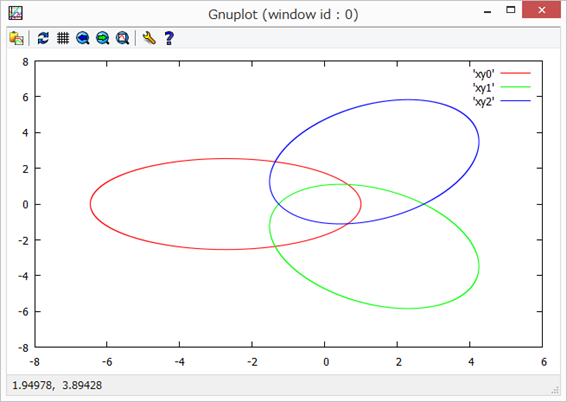
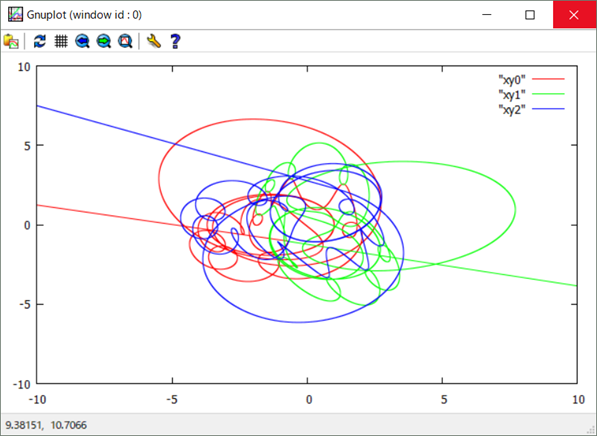
#結果
複雑な星の軌道（カオス）がみられた。

星の数：N=3　　重力定数：G=1

星の数：N=3　　重力定数：G=1.1