はじめに
何らかの他意のない画像です。
これまでの踏跡
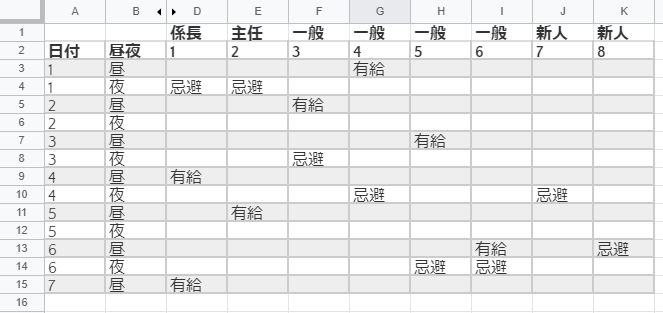
使ったデータはこちら。有給休暇を多めに入れたりしている。
目次:今回の取組課題
前回の反省
制約条件の追加
出力の確認
考察
補足:プログラム全容
前回の反省
まずは振り返って羅列していく。
・前回が割と壊滅的だったので、変数についてはortoolpyを使わず、基本に立ち返ってlpVaribalesを用いる。
・また、前回は条件式の重なりが気になったので、その辺りをもっとスッキリさせたほうが良い気がする。
・有給が複数ある場合のことをちゃんとフォローしてない
・print(ShiftScheduling)で問題に放り込んだ変数は全部見られるのだから、ちゃんとチェックすべき
というわけで、変数の見直し(lpVariable)からやっていく。
# df_rawの中身は面倒なので割愛。行ラベル2行、列ラベル2列のマルチインデックスで、ラベルの値も全部数値変換したものです(昼=0など)
df_raw = "上図のデータが入ってます"
# 元データのインデックスとカラムはリストで取得しておく
list_pm = df_raw.columns.to_list()
list_da= df_raw.index.to_list()
# 問題の定義
ShiftScheduling = pulp.LpProblem("ShiftScheduling", pulp.LpMinimize)
# 変数宣言
# x[p,m,d,a]で全パターンの0-1変数を作成する
x = {}
for p,m in list_pm:
for d,a in list_da:
x[p,m, d, a] = pulp.LpVariable("x({:},{:},{:},{:})".format(p,m,d,a), 0, 1, pulp.LpInteger)
基本に立ち返るとこうなる。
立式上、x=0ならば欠席、x=1ならば出席を意味する。
行列式にはなっていないので、都度forを回す必要はあるが、
x[p,m,d,a]の形で全て保管されるので、例えばprint(ShiftScheduling)で中身を確認した時に、
x(3,7,4,1) + x(3,7,5,0) <= 1
表記がこの様になって、「2つのxのpとmが一緒なので、同一人物についての式である」
「特定人物の4日目の夜と、5日目の昼の合算が1以下=連勤不可を指している」などが比較的読み解きやすい。
満たしたい要望は4つ有るので、最終形としては目的関数に下記のように4つの変数をぶちこみたい。
ShiftScheduling += obj1 + obj2 +obj3 + obj4
順を追って作っていく
obj1= pulp.lpSum(x)
これはもう何度も作っているし、超シンプル。
xは全シフトの出欠を示すので、obj1=26なら全体の出席は26回である。
今回は必要出勤回数が全てMin:2なので、13シフト*2人=26が理論上最小値となる。
# まず、夜勤忌避の希望を全て拾い上げる必要がある。df_rawからセルの値=1で抜き出し、その行列ラベルから
# 夜勤忌避となるp,m,d,aの組み合わせをリスト化する
list_yakin=[]
for p,m in list_pm:
df_yakin = df_raw[df_raw.loc[:,(p,m)]==1]
for i in range(len(df_yakin)):
da_yakin = df_yakin.index
list_temp = [p,m,da_yakin[i][0],da_yakin[i][1]]
list_yakin.append(list_temp)
# list_yakinを元に「夜勤忌避のときの変数の総和」を取り、これを目的関数にする
obj2 = pulp.lpSum(x[p,m,d,a] for p,m,d,a in list_yakin)
やや迂遠な気もするが、夜勤忌避を複数出した場合にも対応できるので、まあまあ良いものができた。
空のリストを用意して、後から.append()する方法を今回は多用したが、もっとスッキリした書き方がありそうな気もする。
なお、マルチインデックスの場合、dataframe.indexに多くの情報が詰められているが、
dataframe.index[0]には0行目のインデックス値がタプルで格納されており、dataframe.index[0][0]と指定すると
タプルの要素の1個めが取り出せる、と言うところがポイント。
>>>print(df_yakin)
position 1 2 0 3
member 1 2 3 4 5 6 7 8
date time
6 0 0 0 0 0 0 2 0 1
# 注記:上記は[p,m]=[6,0]の時のもの
>>>print(df_yakin.index)
MultiIndex([(6, 0)],
names=['date', 'time'])
>>>print(df_yakin.index[0])
(6, 0)
>>>print(df_yakin.index[0][0])
6
なお、「目的関数3.有給の希望が通る方が良い」についてはセルの値を1で抽出するか、
2で抽出するかしか差が無いので、ここでは割愛。補足に纏めて掲載する。
# 勤務の最大回数-最小回数を用いる。
# しかし、今回は最低出勤回数が3と決まっているので、最大値を最小化してもらえば、同じことになるはずである
obj4 = pulp.LpVariable("workcount",lowBound=0)
前回の失敗から学んだ数少ないものが、「制約条件で規定できるならば変数を変数で定義するような真似をして良いし、
それを目的関数に予め突っ込んでおいても良い」と言う事でる。
よって、今回はobj4として変数を一つ作っておき、これを目的関数に放り込むことにした。
コメントにも書いたとおり、前回の失敗の要因の一つは最小値を変数と定数の両方で定義してしまったことと考えた。
lpSum(Aさんの勤務回数)>=3
lpSum(Aさんの勤務回数)>="workcount_min"
というような立式だったが、落ち着いてみると完全に重なっている。
無論、workout_min=4になることは普通にあるのだが、作業者のばらつきを減らすことだけを考えるなら、
workcount_maxをなるべく3に近づけさせれば、それだけでおおよそ解決する話である。
分散・標準偏差は立式も面倒で、データ数が増えた時に計算が終わらない気もしているので、略!
かくして目的関数は完成した。ただ、目的関数のobj4は厳密には制約条件から定まる、というところなのである意味では未完成とも言える。
この曖昧な状態のまま進んで良いところが、ソルバーの良さであり、感覚的につかみにくいところなのだと思う。
制約条件の追加
今回の制約条件は以下の3+1とする。
- 全員必ず3回以上出勤
- 全シフトで2人以上出勤
- 連続出勤不可
+1. obj4を設定するための条件
基本的に全条件を既に作ったことが有るので、問題になるのは+1.のみである
実際、2.3.はこれまでの立式と一緒なので割愛する。
for p,m in list_pm:
ShiftScheduling += pulp.lpSum(x[p,m,d,a] for d,a in list_da) >= 3
ShiftScheduling += pulp.lpSum(x[p,m,d,a] for d,a in list_da) <= obj4
# 制約条件+1.勤務回数の偏りを減らす(最大値がobj4に格納されるようにする)
制約条件1.を設定する際、「各人の勤務回数」というのは式に含まれている。
そのため、ここに「各人の勤務回数の最大値はobj4以下」という式を足してやれば、
逆説的に「obj4は各人の勤務回数の最大値を示す」ということになる・・・なるよね、多分。きっとなる。
さて、今回は制約条件で無理をしていないのでこれ完成である。
結果や如何に。
出力の確認
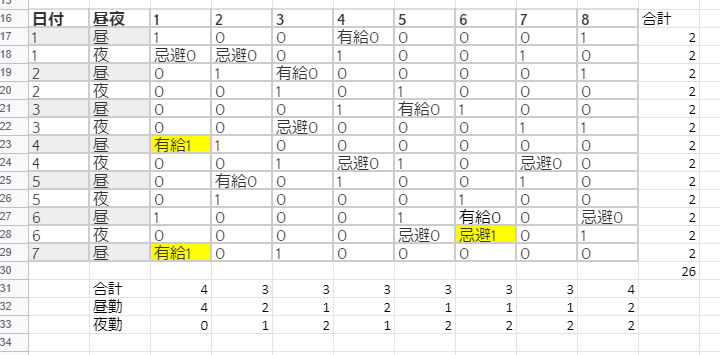
結論から書くと上表のようになった。
解けてねえじゃねえか!!!!
もうタイトルに「完全に理解した」って書いちゃったよ。困るなあ。
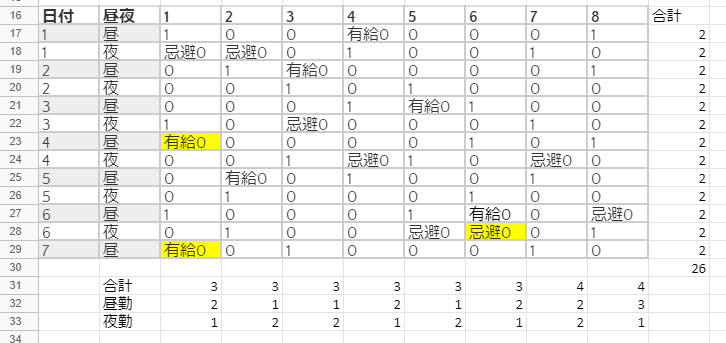
なお、これが最適解の可能性もあったので自力でちゃんと解けるパターンを見つけました。
図2
合計26、忌避0、有給0、合計の最大値4
魔法陣を解く感じでエクセルポチポチしたら解けたので、さほど難しくないはず。
さーて、考察が必要ですが、それよりも**図1の目的関数は結構高くない?**というところが気になる。
図1は合計出勤回数obj1 = 26、夜勤忌避に当たった回数obj2=1、有給に当たった回数obj3=2、
最大出勤回数obj2=4である。
つまり、ShiftScheduling.objective=26+1+2+4=33。実際の値を見てみると、
>>> print("optimality = {:}, target value = {:}".format(pulp.LpStatus[results], pulp.value(ShiftScheduling.objective)))
optimality = Optimal, target value = 30.0
組合せ最適化なんもわからん
考察
オチがついたので終わりたいところだが、もう少し粘ってみる。
まずはprint(ShiftScheduling)の再確認から。最小化を目指したMINIMIZEは・・・
MINIMIZE
1*workcount + 1*x(0,3,1,0) + 1*x(0,3,1,1) + 2*x(0,3,2,0) + 1*x(0,3,2,1) + 1*x(0,3,3,0) + 2*x(0,3,3,1) + 1*x(0,3,4,0) + 1*x(0,3,4,1) + 1*x(0,3,5,0) + 1*x(0,3,5,1) + 1*x(0,3,6,0) + 1*x(0,3,6,1) + 1*x(0,3,7,0) + 2*x(0,4,1,0) + 1*x(0,4,1,1) + 1*x(0,4,2,0) + 1*x(0,4,2,1) + 1*x(0,4,3,0) + 1*x(0,4,3,1) + 1*x(0,4,4,0) + 2*x(0,4,4,1) + 1*x(0,4,5,0) + 1*x(0,4,5,1) + 1*x(0,4,6,0) + 1*x(0,4,6,1) + 1*x(0,4,7,0) + 1*x(0,5,1,0) + 1*x(0,5,1,1) + 1*x(0,5,2,0) + 1*x(0,5,2,1) + 2*x(0,5,3,0) + 1*x(0,5,3,1) + 1*x(0,5,4,0) + 1*x(0,5,4,1) + 1*x(0,5,5,0) + 1*x(0,5,5,1) + 1*x(0,5,6,0) + 2*x(0,5,6,1) + 1*x(0,5,7,0) + 1*x(0,6,1,0) + 1*x(0,6,1,1) + 1*x(0,6,2,0) + 1*x(0,6,2,1) + 1*x(0,6,3,0) + 1*x(0,6,3,1) + 1*x(0,6,4,0) + 1*x(0,6,4,1) + 1*x(0,6,5,0) + 1*x(0,6,5,1) + 2*x(0,6,6,0) + 2*x(0,6,6,1) + 1*x(0,6,7,0) + 1*x(1,1,1,0) + 2*x(1,1,1,1) + 1*x(1,1,2,0) + 1*x(1,1,2,1) + 1*x(1,1,3,0) + 1*x(1,1,3,1) + 2*x(1,1,4,0) + 1*x(1,1,4,1) + 1*x(1,1,5,0) + 1*x(1,1,5,1) + 1*x(1,1,6,0) + 1*x(1,1,6,1) + 2*x(1,1,7,0) + 1*x(2,2,1,0) + 2*x(2,2,1,1) + 1*x(2,2,2,0) + 1*x(2,2,2,1) + 1*x(2,2,3,0) + 1*x(2,2,3,1) + 1*x(2,2,4,0) + 1*x(2,2,4,1) + 2*x(2,2,5,0) + 1*x(2,2,5,1) + 1*x(2,2,6,0) + 1*x(2,2,6,1) + 1*x(2,2,7,0) + 1*x(3,7,1,0) + 1*x(3,7,1,1) + 1*x(3,7,2,0) + 1*x(3,7,2,1) + 1*x(3,7,3,0) + 1*x(3,7,3,1) + 1*x(3,7,4,0) + 2*x(3,7,4,1) + 1*x(3,7,5,0) + 1*x(3,7,5,1) + 1*x(3,7,6,0) + 1*x(3,7,6,1) + 1*x(3,7,7,0) + 1*x(3,8,1,0) + 1*x(3,8,1,1) + 1*x(3,8,2,0) + 1*x(3,8,2,1) + 1*x(3,8,3,0) + 1*x(3,8,3,1) + 1*x(3,8,4,0) + 1*x(3,8,4,1) + 1*x(3,8,5,0) + 1*x(3,8,5,1) + 2*x(3,8,6,0) + 1*x(3,8,6,1) + 1*x(3,8,7,0) + 0
# 長すぎる。総和が入っている以上、1*x(pmda)は割とどうでもいいので、他を抜き出す。
1*workcount + 2*x(0,3,2,0) +2*x(0,3,3,1) + "中略" + 2*x(3,8,6,0)
workcount は obj4の事である。問題なし。
x(0,3,2,0)は一般社員の3番の人の2日目の昼、すなわち有給希望の日である。合ってる。
x(0,3,3,1)も同様に一般社員の3番の人の3日目の夜で、夜勤忌避の日である。
そして、今回有給回避ができていなかった「1番の人の4日目の昼」すなわちx(1,1,4,0)だが・・・
2*x(1,1,4,0)
合ってるじゃん!おかしい。というわけで次は変数を見てみる。
for v in ShiftScheduling.variables():
print(f"{v} = {pulp.value(v)}")
>>>出力
x(1,1,4,0) = 0.0
x(1,1,4,1) = 1.0
んんんんん?????
これは・・・表に整形する作業がミスっている可能性が高いぞ?
糸口が見つかったところで今回はここまで。
追記
分かった。
p,m,d,aの順番と、v in ShiftScheduling.variables()で出てくる順番が違う。
p,m,d,aはmを優先しているから先頭が(1,1)で始まるけど、
vは先頭の文字をsortしているから(0,3)で始まる。
なので、順番に整形するのではなく、ちゃんとX[p,m,d,a]の値を読み取れば答えが出る。はず。
次回やる。
プログラム全容
import pandas as pd
import numpy as np
import pulp
df="データは貼り付けが面倒だったので省略"
list_pm = df_raw.columns.to_list()
list_da= df_raw.index.to_list()
# 問題の定義
ShiftScheduling = pulp.LpProblem("ShiftScheduling", pulp.LpMinimize)
# 変数宣言
# x[p,m,d,a]で全パターンの0-1変数を作成する
x = {}
for p,m in list_pm:
for d,a in list_da:
x[p,m, d, a] = pulp.LpVariable("x({:},{:},{:},{:})".format(p,m,d,a), 0, 1, pulp.LpInteger)
# 目的関数1 全員の出勤の合計値が小さい方が良い=全変数の総和が小さい方が良い
obj1= pulp.lpSum(x)
# 目的関数2 夜勤忌避の希望が通る方が良い
list_yakin=[]
for p,m in list_pm:
df_yakin = df_raw[df_raw.loc[:,(p,m)]==1]
for i in range(len(df_yakin)):
da_yakin = df_yakin.index
list_temp = [p,m,da_yakin[i][0],da_yakin[i][1]]
list_yakin.append(list_temp)
obj2 = pulp.lpSum(x[p,m,d,a] for p,m,d,a in list_yakin)
# 目的関数3 有給の希望が通る方が良い
list_yukyu=[]
for p,m in list_pm:
df_yukyu = df_raw[df_raw.loc[:,(p,m)]==2]
for i in range(len(df_yukyu)):
da_yukyu = df_yukyu.index
list_temp = [p,m,da_yukyu[i][0],da_yukyu[i][1]]
list_yukyu.append(list_temp)
obj3 = pulp.lpSum(x[p,m,d,a] for p,m,d,a in list_yukyu)
# 目的関数4 勤務者間の労働回数はなるべく近いほうが良い
obj4 = pulp.LpVariable("workcount",lowBound=0)
# 目的関数の定義
ShiftScheduling += obj1 + obj2 +obj3 + obj4
# 制約条件1:全員必ず3回以上出勤
# 制約条件4:勤務回数の偏りを減らす(最大値がobj4に格納されるようにする)
for p,m in list_pm:
ShiftScheduling += pulp.lpSum(x[p,m,d,a] for d,a in list_da) >= 3
ShiftScheduling += pulp.lpSum(x[p,m,d,a] for d,a in list_da) <= obj4
# 制約条件2:全シフトで2人以上出勤
for d,a in list_da:
ShiftScheduling += pulp.lpSum(x[p,m,d,a] for p,m in list_pm) >= 2
# 制約条件3:連続出勤不可
list_da1 = list_da[:-1]
list_da2 = list_da[1:]
for i in range(len(list_da1)):
list_da1[i]=list_da1[i]+list_da2[i]
for p,m in list_pm:
for d1,a1,d2,a2 in list_da1:
ShiftScheduling += x[p,m, d1, a1]+x[p,m,d2,a2] <=1
# 出力
results = ShiftScheduling.solve()
print("optimality = {:}, target value = {:}".format(pulp.LpStatus[results], pulp.value(ShiftScheduling.objective)))
kekka=[]
for v in ShiftScheduling.variables():
print(f"{v} = {pulp.value(v)}")
kekka = kekka+[int(pulp.value(v))]
print(kekka[0]) #obj4の中身を見ている
kekka=kekka[1:]
kekka=pd.DataFrame(np.array(kekka).reshape(8,13).T)