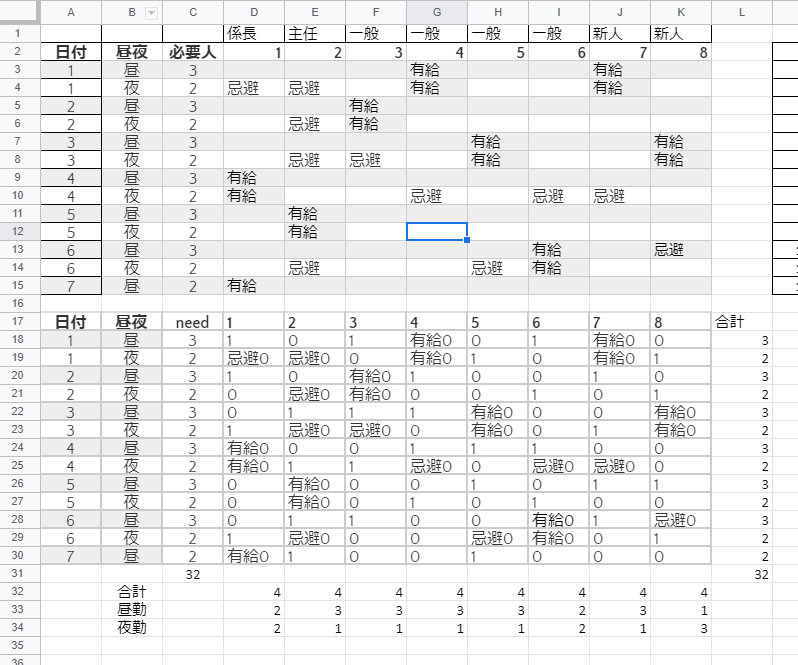
これまでの踏跡
テストデータの修正
テストデータに必要人数を追加し、必要人数のトータルが32になるように調整。
今回は8人なので、8人が4回ずつ出勤するのがベストな数に調整することで、
目的関数を問題なくクリアしているか?が容易に確認できる。
※33だとobj4が基本5となるため、かなり解くのが容易になる
制約条件の調整
まずは前回の考察で考えた制約条件の追加をしていくが、その前にリストを更新する。
list_da= df_raw.index.to_list()
list_dan = df_raw.index.to_list()
リスト名が変わっただけである。
あ、やめて。石を投げないで。
データが変わった影響で、リストの中身は132から133に増えてるんです……。
x = {}
for p,m in list_pm:
for d,a,n in list_dan: #nを追加(使わないけど足さないと動かない)
x[p,m,d,a] = pulp.LpVariable("x({:},{:},{:},{:})".format(p,m,d,a), 0, 1, pulp.LpInteger)
リストの変更に伴い、for文にnを追加。
for in list の形式は、listの全ての要素を参照しないといけないので、式中では使用していないがnも追記してある。
追加条件1. 全シフトで必要人数以上出勤
リストを修正済みであり、必要人数のデータはnに入っているので、
これまで>=2としてきたところを、>=nとすれば良い
for d,a,n in list_dan:
ShiftScheduling += pulp.lpSum(x[p,m,d,a] for p,m in list_pm) >= n
追加条件2.夜勤一回以上
単純にx[p,m,d,1]で抜き取ると、7日目夜勤がないのでエラーが出る
なのでまず、[d,1]の組み合わせを夜勤の必要回数リストとして抑えてからx[p,m,d,a]を設定すればよい。
df_yakin_min = df_raw.groupby(["action"]).get_group(1)
list_yakin_min = df_yakin_min.index.to_list()
for p,m in list_pm:
ShiftScheduling += pulp.lpSum(x[p,m,d,a] for d,a,n in list_yakin_min) >=1
マルチインデックスのindexとcolumnsの値を選び取る場合、.groupbyが便利
追加条件3. 新人だけでシフトを埋めてはいけない
ここで見つかったちょっと厄介な点として、制約条件には「>」や「!=」は使えないらしい。
「>=」「==」「<=」を使うしかないっぽい。
幸いにも今回のx(p,m,d,a)は常に整数であるため シフトの総和 >= 新人の総和+1 とすれば
シフトに入っている2人を新人2人で埋めている場合、2 >= 2+1 :False となるから制約することが可能。
この方法なら新人が3,4人となったときも同様に使える。
夜勤一回と同様に、新人の専用リストを先に作ってからfor文に入れる。
df_newbe = df_raw.groupby(["position"],axis=1).get_group(3)
list_newbe = df_newbe.columns.to_list()
for d,a,n in list_dan:
ShiftScheduling += pulp.lpSum(x[p,m,d,a] for p,m in list_pm) >= pulp.lpSum(x[p,m,d,a] for p,m in list_newbe)+1
改めて出力確認
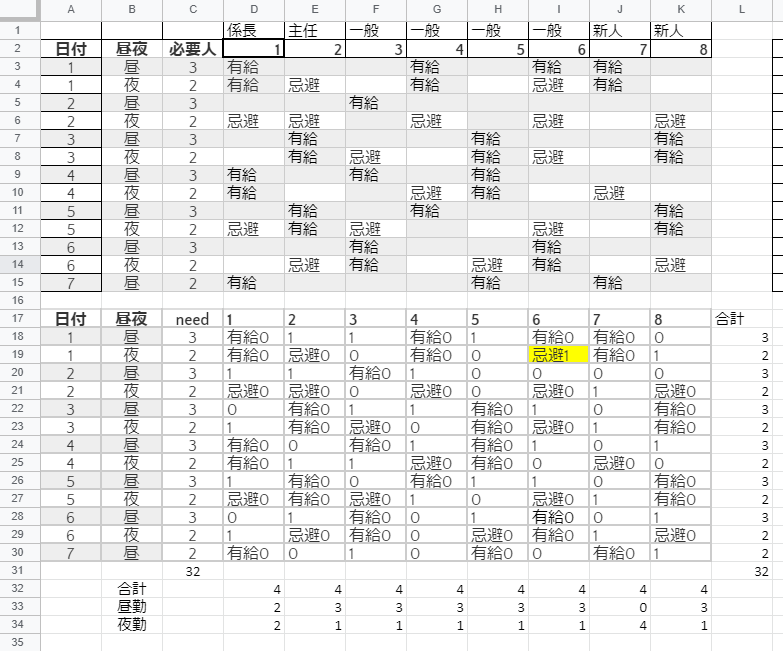
こうして制約条件を追加して再計算した結果が上記である。
出勤32回、有給・忌避への参加0回、勤務者の最大出勤回数4回で理論値36が得られている。よしよし。
制約条件作りにも慣れてきたので、かなりスムーズに行った。
よって、もうちょい突き詰めてみる。
特に気になるのは、**obj=37になる時、ソルバーはどれを優先するか?**というところなので、
データを更に厳しくしてみる。
上表:input 下表:output
まだ理論値36が崩れない。思った以上に耐えられるんだなあ。
条件の厳しさを限界まで攻める必要があるが、例えば全ての夜勤忌避など、1行で矛盾する条件を作ってしまうと後の検証ができないので、そこは注意する。
**実は君たち、働く気無いんじゃない?**ってくらい忌避と有給を増やし、遂にバランスが崩れた。
目的関数の合算は37。忌避が1箇所で破綻している。
さて、今回の本題はここから。
普通に考えると、今回の目的関数=37にするパターンは、
「忌避を1回無視する」「有給を1回無視する」「勤務回数5回が1人、4回6人、3回1人にする」の3パターンが考えられる(総数33になると、必然的に勤務回数最大も5回になるので、総数だけ増やすパターンは存在しない)。
なので、ここで重み付けを動かして検証する。
「忌避を1回無視する」は既に出ているので、他の2パターンではどのような解が得られるのか。
重み付け検証
1.夜勤忌避を許さない場合
# obj2が忌避なので、これを破ると10倍増えることにした
ShiftScheduling += obj1 + obj2*10 +obj3 + obj4
結果がこちら。忌避の次に外したのは有給が2個。obj=38。
意外な結果に。
つまり、有給1個踏み倒しや、最大勤務5回ではそもそもobj=37は実現不可能だったらしい。
---ここで私に電流走る---!!!
これ、勤務回数5回になることないんじゃね?
この勤務スケジュールを埋める作業は、要するにピクロスとかなり酷似したルールになっている。
ピクロス: https://www.nintendo.co.jp/n02/shvc/bpij/what/index.html
右の勤務表を解くことは「新人だけでのシフト駄目」「横軸は連続しても良い」など、細部に正式なピクロスとの違いはあるものの、左側のピクロスを解くのと同じようなものである。
そして今回の「忌避や有給は答えが出ないなら少しだけ無視していい」というのは、**「☓印の上に点を打っていい」ということであり、「勤務回数や総数を増やしていい」というのは、「縦軸の14を15にして良い」**ということに他ならない。
しかし、ピクロスが破綻するときは基本的に「☓印のせいで置けなくなった時」である。
14が15になっても、元々の☓の個数は変わらないし、連勤不可も変わらない。
よって、「勤務回数を増やして解決する場合」というのは、1人だけ要望無しの人がいて、その人が全部出れば解決するというような場合に限定されそうである。
普通に考えて勤務シフトを引く上であまり好ましい状況ではない。
場合によっては、「夜勤忌避と有給のどっちを優先するか?」というのは重要になりそうだが、
今の方式を拡張していった場合、総勤務回数を気にすることはあまりないのではなかろうか。
ふーむ。これはちょっと考えたほうが良さそう。
というところで今回はここまで。
大したことしてないのでプログラム全容は掲載しない。