GPU対応の最近傍探索(類似検索)ライブラリ Faiss
Facebook AI Research (FAIR)が開発したGPU対応の最近傍探索(類似検索)ライブラリ Faiss を紹介します。
個人ブログの以下の2つのエントリーの内容を1つにまとめて、Qiita用に整形したものになります。
注意点: 上記ブログ(part2)は6月に書いた記事なので、それ以降のFaiss本体のアップデートには追従していません。APIの仕様などが変更されている可能性があります。
環境
| AWS | 自宅サーバ | 共通 |
|---|---|---|
| Amazon Linux AMI release 2017.03 Intel Xeon CPU E5-2686 v4 @ 2.30GHz NVIDIA GK210GL [Tesla K80] |
Ubuntu 16.04 LTS (x86_64) Intel Core i5-2500K CPU @ 3.30GHz NVIDIA GM204 [GeForce GTX 970] |
CUDA Toolkit 8.0 GCC 4.8.3 / 5.4.0 |
導入手順は公式のREADMEを読めばわかりますし、前述のブログ内でもある程度説明しているのでここでは省略します。ブログを書いた時期はCMake対応がまだ微妙だったので、普通に依存パッケージを入れてからmakefile.incを編集後にコンパイル・インストールしていましたが、今ではCMakeでのビルドが簡単になっているかと思います。
また、FaissではC++およびPythonインタフェースを提供しています。PythonインタフェースはSWIGでC++コードから生成されているため、C++インタフェースを理解すればPythonインタフェースを利用するための学習コストはかなり小さくなるため、ここではC++で説明していくことにします。
動作確認
CPU版 C++ライブラリのビルド時にテストプログラムもコンパイルされて実行可能バイナリが生成されているのでそのまま実行できます。GPU版も用意されているのですが、これは2017/05現在、バグがあって特定のGPUだとSEGVしてしまうので完走できません。どうやらGeForce系GPU(GTX 970や1080)でのクラッシュ報告が多いようです。EC2 p2-xlargeインスタンスのTesla-K80なら大丈夫でした。
## CPU版
$ ./tests/demo_ivfpq_indexing
[0.001 s] Generating 100000 vectors in 128D for training
[0.168 s] Training the index
Training IVF quantizer on 100000 vectors in 128D
Training IVF residual
Input training set too big (max size is 65536), sampling 65536 / 100000 vectors
computing residuals
training 4x256 product quantizer on 65536 vectors in 128D
Training PQ slice 0/4
Clustering 65536 points in 32D to 256 clusters, redo 1 times, 25 iterations
Preprocessing in 0.00 s
Iteration 24 (2.32 s, search 2.10 s): objective=113338 imbalance=1.004 nsplit=0
Training PQ slice 1/4
Clustering 65536 points in 32D to 256 clusters, redo 1 times, 25 iterations
Preprocessing in 0.00 s
Iteration 24 (2.81 s, search 2.55 s): objective=113197 imbalance=1.004 nsplit=0
Training PQ slice 2/4
Clustering 65536 points in 32D to 256 clusters, redo 1 times, 25 iterations
Preprocessing in 0.00 s
Iteration 24 (3.83 s, search 3.48 s): objective=113227 imbalance=1.009 nsplit=0
Training PQ slice 3/4
Clustering 65536 points in 32D to 256 clusters, redo 1 times, 25 iterations
Preprocessing in 0.01 s
Iteration 24 (5.52 s, search 5.06 s): objective=113061 imbalance=1.004 nsplit=0
[21.231 s] storing the pre-trained index to /tmp/index_trained.faissindex
[21.233 s] Building a dataset of 200000 vectors to index
[21.705 s] Adding the vectors to the index
add_core times: 2477.588 806.523 13.101
[25.002 s] imbalance factor: 1.23894
[25.002 s] Searching the 5 nearest neighbors of 9 vectors in the index
[25.006 s] Query results (vector ids, then distances):
query 0: 1234 11667 163213 83335 13439
dis: 7.09815 9.59665 9.70155 9.80191 9.8625
query 1: 1235 76478 56663 28798 117320
dis: 7.79175 10.1169 10.4342 10.4568 10.6911
query 2: 1236 189820 80604 185497 81842
dis: 7.60428 11.0645 11.1066 11.1707 11.2591
query 3: 1237 116226 85618 36842 187787
dis: 8.03953 10.4461 10.6549 10.7921 10.7933
query 4: 1238 91514 86365 52306 69284
dis: 7.4044 10.0915 10.1178 10.1657 10.2154
query 5: 1239 143840 70772 2444 96181
dis: 7.18461 9.72012 10.2507 10.364 10.5746
query 6: 1240 72767 170354 122756 61561
dis: 7.31866 9.74185 9.94351 9.97688 10.203
query 7: 1241 30037 196333 162441 194151
dis: 8.19873 11.4148 11.6176 11.6699 11.6904
query 8: 1242 66419 10135 189152 10030
dis: 8.2098 10.8027 11.1994 11.2308 11.2371
note that the nearest neighbor is not at distance 0 due to quantization errors
テストプログラム内部で行われていることはチュートリアルを進めていけばわかるようになるのでここでは省略します。公式のチュートリアルよりもコードは綺麗な気がしますけど。。
チュートリアル
公式のチュートリアルに補足を加えながら順番に動作確認していきます。
- Getting started tutorial · facebookresearch/faiss Wiki
- faiss/docs at master · facebookresearch/faiss (Doxygen)
Faissが提供するクラスや各機能が扱うデータの型を意識しながら学んだ方がより理解しやすいと思うので、最初はC++インタフェースで試します。Pythonインタフェースは前述の通りSWIGで生成されているため、C++インタフェースが使えるようになればPythonインタフェースを使うための学習コストは少なくなります。
## g++によるコンパイルオプション例(shared library利用)
$ g++ -Wall -O2 -Wl,--no-as-needed -I/usr/include -L/usr/lib -lfaiss sample.cpp -o sample
データの準備
Faissが扱うベクトルデータは基本的に単精度(32bits)浮動小数点値を要素とした配列を用います。C++ならfloat型配列 、Python(NumPy)だと numpy.ndarray オブジェクトとなり、1つのベクトルを1行としたrow-majorな行列データとして扱うことになります。
int d = 64; // 次元数
int nb = 100000; // データベースのサイズ(格納データ数)
int nq = 10000; // 検索クエリのサイズ(クエリ数)
float *xb = new float[d * nb]; // スタックオーバーフローを防ぐためヒープ上に作成
float *xq = new float[d * nq];
for(int i = 0; i < nb; i++) {
for(int j = 0; j < d; j++) xb[d * i + j] = drand48(); // drand48() [0.0, 1.0) で一様分布する非負の倍精度浮動小数点実数値
xb[d * i] += i / 1000.;
}
for(int i = 0; i < nq; i++) {
for(int j = 0; j < d; j++) xq[d * i + j] = drand48();
xq[d * i] += i / 1000.;
}
64次元ベクトルデータをデータベース登録用に10万個、検索クエリ用に1万個それぞれ作成しています。各ベクトルの1次元目の値だけ修正してますが、検索時にその意図がわかるのでここでは気にしなくても良いです。このチュートリアルでは通常のfloat型配列で入力データを管理していますが、Faissの実装を読んでみたところ、インデックス作成時に std::vector のコンテナにデータを詰め替えています。もしOpenCVと併用するなら cv::Mat に変換するアダプタを作っておきたいですね。
インデックスの作成
データベースのインデックスを作成します。ここからはFaissのAPIを使っていきますが、インデックスの種類はたくさんあるのでここでは基本的なものをピックアップして紹介していこうと思います。
faiss::IndexFlatL2
まずは基本となる距離尺度にL2ノルム(L2距離)を利用したインデックスの作り方を確認します。
faiss::IndexFlatL2 index(d); // L2ノルムインデックスのインスタンス生成
printf("is_trained = %s\n", index.is_trained ? "true" : "false"); // is_trained = true
// 全ベクトルデータのインデックス登録
// faiss::IndexFlatL2::add(idx_t n, const float *x) , idx_t: typedef long
index.add(nb, xb);
printf("ntotal = %ld\n", index.ntotal); // ntotal = 100000
IndexFlatL2 はL2ノルムでの全探索用(Brute-force search)インデックスとなっており、入力ベクトルデータは未加工のまま全て登録します。publicなメンバとして is_trained と ntotal を参照していますが、それぞれインデックスの学習済フラグ(データ分布等を事前解析、IndexFlatL2では利用されない)、登録データ数を示しています。
検索
データの登録が終わったら検索してみます。前手順で作成した検索クエリ用データを利用してk-近傍探索を行います。
int k = 4;
{ // sanity check: search 5 first vectors of xb (データ確認用の簡易チェック)
long *I = new long[k * 5]; // 検索結果のインデックスを格納
float *D = new float[k * 5]; // 検索結果の距離(ここではL2距離)の値を格納
// faiss::IndexFlatL2::search(idx_t n, const float *x, idx_t k, float *distances, idx_t *labels) const
// 入力データ(つまりデータベースにインデックス済みの既知のデータ)5件をクエリにして検索
// k=4なのでクエリ毎に距離が近い順に4件まで検索
index.search(5, xb, k, D, I);
// print results
printf("I=\n");
for(int i = 0; i < 5; i++) {
for(int j = 0; j < k; j++) printf("%5ld ", I[i * k + j]);
printf("\n");
}
printf("D=\n");
for(int i = 0; i < 5; i++) {
for(int j = 0; j < k; j++) printf("%7g ", D[i * k + j]);
printf("\n");
}
delete [] I;
delete [] D;
}
{ // search xq (xq:事前に作成した検索クエリ用ダミーデータ)
long *I = new long[k * nq];
float *D = new float[k * nq];
index.search(nq, xq, k, D, I);
// print results
printf("I (5 first results)=\n");
for(int i = 0; i < 5; i++) {
for(int j = 0; j < k; j++) printf("%5ld ", I[i * k + j]);
printf("\n");
}
printf("I (5 last results)=\n");
for(int i = nq - 5; i < nq; i++) {
for(int j = 0; j < k; j++) printf("%5ld ", I[i * k + j]);
printf("\n");
}
delete [] I;
delete [] D;
}
delete [] xb;
delete [] xq;
- 出力結果例
I= // 検索結果のインデックス (k=4なので距離が近い順に4件、5クエリ分)
0 371 187 551 // インデックス済データなので上位1件目は当然検索クエリ自身となる
1 324 126 279
2 213 260 487
3 199 402 626
4 388 839 222
D= // 検索結果の距離の値 (昇順ソート済)
0 7.52398 7.5694 7.79739
0 7.15704 7.19868 7.25345
0 6.61889 6.96309 7.00845
0 7.001 7.11882 7.48969
0 7.14342 7.89587 7.9118
I (5 first results)= // ダミーの検索クエリ(未知データ)で同様に検索
486 287 1111 482
320 410 37 460
940 189 822 193
807 1002 388 505
657 156 95 1016
I (5 last results)=
10842 10827 9938 10004
9403 10267 10880 10330
9896 10146 10093 10361
8603 10523 10582 9895
11460 10123 11099 10876
データベースに登録したデータ、検索クエリ用のデータも全てランダムに生成したにもかかわらず、類似検索結果のインデックスに偏りがあることがわかります。ここで、データ生成時に各ベクトルの1次元目のデータだけ少し加工したことを思い出しましょう。データ配列のインデックス値に依存する数値が加算されており、検索結果にもその影響が表れていることが確認できます。
for(int i = 0; i < nb; i++) {
for(int j = 0; j < d; j++) xb[d * i + j] = drand48();
xb[d * i] += i / 1000.;
}
for(int i = 0; i < nq; i++) {
for(int j = 0; j < d; j++) xq[d * i + j] = drand48();
xq[d * i] += i / 1000.;
}
もし、データを加工しない場合は以下のような検索結果になります。
## 例
I (5 first results)=
55040 31506 25128 42339
52766 50610 38693 41096
40905 55042 24436 4212
64192 15007 95432 32551
45146 62032 44525 82328
I (5 last results)=
40461 79526 12960 79960
88504 16638 53654 1626
59759 33664 35785 835
67728 38098 19827 30085
81127 43351 79032 65174
2017/05現在のCPU版の実装では、次元数が4の倍数かつ同時検索クエリ数が20件以下の場合はSSEを使って距離計算をしてくれるようです。つまり、上記コード中の最初のsanity checkではSSEを利用、検索クエリデータ xq での検索ではインストール時に採用したBLAS実装(ここではOpenBLAS)に計算処理が委譲されます。また、マルチスレッドで処理される箇所はOpenMPを使って実装されているので大変読みやすくて助かります。
faiss::IndexIVFFlat
IndexFlatL2 をそのまま利用すると、いくらSSEやOpemMPを駆使して計算をしたとしても検索速度が遅くなってしまうため、Billion-scaleの大規模データに対応することは困難です。ここでは、入力ベクトルデータをクラスタリングしておき、検索時にはクエリデータに対応するセルおよび近隣のセルをいくつか選び出して、それらのセルに属するデータのみを最近傍点の候補として距離計算を行うことで検索時間を削減します。
# include <memory>
... 省略
auto xb = std::make_unique<float[]>(d * nb); // delete [] を排除したいのでチュートリアルを少しだけ改変
auto xq = std::make_unique<float[]>(d * nq);
... 省略
faiss::IndexFlatL2 quantizer(d);
int nlist = 100;
int k = 4;
// 転置インデックスクラス
// IndexIVFFlat(Index* quantizer, size_t d, size_t nlist_, MetricType = METRIC_INNER_PRODUCT)
// 量子化対象のインデックス、データの次元数、転置インデックスのリストサイズ、距離尺度
faiss::IndexIVFFlat index(&quantizer, d, nlist, faiss::METRIC_L2);
assert(!index.is_trained); // is_trained: false
index.train(nb, xb.get()); // ベクトル量子化、転置インデックス作成 (データベース登録対象データを利用)
assert(index.is_trained); // is_trained: true
index.add(nb, xb.get()); // データ登録
{ // search xq
auto I = std::make_unique<long[]>(k * nq);
auto D = std::make_unique<float[]>(k * nq);
index.search(nq, xq.get(), k, D.get(), I.get());
printf("I=\n"); // print neighbors of 5 last queries
for(int i = nq - 5; i < nq; i++) {
for(int j = 0; j < k; j++) printf("%5ld ", I[i * k + j]);
printf("\n");
}
index.nprobe = 10; // default nprobe is 1, try a few more
index.search(nq, xq.get(), k, D.get(), I.get());
printf("I=\n");
for(int i = nq - 5; i < nq; i++) {
for(int j = 0; j < k; j++) printf("%5ld ", I[i * k + j]);
printf("\n");
}
}
- 出力結果例
I=
10049 10147 10188 10184
9403 9750 9812 10346
10361 10184 9920 10333
9895 9946 9335 9677
10876 9647 9756 11103
I=
10842 10827 9938 10004
9403 10267 10880 10330
9896 10146 10093 10361
8603 10523 10582 9895
11460 10123 11099 10876
IndexIVFFlat は各セルの代表ベクトル(母点)を保存しておくための転置ファイル(転置インデックス)用のクラスとなっており、処理手順としてはベクトル量子化処理の学習ステップが一つ増えています(IndexIVFFlat::train)。ここではデータベース登録対象データをそのまま学習に利用していますが、別途用意したデータで学習しても良いです。publicなメンバである nprobe で検索対象のセル数を管理しており、この値を増やすと検索精度の向上と引き替えに検索時間が増えます。上記チュートリアルでは全探索と比較してnprobe=1で15 ~ 20倍、nprobe=10で3 ~ 5倍くらい検索速度が向上しました。
faiss::IndexIVFPQ
IndexFlatL2 および IndexIVFFlat を併用した場合でも、入力ベクトルデータは全て未加工でインデックス登録していました。これでは数億オーダーのデータを全てメモリ上に載せるのは現実問題として困難です(NVMe等ストレージハードウェアも急激に進歩しているのですがここでは考えないこととします)。次は、入力ベクトルデータをProduct Quantization(PQ: 直積量子化)により圧縮することでインデックスするデータ量を削減します。PQはハッシュベースの手法に替わってここ数年の論文等でよく見かけますね。Product Quantizationに関する日本語の概要説明については以下の映像奮闘記さんのエントリーが読みやすくて参考になるかと思います。
参考: 映像奮闘記: 直積量子化(Product Quantization)を用いた近似最近傍探索についての簡単な解説
クエリベクトルをM分割し、N/M次元のサブベクトルに分解する
クエリのサブベクトルと、それぞれのコードブックに記された代表ベクトル間の距離を予め計算しておく
それぞれのエントリがどのインデックスに位置しているのか確認し、2で計算した距離を参照して足し算を行う
最小距離をもつエントリを候補として提出する
... 省略
faiss::IndexFlatL2 quantizer(d); // the other index
int nlist = 100;
int k = 4;
int m = 8;
// Product Quantizationを伴う転置インデックス
// IndexIVFPQ(Index * quantizer, size_t d, size_t nlist, size_t M, size_t nbits_per_idx)
// 量子化対象のインデックス、データの次元数、転置インデックスのリストサイズ、サブベクトル数、サブベクトルの量子化ビット数
faiss::IndexIVFPQ index(&quantizer, d, nlist, m, 8); // 8 specifies that each sub-vector is encoded as 8 bits
// 転置インデックス作成のための事前学習(ベクトル量子化処理)
// ここではデータベース登録対象データを利用して学習しているが、別途用意した学習用データを用いて良い
index.train(nb, xb.get());
index.add(nb, xb.get()); // データ登録
{ // sanity check
auto I = make_unique<long[]>(k * 5);
auto D = make_unique<float[]>(k * 5);
index.search(5, xb.get(), k, D.get(), I.get());
printf("I=\n");
for(int i = 0; i < 5; i++) {
for(int j = 0; j < k; j++) printf("%5ld ", I[i * k + j]);
printf("\n");
}
printf("D=\n");
for(int i = 0; i < 5; i++) {
for(int j = 0; j < k; j++) printf("%7g ", D[i * k + j]);
printf("\n");
}
}
{ // search xq
auto I = make_unique<long[]>(k * nq);
auto D = make_unique<float[]>(k * nq);
index.nprobe = 10;
index.search(nq, xq.get(), k, D.get(), I.get());
printf("I=\n");
for(int i = nq - 5; i < nq; i++) {
for(int j = 0; j < k; j++) printf("%5ld ", I[i * k + j]);
printf("\n");
}
}
- 出力結果例
I=
0 66 283 647
1 658 421 8
2 349 1111 37
3 626 139 199
4 38 276 717
## sanity checkではインデックス済みデータをクエリとして検索しているが、検索結果1位の距離は0にはならない
D=
1.68216 6.97229 7.07727 7.20292
1.33991 6.47805 6.49344 6.8318
1.21912 6.37759 6.40442 6.42391
1.51774 5.83502 6.08639 6.62265
1.4905 6.57351 6.84026 6.85133
I=
10049 10053 9608 9938
10880 10392 10135 9812
10815 10660 10361 9747
9946 9921 9511 9246
10876 9250 10123 10869
IndexIVFPQ はPQを伴う転置ファイル用クラスです。上記チュートリアルではサブベクトル数を8、各サブベクトルは8bitsにベクトル量子化されます。つまり、元データは64(次元数)32(float)=2048bits、PQすると88=64bitsとなり32分の1のデータサイズとなります。また、各サブベクトル毎の距離計算は独立しているため並列処理とも相性が良さそうです。IndexFlatL2 による全探索(線形探索)結果を比較すると量子化の影響は見られますが、高い精度を維持できていることが確認できます。
注意点として、C++版チュートリアルのコードはGPUではなくCPUで動作します。 GPU版実装の詳細は次回パート以降に紹介する予定です。
ここからはプログラムのベンチマークも行っていくので自宅のGPUサーバをメインに使って検証します。EC2のp2.xlargeをがっつり使うと請求が怖いし、そもそもレイテンシが大きくてストレスが溜まるので。
前回の導入部分の補足としてCUDAコード部分のコンパイルにはGCCではなくNVCC(CUDAコンパイラ)を利用するので事前にインストール済みであることを確認しておきます。また、GPU製品のCompute Capabilityは3.5以降が必要となっています。
# PATHは事前に通しておく、デフォルトだと /usr/local/cuda-xxx/bin/nvcc
$ nvcc -V
nvcc: NVIDIA (R) Cuda compiler driver
Copyright (c) 2005-2016 NVIDIA Corporation
Built on Sun_Sep__4_22:14:01_CDT_2016
Cuda compilation tools, release 8.0, V8.0.44
$ nvidia-smi -L
GPU 0: GeForce GTX 970 (UUID: GPU-35bd77fd-edfe-861b-c4a6-59e9eb111aa6)
GPUでk-meansクラスタリング
まずは、公式ドキュメントにサンプルとして掲載されているGPUを利用したk-meansクラスタリングプログラムの動作確認をします。日本語での補足も簡単に入れておきます。
# include <cstdio>
# include <vector>
# include <faiss/Clustering.h>
# include <faiss/utils.h>
# include <faiss/gpu/GpuIndexFlat.h>
# include <faiss/gpu/StandardGpuResources.h>
// just generate some random vecs in a hypercube (CPU)
// クラスタリング対象のダミーデータを生成
std::vector<float> makeRandomVecs(size_t numVecs, int dim) {
std::vector<float> vecs(numVecs * dim);
// void faiss::float_rand (float * x, size_t n, long seed)
// OpenMPを利用してマルチスレッドで生成される
faiss::float_rand(vecs.data(), vecs.size(), 1);
return vecs;
}
int main(int argc, char** argv) {
// Reserves 18% of GPU memory for temporary work by default; the
// size can be adjusted, or your own implementation of GpuResources
// can be made to manage memory in a different way.
faiss::gpu::StandardGpuResources res;
int dim = 128;
int numberOfEMIterations = 20;
size_t numberOfClusters = 20000;
size_t numVecsToCluster = 5000000;
// generate a bunch of random vectors; note that this is on the CPU!
std::vector<float> vecs = makeRandomVecs(numVecsToCluster, dim);
faiss::gpu::GpuIndexFlatConfig config;
config.device = 0; // this is the default GPUデバイス番号
config.useFloat16 = false; // this is the default GPU側でFP16(半精度浮動小数点)を利用するか
faiss::gpu::GpuIndexFlatL2 index(&res, dim, config); // faiss::IndexFlatL2 のGPU版
faiss::ClusteringParameters cp;
cp.niter = numberOfEMIterations; // niter にイテレーション回数を設定
cp.verbose = true; // verbose を true にすると標準出力にイテレーション毎の処理結果が表示される
// faiss::Clustering::Clustering(int d, int k, const ClusteringParameters &cp)
faiss::Clustering kMeans(dim, numberOfClusters, cp);
// void faiss::Clustering::train(idx_t n, const float *x, faiss::Index &index)
kMeans.train(numVecsToCluster, vecs.data(), index);
// kMeans.centroids contains the resulting cluster centroids (on CPU)
printf("centroid 3 dim 6 is %f\n", kMeans.centroids[3 * dim + 6]);
return 0;
}
faiss::gpuに属するクラスについては後述しますが、faiss::gpu::GpuIndexFlatL2 は前回のエントリーで紹介した faiss::IndexFlatL2 のGPU版となっています。faiss::Clustering::train 実装内部ではイテレーション毎に現在のセントロイドをインデックスしておき、全データをクエリとして検索しています。
- コンパイル
$ nvcc \
-I/usr/local/cuda-8.0/targets/x86_64-linux/include/ -Xcompiler -fPIC -Xcudafe \
--diag_suppress=unrecognized_attribute -gencode arch=compute_52,code="compute_52" \
--std c++11 -lineinfo -ccbin g++ -DFAISS_USE_FLOAT16 \
-o gpu_kmean gpu_kmean.cpp \
libgpufaiss.a libfaiss.a -Xcompiler -fopenmp -lcublas -lopenblas
- 実行結果例
Clustering 5000000 points in 128D to 20000 clusters, redo 1 times, 20 iterations
Preprocessing in 0.74 s
Iteration 19 (238.49 s, search 225.08 s): objective=4.51621e+07 imbalance=1.012 nsplit=0
centroid 3 dim 6 is 0.468013
GPUを利用したk-meansクラスタリングは過去にもいろいろライブラリ等が出ていますし、サンプルとしてはよく見るものです。ここでの動作確認では5,000,000個のデータを20,000クラスタに分けるのに4分弱で処理できました。いまいちよく分からないのでCPU版と比較してみます。
# ちなみにCore i5-2500K(CPU)だと、
Clustering 5000000 points in 128D to 20000 clusters, redo 1 times, 20 iterations
Preprocessing in 0.73 s
^CIteration 10 (15075.25 s, search 15063.99 s): objective=4.52261e+07 imbalance=1.014 nsplit=0
./cpu_kmean 26401.24s user 5721.63s system 198% cpu 4:29:12.17 total
## 4時間経っても終わらず、、ここで断念
上記プログラムをCPUでのクラスタリング処理に変更するには、インデックスオブジェクトである faiss::gpu::GpuIndexFlatL2 を faiss::IndexFlatL2 に変えるだけです。ただし上記プログラムの設定だとCPU版の処理が一向に終わらなかったので以下のようにテストの規模を縮小することで調整しました。
- データ(128次元): 500,000
- クラス(分割数): 2,000
- イテレーション: 20
500,000個のデータを2,000クラスタに分けます。それぞれ5回計測した平均処理時間は以下の通りです。また、参考までに各製品のリリース時期も併記しています。
| CPU Intel Core i5-2500K (2011/1) |
CPU Intel Xeon E5-2686 (2016/6) |
GPU NVIDIA GM204 [GeForce GTX 970] (2014/9) |
GPU NVIDIA GK210GL [Tesla K80] (2014/11) |
|---|---|---|---|
| 511.15s | 114.10s | 5.70s | 4.85s |
前回のエントリーにも書いた通り、CPU版はOpenMPやSIMDを駆使して実装されており十分に高速です。しかしGPU版はそれと比較しても遙かに高速に動作します。また、CPUからGPUへのデータ転送は必要に応じて都度行われるため(計算に必要なデータだけGPU上に載せる)、VRAM容量を超えるような巨大なデータセットでもクラスタリング可能となっています。
さらに、FP16(半精度浮動小数点値での演算)を有効にしてGTX 970上で比較してみました。こちらも同様に5回計測した平均処理時間を載せます。
- データ(128次元): 5,000,000
- クラス(分割数): 20,000
- イテレーション: 20
| FP16無効 | FP16有効 |
|---|---|
| 228.47s | 191.76s |
| なかなか興味深い結果となりました。確かPascal世代からFP16の性能が格段に上がっていたかと思うので(1SPでFP16二つを同時演算したり)、PascalのGPUでベンチマークしてみたいところです。Facebook ResearchのレポートだとTesla P100でだいたい100秒ほどで完走するらしいです。 |
GPUを利用した検索
次はCPU版チュートリアルにある各種検索プログラムをGPU対応していきます。
GPUリソースの確保・初期化
GPUで処理するために予めGPUリソースの事前確保作業が必要ですが、生のCUDAプログラムと比較すれば十分抽象化されているので特に難しいところは無いかと思います。GPU版のヘッダファイルは faiss/gpu 以下にあります。
- faiss::gpu::StandardGpuResources
- faiss::gpu::GpuIndexFlatConfig
faiss::gpu::StandardGpuResources res;
faiss::gpu::GpuIndexFlatConfig config;
config.device = 0;
config.useFloat16 = true;
前述のk-meansのサンプルコードと同じ設定でだいたい大丈夫です。内部ではcuBLASのハンドル初期化やCUDAのストリーム生成処理等を行っています。デフォルトだとストリーム(cudaStream_t)は2本準備しているようです。
GPU版インデックスクラス
チュートリアルで紹介した各種CPU版インデックス用クラスのGPU対応は簡単なのでまとめて紹介します。
| CPU | GPU |
|---|---|
| faiss::IndexFlatL2 | faiss::gpu::GpuIndexFlatL2 |
| faiss::IndexIVFFlat | faiss::gpu::GpuIndexIVFFlat |
| faiss::IndexIVFPQ | faiss::gpu::GpuIndexIVFPQ |
const int d = 64; // dimension
## IndexFlatL2
faiss::IndexFlatL2 index(d);
## GpuIndexFlatL2 (IndexFlatL2のGPU版)
## GpuIndexFlatL2(GpuResources *resources, int dims, GpuIndexFlatConfig config=GpuIndexFlatConfig())
faiss::gpu::GpuIndexFlatL2 index(&res, d, config);
## IndexIVFFlat
const int nlist = 100; // number of inverted lists
faiss::IndexFlatL2 quantizer(d);
faiss::IndexIVFFlat index(&quantizer, d, nlist, faiss::METRIC_L2);
## GpuIndexIVFFlat (IndexIVFFlatのGPU版)
## GpuIndexIVFFlat(GpuResources *resources, int device, GpuIndexFlat *quantizer, bool useFloat16, int dims, int nlist, IndicesOptions indicesOptions, faiss::MetricType metric)
faiss::gpu::GpuIndexFlatL2 quantizer(&res, d, config);
faiss::gpu::GpuIndexIVFFlat index(&res, 0, &quantizer, false, d, nlist, faiss::gpu::INDICES_64_BIT, faiss::METRIC_L2);
## IndexIVFPQ
const int m = 8; // number of subquantizers
const int nbits = 8; // number of bits per quantization index
faiss::IndexFlatL2 quantizer(d);
faiss::IndexIVFPQ index(&quantizer, d, nlist, m, nbits);
## GpuIndexIVFPQ (IndexIVFPQのGPU版)
## GpuIndexIVFPQ(GpuResources *resources, int device, int dims, int nlist, int subQuantizers, int bitsPerCode, bool usePrecomputed, IndicesOptions indicesOptions, bool useFloat16LookupTables, faiss::MetricType metric)
faiss::gpu::GpuIndexIVFPQ index(&res, 0, d, nlist, m, nbits, true, faiss::gpu::INDICES_64_BIT, false, faiss::METRIC_L2);
2017/05現在、faiss::gpu::GpuIndexIVFPQ にはGPU版インデックスクラスのポインタを直接受け取るコンストラクタは未実装のようですので別のコンストラクタを利用しています。この場合は引数で渡す faiss::MetricType に応じたGPU版インデックスクラスのインスタンスを内部で生成/保持してくれます。前回紹介していませんでしたが距離尺度は faiss::MetricType 定数で指定するようになっており、チュートリアルではL2ノルムの紹介のみでしたが、もちろん内積(Inner Product)にも対応しています。
/// Some algorithms support both an inner product vetsion and a L2 search version.
enum MetricType {
METRIC_INNER_PRODUCT = 0,
METRIC_L2 = 1,
};
また、faiss::gpu::IndicesOptions は以下のように定義されています。これはCPU<->GPU間でのインデックス情報の転送・保存をどのような形式で行うかを指定します。
enum IndicesOptions {
/// The user indices are only stored on the CPU; the GPU returns
/// (inverted list, offset) to the CPU which is then translated to
/// the real user index.
INDICES_CPU = 0,
/// The indices are not stored at all, on either the CPU or
/// GPU. Only (inverted list, offset) is returned to the user as the
/// index.
INDICES_IVF = 1,
/// Indices are stored as 32 bit integers on the GPU, but returned
/// as 64 bit integers
INDICES_32_BIT = 2,
/// Indices are stored as 64 bit integers on the GPU
INDICES_64_BIT = 3,
};
CPU版とは異なりGPU版の各種インデックスクラスのメンバ変数はなぜかカプセル化されているみたいなので、提供されているgetter/setter経由でデータ操作を行います。GPU対応する際には忘れないようにしましょう。
// nprobe を変更する場合
index.nprobe = 10; // CPU版
index.setNumProbes(10); // GPU版
ベンチマーク
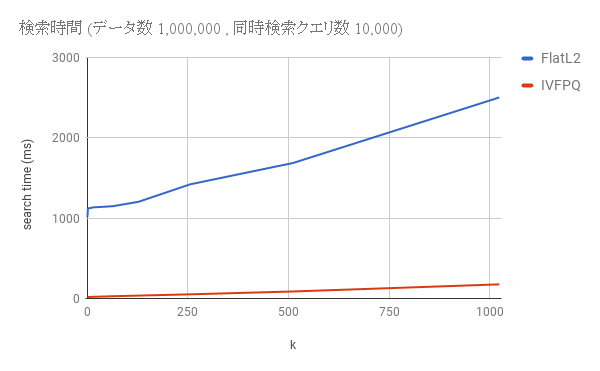
次は最近傍探索処理の測定を行います。チュートリアルのプログラムをベースにパラメータ等を調整して比較しました。論文中ではDeep1BやYFCC100Mなどの巨大なデータセットでベンチマークをしていて真似したかったんですけど、自宅のGPU開発環境だと空冷が適当なので kidle_inject が発生し、温度上昇防止のためCPU使用に制限をかけてしまいます。。ここではANN_SIFT1Mと同じ小規模データでベンチマークを行いました。
- 次元数: 128
- データ数: 1,000,000 (100万データ)
- 同時実行クエリ数: 10,000 (1万クエリ)
- インデックス: faiss::gpu::IndexFlatL2 (全探索) / faiss::gpu::IndexIVFPQ (PQ + 転置インデックス)
- 転置インデックスのリストサイズ 100、サブベクトル数 8、量子化ビット数 8、FP16有効
- 検索時のkの値: 1 ~ 1024 の範囲で変更
ベンチマーク用プログラムはここに記載するには少し長くなるのでGistにアップロードしておきます。
僕の個人開発環境だと1万クエリの上位20件を検索するのに、全探索(IndexFlatL2)の場合は約1.1秒、PQ + 転置インデックス(IVFPQ)の場合は約20ミリ秒でした。ただし、Faissの真価はbillion-scaleでの検索処理において発揮されるので、ここでのベンチマークは参考程度ということで。
また、Facebook AI Research公式の詳細なベンチマーク結果は以下を参照してください。
注意点など
GPUでの検索処理にはいくつか制限が設けられています。2017/06現在の仕様なので変更される可能性があります。
GPUテンポラリメモリ
cudaMalloc/cudaFree はコストが高い処理なので事前にある程度のメモリ領域が自動的に確保されるのですが、そのサイズをユーザー側が指定することができます。StandardGpuResources のAPIで指定できます。
faiss::gpu::StandardGpuResources res;
size_t memSize = 1073741824; // 1024MB
res.setTempMemory(memSize);
テンポラリメモリが足りないと以下のような警告が出力されます。cudaMalloc が新たに必要になってしまうから遅くなるよというヒントであって処理が継続できないわけではありません。
WARN: increase temp memory to avoid cudaMalloc, or decrease query/add size (alloc 268435456 B, highwater 268435456 B)
PQ(Product Quantization)のために内部ルックアップテーブルを準備する際にはそこそこ十分な容量を確保しておいた方が良いかと思います。
kおよびnprobe値の上限
kとnprobe値は1024が上限となっていますが、1024もあれば実用上は十分かなと思います。
# 1024以上を指定すると以下のようなエラーが発生する
Faiss assertion k <= 1024 failed in void faiss::gpu::IVFPQ::query(faiss::gpu::Tensor<float, 2, true>&, int, int, faiss::gpu::Tensor<float, 2, true>&, faiss::gpu::Tensor<long int, 2, true>&) ~ ... 省略
Product Quantizationのパラメータ
PQの実装上、量子化ビット数(サブベクトル当たりのデータサイズ)は8ビット以下、データの次元数をサブベクトル数で割った余りが0になるように調整する必要があります。今回紹介したベンチマークプログラムではデータは128次元、サブベクトル数は8、量子化ビット数は8で設定しています。
Faiss assertion bitsPerCode_ <= 8 failed in void faiss::gpu::GpuIndexIVFPQ::assertSettings_() const at GpuIndexIVFPQ.cu:436
Faiss assertion this->d % subQuantizers_ == 0 failed in void faiss::gpu::GpuIndexIVFPQ::assertSettings_() const at GpuIndexIVFPQ.cu:439
おわりに
GPU対応の最近傍探索(類似検索)ライブラリ Faissを紹介しました。GPU版はCPU版から移行修正しやすいように工夫されているので特に難しいところはなかったかなと思います。パフォーマンスは上記ベンチマーク結果の通り、大規模データに対して極めて高速に検索処理できることがわかりました。GPU版の実装は論文と併せて読み進めていますが、k-selection(選択アルゴリズム)のGPU実装(WARP SELECT)の仕組みが難しくて難航していますが、Pythonインタフェースを用いたアプリケーション寄りの開発もやってみたいと思っています。