「プログラマの数学」2章メモ#2 論理積、論理和、ド・モルガンの法則、ベン図、カルノー図、3値論理など

目次

1章 位取り記数法、0とは、指数法則など
2章 論理積、論理和、ド・モルガンの法則、ベン図、カルノー図、3値論理など
3章 (in progress)

経緯

プログラマの数学という本をおすすめされたので読んでみた。ここにメモがてら簡単に学んだことを書いていこうと思う。全部で9章分あるので章毎に分けてお送り致します。*all the credit goes to the author: 結城浩さん

論理を使って言葉の曖昧さをなくす

論理の根本には「網羅的で排他的な分類」というのがある。直感的ですが英訳するとmutually exclusive and exhaustiveあたりでしょうか。ちゃんと理解していればの話ですが。

例：
年齢が7歳以上は100円で年齢が7歳未満が0円というルールAがあったとする。そこで以下の命題(proposition)の真偽を問う。命題が正しければTrue間違っていればFalse。命題は必ずTrueかFalseの値を取る。

• カレン(13 yr old)は7歳以上である → Trueの命題
• チャーリー(7 yr old)は7歳未満である → Falseの命題
• ボブ(4 yr old)は7歳未満である → Trueの命題

「もれ」はないか？と問う

ルールAのような規則を読むとき作るときは「そのルールにもれはないか？」と自分に問うのが最優先事項。たとえば先ほどのルールAがもし「7歳より上と7歳より下」という設定だと7歳の人が該当する先がない。もしくは「7歳以上、7歳以下」だと逆に7歳の該当場所がオーバラップしている。プログラムの世界ではif/elseを使うことが多い。

複雑な命題

扱うデータの種類が増えてくるとそれだけ判断材料が増えるということなので、それに応じて命題も複雑になってくる。「何歳の男性が◯曜日に◯◯」といった具合に。

そこで否定と呼ばれる演算をつくる。(logical negation operator)
$¬A$と書くと「Aではない」という意味になる。この定義には真理値表という表を使うことが多い。

• 真理値表

A	¬A	¬¬A
true	false	true
false	true	false

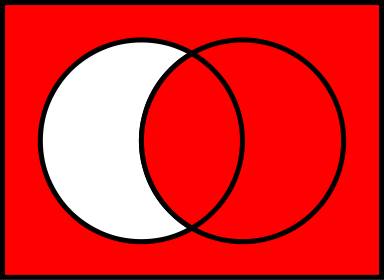
命題Aがtrueのとき、命題¬Aはfalseになる。逆もしかり。ちなみに2重否定（¬¬A）はAと等しい。もちろん、これをベン図（venn diagram）で書くことも可能。

論理積 (Logical conjunction)

"A and B" is true only if A is true and B is true.
複数の命題を組み合わせて新しい命題を作ることを論理積と呼ぶ。一般的には$A∧B$や「AかつB」とかく。$A∧B$はAとBの両方がtrueのときだけtrueになると覚えておくといい。ref: logical conjunction

• 真理値表

A	B	A∧B
true	true	true
true	false	false
false	true	false
false	false	false

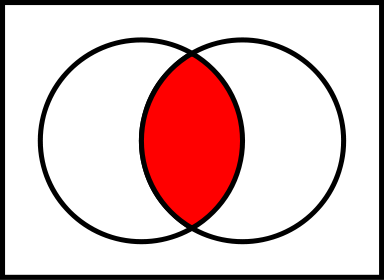
• ベン図

論理和 (Inclusive disjunction)

"A or B" is true if A is true, or if B is true, or if both A and B are true.
AまたはBという命題を作る演算は論理和と呼ばれる。$A∨B$と表記し、「AとBの少なくともどちらか片方がtrueのときにtrue」という性質を持っている。$A∨B$はAとBの少なくともどちらか片方がtrueのときにtrueになる。もしくはAとBの両方がfalseのときだけfalseになりそれ以外はtrueになる。
注意：論理和におけるorはどちらか一方という意味ではなくどちらかというと、両方に属するという意味に近い。そのためAとBの両方がtrueの場合の振る舞いが異なる。
ref: logical disjunction

• 真理値表

A	B	A∨B
true	true	true
true	false	true
false	true	true
false	false	false

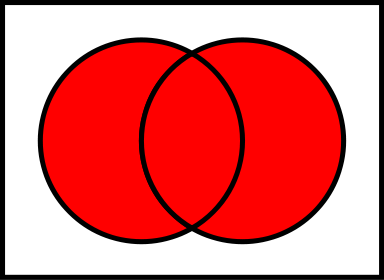
• ベン図

排他的論理和 (exclusive or)

端的にいうと、「AとBの一方だけがtrueならばtrueになるが、両方がtrueならばfalseになる」(=A or B, but not both)という命題。論理式では$A⊕B$と表記する。

• 真理値表

A	B	A⊕B
true	true	false
true	false	true
false	true	true
false	false	false

A⊕BはAとBが異なる時だけtrue

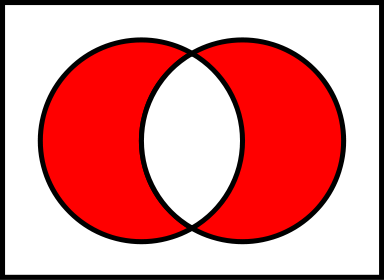
• ベン図

ref: Exclusive disjunction

等値 (A=B)

一言で言うと「AがtrueならばBもtrueである。また、AがfalseならばBもfalseである」。
その名の通り「AとBは等しい」という命題。式にすると$A=B$

• 真理値表

A	B	A=B
true	true	true
true	false	false
false	true	false
false	false	true

AとB両方がtrueのとき、A=Bはtrue
AとB両方がfalseのとき、A=Bはtrue

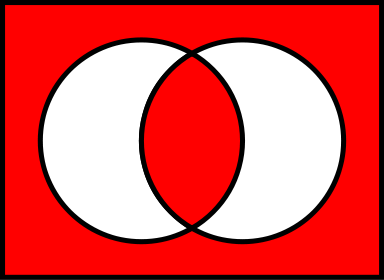
• ベン図

両方がfalseである領域、AとBの重なりあう部分はAとBの両方がtrueである範囲を表している。

ちなみに$¬(A ⊕ B) = (A = B)である。お互いの出てくる値が反対なので、ベン図からも真理値表からも簡単に理解することが出来る。

含意(AならばB)

一言で言うと「AがtrueならばBもtrueである。しかしAがfalseならば、Bはtrue/falseどちらでもよい」。
たとえば「Aさんは10歳以上である」という命題と「Bさんは4歳以上である」という命題をBとするとAならばBという命題は真。論理式は$A⇒B$

• 真理値表

A	B	A⇒B
true	true	true
true	false	false
false	true	true
false	false	true

• Aがtrueのとき、A⇒BはBがfalseの場合だけfalse
• Aがfalseのとき、A⇒Bは常にtrue

前提となっているAがtrueでBがfalseならその命題はfalseとなり、Aがfalseの場合、Bの真偽にかかわらずその命題の値はtrueになる。

• ベン図

補足

(¬A)∨B = A⇒Bである。

$A∨B$の性質は「どちらかにtrueがあれば結果もtrueになる」ので(¬A)∨Bの真理値表を作ると以下のようになる。真理値表のBと¬Aをもとにtrueの値が入っている場合はtrueにしてそれ以外をfalseにするだけだ。これをベン図で書くと上のようになる。

A	B	¬A	(¬A)∨B
true	true	false	true
true	false	false	false
false	true	true	true
false	false	true	true

(¬B)⇒(¬A) = A⇒Bである

A	B	¬A	¬B	(¬B)⇒(¬A)
true	true	false	false	true
true	false	false	true	false
false	true	true	false	true
false	false	true	true	true

これをベン図で表記すると$A⇒B$と同じ図が出来上がる。

AとBから作られる全ての演算の真理値表（流石に長過ぎたので2つに分けました汗）

常にF	A∧B	A∧(¬B)	A	(¬A)∧B	B	¬(A=B)	A∨B
F	T	F	T	F	T	F	T
F	F	T	T	F	F	T	T
F	F	F	F	T	T	T	T
F	F	F	F	F	F	F	F
0	1	2	3	4	5	6	7

(continued below)

¬(A∨B)	A = B	¬B	A∨(¬B)	¬A	(¬A)∨B	¬(A∧B)	常にT
F	T	F	T	F	T	F	T
F	F	T	T	F	F	T	T
F	F	F	F	T	T	T	T
T	T	T	T	T	T	T	T
8	9	10	11	12	13	14	15

この表には「真理値表のfalseを0、trueを1と書き換えると、左端から一列毎に0,1,2,......15」を2進法で表現した数になる。たとえば14番の表はこれに則って書くと1110となる。これを計算すると$1 * 2^3 + 1 * 2^2 + 1 * 2^1 + 0 * 2^0 = 14$となる。

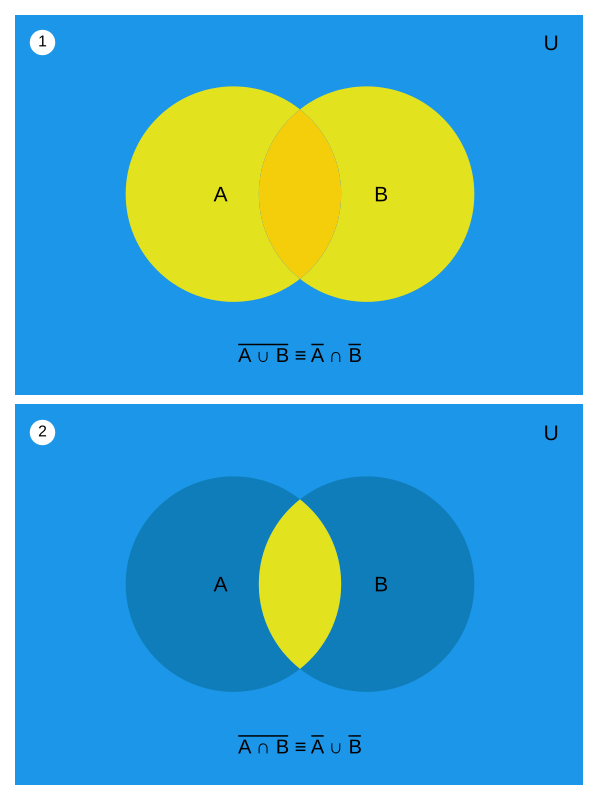
De Morgan's laws

wikiによると、

The negation of a conjunction is the disjunction of the negations.
- 否定のand(否定論理積)は否定のor(否定論理和)と等しい
- 「Aではない」または「Bではない」というのは、「AかつB」ではないことに等しい。
The negation of a disjunction is the conjunction of the negations.
- 否定のor(否定論理和)は否定のand(否定論理積)に等しい。
- 「Aではない」かつ「Bではない」というのは、「AまたはB」ではないことに等しい。

これをド・モルガンの法則(De Morgan's law)と呼ぶ。

記号に直して表記すると、
$¬(A∧B) = (¬A) ∨ (¬B)$
$¬(A∨B) = (¬A) ∧ (¬B)$

• 真理値表 真理値表でも対応していることが明白に分かる。

(¬A)∨ (¬B)	¬(A∧B)	(¬A)∧(¬B)	¬(A∨B)
false	false	false	false
true	true	false	false
true	true	false	false
true	true	true	true

ベン図に表すとこんな感じになるようです。

この辺りの動画が分かりやすく説明してくれています。

双対性

「ある論理式の中のtrueとfalse、Aと¬A、∧と∨を、それぞれ交換すると、その論理式全体を否定した論理式ができる」というもの。なぜなら双対性によりそれぞれの値は互いに対になっているから。例えば例えば論理式$A∧B$を法則に従って論理式全体を否定した論理式を作るとすると$(¬A) ∨ (¬B)$となる。

カルノー図(Karnaugh Graph)

2ランプゲームが全体を理解しやすくて面白かった。

以下の様なややこしいルールを分かりやすく表現できるでしょうか。
2ランプゲームのルール
次のいづれかになったら、ボタンを押して下さい。
a. 青いランプは消えているが、黄色いランプは光っている。
b. 青いランプは消えていて、黄色いランプも消えている。
c. 青いランプは光っていて、黄色いランプも光っている。

命題を作って考える。

命題A: 青いランプが光っている
命題B: 黄色いランプが光っている

これを以下の論理和に置き換えると

$a: (¬A)∧B$
$b: (¬A)∧(¬B)$
$c: A∧B$

になる。

つまりボタンを押すのは以下の様な式がTrueのとき

$((¬A)∧B)∨((¬A)∧(¬B))∨(A∧B)$になる

しかしこれでは複雑でわかりにくいので、カルノー図の出番。

カルノー図とは（本書の定義より）

全命題の真偽の組み合わせを2次元的に表した図のこと

どうやらカルノー図を使うと複雑な論理式もシンプルな式に書き換えることができるよう。
上の例題を参考にそれぞれの命題がとり得るすべての真偽の組み合わせに対応した図が以下になる

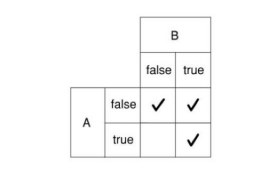
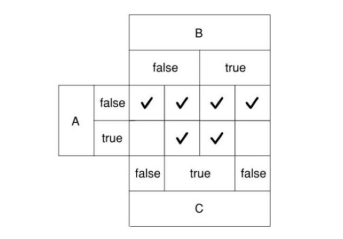
• カルノー図（本書より転載）

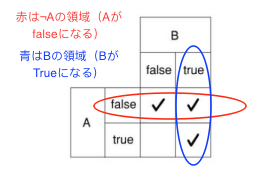
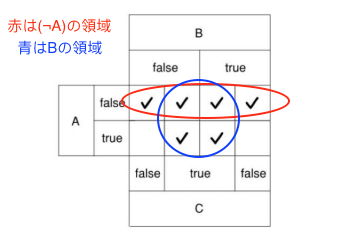
• グループ分けすると

「グループ分けするときの基準はA、B,...のfalse/trueのマスが全てチェックで埋まっているかどうかで決まる」ということを覚えておくとグループ分けがスムーズになる。
結果、$((¬A)∧B)∨((¬A)∧(¬B))∨(A∧B)$の式はカルノー図を使って$(¬A)∨(B)$へと簡略化が可能。

カルノー図(Karnaugh Graph)を使ってより複雑な命題に挑む

次のいづれかのパターンになったら、ボタンを押して下さい。
a. 青いランプは消えていて、黄色いランプも消えていて、赤いランプも消えている
b. 黄色いランプは消えているが、赤いランプは光っている。
c. 青いランプは消えているが、黄色いランプは光っている。
d. 青いランプも黄色いランプも赤いランプも光っている。
*記載されていない部分はFalseとみなして構わない

• まずは問題をもとに各命題に以下のように作り上げる。

命題A: 青いランプが光っている
命題B: 黄色いランプが光っている
命題C: 赤いランプが光っている

• カルノー図

BとCの境目にあるズレを作ることが８個マスを作る時のミソなんだとか。

• チェックマークは以下のようにつけることができる

よってチェックマークのついた領域を論理和を使って表すと$(¬A)∨C$となる。また論理式にBが存在しないことから今回のボタンを押すかどうかの判断においてはB（＝黄色いランプ）は考慮する必要がないと結論付けることができる。

未定義を含む論理

命題では必ず真偽もしくはTrue/Falseのどちらかの値をとるが現実ではエラーが原因で終了したり無限ループに陥ることもあったりとtrue/falseだけでは表すことのできない場合がある。そのためにundefinedという値を使う。直訳すると「未定義もしくは定義されていない」という意味。このundefinedを使って様々な論理式に触れてみる。

条件付き論理積（conditional and. short-circuit logical and = &&）

AとBの条件付き論理積はA&&Bを使って定義する。これをtrue/false/undefinedの３種類の値を使って真理値表を作る。

• 真理値表

A	B	A&&B
true	true	true
true	false	false
true	undefined	undefined
false	true	false
false	false	false
false	undefined	false
undefined	true	undefined
undefined	false	undefined
undefined	undefined	undefined

この真理値表から読み取れること:

• undefinedを含まない行は論理積A∧Bに等しい
• Aがtrueのとき、A&&BはBに等しい
• Aがfalseのとき、A&&Bは常にfalse
• Aがundefinedのとき、A&&Bは常にundefined

undefinedは「コンピューターの暴走」と考えるとAがundefinedならA&&Bもundefinedなのは納得がいく。ということは、A&&BはAという条件によってBを調べるかどうかを判断していると考えることが出来る（＝論理積）。これは

if (A) {
    if (B) {
       ...
    }
}

と同じことを言っていると言い換えることができる。ちなみにA&&B = B&&Aではないので交換法則は成り立たない。

if (check() && execute()) { 
    ...
}

= check()がfalseの場合、execute()は実行されない

条件付き論理和（=||）

3値論理での論理は$A||B$と定義することができる。

• 真理値表

A	B	A ll B
true	true	true
true	false	true
true	undefined	true
false	true	true
false	false	false
false	undefined	undefined
undefined	true	undefined
undefined	false	undefined
undefined	undefined	undefined

この真理値表から読み取れること:

• undefinedを含まない場合、A||BはA∨Bに等しい
• Aがtrueのとき、A||Bは常にtrue
• Aがfalseのとき、A||BはBに等しい
• Aがundefinedのとき、A||Bは常にundefined

よってif (A||B) {...}というプログラムは以下と同じということになる。

if (A) {
    ...
} else {
    if (B) {
        ...
    }
}

3値論理での否定（=!）

3値論理での否定は!で表す。例えばAの否定は$!A$となる。

• 真理値表

A	!A
true	false
false	true
undefined	undefined

*Aがundefinedなら!Aもundefined

3値論理でのドモルガンの法則の表を作る...

3値論理での論理積、論理和、否定を使って3値論理でのドモルガンの法則が適用できるのか表を使って調べてみることにする。

A	B	!A	!B	(!A)&&(!B)
T	T	F	F	F
T	F	F	T	F
T	U	F	U	F
F	T	T	F	F
F	F	T	T	T
F	U	T	U	U
U	T	U	F	U
U	F	U	T	U
U	U	U	U	U

(continued below)

(!A) ll (!B)	A&&B	!(A&&B)	A ll B	!(A ll B)
F	T	F	T	F
T	F	T	T	F
U	U	U	T	F
T	F	T	T	F
T	F	T	F	T
T	F	T	U	U
U	U	U	U	U
U	U	U	U	U
U	U	U	U	U

ドモルガンの法則を使ってif文を以下のように作り上げることができる。

if (!(x >= 0 && y >= 0)) {
    ...
}

　　　　↓

if (x < 0 || y < 0) {
    ...
}

まとめ

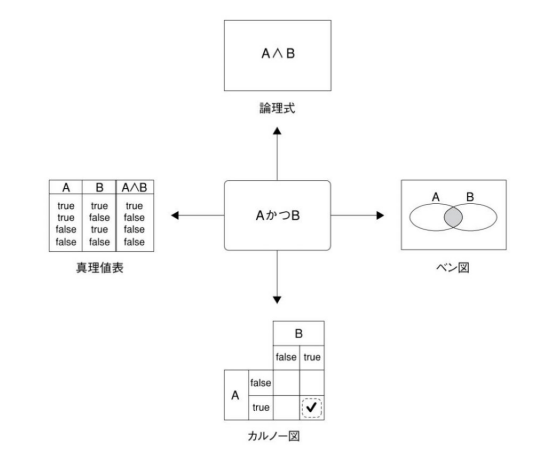
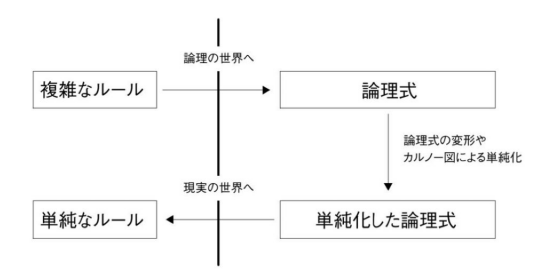
論理式、真理値表、ベン図、カルノー図などを使うことによって複雑な命題もシンプルな論理に変えることができる。（以下2つの画像は本書より転載）

疑問、思ったことなど

¬(A∧B) ≠ (¬A)∧(¬B)?

これは自分で勝手に証明してみただけなので本書に書いてあったわけではないが備忘録がてら書いてみることにする。この考えが正しい保証はありません。
まず$¬(A∧B)$だがこれをもとめるのには2つ方法がある。

1. $A∧B$の反転
   多分これが一番簡単な方法。A∧Bの真理値表の結果をそのまま反転させるだけ。

2. $¬A$と$¬B$に変換してからもとめる
   まず$¬A$と$¬B$の真理値表を作りそれにもとづいて$A∧B$を求める。しかしこのとき「AとBの両方がtrueのときだけtrueになる」とするのではなく「AとBの両方がfalseのときだけfalseになる」と考える。

2の方法でこれを「AとBの両方がtrueのときだけtrueになる」という法則に則って答えを出すと$(¬A)∧(¬B)$になると思われる。

A	B	¬A	¬B	(A∧B)	¬(A∧B)	(¬A)∧(¬B)
true	true	false	false	true	false	false
true	false	false	true	false	true	false
false	true	true	false	false	true	false
false	false	true	true	false	true	true

¬(A∨B) ≠ (¬A)∨(¬B)?

実際にやってみたのだが全く同じことがこちらでも言える。1と2のステップを$∨$に変えて以下の表を作ってみた。先程と同様、(¬A)∨(¬B) に関しては「AとBの少なくともどちらか片方がtrueのときにtrue」を「AとBの少なくともどちらか片方がfalseのときにfalse」と書き換えると(¬A∨¬B)と同じ結果を得られる。

が、これを「AとBの少なくともどちらか片方がtrueのときにtrue」に則って考えると以下のようになる。

A	B	¬A	¬B	(A∨B)	¬(A∨B)	(¬A)∨(¬B)
true	true	false	false	true	false	false
true	false	false	true	true	false	true
false	true	true	false	true	false	true
false	false	true	true	false	true	true

もし$¬(A∨B) = (¬A)∨(¬B)$と$¬(A∧B) = (¬A)∧(¬B)$が真であると証明されたとしたら上の2つのひょうの中の一番右の列2つがその左隣りの値とおなじになるはずだ。