Matlabを使った振動制御のシミュレーション

産業機械を動かす際に生じる機械振動を抑えるための制御手法をMATLABを使ってシミュレーションします。下図のような位置制御されたモータとモータに取り付けられた共振系からなるシステムを考えます。今回は，共振が主共振と奇数倍の高調波からなる連生振動系を扱います。

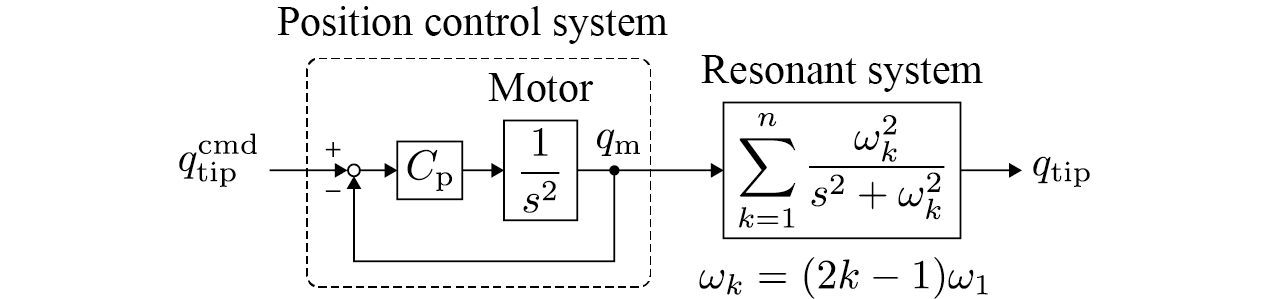
ここで，$q$は一般化位置を示し,$q_{\rm tip}$は先端位置，$q_{\rm m}$はモータ位置，$q_{\rm tip}^{\rm cmd}$は先端位置指令とします。$C_{\rm p}$は位置制御器を表し，共振系の主共振を$\omega_1$ [rad/s]であるとします。この制御系に，下図のような$T_{\rm w}$秒の時間遅れとゲイン$m$を用いた先端位置フィードバックと入力整形ゲイン$1-m$を導入します。

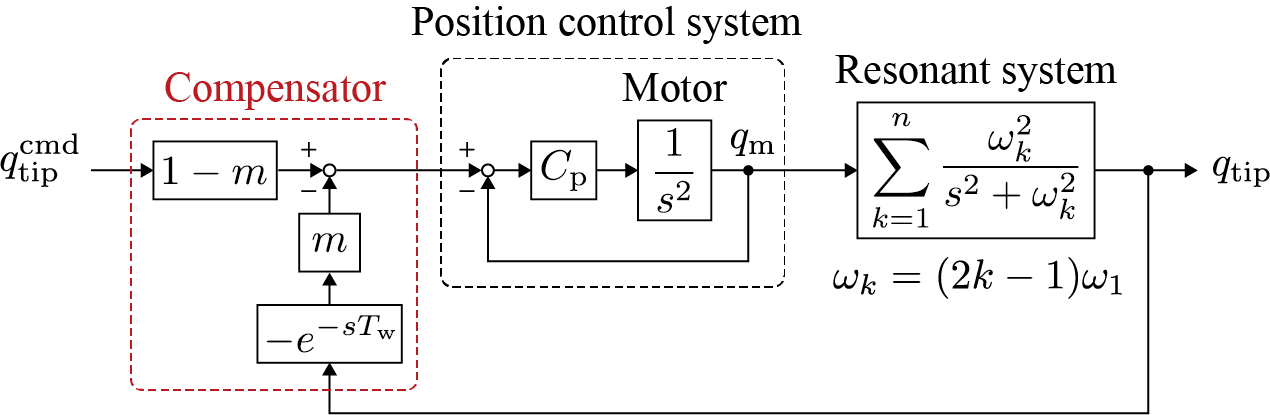
ここで，時間遅れ量は$T_{\rm w}=\pi/2\omega_1$と決定されるものとします。この単純な制御系によって振動が抑制されます。

vib.m

clear;         

s=tf('s');
t_range=0.5;

%Plant parameter
f_std=12.3456789;
w_std=2.0*pi*f_std;

%Compensator
Td=1.0/(4*f_std);
d=-exp(-s*Td);
m=0.6;

%Motor
Kp=22500.0;
Kd=4.0*sqrt(Kp);
Cp=Kp+Kd*s;
Gm=Cp/(s^2+Cp);

%Plant
plant=1;
NumOfHarmonics=25;

for n=1:1:NumOfHarmonics
    w=w_std*(2*n-1);
    plant=plant*w^2/(s^2+w^2);
end

%System
sys=Gm*plant;

%Closed loop
sys_closed=(1-m)*(sys/(1+sys*m*d));

step(sys,sys_closed,t_range);

NumOfHarmonicsで共振の個数を設定しています。Matlabの数値計算誤差の影響で制御出力が発散しない限り，どんな値でも振動が止まります。応答結果の一例を以下に示します。

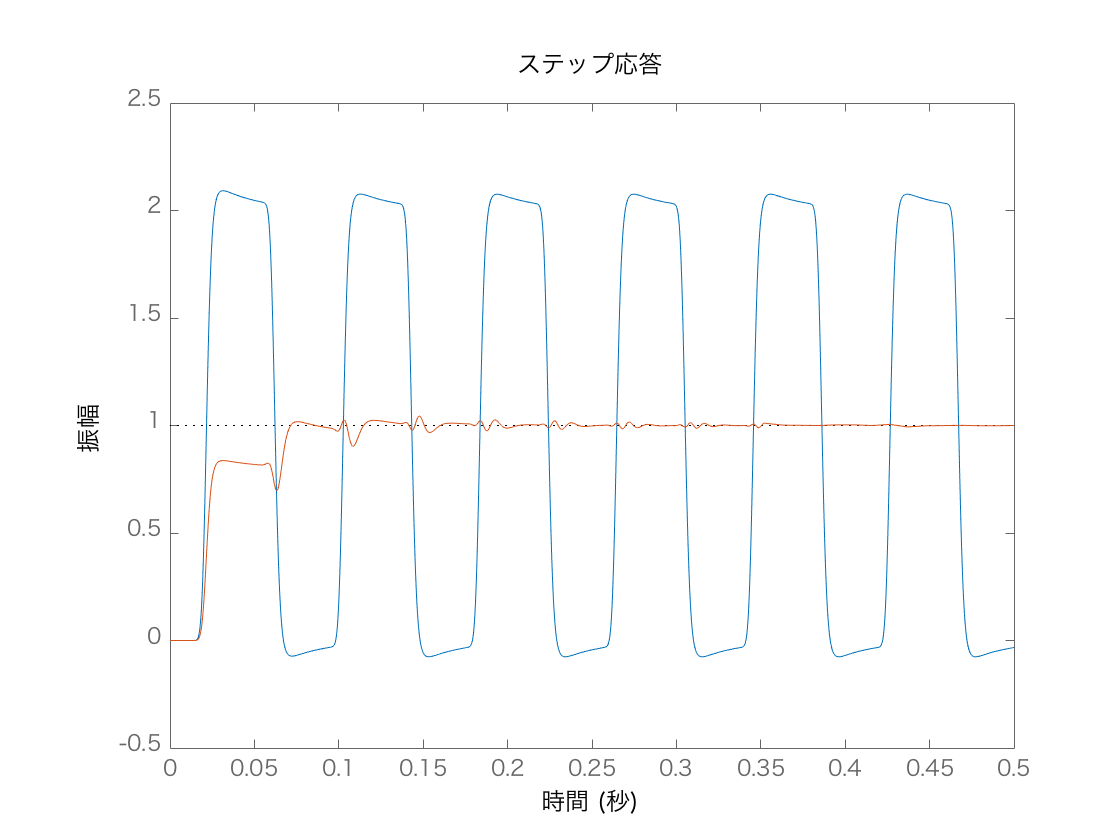
設計パラメータ$m$を大きくすると応答が遅くなり，オーバーシュートが消えます。微分演算など面倒なことが必要ないので，簡単に使えます。

設計が面倒な時のための自動調整
https://qiita.com/wcrvt/items/59bedde75ac0d6bf7ea1