概要
なかなか手が出なかったRecurrent Neural Network(RNN)のお勉強を始めていきたいと思います。基本はLSTMを使った再帰的な処理を用いて予測を行なっていくような形ですが、なにぶんまだ写経に近いところもあり、完全に理解できているわけではないので間違い等があればご指摘いただきたく。
参考にした先
RNN + LSTMのChainerでの実装例はChainerのサンプルを参考にしました。
ただ、このままだと今まで自分で作ってきたフレームワークにはまらないので、少々加工を行いました。上記のコードの解説はここが詳しいかったです。
あとは最近でた本でざっくりとRNNとLSTMについて理解しています。
問題設定
サンプルそのままを動かしてもなんだか面白くないので、問題設定をしてみます。
実務でも従前から言われるのですが、ExcelのRand()関数で作る乱数の周期は$2^{24}$であり、他の乱数に比べて周期が短いことが知られています。そのため、モンテカルロなんかでExcelの乱数を使うと結果に偏りが出たりします。(まぁ少ないサンプル数の場合はいいのかもしれません)
一方、Rの乱数はメルセンヌ・ツイスタというアルゴリズムで作られる非常に長い周期($2^{19937}$)を持つ乱数になっています。
つまり、周期性が存在するのであればRNNを使った逐次学習を行うことで、次に出る乱数値が予測できるのではないか?というのが問題意識です。
乱数の専門家ではないので、評価方法が正しいかどうかは不明。
データの用意
まずExcelの乱数は、Rand関数を使って、
=ROUNDDOWN(RAND()*10,0)
としたものを1001個用意します。すると、0-9までの10個の整数値が得られます。
次にRの乱数は一様乱数を以下のように生成します。
x <- floor(runif(1001)*10);
(1001になっているのは、答えデータを次の値にするために1個余分に作っています。)
説明変数は現時点の乱数値(0-9)とし、教師データを次の乱数値(0-9)とします。
RNNの実装
RNNはChainerを用いて以下のように実装しました。
逐次処理なので、意図的にバッチサイズを1として最初から順番に一個づつ処理していくようにしています。
まずベースクラスが以下のようになっています。
# -*- coding: utf-8 -*-
from chainer import FunctionSet, Variable, optimizers,serializers
from chainer import functions as F
from chainer import links as L
from sklearn import base
from sklearn.cross_validation import train_test_split
from abc import ABCMeta, abstractmethod
import numpy as np
import six
import math
import cPickle as pickle
class BaseChainerEstimator(base.BaseEstimator):
__metaclass__= ABCMeta # python 2.x
def __init__(self, optimizer=optimizers.MomentumSGD(lr=0.01), n_iter=10000, eps=1e-5, report=100,
**params):
self.report = report
self.n_iter = n_iter
self.batch_size = params["batch_size"] if params.has_key("batch_size") else 100
self.network = self._setup_network(**params)
self.decay = 1.
self.optimizer = optimizer
self.optimizer.setup(self.network.collect_parameters())
self.eps = eps
np.random.seed(123)
@abstractmethod
def _setup_network(self, **params):
return FunctionSet(l1=F.Linear(1, 1))
@abstractmethod
def forward(self, x,train=True,state=None):
y = self.network.l1(x)
return y
@abstractmethod
def loss_func(self, y, t):
return F.mean_squared_error(y, t)
@abstractmethod
def output_func(self, h):
return F.identity(h)
@abstractmethod
def fit(self, x_data, y_data):
batchsize = self.batch_size
N = len(y_data)
for loop in range(self.n_iter):
perm = np.random.permutation(N)
sum_accuracy = 0
sum_loss = 0
for i in six.moves.range(0, N, batchsize):
x_batch = x_data[perm[i:i + batchsize]]
y_batch = y_data[perm[i:i + batchsize]]
x = Variable(x_batch)
y = Variable(y_batch)
self.optimizer.zero_grads()
yp = self.forward(x)
loss = self.loss_func(yp,y)
loss.backward()
self.optimizer.update()
sum_loss += loss.data * len(y_batch)
sum_accuracy += F.accuracy(yp,y).data * len(y_batch)
if self.report > 0 and (loop + 1) % self.report == 0:
print('loop={:d}, train mean loss={:.6f} , train mean accuracy={:.6f}'.format(loop + 1, sum_loss / N,sum_accuracy / N))
self.optimizer.lr *= self.decay
return self
def predict(self, x_data):
x = Variable(x_data,volatile=True)
y = self.forward(x,train=False)
return self.output_func(y).data
def predict_proba(self, x_data):
x = Variable(x_data,volatile=True)
y = self.forward(x,train=False)
return self.output_func(y).data
def save_model(self,name):
with open(name,"wb") as o:
pickle.dump(self,o)
class ChainerClassifier(BaseChainerEstimator, base.ClassifierMixin):
def predict(self, x_data):
return BaseChainerEstimator.predict(self, x_data).argmax(1)
def predict_proba(self,x_data):
return BaseChainerEstimator.predict_proba(self, x_data)
次のRNNの実装は以下のようになっています。
class RNNTS(ChainerClassifier):
"""
Recurrent Neurarl Network with LSTM by 1 step
"""
def _setup_network(self, **params):
self.input_dim = params["input_dim"]
self.hidden_dim = params["hidden_dim"]
self.n_classes = params["n_classes"]
self.optsize = params["optsize"] if params.has_key("optsize") else 30
self.batch_size = 1
self.dropout_ratio = params["dropout_ratio"] if params.has_key("dropout_ratio") else 0.5
network = FunctionSet(
l0 = L.Linear(self.input_dim, self.hidden_dim),
l1_x = L.Linear(self.hidden_dim, 4*self.hidden_dim),
l1_h = L.Linear(self.hidden_dim, 4*self.hidden_dim),
l2_h = L.Linear(self.hidden_dim, 4*self.hidden_dim),
l2_x = L.Linear(self.hidden_dim, 4*self.hidden_dim),
l3 = L.Linear(self.hidden_dim, self.n_classes),
)
return network
def forward(self, x, train=True,state=None):
if state is None:
state = self.make_initial_state(train)
h0 = self.network.l0(x)
h1_in = self.network.l1_x(F.dropout(h0, ratio=self.dropout_ratio, train=train)) + self.network.l1_h(state['h1'])
c1, h1 = F.lstm(state['c1'], h1_in)
h2_in = self.network.l2_x(F.dropout(h1, ratio=self.dropout_ratio, train=train)) + self.network.l2_h(state['h2'])
c2, h2 = F.lstm(state['c2'], h2_in)
y = self.network.l3(F.dropout(h2, ratio=self.dropout_ratio, train=train))
state = {'c1': c1, 'h1': h1, 'c2': c2, 'h2': h2}
return y,state
def make_initial_state(self,train=True):
return {name: Variable(np.zeros((self.batch_size, self.hidden_dim), dtype=np.float32),
volatile=not train)
for name in ('c1', 'h1', 'c2', 'h2')}
def fit(self, x_data, y_data):
batchsize = self.batch_size
N = len(y_data)
for loop in range(self.n_iter):
sum_accuracy = Variable(np.zeros((), dtype=np.float32))
sum_loss = Variable(np.zeros((), dtype=np.float32))
state = self.make_initial_state(train=True) #initial stateの生成
for i in six.moves.range(0, N, batchsize):
x_batch = x_data[i:i + batchsize]
y_batch = y_data[i:i + batchsize]
x = Variable(x_batch,volatile=False)
y = Variable(y_batch,volatile=False)
yp,state = self.forward(x,train=True,state=state)
loss = self.loss_func(yp,y)
accuracy = F.accuracy(yp,y)
sum_loss += loss
sum_accuracy += accuracy
if (i + 1) % self.optsize == 0:
self.optimizer.zero_grads()
sum_loss.backward()
sum_loss.unchain_backward()
self.optimizer.clip_grads(5)
self.optimizer.update()
if self.report > 0 and (loop + 1) % self.report == 0:
print('loop={:d}, train mean loss={:.6f} , train mean accuracy={:.6f}'.format(loop + 1, sum_loss.data / N,sum_accuracy.data / N))
self.optimizer.lr *= self.decay
return self
def output_func(self, h):
return F.softmax(h)
def loss_func(self, y, t):
return F.softmax_cross_entropy(y, t)
def predict_proba(self, x_data):
N = len(x_data)
state = self.make_initial_state(train=False)
y_list = []
for i in six.moves.range(0, N, self.batch_size):
x = Variable(x_data[i:i+self.batch_size],volatile=True)
y,state = self.forward(x,train=False,state=state)
y_list.append(y.data[0]) #batch size = 1のみに対応
y = Variable(np.array(y_list),volatile=False)
return self.output_func(y).data
def predict(self, x_data):
return self.predict_proba(x_data).argmax(1)
ほぼほぼ参照したコードを採用しています。
ここまで書いてしまうとメイン処理は単純に書けて、
# -*- coding: utf-8 -*-
import pandas as pd
import numpy as np
from DL_chainer import *
import warnings
from sklearn.metrics import classification_report
warnings.filterwarnings("ignore")
I_FILE_EXCEL="excelrand.csv"
I_FILE_R="RRandom.csv"
def main(file=""):
"""
Excelの乱数をRNNで学習して予測する
:return:
"""
df0 = pd.read_csv(file)
N = len(df0)
x_all = df0.iloc[:,0]
y_all = []
y_all.extend(x_all)
y_all.extend([np.nan])
y_all = y_all[1:(N+1)]
x_all_array = np.reshape(np.array(x_all[0:(N-1)],dtype=np.float32),(len(x_all)-1,1))/10
y_all_array = np.reshape(np.array(y_all[0:(N-1)],dtype=np.int32),(len(x_all)-1))
train_n = 2 * N/3
x_train = x_all_array[0:train_n]
y_train = y_all_array[0:train_n]
x_test = x_all_array[train_n:]
y_test = y_all_array[train_n:]
params = {"input_dim":1,"hidden_dim":100,"n_classes":10,"dropout_ratio":0.5,"optsize":30}
print params
print len(x_train),len(x_test)
rnn = RNNTS(n_iter=200,report=1,**params)
rnn.fit(x_train,y_train)
pred = rnn.predict(x_train)
print classification_report(y_train,pred)
pred = rnn.predict(x_test)
print classification_report(y_test,pred)
if __name__ == '__main__':
main(I_FILE_R)
main(I_FILE_EXCEL)
基本は10クラス分類問題になります。
結果の評価
結果の評価は難しいところです。
少ないサンプル数のテストデータでは正しい評価ができないと考えられます。
どちらの乱数列を使っても基本的にはRNNの学習は進みます。そこで、同一エポック数でどのようの学習速度が違うか、をみることにしました。
つまり、同一エポックにおいて、より精度が出ている方は、データ内になんらかのパターンがあり、それを学習「されて」しまっている、と解釈します。
乱数としてはパターンの存在はない方がいいので、この学習速度が遅い方が当然いい、というわけです。
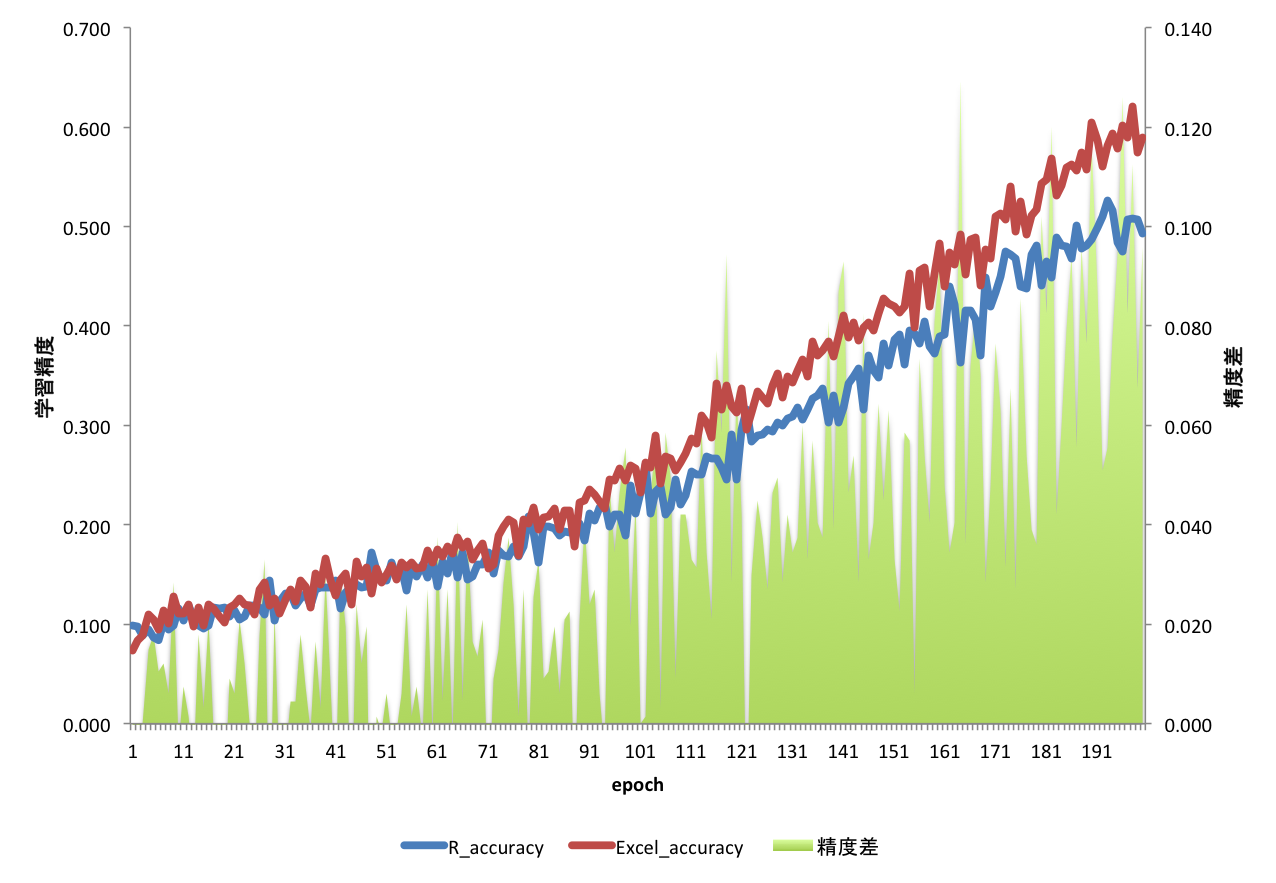
結果が以下、
Excel側の方がRよりも学習速度が速いことがわかります。
つまり、乱数の質的にはRの方が良いと見れるかな。本当は学習が進まない方がいいのだけど。
まとめ
今回はRNNの練習のために、実装を試しに行ってみてExcelとRの乱数の学習を行いました。結果の評価方法が正しいかどうかは別にして、この評価方法だとExcel側の学習が速く進み、乱数としてはRの方が質がいいということがわかりました。
たぶん、もっとちゃんと検証するには無数の乱数列が必要なのですが、計算機パワーの関係でこのくらいにしておきました。
にしても、RNNで計算速度を上げるにはどうしたらいいのだろう・・・