動的線型モデルの使い方(とりあえず動かしてみる編)

========================================================
DLM(動的線型モデル)を用いて、Nileデータを観測値とした、状態の推定を行う。

参考書はこちら。

rm(list = ls(all = T))
library(dlm)

## Warning: package 'dlm' was built under R version 3.0.3

data.vec <- Nile

Nileデータの中身は以下のよう。

head(data.vec)

## [1] 1120 1160  963 1210 1160 1160

モデルの生成

ローカルレベルモデルを構築する。ここで、$V$,$W$は既知の分散共分散行列、$F=1$、$G=1$としている。

$Y_t = F\theta_t + N(0,V)$

$\theta_t = G\theta_{t-1} + N(0,W)$

dlmPoly <- dlmModPoly(order = 1, dV = 1e+05, dW = 5000)
dlmPoly

## $FF
##      [,1]
## [1,]    1
## 
## $V
##       [,1]
## [1,] 1e+05
## 
## $GG
##      [,1]
## [1,]    1
## 
## $W
##      [,1]
## [1,] 5000
## 
## $m0
## [1] 0
## 
## $C0
##       [,1]
## [1,] 1e+07

フィルタリング分布の推定

以下の流れでカルマンフィルタを実行し、状態のフィルタリング分布を推定する。
動的線型モデルでは、すべてガウス分布となるため、平均と分散を求めれば十分である。

状態一期先予測

$a_t = E(\theta_t|y_{1:t-1})=G_tm_{t-1}$

$R_t = Var(\theta_t|y_{1:t-1})=G_tC_{t-1}G_t^T+W_t$

観測値一期先予測

$f_t = E(Y_t|y_{1:t-1})=Fa_t$

$Q_t = Var(Y_t|y_{1:t-1})=F_tR_tF_t^T+V_t$

状態フィルタリング

$m_t = E(\theta_t|y_{1:t})=a_t + R_tF_t^TQ_t^{-1}(Y_t-F_ta_t)$

$C_t = Var(\theta_t|y_{1:t})=R_t - R_tF_t^TQ_t^{-1}F_tR_t$

dataFilt <- dlmFilter(data.vec, dlmPoly)

フィルタリング分布の平均値

head(dropFirst(dataFilt$m), 10)

##  [1] 1109 1135 1073 1113 1125 1133 1062 1098 1155 1152

平滑化分布の推定

任意のt<Tにおいて、$y_{1:T}$が与えられた下での$\theta_t$の条件付き分布を計算する。

平滑化分布

$s_t = E(\theta_t|y_{1:T}) = m_t + C_tG_{t+1}^TR_{t+1}^{-1}(s_{t+1}-a_{t+1})$

$S_t = E(\theta_t|y_{1:T}) = C_t - C_tG_{t+1}^TR_{t+1}^{-1}(R_{t+1}-S_{t+1})R_{t+1}^{-1}G_{t+1}C_t0$

dataSmth <- dlmSmooth(dataFilt)

平滑化分布の平均値

head(dropFirst(dataSmth$s), 10)

##  [1] 1106 1105 1102 1107 1105 1102 1095 1102 1103 1091

プロット

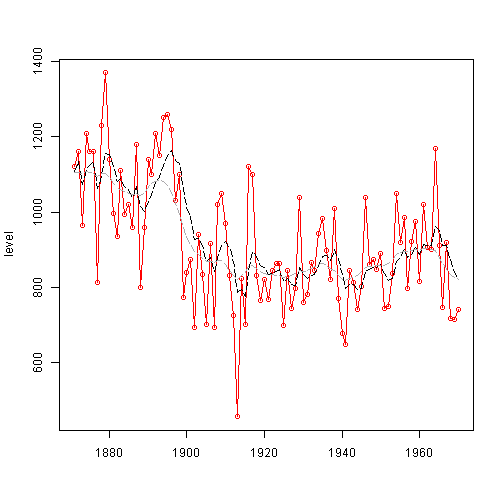
観測値、フィルタリング分布平均値、平滑化分布平均値の推移。
フィルタリングでは、観測値のピークと1期分ずれて推定されているようである。

plot(data.vec, type = "o", col = c("red"), xlab = "", ylab = "level")
lines(dropFirst(dataFilt$m), lty = "longdash")
lines(dropFirst(dataSmth$s), lty = "longdash", col = c("darkgrey"))

信号雑音比の違いによる変化

信号雑音非$W/V$は事前状態から事後状態への更新が予想外の観測値に対してどの低程度敏感であるかを決める。
そこで、信号雑音比が異なる二つのモデルのフィルタリング分布を比べる。

一つ目は$V=14000,W=700,W/V=0.05$のモデル。

dlmPoly2 <- dlmModPoly(order = 1, dV = 14000, dW = 700)
# dlmPoly2;
dataFilt2 <- dlmFilter(data.vec, dlmPoly2)

二つ目は$V=14000,W=7000,W/V=0.5$のモデル。

dlmPoly3 <- dlmModPoly(order = 1, dV = 14000, dW = 7000)
# dlmPoly3;
dataFilt3 <- dlmFilter(data.vec, dlmPoly3)

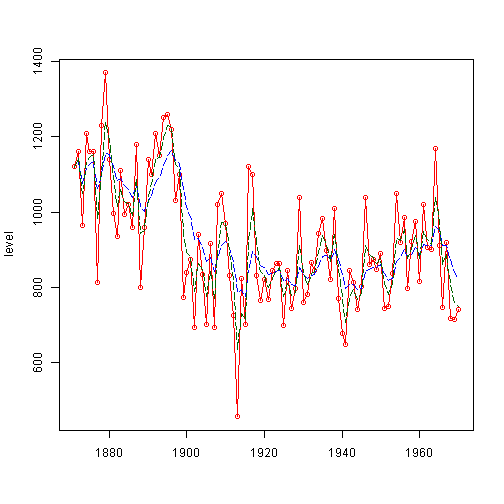
信号雑音比が大きいほど、観測値により近いフィルタリング分布になる。
信号雑音比$W/V$が大きいということは$V$が小さいということであり、観測誤差が小さくなる。そのため、データを信頼する方向へと動く。

plot(data.vec, type = "o", col = c("red"), xlab = "", ylab = "level")
lines(dropFirst(dataFilt2$m), lty = "longdash", col = c("blue"))
lines(dropFirst(dataFilt3$m), lty = "longdash", col = c("darkgreen"))