はじめに
前回の記事ではバリオグラムによる理論バリオグラムの設定と共分散関数を求めました。
今回はいよいよクリギングによる補完をしていきたいと思います。
使用するデータ
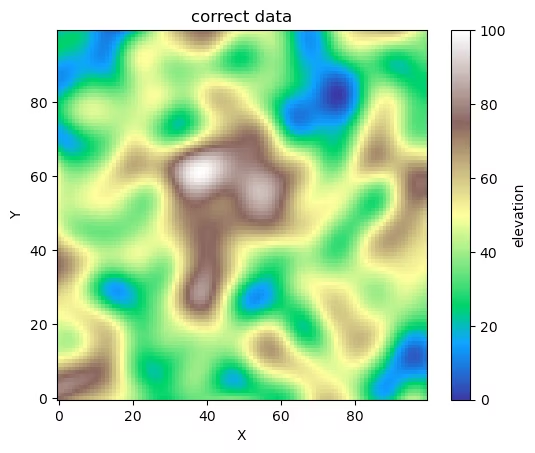
使用するデータは前回同様、ChatGPTに作成させた標高データを用います。
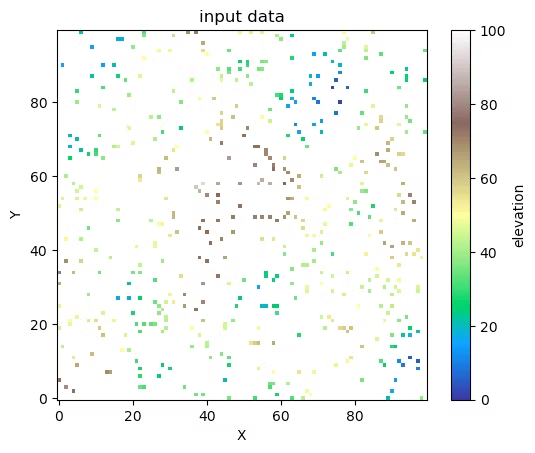
そしてこのデータから500点をサンプリングしたものを入力データとします。
前回は、このサンプリングデータから共分散関数を求めました。
C(h)=325.2\bigg[\exp\bigg\{-\bigg(\frac{h}{12.6}\bigg)^2\bigg\}\bigg]
この共分散関数を用いて単純クリギングをしていきたいと思います。
単純クリギング
単純クリギングは、全体の期待値が既知である時に用いることができる手法です。推定箇所の目的変数を求める式は以下の線形和になります。
z_0=m+\sum^n_{k=1}\omega_k(z_k-m)
ここで、$z_0$は求めたい箇所の目的変数、$z_1,z_2,...,z_n$はサンプルデータの目的変数、$\omega$はパラメータ、$m$は期待値です。この時のパラメータは以下の式で決定します。
\left[\begin{array}{cccc}\omega_1\\
\omega_2\\
\vdots\\
\omega_n
\end{array}
\right]=\left[\begin{array}{cccc}
C(0)&C(h_{1,2})&\ldots&C(h_{1,n})\\
C(h_{2,1})&C(0)&\ldots&C(h_{2,n})\\
\vdots&\vdots&\ddots&\vdots\\
C(h_{n,1})&C(h_{n,2})&\ldots&C(0)
\end{array}
\right]^{-1}
\left[\begin{array}{cccc}C(h_{0,1})\\
C(h_{0,2})\\
\vdots\\
C(h_{0,n})
\end{array}
\right]
$h_{i,j}$は、目的変数$z_i$、$z_j$間のユークリッド距離です。そして、クリギングは推定誤差分散も求めることができます。
{\sigma_0}^2=C(0)-\sum_{k=1}^{n}\omega_kC(h_{0,k})
今回、標本平均は母平均と等しいものとして$m$を求め、$m$=45.0となりました。入力行列の欠損箇所を逐次$z_0$として単純クリギングを行いました。
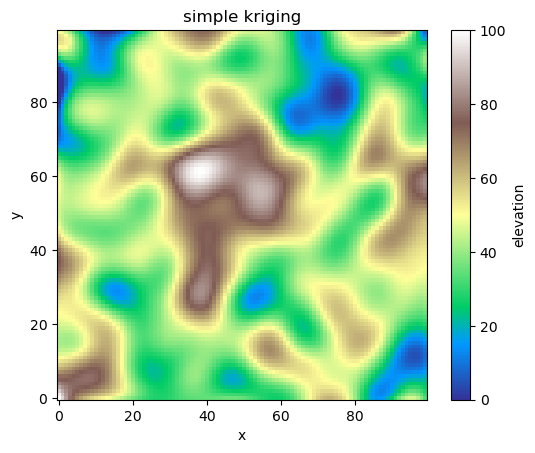
まず、標高の推定結果です。
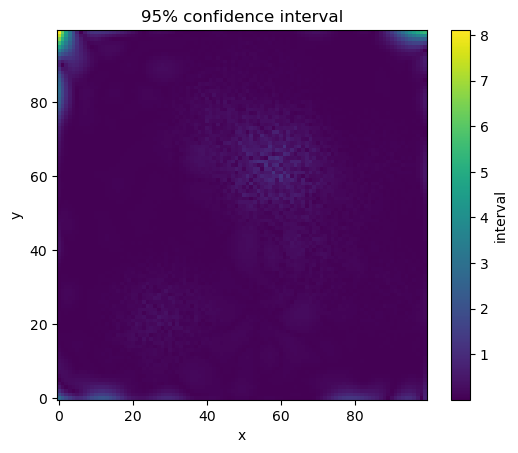
続いてこちらが95%信頼区間で起こりうる誤差分布です。
この結果から、角に高い分散が集中していることがわかりました。
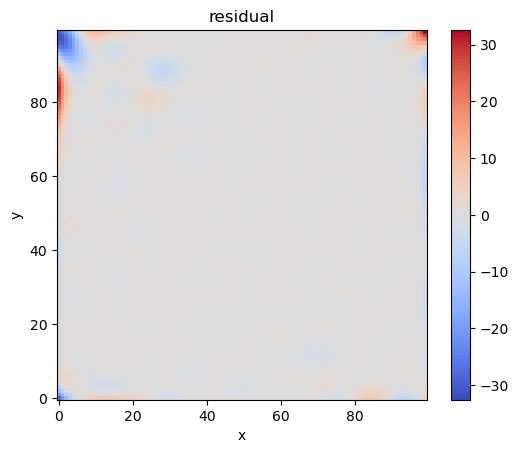
正解値と単純クリギング結果の残差分布を確認してみます。
分布傾向は合っていそうですが、小さい分散を出力していると感じました。
さいごに
今回は単純クリギングのやり方と推定結果の考察まで紹介しました。分散が小さく出力される原因としては、理論バリオグラムを選定せず、ガウスモデルを無理やり使用したためかな、と考えます。意外と理論バリオグラムの選定、大事そうですね。次回は通常クリギングについて書きたいと思います。
参考文献
コロナ社:阪田義隆「クリギング入門」